三角函数的傅立叶变换推导公式

(大连理工大学 辽宁 大连 116023)

一、狄利克雷条件

设f(x)是以2l为周期并且定义在[-l,l]上可积。可以知道下列傅立叶级数的展开式：

(1)

然而想取等号时，需要公式(1)收敛，并且收敛于f(x)是需要条件的。其中最常见的是满足狄利克雷条件。当f(x)满足狄利克雷条件时，f(x)可以取等号，下列给出狄利克雷条件—函数f(x)在区间[-l,l]上满足:

(1)连续，或只有有限个间断点，且都是第一类间断点；

(2)只有有限个极值点。

(2)

当函数满足狄利克雷条件时，第一行为x∈(-l,l)在f(x)的连续点，第二行为x∈(-l,l)在f(x)的第一类间断点，第三行为x=±l函数的端点值。

二、三角函数的傅立叶变换

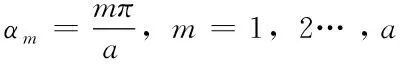
由于上述公式为非周期函数且取值范围在[0,a]。根据上述傅立叶级数的描述情况，sin(αmx)满足狄利克雷条件，所以我们把此三角函数进行偶延拓，再进行周期延拓，然后利用傅立叶级数进行表达：

(3)

当m=p时，可以得到ap=0，所以下列为m≠p时：

将此过程置换顺序之后，同理可得：

当p=0时：

根据上述得到的结论，可以把此三角函数写成：

(4)

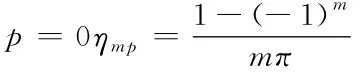
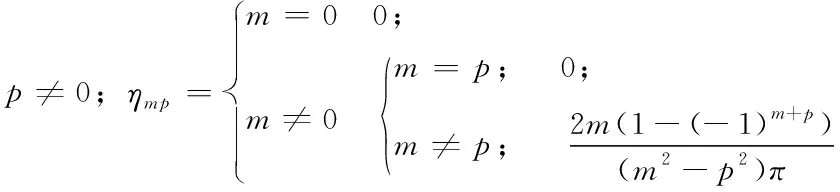
同样，对于cos(αmx)也可以做上述推导，可以由读者自行推导，验证。本文简单地介绍了傅立叶级数的使用和拓展，在纯数学推导中研究傅立叶函数的应用。在我们无法进行理论证明的时候，采用直观推断的研究方法其实在早期的科学研究中，已经被广泛地应用，因此也带来了很多的重要发现，傅立叶级数就是其中之一。