融合有限差分及梯度的Bayer-CFA插值方法

贾晓芬,郭永存,赵佰亭,黄友锐

(安徽理工大学智能矿山技术与装备工程省重点实验室,232001,安徽淮南)

在当今的数字信息时代,数码相机的使用非常普及,为了缩小体积、降低成本,多数设备中仅有一个传感器并覆盖彩色滤波阵列(color filter array,CFA)。采用此结构的成像设备在每个像素点只能采集到一个颜色(红、绿或者蓝),其余两个颜色需要估计,估计的过程被称为CFA插值或去马赛克。针对广泛使用的CFA模式[1],大量致力于消除伪彩色、边缘模糊、锯齿现象的方法[2-4]相继提出。

彩色图像的邻域像素之间具有较强的空间相关性,各通道间还存在强烈的色彩(光谱)相关性,充分利用图像相关性才能获得高质量的CFA插值效果。文献[5-6]提出了基于颜色比的插值方法,文献[7-8]提出了基于颜色差值的插值方法,均考虑了图像相关性。结合了图像相关性的先进技术能进一步提高插值精度,例如:黄丽丽等利用稀疏表示实现了CFA插值[9];Jia等利用支持向量机获得了高质量的CFA插值图像[10-11]。近年来,各种利用图像梯度信息的方法取得了较好的插值效果[12-14],例如:Wu等利用多项式插值实现了CFA插值[4];Jain等将偏微分方程和有限差分法引入到了图像处理中[15-16];Yang等利用有限差分实现图像平稳过渡,从而完成了图像拼接[17]。

图像梯度的大小和方向体现边缘信息,准确利用梯度不仅可以提高插值精度,还可以保护图像的边缘。将CFA图像中的已知像素点作为离散的网格节点,利用像素间的空间相关性设计插值函数,可以实现有限差分对连续像素值的逼近,完成对丢失像素值的估计。研究梯度、有限差分及图像相关性相结合的CFA插值方法是有意义的,鉴于此,本文设计了一种融合上述技术的称为Bayer-CFA的插值方法。

1 理论基础

有限差分法又称网格法,是最早用计算机进行数值模拟的方法[18]。它将连续的定解区域划分为差分网格,利用有限网格节点代替连续的求解区域,利用差商代替微分方程中的偏导数,得到相应的差分方程,再利用插值方法解差分方程,就可以得到原问题在离散点上的近似解。在数字图像处理中,可以通过计算插值函数来逼近连续像素值。将有限差分用于图像CFA插值时,可以把已知的像素值作为被称之为网格节点的离散点,再用离散点插值估计出未知的像素值,即可得到图像的连续像素值。

数字图像实质上是二维离散函数,函数的导数就是图像梯度,一般用差分近似表示。图像梯度在图像的每个像素点都是一个具有大小和方向的矢量,含有边缘信息,边缘处的梯度值较大,梯度的方向代表函数变化最快的方向。沿着边缘方向插值能够减少锯齿现象。因此,CFA插值时利用梯度信息构造插值及修正的权重因子能提高插值精度。

CFA插值时,充分利用图像的相关性是获得高质量彩色图像的保障。彩色图像除了每个颜色平面上像素间具有空间相关性,各颜色平面之间还具有强烈的色彩相关性,并满足色差恒定定理[7-8],即在局部区域内的色差值是常数。若K为色差值,则KR=IG-IR表示G(绿)平面和R(红)平面对应像素之间的色差值,KB=IG-IB表示G平面和B(蓝)平面对应像素之间的色差值,IR、IG、IB分别表示R、G、B平面的像素值,插值过程需要充分利用该特性。为有效结合有限差分、梯度及相关性,实现高精度CFA插值,本文设计了如图1所示的插值流程。

图1 CFA插值流程

首先结合空间相关性,用插值多项式的插值误差构造插值函数,结合色差理论获取插值算子,利用5×5邻域内的梯度构造估计中心像素值的权重因子,完成G平面插值。然后用已知R像素点的对称性调整插值函数,结合色彩相关性构建G和B像素点的插值函数,实现R平面插值。再用和R平面相同的方法实现B平面插值。完成插值后,在以插值点为中心的3×3邻域内用梯度信息构造8个方向的权重因子,采用空间距离决定权重因子的加权系数实现梯度修正。

2 Bayer-CFA插值方法

2.1 构造插值函数

(1)

式中min{xi}≤ξ≤max{xi}。

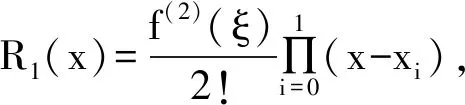
f(x)≈f(x0)+f′(x0)(x-x0)+R1(x)

(2)

由有限差分方程可得

(3)

取x=x0+h/2,将式(3)代入式(2)可得

(4)

CFA图像中的像素间隔为整数倍像素,为了将式(4)作为CFA图像的插值函数,h的取值必须是偶数。图像像素之间的距离越近,则空间相关性越强,反之则越弱。为了保证插值函数充分利用图像的空间相关性,取h=2。此时,M项由2个依次相距2像素的点构成,N项由3个依次相距2像素的点构成。

2.2 插值G平面

(5)

(6)

(7)

将式(6)(7)代入式(5)可得

(8)

(9)

图像的梯度包含边缘信息,利用梯度信息实现插值有助于提高插值精度。为了获得准确的梯度信息,在5×5邻域内用待插值点的多个已知相邻像素点计算梯度,利用梯度信息构造梯度算子,公式为

(10)

(11)

由式(10)(11)得到权重因子ωH=1/H、ωV=1/V,最终获得B点的G像素估计值为

(12)

在R点插值G像素的方法同上,只需将式(5)～(11)中的B换成R即可。

G平面插值完成后,平面上的所有像素点均为已知。下面利用色差值和G平面上所有的已知像素值插值估计其余两个平面。

2.3 插值R平面

在Bayer型CFA图像中,G像素点有两种位置:(1)只有G和R像素点的行,后文记为GR行;(2)只有G和B像素点的行,后文记为GB行。

2.3.1 G平面插值R像素 GR行的G点左右均为已知的R像素点,因此在G点的水平方向估算G点的色差,公式为

(13)

式中第一项对应式(4)的M项,第二项对应式(4)的N项。M项由G点左右相邻的2个R点的色差值构成。N项由3个依次相距2像素的R点的色差值构成。

同理,GB行的G点上下均为已知的R像素点,在G点的垂直方向估算G点的色差值,公式为

(14)

图2 B平面插值R像素的3×3邻域

(15)

2.4 插值B平面

图3 R平面插值B像素的3×3邻域

3 梯度修正插值精度

不规则边缘及纹理的存在,会使邻域内的像素值发生突变,导致空间相关性减小,引起插值误差。为了有效减小插值误差,根据不同插值方向的相邻像素间的空间相关性的差异来分配不同的插值权重,用来修正插值结果,从而达到提高插值精度的目的。

3.1 修正邻域

(a) B点或R点估计的空间位置 (b) B点估计的空间位置 (c) G点估计的空间位置图4 插值点的空间位置

3.2 修正过程

在3×3邻域内对插值结果进行修正的过程分为三步,具体步骤如下。

第一步,计算中心像素点与其8邻域的像素差值,即中心点在8个方向的梯度值,公式为

1=|Xi,j-Xi,j+1|;2=|Xi,j-Xi,j-1|;

3=|Xi,j-Xi+1,j|;4=|Xi,j-Xi-1,j|;

5=|Xi,j-Xi-1,j-1|;6=|Xi,j-Xi-1,j+1|;

7=|Xi,j-Xi+1,j-1|;8=|Xi,j-Xi+1,j+1|

(16)

式中X=R,G,B。

第二步,计算权重因子,公式为

ωm=1/m,m=1,2,…,8

(17)

3.3 修正结果

G像素值:如图4a所示,水平垂直四邻域均为已知G像素值,对角四邻域均为估计出的G像素值,为了提高修正精度,采用欧式距离决定加权系数,修正结果为

(18)

式中k1和k2分别是第2.2节获得的G像素估计值及本节修正项的权重,满足k1+k2=1,且k1>0.5,k2<0.5。

R像素值:如图4b所示,对角四邻域均为已知的R像素值,为充分利用已知像素值及邻域像素间的空间相关性提高修正精度,采用棋盘距离决定加权系数,修正结果为

(19)

式中v1和v2分别是2.3节获得的R像素估计值及本节修正项的权重,满足v1+v2=1,且v1>0.5,v2<0.5。

R像素值:如图4c所示,GB行的G点上下是已知的R像素值,GR行的G点左右是已知的R像素值,其余6个像素点的R像素值均为估计值,增大2个已知R像素值的权重,GR行的G点的R像素值为

(20)

GB行的G点的R像素值为

(21)

B像素值的修正方法和R像素值的类似,不再赘述。按照上述方法,首先在第2节得到各像素点的估计值,再用第3节得到的修正值去替代,即可得到最终的彩色图像,完成CFA插值。

4 仿真实验

采用MatlabR2016a编程,在3.60GHz的Intel(R)Core(TM)i7-7700CPU、16.0GB内存的台式机上运行本文程序。采用24幅分辨率为768×512的标准柯达彩色图像,先下采样成Bayer型CFA图像,然后完成CFA插值。

4.1 可行性验证

为了验证Bayer-CFA方法的有效性,分别进行以下两个实验。

(1)验证梯度修正对插值精度的影响。

利用客观指标作为目标函数,k1在区间[0.5,0.95]以0.05的步长递增,同时k2在区间[0.5,0.05]以0.05的步长递减,研究梯度修正时式(18)中涉及的权重系数,最终确定k1=0.7,k2=0.3。确定式(19)～(21)中涉及的权重系数v1和v2的方法与式(18)相同,最终得到v1=0.9,v2=0.1。

(2)验证Bayer-CFA方法的插值效果。

4.2 实验结果分析

表1 24幅图像不同方法的rCPSNR和

表1的客观数据表明,与Bayer-CFA方法相比,最具竞争力的方法是文献[4]。然而,文献[4]的rCPSNR不够稳定,24幅图像中,6幅取得了最优的效果,5幅获得了适中的效果,其余13幅获得了最差的效果。分析效果最好的6幅图像,发现可以将其分为两类:Kodim2、Kodim8、Kodim19属于建筑景物图;Kodim4,Kodim12、Kodim18属于人物图。分别选择一幅纹理较多的图像Kodim8和Kodim18展示主观效果图,并和Bayer-CFA方法相比较,结果见图5。

(a)文献[4]的Kodim8

(b)Bayer-CFA方法的Kodim8

(c)文献[4]的Kodim18 (d)Bayer-CFA方法的Kodim18图5 文献[4]和Bayer-CFA方法对Kodim8和Kodim18的插值结果

图5中,为展示细节,截取并放大了局部图像,Kodim8在155列385行截取分辨率为80×110的图像,Kodim18在365列255行截取分辨率185×75的图像。从图5a和5b可知,对Kodim8,文献[4]在减少伪彩色方面优于Bayer-CFA方法,在窗户等纹理较多的地方仅仅产生了少许的伪彩色。从图5c和5d的局部放大图像可知,对Kodim18,文献[4]在项链处出现的伪彩色明显少于Bayer-CFA方法,但在上下嘴唇的边缘出现了非常显眼的锯齿现象,影响视觉效果。综合上述分析,文献[4]在减少伪彩色方面取得了较好的效果,但在减少锯齿现象方面,还有待进一步改进。

图6是对Kodim19和Kodim24两幅图像利用Bayer-CFA方法插值时不使用和使用梯度修正的结果。图6a和图6c为未修正结果,在图6a的栅栏中间位置及最右侧、图6c的右侧树叶及烟筒左侧的屋顶处分别出现了明显的模糊和伪彩色。图6b和图6d是修正的结果,减少了上述伪彩色,很好地改善了图像质量。可见,梯度修正能够提高插值精度。

分别使用文献[3]、文献[4]、文献[7]、文献[9]、文献[10]、文献[12]和本文方法对Kodim7和Kodim20图像进行CFA插值,结果见图7和图8。

图7是从Kodim7图像的338列144行处截取的分辨率为175×100的局部放大图像,可以看出:文献[7]的花瓣和右上的树叶出现了明显的伪彩色,右下角的树叶边缘有锯齿现象;文献[4]、文献[10]和文献[12]的花瓣上的伪彩色有所改善,但右下角的树叶仍有明显的锯齿;文献[3]仅在右下角的树叶上出现少许锯齿;文献[9]获得了和Bayer-CFA方法相当的效果,仅在树枝上的叶茎处出现了少许伪彩色;Bayer-CFA方法获得了最好的插值效果,没有出现伪彩色和锯齿,很好地保护了图像的边缘纹理细节。

(a)Kodim19不使用梯度修正

(b)Kodim19使用梯度修正

(c)Kodim24不使用梯度修正

(d)Kodim24使用梯度修正

(a)原图 (b)文献[3]结果 (c)文献[4]结果

(d)文献[7]结果 (e)文献[9]结果 (f)文献[10]结果

(g)文献[12]结果 (h)文本结果 图7 不同方法对Kodim7进行CFA插值后的局部放大结果

(a)原图 (b)文献[3]结果 (c)文献[4]结果

(g)文献[12]结果 (h)文本结果 图8 不同方法对Kodim20CFA插值后的局部放大结果

图8是从Kodim20图像的244列265行处截取的分辨率为150×70的局部放大图像,可以看出:文献[4]的字母周围和小女孩的轮廓处均有严重的伪彩色;文献[9]、文献[10]和文献[12]的伪彩色明显减少,尤其在小女孩的轮廓处明显改善;文献[3]和文献[7]的插值效果较好,文献[7]在字母E的中间一横的上边及字符串周围出现了少许伪彩色,而[3]消除了字母E的处的伪彩色;Bayer-CFA方法的CFA插值质量最高,没有出现伪彩色和锯齿,很好地保护了图像的边缘。

4.3 算法复杂度分析

操作算子的个数取决于测试图像,大O阶法通过统计操作算子的计算次数来估计复杂度,是一种事前分析估计法,它利用循环嵌套的层数衡量时间复杂度。对分辨率为X×Y的Bayer图像,CFA插值时需要插值所有像素点,循环嵌套的层数为X×Y,时间复杂度为O(XY)。为了更好地分析算法复杂度,假设算法中每个条件出现的概率相同,表2列出了7种方法CFA插值时所需要的操作算子的计算次数。Bayer-CFA方法的操作算子计算次数仅少于文献[4]和文献[12],但是文献[4]和文献[9]需要迭代,文献[10]需要训练支持向量机,均会增加运算时间,增加算法复杂度。

表3是各种方法对Kodim19进行处理的CPU平均运行时间,可以看出,文献[7]的运行时间最短,Bayer-CFA方法落后0.078s,但比平均性能指标位居第2的文献[9]快了0.621s。综上,Bayer-CFA方法在CFA插值性能和算法复杂度上均获得了优势。

表2 不同方法操作算子的计算次数

表3 CPU平均运行时间

5 结 论

边缘像素点的插值精度是影响CFA插值效果的关键因素。本文在考虑图像相关性的基础上利用有限差分设计插值函数,结合梯度信息构造权重因子,实现对CFA插值图像上丢失像素值的更精确估计,从而更逼近连续图像。图像梯度含有边缘信息,沿着边缘方向插值能有效削弱锯齿现象。用梯度信息构造8个方向的权重因子,结合像素点的空间位置,利用距离决定8个权重因子的加权系数,完成修正后能有效提高插值精度。相较于EET和SSA方法,Bayer-CFA方法的rCPSNR分别提高了0.57dB和1.79dB,且能很好地保护图像的边缘细节。