燃气轮机拉杆转子非线性动力学特性研究

2019-04-29达琦袁奇李浦

西安交通大学学报 2019年5期

达琦,袁奇,李浦

(1.西安交通大学能源与动力工程学院,710049,西安;2.西安交通大学陕西省叶轮机械及动力装备工程实验室,710049,西安)

拉杆转子常用于重型燃气轮机和航空发动机,通过在中心或周向拉杆螺栓上施加预紧力来保证多级轮盘之间的相对静止并使轮盘段具有一定刚度。然而,即使受到较小的弯曲外载荷,转子轮盘接触面仍会部分区域脱开[1],导致接触面积减小进而造成转子整体刚度下降。文献[2]对某航空发动机的鼓筒式转子接触段刚度进行研究,结果表明轮盘之间的相对转角随弯矩线性增加呈现出非线性的变化规律。在建立具有螺栓连接结构的航空发动机转子力学模型时,常采用角刚度分段线性模型来近似连接部位的刚度变化规律[3]。与连续转子相比,角刚度分段线性模型的动力学响应与线性模型的动力学响应存在较大差异。为了解释组合转子升速和降速中存在的振幅突跳现象,有学者综合考虑轮盘接触面和拉杆刚度的共同作用,建立具有三次方刚度的转子模型[4-5]。拉杆转子的特殊结构使得连接段刚度具有非线性的变化规律,且组合式转子多个轮盘之间的接触模式可能不同,因而其动力学响应十分复杂[6];在特定条件下,幅频响应中出现的线性系统所不具有的双稳态现象使得转子故障频发,造成了巨大的经济损失。对于非线性转子系统出现的振幅突跳现象,国内外学者从不同角度进行研究[4,7-10],将其视为转子系统的一种故障,并尽量设法避免。目前国内对于拉杆转子非线性振动特性研究较少,以往的文献均采用刚度硬化模型,即整体刚度随转速增加而增加,对于幅频响应中出现的振幅突跳现象无一致结论,且现有分析模型缺乏依据。

针对以上问题,本文首先利用三维非线性有限元方法计算得到拉杆与接触面等效刚度随轮盘横向间距的变化规律;然后分别采用双线性模型和三次方模型拟合非线性刚度曲线,建立两种拉杆转子力学模型;最后通过数值仿真分析,对两组模型幅频响应中出现的非线性振动现象进行了对比研究,进而分析不同系统参数对转子振动特性的影响。

1 拉杆转子横向刚度分析

图1为周向拉杆组合式转子模型,该模型由轴头、轮毂、轮盘、拉杆和接触面组成,l3、l4分别为轮毂和轮盘的轴向长度,2l1表示轮毂和轮盘总长度,l2为轴头长,模型总长为2l。将轮盘接触面和拉杆的刚度一并考虑,Ks、Kh、Kds、Kr分别表示轴头、轮毂、轮盘和拉杆的抗弯刚度。

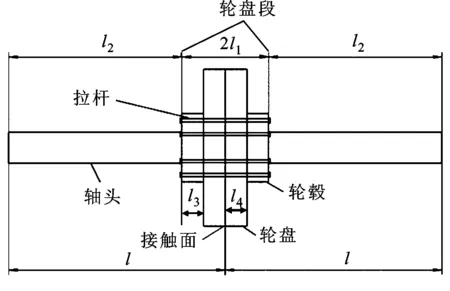
(a)拉杆转子示意图

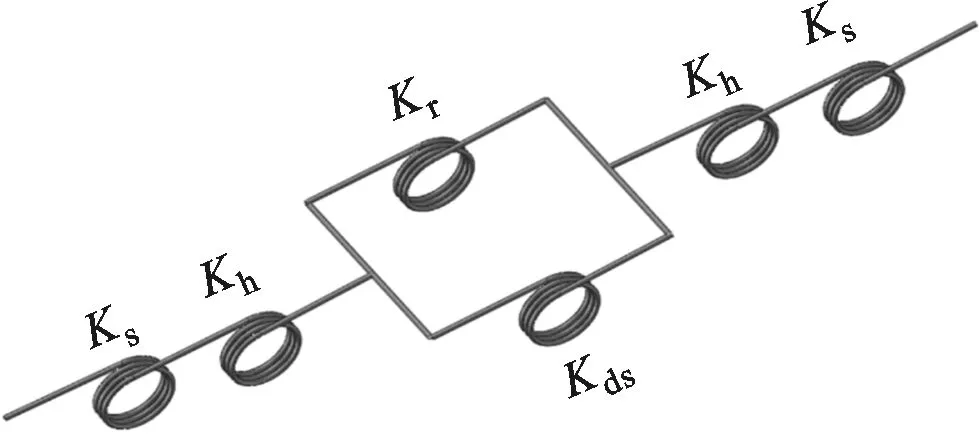
(b)转子弯曲刚度模型图1 周向拉杆组合式转子

转子轮盘段的刚度可表示为

(1)

利用弯矩-转角关系和有限元软件计算轮盘段的抗弯刚度

(2)

Kfij表示在j方向上引起转子在i方向上产生单位转角所施加的弯矩。

为简化分析,认为转子各向同性,并不计交叉方向上的刚度,弯曲刚度可以表示为

(3)

(4)

式中δij为克罗内克函数。利用式(3)可以在三维有限元软件ANSYS中求出轮盘段的抗弯刚度Kc,然后将Kc代入式(1)计算得到Kr。

用力矩-面积法求轮盘段的横向刚度

(5)

利用力矩面积法分别得到轮毂和轮盘的横向刚度Khl、Kdsl,然后根据Kcl、Khl、Kdsl和Krl之间的关系,即可得到拉杆和接触面的等效横向刚度

(6)

由于轮盘相对转角很小,认为sinφ≈φ,因此两轮盘间距X近似表示为φl,其中l为接触面到轴头的距离,横向位移与转角关系示意图如图2所示。

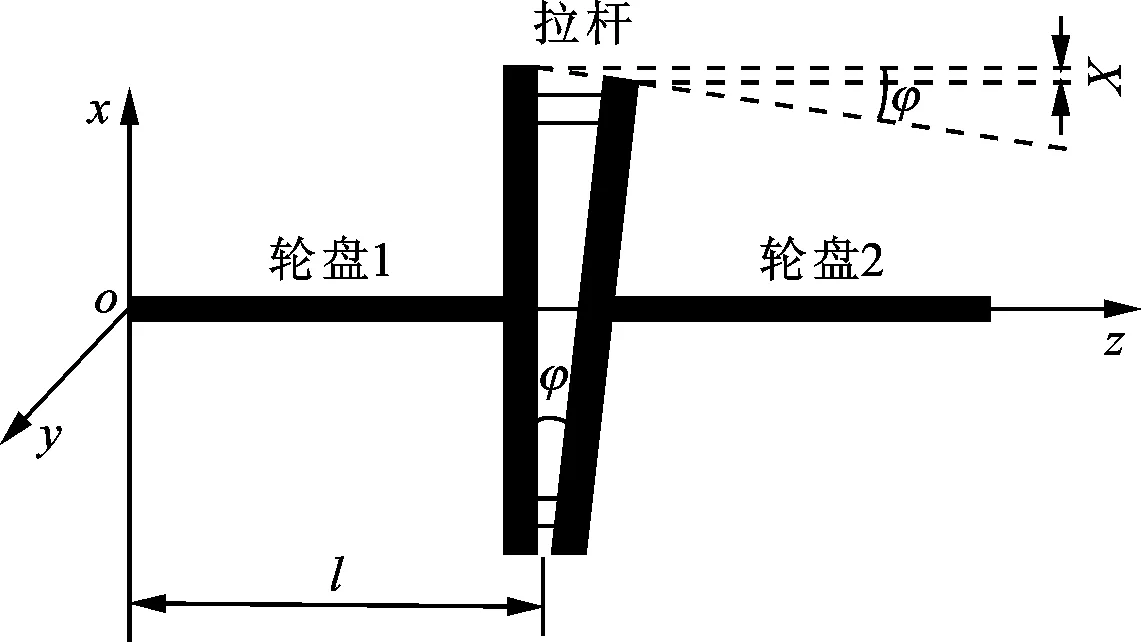
图2 转子轮盘横向位移与转角关系示意图

等效刚度对应的横向回复力可表示为

Frl=KrlX

(7)

利用有限元软件ANSYS建立上述三维有限元模型,如图3所示,模型的参数取值如表1所示。

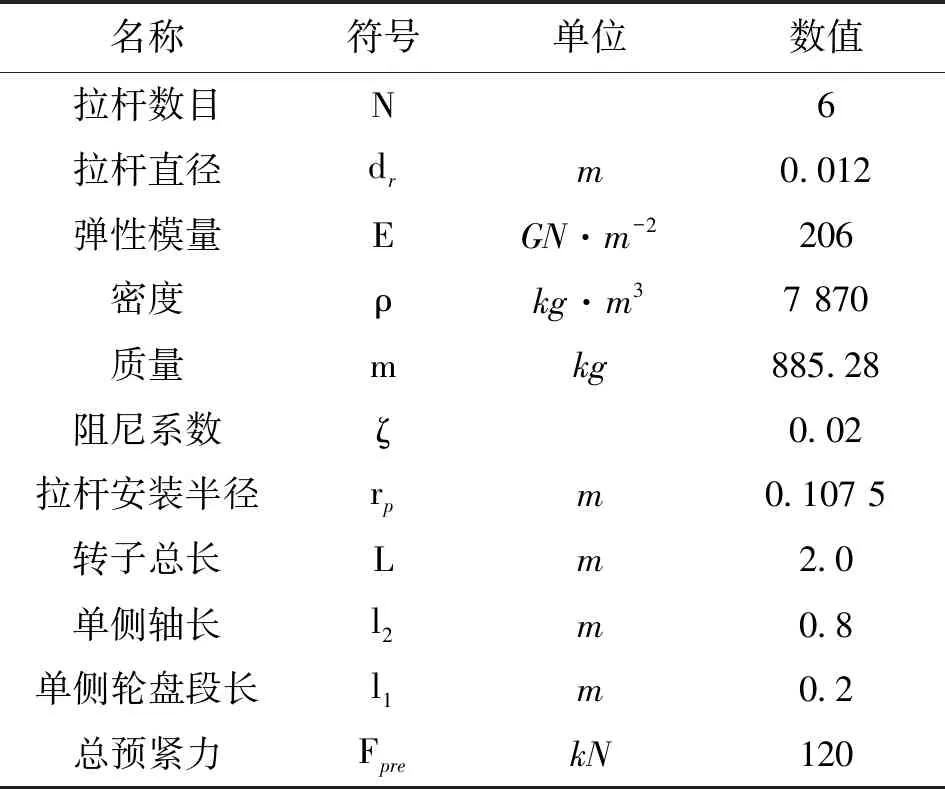
表1 模型转子物理参数

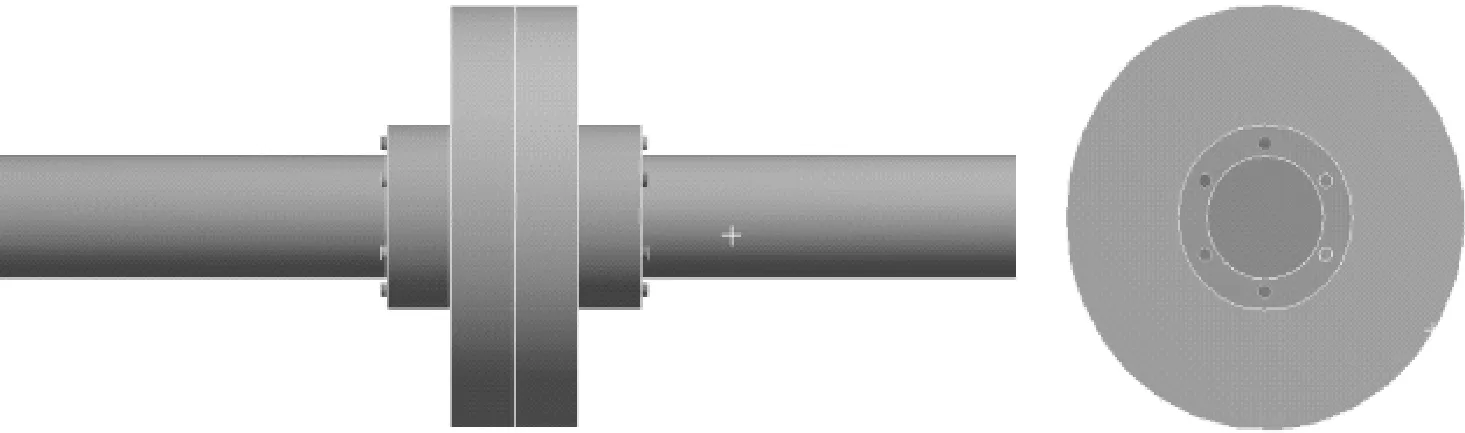
图3 拉杆转子三维有限元模型

参考文献[11]的方法,利用式(3)计算得到轮盘相对转角φ随弯矩M变化关系,如图4所示,并根据式(5)(6)计算得到等效横向刚度值|Krl|随两轮盘间距X的变化曲线,如图5所示。

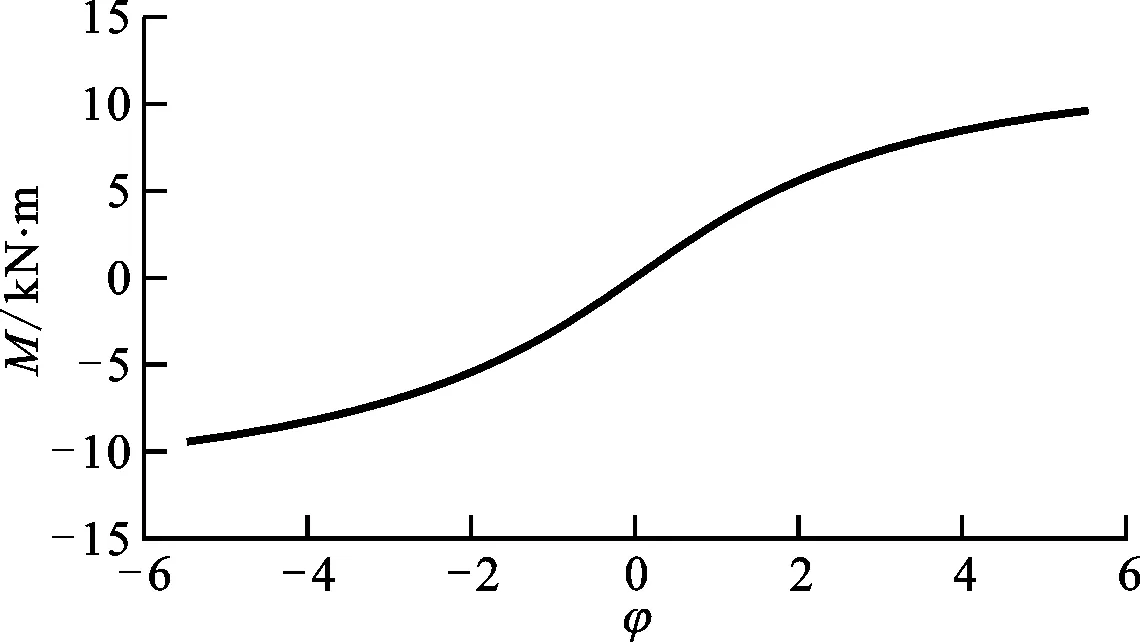
图4 轮盘间相对转角随弯矩变化关系

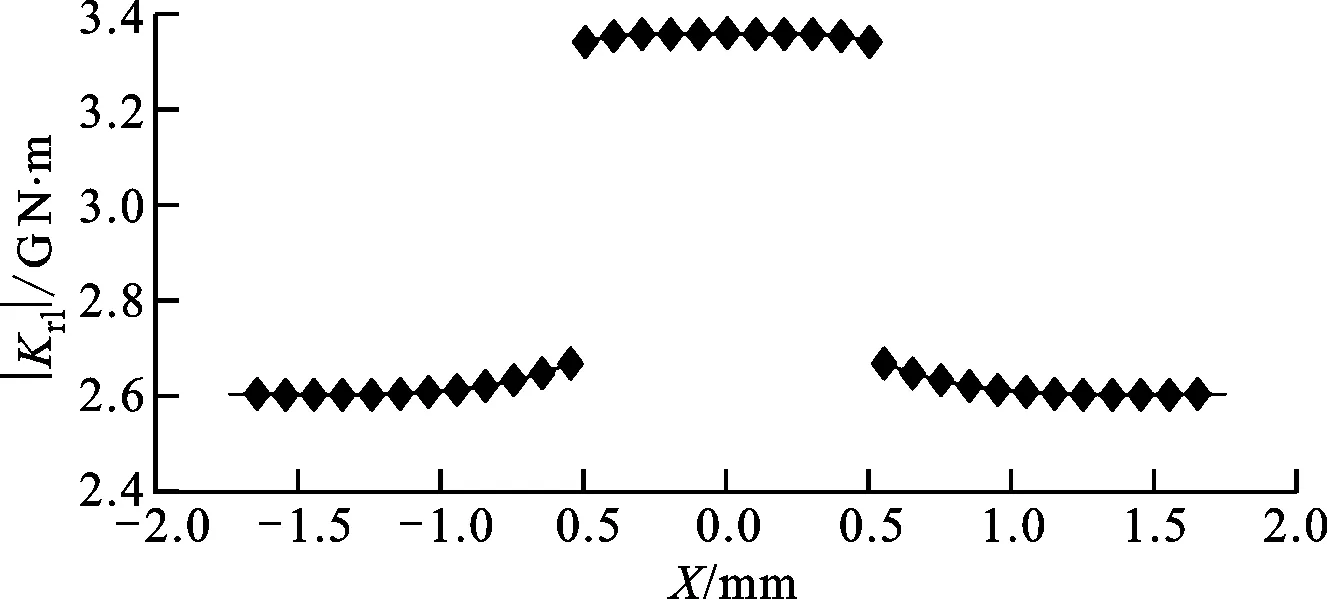
图5 等效横向刚度随轮盘间距变化曲线

2 转子动力学方程建模

将两轮盘分别简化为质量为m1、m2的刚性圆盘,两盘质量偏心量取相同值且均用e表示,偏心量矢量夹角为θ。将拉杆和接触面等效为不计质量的抗弯弹簧,回复力用F(q)表示,其中q为轮盘位移矢量。轮盘段两端分别与不计质量的弹性轴相连,两盘横向刚度分别为k1、k2。左、右端轴和抗弯弹簧的阻尼系数分别表示为c1、c2、c3。转子系统模型如图6所示。

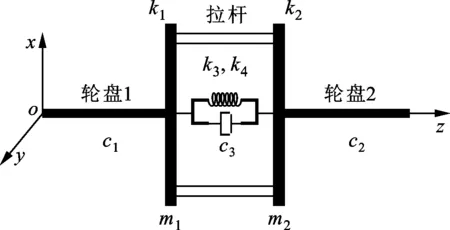
图6 转子系统模型示意图

模型中单个轮盘的位移矢量表示为

qi=[xiyi]T

(8)

式中x、y为单个轮盘的自由度。

根据达朗贝尔原理建立系统运动方程

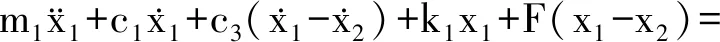
(9)

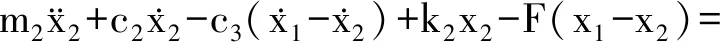
(10)

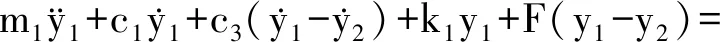
(11)

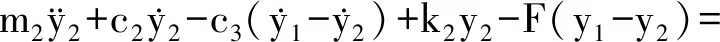
(12)

式中:Ω为转子角速度;F(x1-x2)为非线性回复力。记X=[x1x2y1y2]T,式(9)～(12)的矩阵形式为

MX″+CX′+KX=f(t,X)

(13)

式中

3 三次方非线性刚度模型

由三维有限元计算结果如图4所示,可知随着接触段载荷的增加,拉杆和接触面等效横向刚度呈非线性变化,其变化趋势可以用三次多项式函数拟合,将回复力表示为

F(x)=k3x-k4x3

(14)

式中:k3为接触段的线性刚度;k4为轮盘接触面积减小造成两轮盘横向刚度削弱后的刚度。

3.1 模型动力学方程

动力学方程在x和y方向无耦合,根据控制方程的对称性,只研究x方向的横向振动。

令τ=Ωt,x3=x1-x2,k1=β2k2=β3k3=β4k4,将式(9)～(12)改写为无量纲化形式

(15)

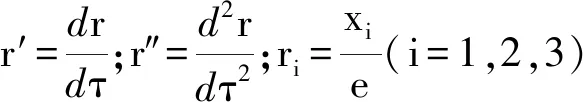
利用谐波平衡法近似求解式(13),动态响应形式解为

(16)

(17)

利用迭代算法求解式(17),可得方程组的近似解。

3.2 非线性代数方程组优化求解算法

3.2.1Broyden迭代算法Broyden算法具有超线性收敛速度,在一定条件下收敛速度快[12-13]。迭代过程可表示为

r(k+1)=r(k)-Ak-1f(r(k))

(18)

Aksk=yk

(19)

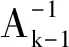
(20)

当残差小于误差限时求解收敛。

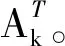
(21)

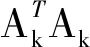
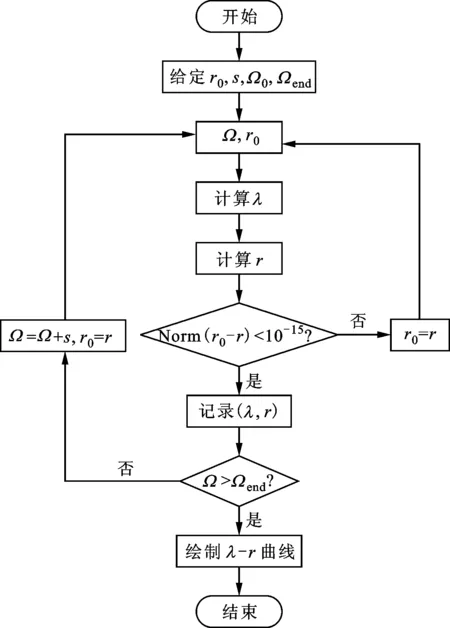
图7 模型转子幅频曲线计算流程图

3.3 计算结果与分析

计算时使用系统参数如表2所示。根据计算结果绘制拉杆转子在升速和降速过程中的无量纲幅频响应曲线,进而改变系统参数,分析不同系统参数对响应曲线的影响。

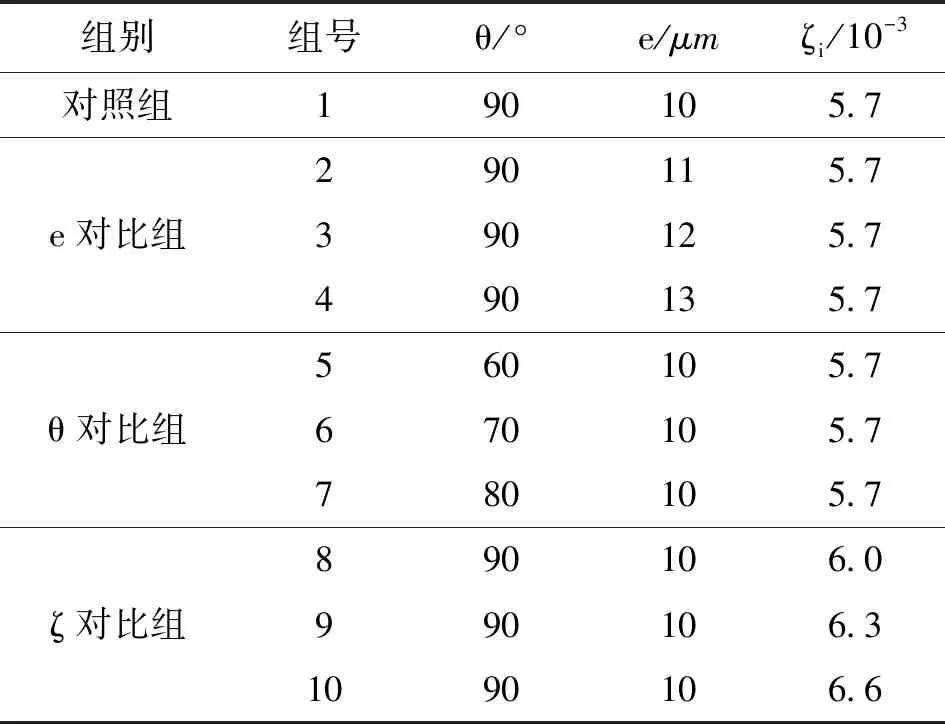
表2 拉杆转子非线性系统参数取值

3.3.1 转子升速和降速曲线取表2中第1组参数,其余参数α=0.75,β2=1,β3=1,β4=5×105m-2,绘制轮盘质心x方向的相对幅值r随转子相对转速λ变化曲线,如图8所示,图中rij表示第i个转盘的j阶谐波响应。由图8可知:无量纲幅频曲线具有一阶、三阶谐波,二阶谐波幅值过小;两轮盘无量纲幅频响应曲线随无量纲转速变化趋势相同,但幅值不同。

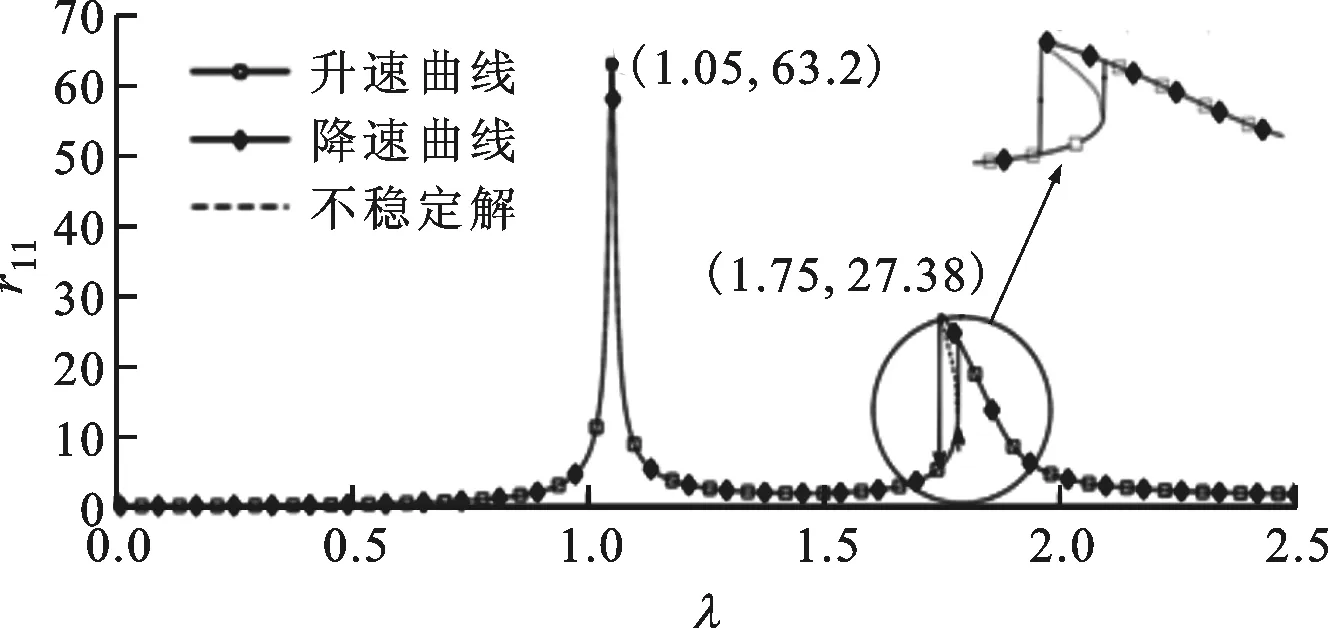
(a)轮盘1升速和降速一阶谐波曲线

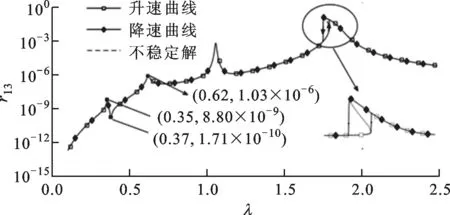
(b)轮盘1升速和降速三阶谐波曲线

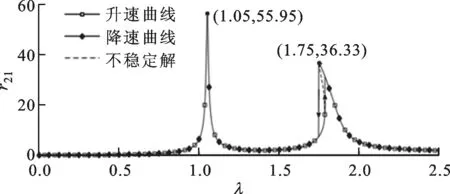
(c)轮盘2升速和降速一阶谐波曲线

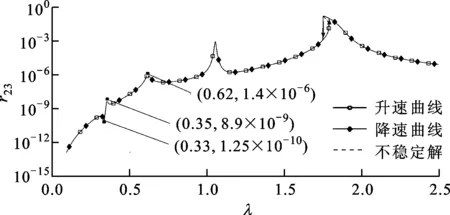
(d)轮盘2升速和降速三阶谐波曲线图8 拉杆转子轮盘升速/降速幅频特性曲线

比较β4=0(即无非线性刚度项)与β4=5×105m-2时轮盘1的一阶谐波曲线,如图9所示,可知非线性刚度使得转子二阶共振转速发生了明显的变化,但一阶共振转速变化相对不大。

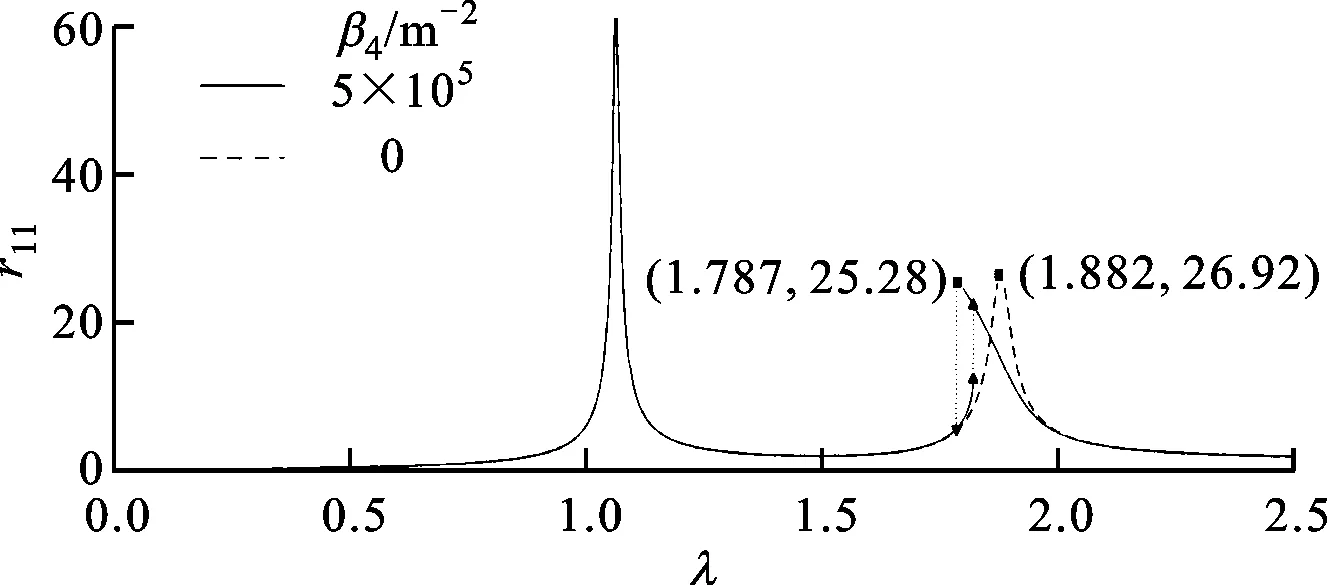
图9 拉杆转子轮盘1一阶谐波对比曲线

图8所示的无量纲幅频曲线在λ<1时,三阶谐波曲线的两个共振峰分别对应一阶、二阶固有频率的1/3次谐波。次谐波的出现表明三次方刚度模型受到非线性刚度项的影响表现出与线性模型不同的振动响应特性。一阶、三阶谐波曲线均可观察到振幅突跳现象,但升速、降速曲线发生突跳的位置不同。这是因为动力学方程中存在非线性项,使同一转速下的方程存在多解。

根据解的稳定性判断方法[15],将解分为稳定解和不稳定解。不稳定解不能长期存在,因此随着系统参数的变化,无量纲幅值作为微分方程组的解从单解区域进入不稳定区域(同样也是多解区域)时,会发生从一个稳定解突跳至另一个稳定解的行为。由于系统控制方程只在特定的频率范围存在多解区域,在模拟升速或者降速时,由于进入多解区域时对应的频率不同,使得振幅突跳位置不同。

3.3.2 结构参数对振动特性的影响为分析系统响应出现的振幅突跳现象,有必要研究系统参数对解响应曲线的影响。取表2中参数,分别比较偏心量e、不平衡量夹角θ和无量纲阻尼系数ζ在不同取值下所对应的升速幅频响应曲线,其余参数β2=β3=1,β4=5×105m-2。考虑到左右轮盘振动规律类似,非线性现象主要发生在系统二阶固有频率处,且二阶、三阶谐波相比一阶谐波幅值过小,因此只绘制轮盘1的一阶谐波在其第2阶共振频率附近的图像。

模型转子不同参数对响应曲线影响对比如图10所示,可知增加偏心量e或两轮盘间不平衡量夹角θ,减小无量纲阻尼系数ζ都会使得第2阶共振峰向左方倾斜,并使多解存在的范围扩大。

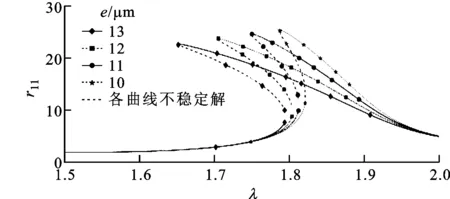
(a)偏心量的影响

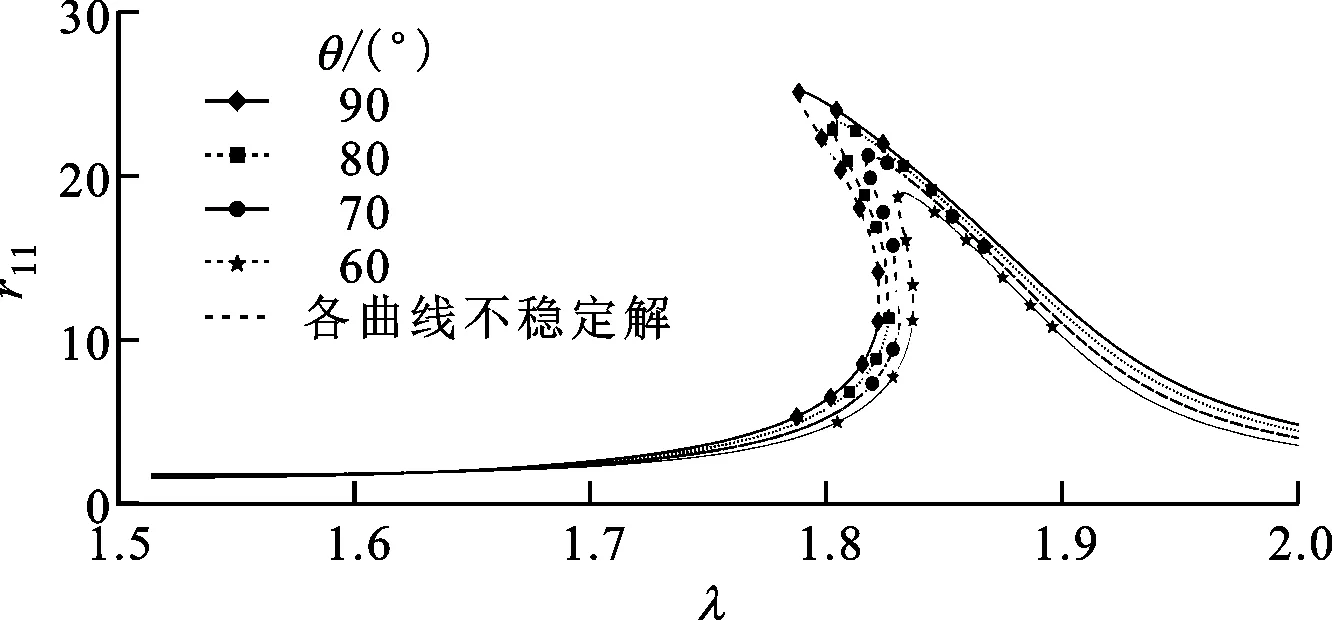
(b)两盘偏心距夹角的影响

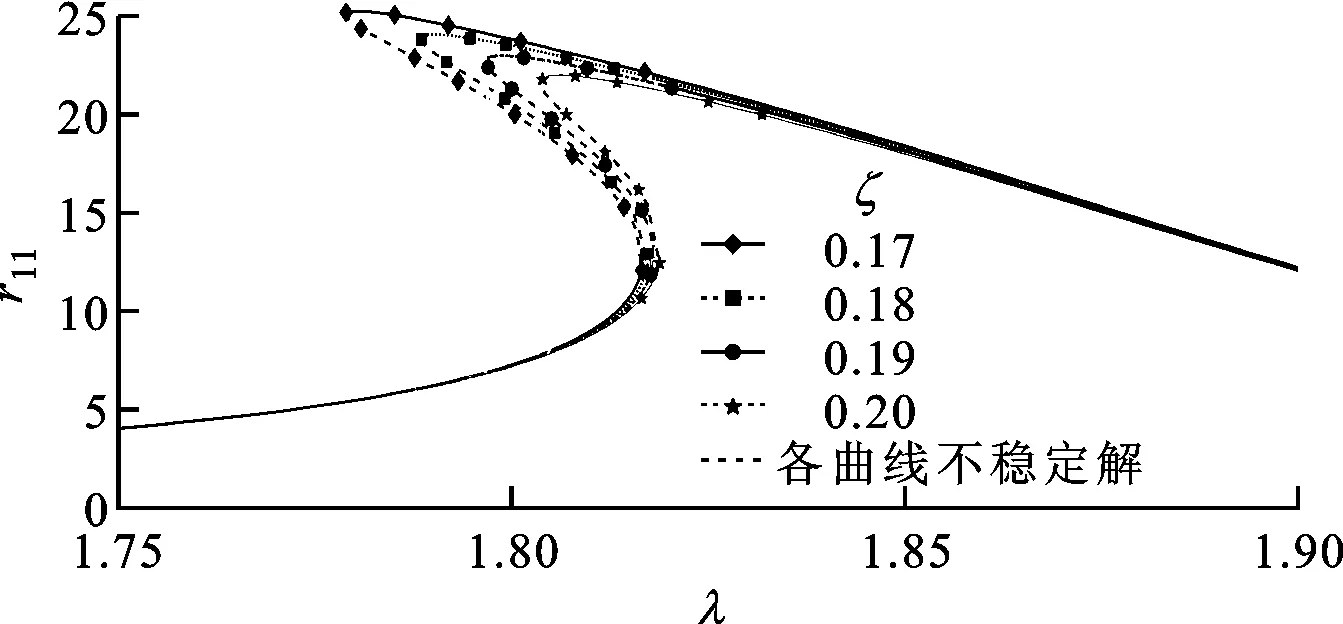
(c)无量纲阻尼的影响图10 模型转子不同参数对响应曲线的影响

不同质量比时轮盘1的幅频响应曲线如图11所示,计算参数取值见表3,其余参数θ=90°,β2=1,β3=1。由图11中可知,增加质量比会使转子系统第1阶、第2阶固有频率减小。轮盘1第2阶无量纲共振幅值随质量比增加而增大。轮盘2对应无量纲幅频曲线由于篇幅所限未展示,但其共振时无量纲幅值变化规律与轮盘1相反,第2阶无量纲共振幅值随质量比的增加而减小。

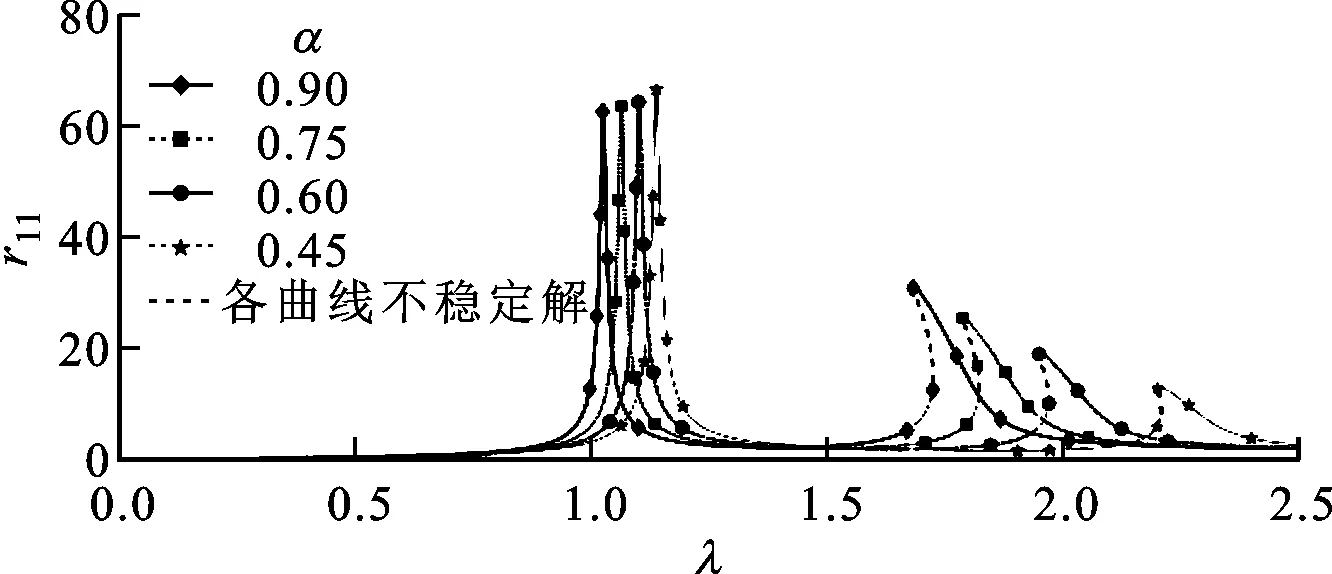
图11 不同质量比时轮盘1的幅频响应曲线

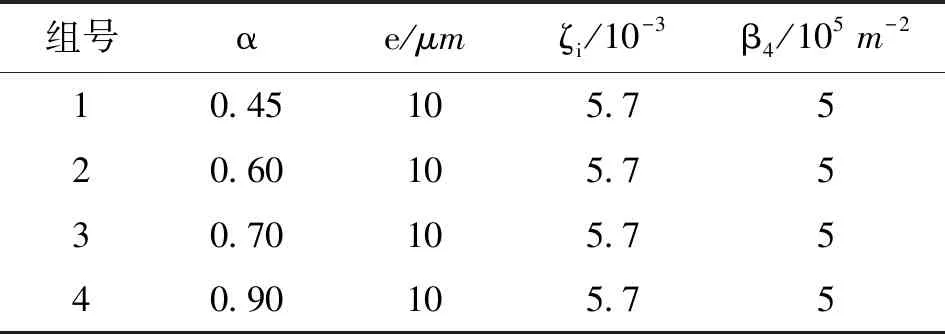
组号αe/μmζi/10-3β4/105 m-210.45105.7520.60105.7530.70105.7540.90105.75

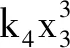
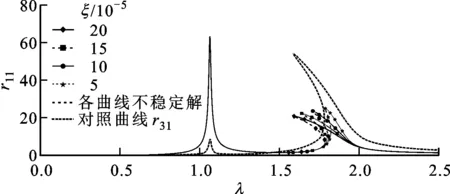
图12 非线性刚度占比对轮盘1幅频响应曲线的影响

共振峰的偏移使系统存在多解的频率范围扩大,进而使振幅不稳定区域扩大。减小轮盘偏心量,两盘偏心量夹角和非线性刚度占比,或者增加无量纲阻尼均能缩减双稳态的存在区域;而改变两轮盘之间的质量比,则能够改变振幅突跳发生的位置。

表4 对比ξ时转子系统的参数取值

3.3.3 结构参数影响分析结构参数对系统响应的影响结果可从能量和非线性刚度影响作用强弱的角度进行分析。

(1)由式(15)可知,增加偏心量e相当于增加非线性刚度占比ξ,同时具有减小拉杆刚度的作用。随着偏心量增加,非线性刚度影响增大但总刚度减小,轮盘1的响应曲线不稳定区域即解的双稳态区域变大,第2阶固有频率减小。

(2)增加不平衡量夹角会使两轮盘的位移差即(r1-r2)增大,进而使得非线性刚度k4(r1-r2)3增大,使轮盘1二阶固有频率处解存在的双稳态区域扩大。

(3)在外部输入能量不变的情况下,增加无量纲阻尼系数ζ使系统在一个周期内被阻尼消耗的能量增加,因而系统响应幅值减小。

(4)由式(15)可知,增加质量比α相当于增加轮盘1的质量比,解曲线的振幅增加而各阶固有频率减小。

4 双线性刚度模型

随着轮盘相对位移的变化,图4中关系曲线可分成斜率不同的两个部分,变化规律可近似用两段斜率不同的直线表示。假设拉杆和接触面的等效刚度随拉杆的伸长呈线性变化,则对应的回复力为

F(s)=κs

(22)

式中κ、s分别为拉杆、接触面的等效刚度和拉杆的伸长量。

固定轮盘1,接触段的横向刚度为

(23)

式中:sx为轮盘2的位移在x方向上的投影;F(s)为拉杆受到的拉力。

转子受到载荷发生弯曲,拉杆变形的形态如图13所示,用一条折线近似描述拉杆的变形。拉杆伸长在x方向上的投影为

(24)

式中:θ1、θ2分别为弯折前、后拉杆与z轴的夹角;scr为发生弯折时拉杆的伸长量。

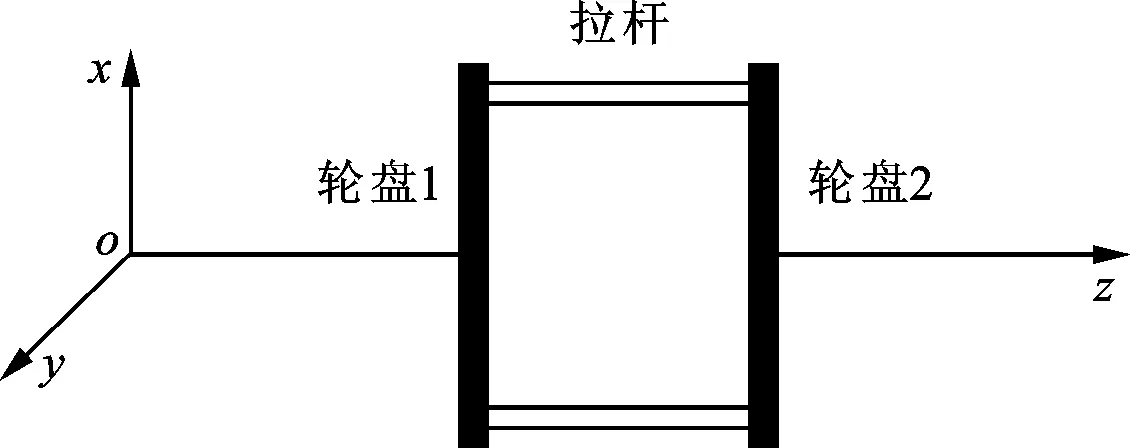
(a)未受载荷时接触部位

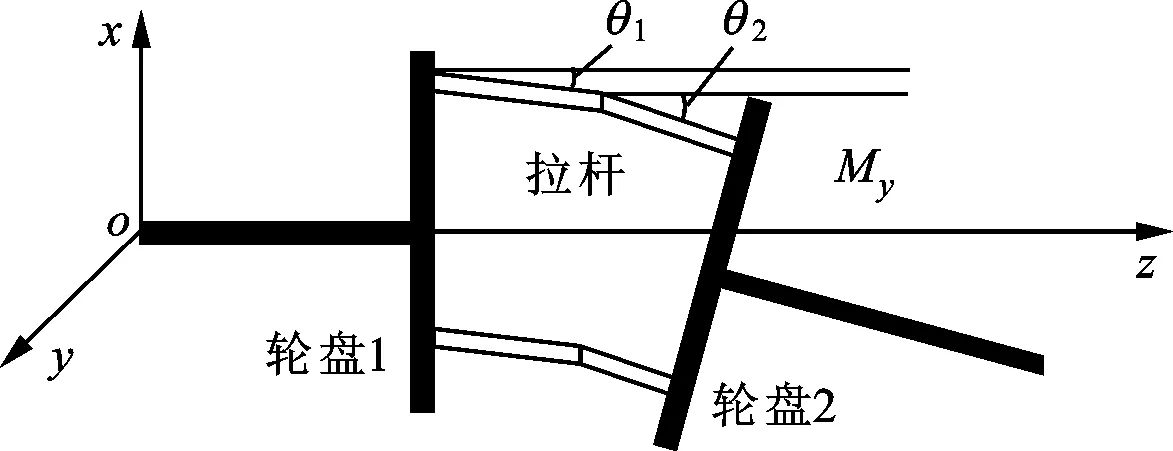
(b)受外载荷时拉杆弯曲示意图图13 拉杆受载荷变形示意图

将式(22)(24)代入式(23)可得

(25)

用x代替sx表示轮盘的横向位移,由式(24)可知等效横向刚度呈双线性,结果如图14所示。与有限元刚度计算结果对比可知,两个模型等效回复力曲线相符合,双线性模型可近似反映刚度的变化趋势,图14中两斜率关系为kl2=0.8kl1。

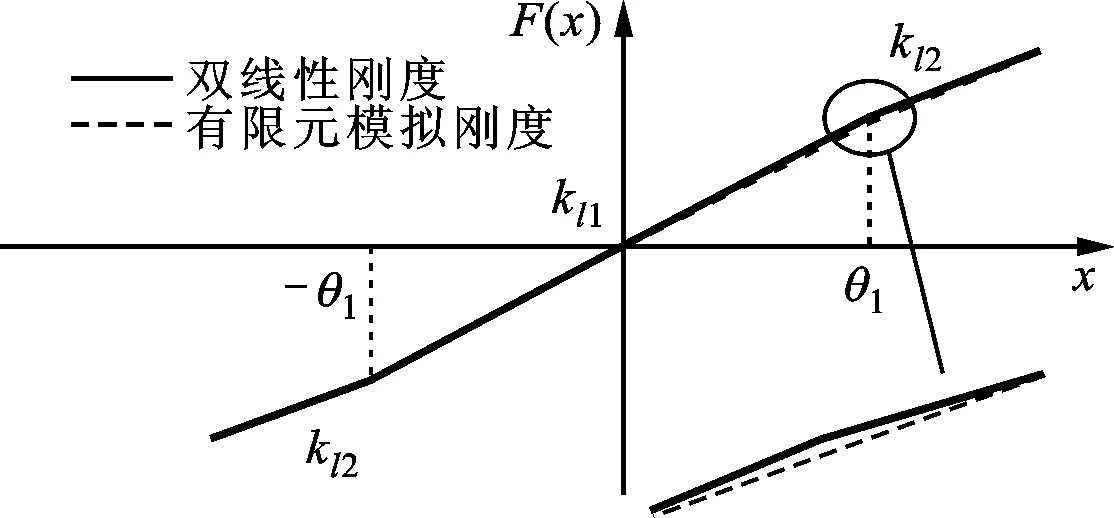
图14 双线性刚度及与有限元模拟刚度对比

4.1 双线性刚度模型动力学方程

设xcr为拉杆发生临界弯折时在x方向上的伸长量,则

xcr=scrsinθ1

(26)

记单个圆盘各方向的横向刚度为

(27)

将式(23)(24)代入式(14),得到双线性模型的控制方程组

(28)

定义函数

(29)

式中:rcr=xcr/e为拉杆弯折时的无量纲阈值;βli=kli/k1(i=1,2)为等效刚度与轮盘1刚度的比值;γ=βl2/βl1为弯折前、后刚度的比值。

4.2 转子稳态响应行为分析

取不同转速Ω,并使用4阶龙格-库塔方法求解式(28),记录稳态响应幅值。取无量纲阻尼系数ζ1=ζ2=ζ3=0.01,α=0.75,γ=0.7,rcr=10,β2=βl1=1,计算得到无量纲幅频曲线,如图15所示,可知双线性模型无量纲幅频曲线中同样出现了振幅突跳现象。轮盘2的无量纲幅频响应曲线与轮盘1的类似。

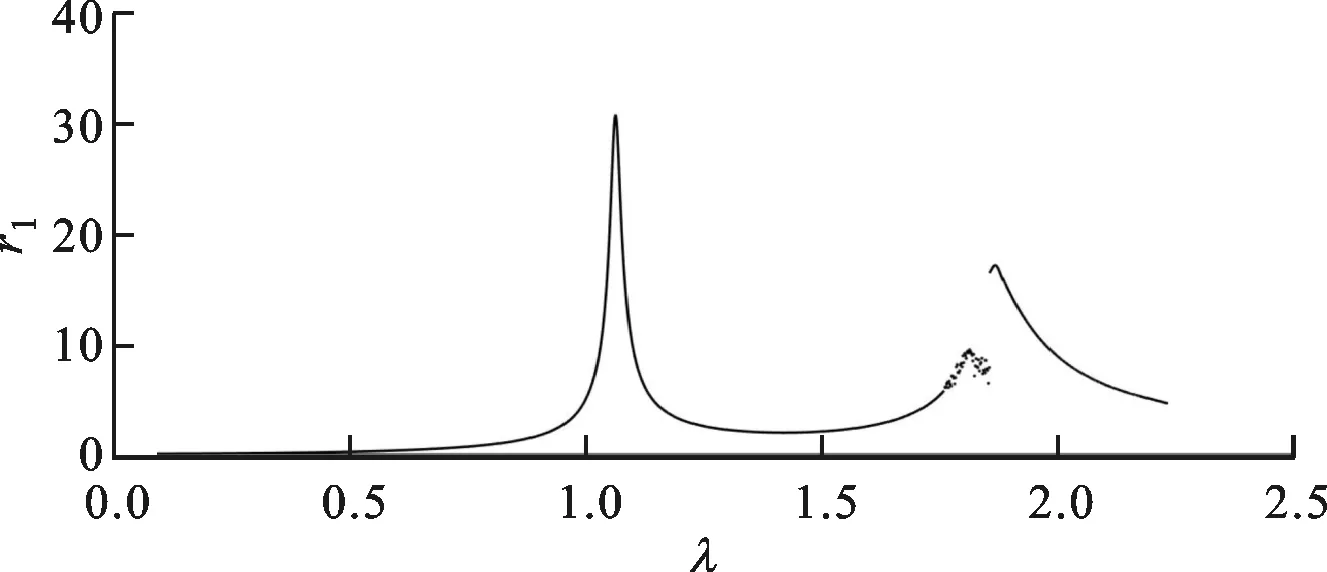
图15 转子双线性模型轮盘1幅频响应曲线

无量纲幅频响应曲线中出现的振幅突跳现象由刚度突变造成。当r1与r2的差值接近rcr并且不断增大时,响应曲线先是经历了一个振荡区域,在此范围内,无量纲振幅变化无明显规律;然后无量纲振幅突然增加,通过第二节临界转速后,随着转速增大,无量纲幅值表现出规律性的减小,如图16所示,λ取值为1.76～2.20。两轮盘位移差值随转速变化图如图17所示,可知当无量纲差值为9.17接近xcr时,响应曲线开始变得不稳定。

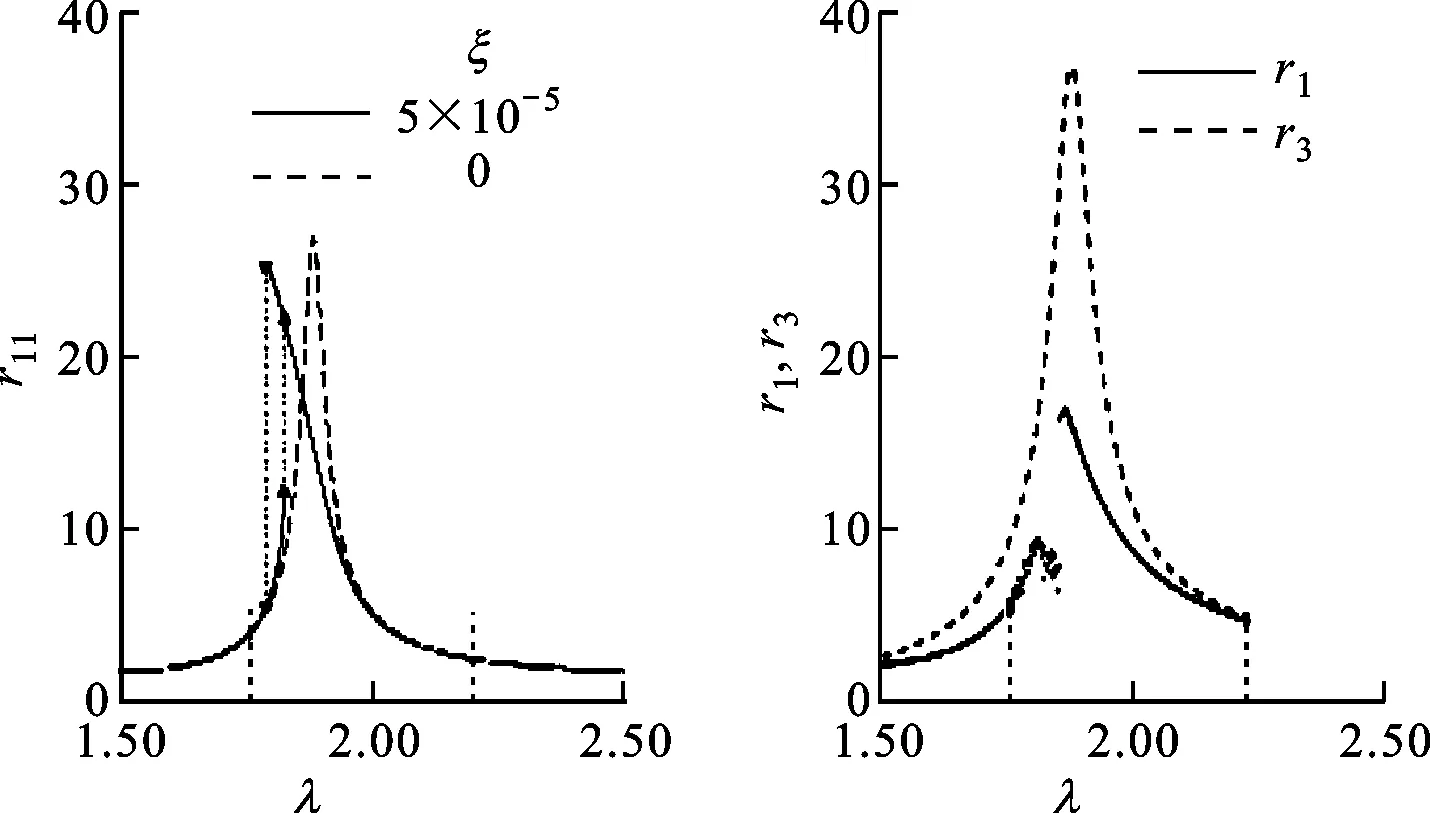
(a)模型1双稳态区域 (b)模型2不稳定区域图16 两模型不稳定区域对比

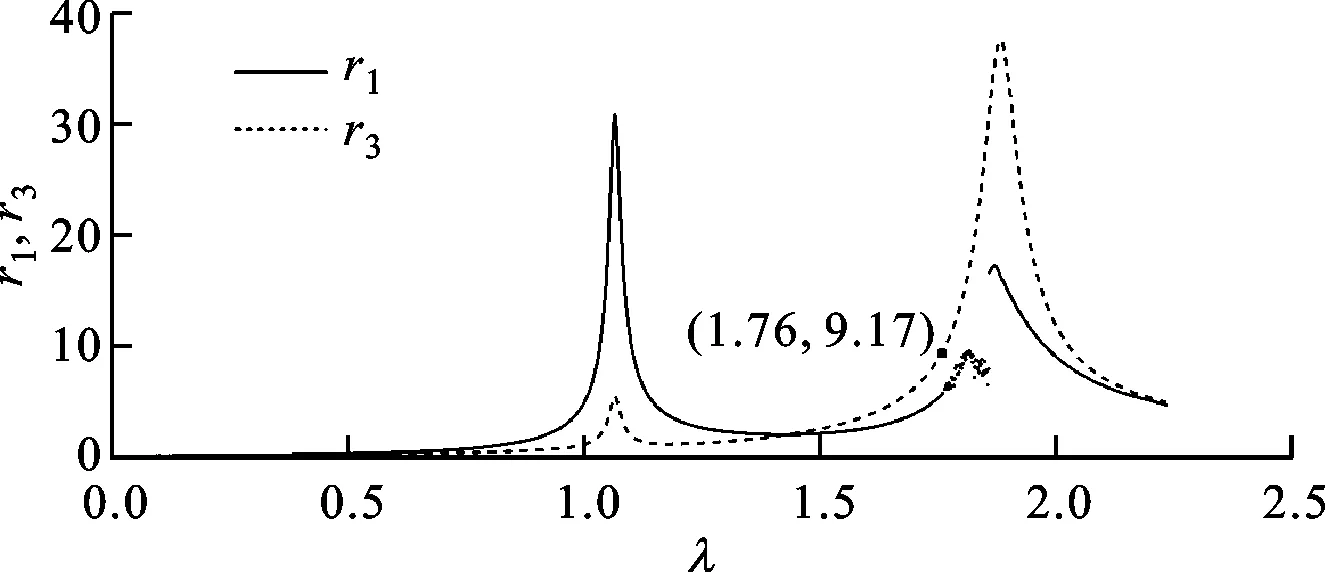
图17 两轮盘位移差值随转速变化图

4.3 三次方刚度模型与双线性刚度模型对比

采用三次方刚度模型和双线性刚度模型对有限元计算结果进行近似并分析其非线性响应,计算结果均表现出振幅突跳现象,且突跳位置基本相同。两模型差别和联系在于:三次方刚度模型的升速和降速幅频曲线振幅突跳发生的位置不同,而两个突跳之间的频段是振幅的双稳态区域。对比两个模型的计算结果得出结论:转子系统刚度非线性变化是影响振幅突跳和致使系统不稳定的原因。