高速主轴不平衡振动行为分析与抑制策略

2019-04-29章云孙虎胡振邦梅雪松

西安交通大学学报 2019年5期

章云,孙虎,胡振邦,梅雪松

(1.西安电子科技大学机电工程学院,710071,西安;2.中航工业陕西航空电气有限责任公司,713107,西安;3.西安交通大学机械制造系统工程国家重点实验室,710049,西安)

现代高品质加工表现出高速、高精度等特点,高速主轴是高品质加工的核心部件,其动态性能直接影响零件的加工的效率及精度[1-2]。主轴运行过程中,由于安装偏心、磨损等原因导致主轴惯性中心线不在主轴回转线上,即存在不平衡现象。不平衡力与转速的平方成正比,在高转速情况下,即使不平衡量微小,也会产生较大的离心力,引起主轴的不平衡振动[3]。高速加工技术中,主轴振动对加工的质量和效率影响极大,甚至导致某些功能部件的破坏。

尽管国内外学者在不平衡振动抑制问题上投入了大量精力[4-7],但工业现场时有平衡不彻底或盲目平衡的现象发生:对主轴进行低速动平衡后,即使主轴最高转速低于一阶临界,但其低速动平衡效果在高速下仍无法继续保持;以主轴不同位置测点的振动信号为依据进行动平衡配重计算,其结果往往不一致,甚至相互矛盾。这类现象在基于测试数据进行动平衡的方法中尤为明显,许多学者在动平衡实施过程中增加了主轴动力学特性信息,并在动平衡的实施过程及效果上取得了一定的进展[8-11]。

不平衡状态无法直接测量,动平衡方法的分析对象是不平衡所激发的振动响应,而不是不平衡本身。高速运转的不平衡主轴系统内部呈现非线性特征[12],这直接导致了高速下不平衡状态的逐渐演变。与此同时,各类耦合故障、复杂工况的干扰也会进一步加剧不平衡主轴的振动形态的复杂度。

因此,本文基于有限元思路,建立了主轴系统动力学模型,通过仿真与实验结合的方式对模型的有效性进行了验证,进而分析了不平衡激励下主轴转子空间振动行为,提出了基于模型的不平衡振动抑制策略,并给出了现场验证效果。

1 高速主轴系统动力学模型构建

典型的主轴有限元模型由离散质量圆盘、具有分布质量的轴段以及弹性轴承座等单元组成[13],各单元间彼此在节点处联接。主轴转子系统结构如图1所示,对于具有N个节点、其间用N-1个轴段连接而成的主轴系统,每个单元的位移向量为δ={δxn,δyn,δzn,θyn,θzn}T∈RN×1,n=1,2,…,N。

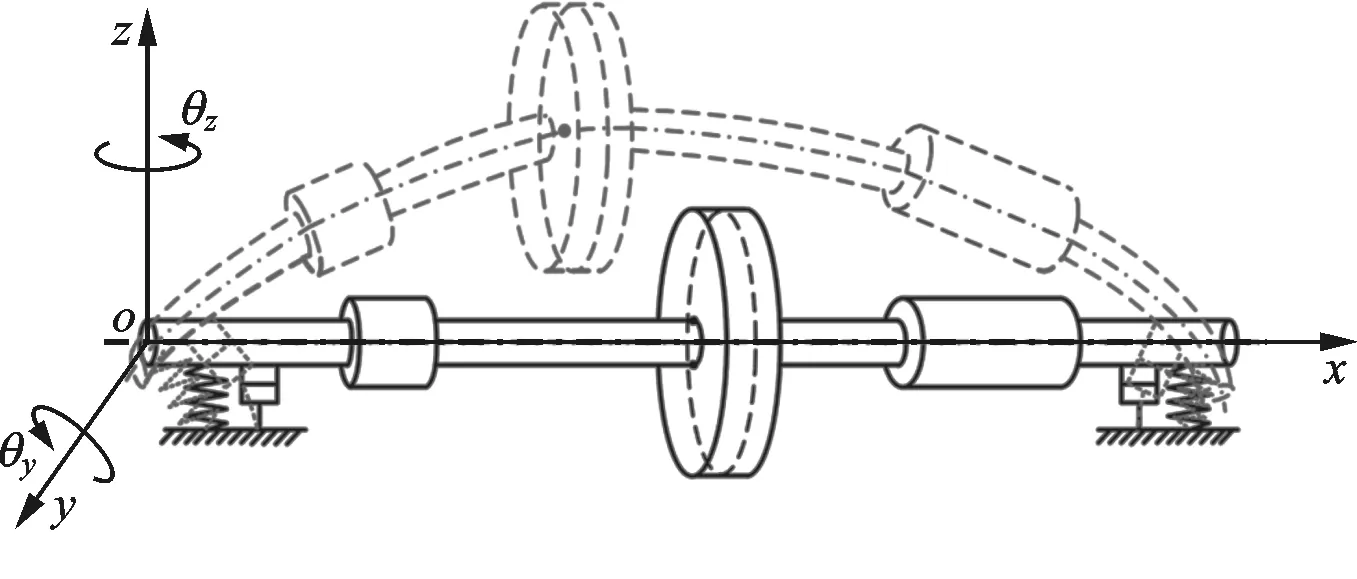
图1 主轴转子系统结构

对于采用角接触滚动球轴承支承的高速主轴,基于Jones轴承模型[14],构建由变形协调方程和力平衡方程得到的轴承滚动体非线性方程

(1)

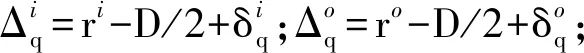
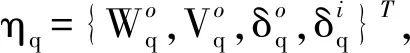
(2)

式中:τ={τ1,τ2,τ3,τ4}T为迭代误差项;λ=∂ηq/∂τ,λ∈R4×4。

基于迭代所得参数可以求解轴承的接触角与接触力,进而可得到所有滚珠与轴承内、外圈之间接触力的叠加合力Fb={Fx,Fy,Fz,My,Mz},该合力为位移向量δ的函数,将合力对位移求偏导即可得到轴承的刚度矩阵Kb。

对于主轴转子上的平衡环、编码盘以及电机绕组等质量相对集中单元,其可视为由位于圆盘中心的一个节点构成的五自由度刚性圆盘单元,单元运动方程可表示为

(3)

式中:Ω为主轴转速;Md∈R5N×5N为圆盘单元的质量单元;Gd∈R5N×5N为考虑陀螺效应的反对称矩阵;Fd∈R5N×1为圆盘偏心导致的不平衡离心力。

对于主轴转子主体部分,可视为梁单元,其有限元运动方程可写为

(4)

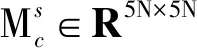
对主轴各单元矩阵进行集成,可得到主轴系统动力学有限元方程

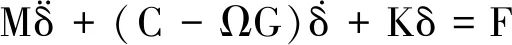
(5)

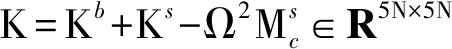
2 高速主轴系统动态特性测试

为了对主轴动力学特性进行分析,建立有限元模型,主轴转子总长为560 mm,模型中将主轴划分为58个梁单元,即共计59个单元节点,高速主轴有限元模型节点分布如图2所示。两个配重盘以及旋转编码器作为圆盘单元,其节点位置分别6、24和54,两个滚动轴承单元所在节点号为18、45。主轴转子与滚动轴承内外圈的材料密度为7.8×103kg/m3,弹性模量为208 GPa,泊松比为0.3,轴承内圈内径与外圈外径分别为25、52 mm,宽度为15 mm。轴承内共均匀分布32个滚动体,其泊松比为0.26,弹性模量为315 GPa,滚动体直径为7 mm,接触角为25°。

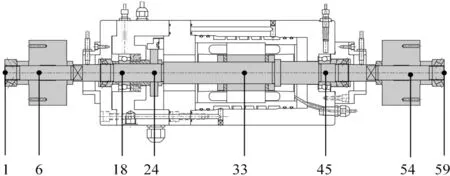
图2 高速主轴有限元模型节点分布

为验证式(5)所构建主轴动力学模型的有效性,通过Ansys商业软件进行主轴建模,其中主轴主体和轴承分别采用SOLID187和COMBI214单元构建,两者之间的连接基于接触单元TARGE170和CONTA174建立。将Ansys分析结果与基于式(5)的Matlab计算结果进行分析,弯曲振动前3阶振型的Matlab、Ansys分析结果如图3、图4所示,可知两者所求解振型的整体形貌变化规律相同。Matlab和Ansys仿真分析得到的主轴端部径向位移谐响应曲线对比图如图5所示,Matlab和Ansys仿真分析得到的前3阶谐振频率的对比见表1。

(a)1阶 (b)2阶 (c)3阶图4 弯曲振动振型Ansys分析结果

(a)1阶 (b)2阶 (c)3阶图3 弯曲振动振型Matlab分析结果

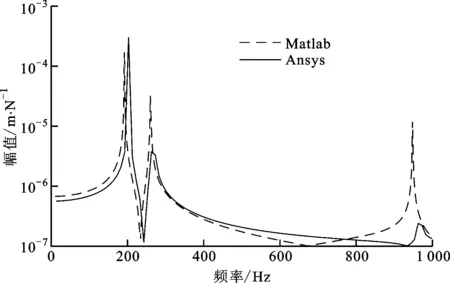
图5 Matlab和Ansys仿真分析得到的谐响应曲线对比图

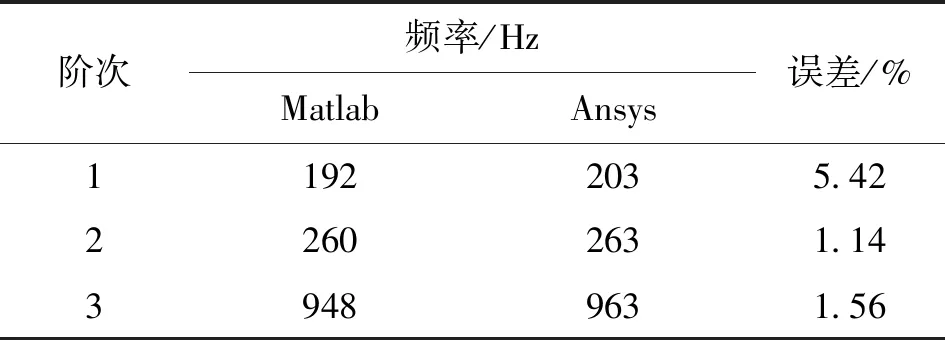
阶次频率/HzMatlabAnsys误差/%11922035.4222602631.1439489631.56

由图5、表1可知,Matlab和Ansys的频响曲线契合度很高,频响峰值处对应的固有频率误差分别为5.42%、1.14%、1.56%,由Matlab和Ansys分别计算的主轴动态特性基本相同,这反映了式(5)所建动力学模型的有效性。

高速主轴系统动态特性实验测试平台如图6所示,平台采用压电式加速度传感器ULT2001及冲击力锤LC-01A获取频率响应信息,采用电涡流位移传感器WD502A及光电传感器E32-ZC31N获取主轴不平衡振动及相位信息,数据的实时记录与显示通过INV3018CT数据采集仪来实现。

图6 高速主轴实验验证平台

在主轴末端施加激励,结合加速度传感器信号,可获得实验频率响应曲线,如图7所示。由图7可知:基于实验获取的主轴频率响应曲线的峰值分别为192.3、271.9、1 008 Hz,谐振频率的误差分别为0.16%、4.38%、5.95%,这表明仿真分析与实验结果匹配程度较高,即该模型能可靠地描述主轴的动态特性;受激励施加及响应测量位置、主轴转子装配状态、主轴系统内部组件等因素的影响,实验频率响应曲线会略有差异。在实际高速运转中,主轴谐振频率与陀螺效应、轴承特性等诸多因素相关,这会导致仿真与实测结果之间略有出入。

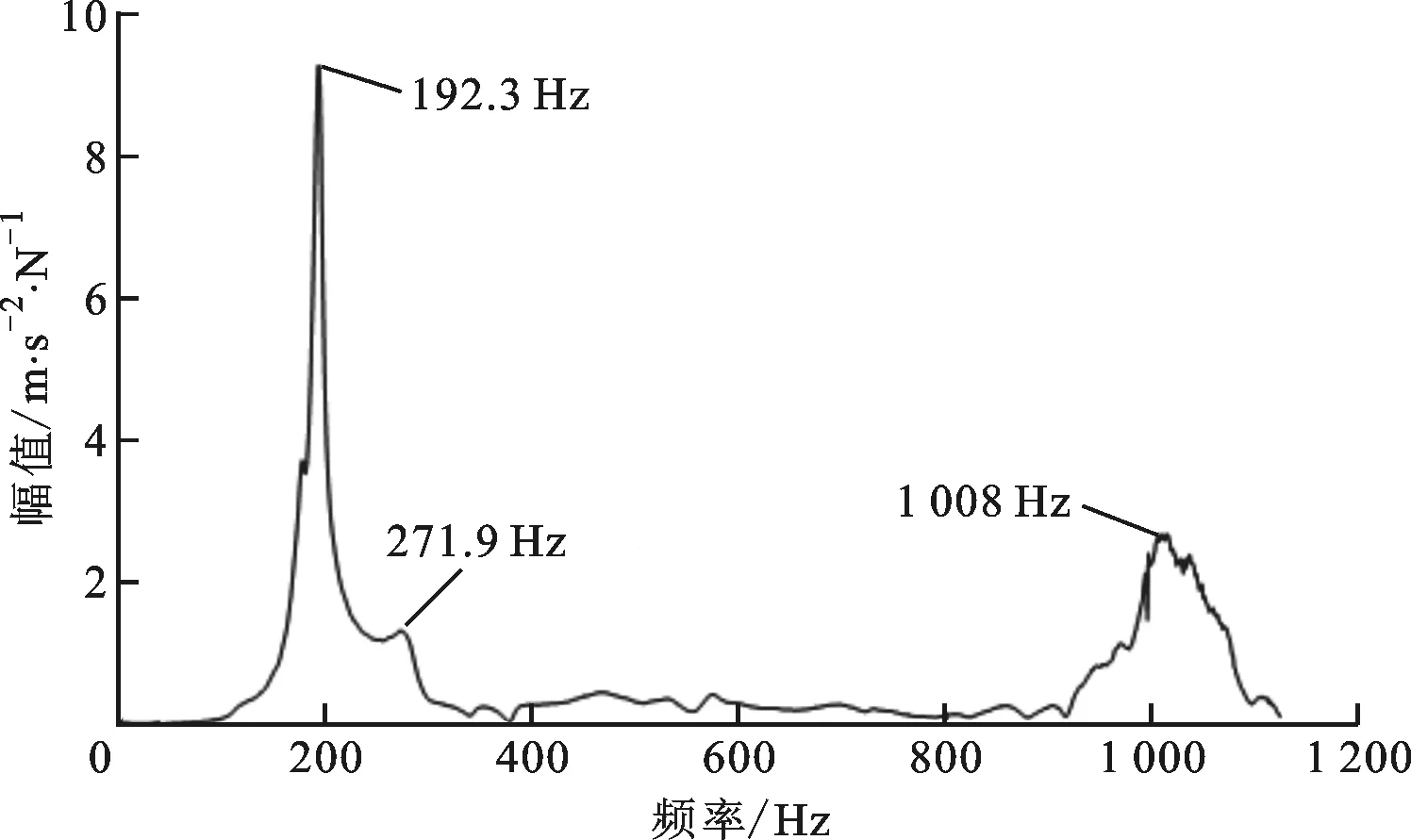
图7 高速主轴末端实验频率响应曲线

3 主轴空间振动行为分析

主轴受到不平衡激励时,将产生受迫振动,若偏心量为ε,初始相位φ0为0°,则主轴系统受到的不平衡激励可表示为

F(t)={F1(t),F2(t),…,F59(t)}T

(6)

式中Fi(t)={0,Fyi,Fzi,0,0}T(i=1,2,…,59)为每个节点上的不平衡激励,Fyi+iFzi=mεiεΩ2ei(Ω t+φ0)。

若主轴左右端节点6、54处具有不平衡质量mε6=2g、mε54=1g,ε为37mm,主轴转速为6 000r/min,不平衡激励如图8所示。在激励作用下主轴不同位置的响应不同,研究不同位置响应可以确定主轴在该激励作用下的振动传递规律。

图8 不平衡激励

不平衡激励确定后,结合有限元模型可求解不平衡响应,此处选取主轴左右端、轴承、编码器、电机绕组以及配重盘处等关键节点进行分析,根据转轴y与z向运动的相似性、对称性,以y向振动为例,yi表示y向第i(i=1,2,…,59)个节点,不平衡激励下径向和扭转响应过程如图9、图10所示。

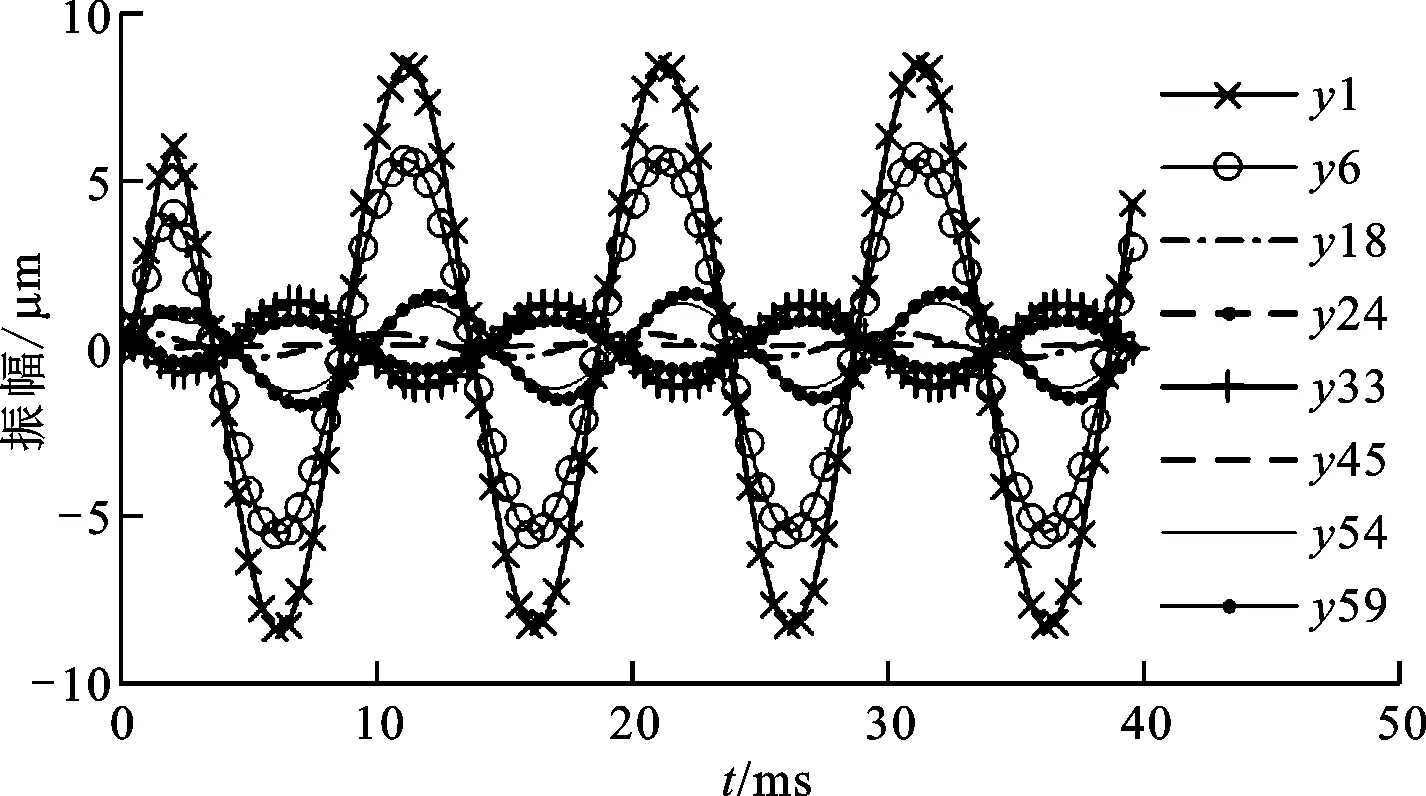
图9 不平衡激励下径向响应过程

由图9可知:在不平衡激励下,主轴振动迅速进入稳态,且不平衡振动与激励同频;主轴左右端节点1、6、54、59振动较为明显,且由于左端不平衡激励较大,故左端节点1、6振动明显大于右端节点54、59;主轴轴承节点18、45处振动受轴承外圈约束,振动幅值非常小。主轴轴承外侧节点1、6、54、59振动与两侧轴承之间的中央节点24、33振动相位近乎相反,其原因在于图3a中第1阶振型在两轴承中间位置,与轴承外侧是反向的,而当主轴运行在6 000r/min即第1阶临界转速以下时,其振动行为主要受第1阶振型影响,故符合主轴第1阶振型形貌分布特性。

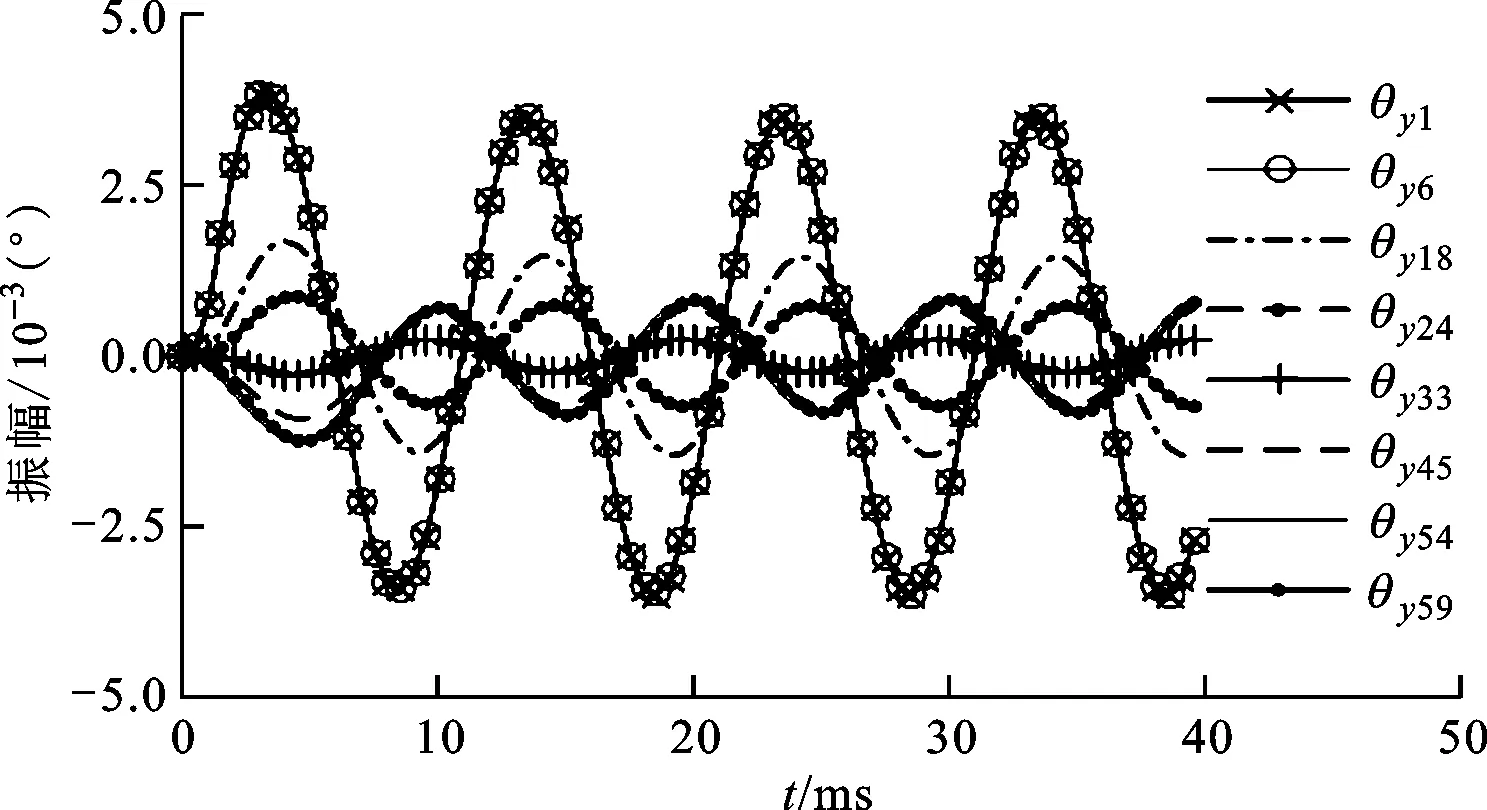
图10 不平衡激励下扭转响应过程

由图10可知:主轴左端节点1、6扭转位移明显大于右端节点54、59,符合不平衡激励左端大于右端的加载特征;轴承外端同侧延伸节点1与6、54与59的扭转位移基本一致,符合主轴轴承外侧延伸悬臂端扭转变形物理特征;轴承节点18、45处扭转位移较为明显,说明在轴承处虽然其振动幅值较小,但在该处转子偏转较为明显,这符号轴承的约束特征和图3a第1阶振型在主轴轴承处斜率较大的特征。中间节点33扭转位移最小,两侧节点扭转位移较大,主轴转子整体扭转响应符合第1阶振型曲线斜率特征。

为分析主轴转子在不同不平衡激励下的响应特性,mε54保持不变,mε6从0递增至3g,不平衡激励变化下各节点的径向响应和扭转响应如图11、图12所示。由图11可知,随着不平衡质量的增加,主轴径向位移与扭转位移均呈上升趋势,145、423mm处为轴承位置,故受不平衡质量的影响不明显,幅值较小。图12表现出同样的整体变化趋势,但因其为扭转位移,故其最小值不再在轴承处,而表现在轴承中间275mm处,该处在图11中为极值点位置,径向位移曲线斜率最小。

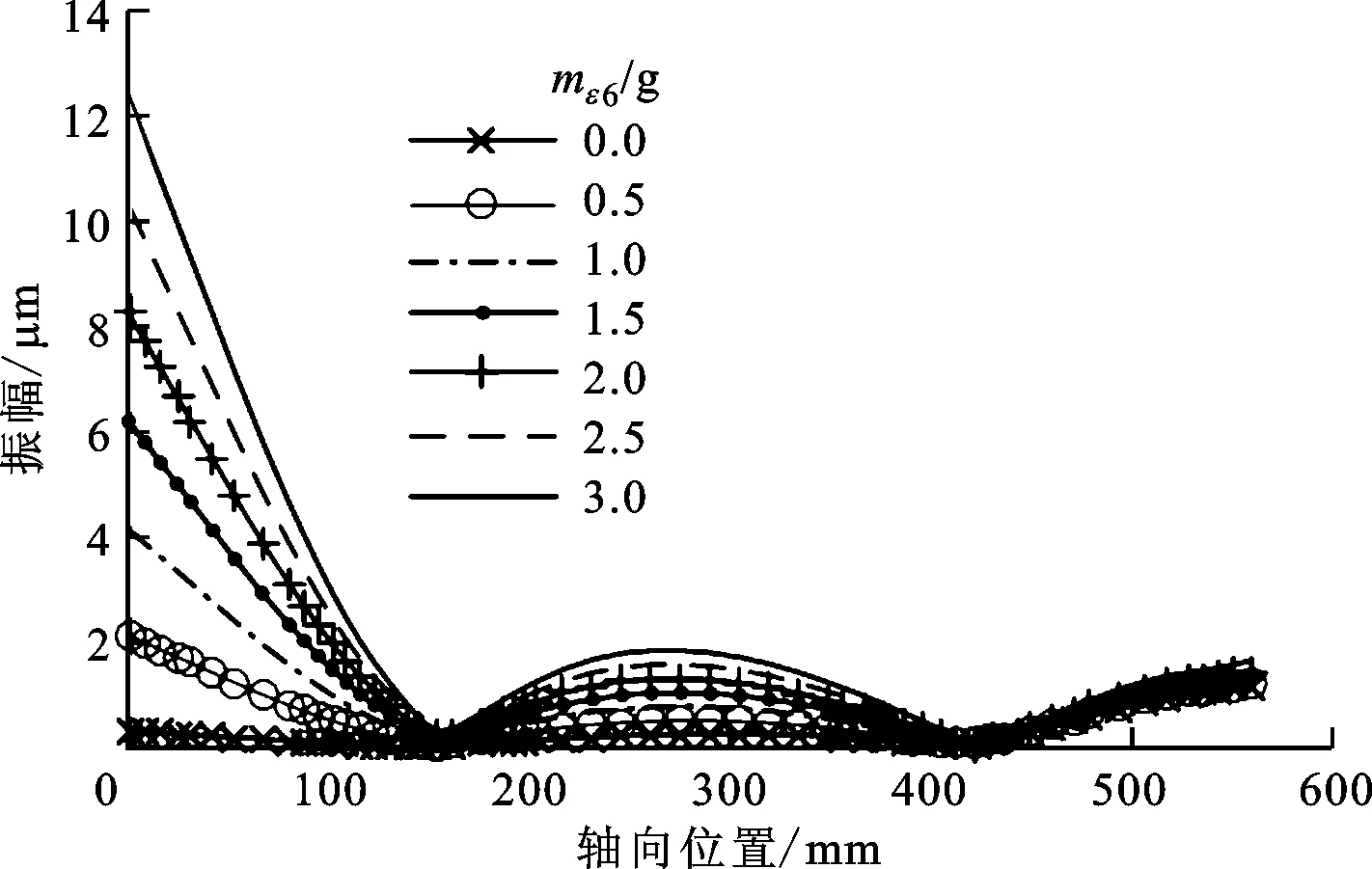
图11 不平衡激励变化下各节点的径向响应

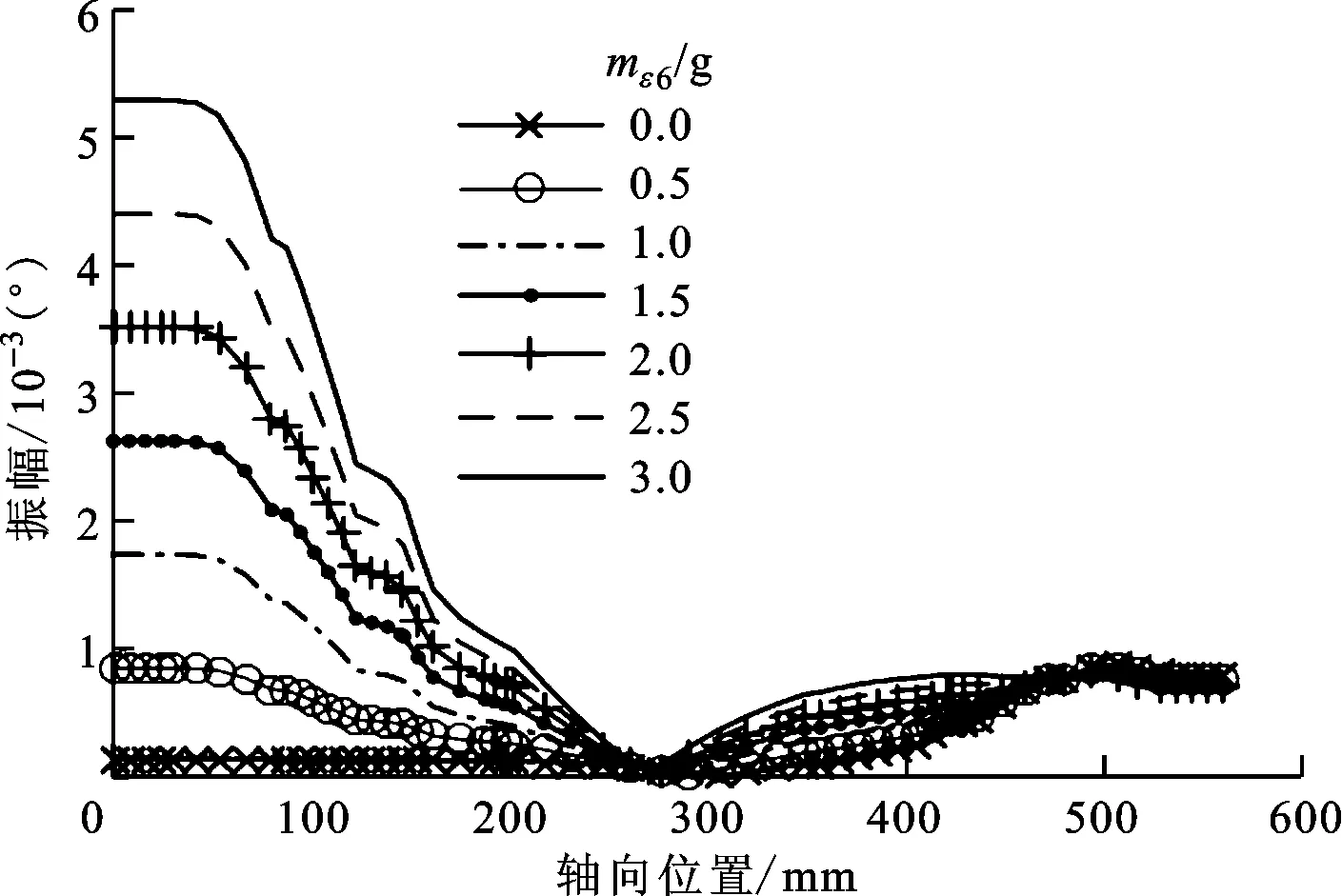
图12 不平衡激励变化下各节点的扭转响应

4 基于模型的不平衡振动抑制策略

不平衡激励会导致主轴转子空间多自由度振动,为实现空间振动的抑制,可将转子不同自由度振动按不同权重组合,构建平衡目标,但在现场平衡过程中,通常仅采用径向振动作为平衡目标,其原因一方面在于径向振动与不平衡激励的方向一致,相对于其他自由度振动,两者相关性更明显,即空间振动的平衡目标中,径向振动的权重远高于其他自由度振动;另一方面由于主轴系统的结构限制,通常仅能获取主轴径向振动。实际上,以径向振动为平衡目标,经动平衡操作后,各自由度不平衡振动都能得到有效降低[15]。

结合主轴动力学模型,可将不平衡力等效到模型节点之上,通过力学分析得出不同转速下径向振动与不平衡矢量之间的关联关系,实现不平衡量的求解。式(5)中振动响应特解为δ=AeiΩt,其中A={a1eiφ1,a2eiφ2,…,aNeiφN}T∈CN,式(5)可变形为

Ω-2[-Ω2INiΩIN-iΩ2ININ][MCGK]TA=U

(7)

式中:U={u1,u1,…,uN}T∈CN为分布在节点上的不平衡矢量;IN∈RN×N为单位对角矩阵。

若不平衡节点数为N,振动测量节点数为J,为求解不平衡矢量U,则需要测振转速的数量H为N/J,式(7)可扩展、变形为

[u1u2…uN]T

(8)

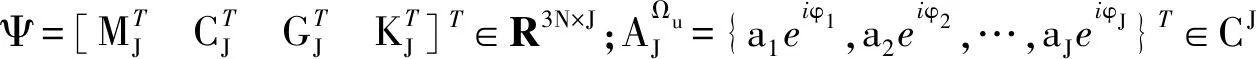
为验证动力学模型及不平衡识别策略的有效性,需开展动平衡验证。根据第1阶振型分布,不平衡振动在主轴两端体现的较为明显,实验平台上对主轴转子两端都进行监测,每个测量面上的两个电涡流位移传感器呈相互垂直方位安装,光电传感器则用于获取振动相位。由于主轴转子在装配前已进行过离线动平衡,运转时不平衡激励主要源于两侧质量盘,根据式(8),仅需一个转速即可完成不平衡激励识别,实验转速设为9 000 r/min。主轴运行稳定后,提取振动工频值,结合主轴动力学模型数据,求解得到两侧质量盘上的不平衡量分别为7.99、8.30 g·mm,所在相位分别为-179.18°、-151.88°,根据识别结果实现动平衡校正后,主轴振动抑制情况如图13所示,其中外圈三维全息谱图为原始振动,内圈谱图为平衡后的残余振动。主轴动平衡前后振动结果如表2所示。

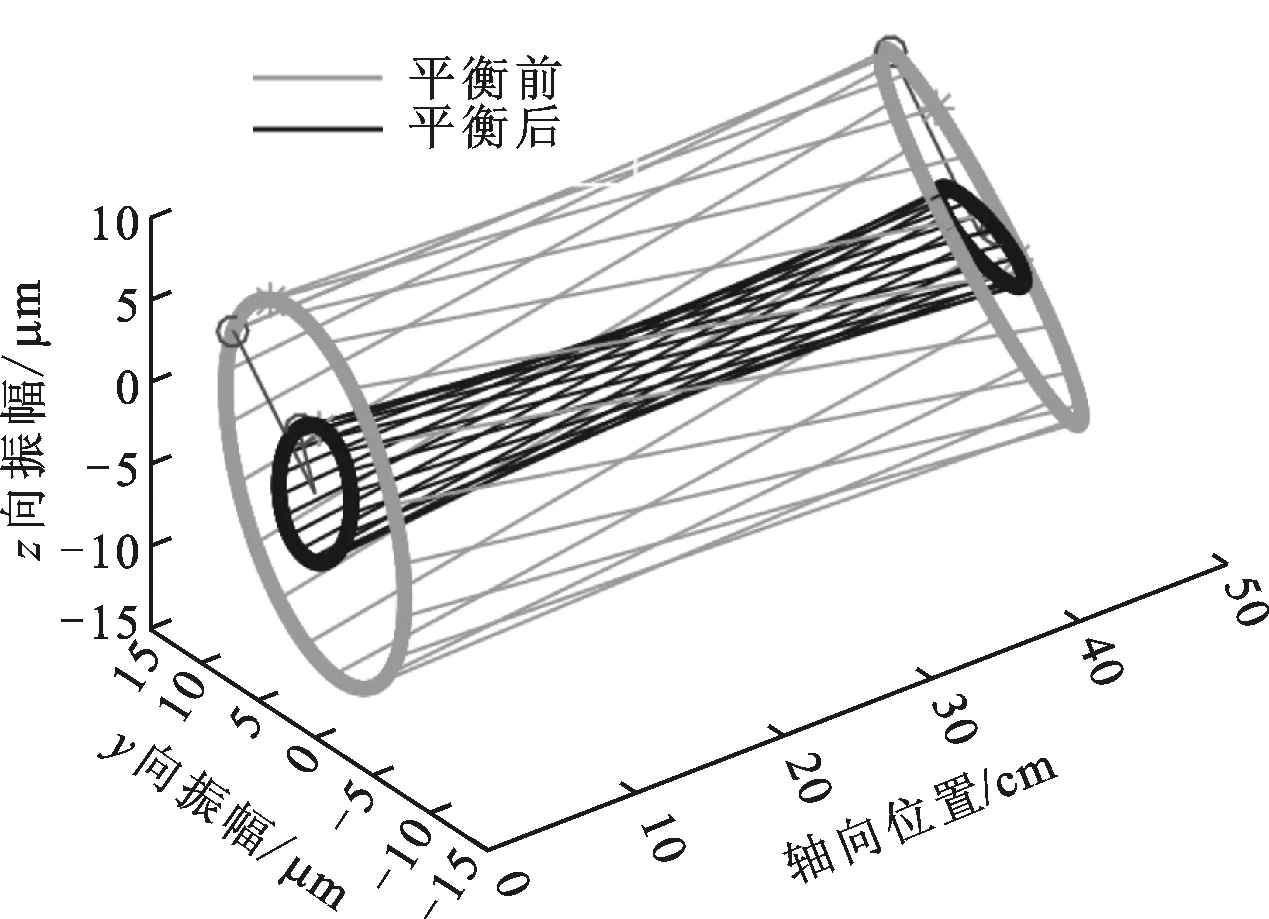
图13 主轴动平衡前后三维全息图谱对比

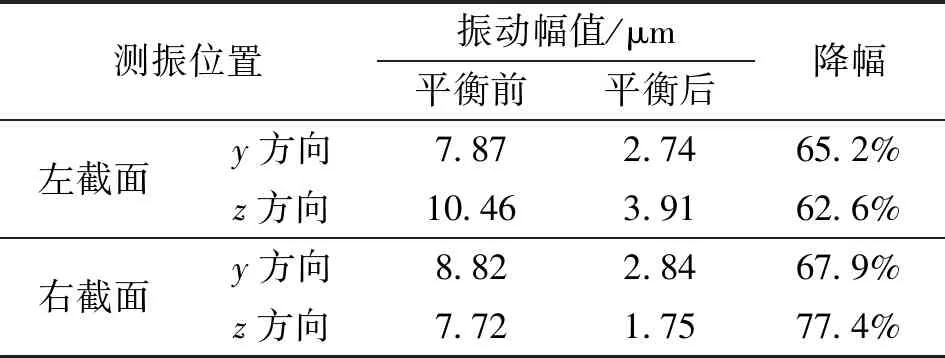
测振位置振动幅值/μm平衡前平衡后降幅左截面y方向7.872.7465.2%z方向10.463.9162.6%右截面y方向8.822.8467.9%z方向7.721.7577.4%

由图13、表2可知,主轴动平衡后,不平衡振动抑制效果较为明显,这反映了本文主轴动力学模型及不平衡振动抑制策略的有效性。图13中动平衡前后振动初相矢的方位发生了一些变化,这主要是由于平衡后振动信号的信噪比降低,提取工频振动时受噪声干扰影响,以及转子轻微各向异性所致。表2中残余振动没有降至零,主要是由于动平衡效果受到转轴弯曲等呈现工频特征的非失衡故障、配重质量加载精度以及模型构建偏差等的影响。