致密砂岩储层孔隙结构分形特征表征方法研究

孙 霞

（中石油大庆油田有限责任公司第五采油厂，黑龙江大庆163514）

致密砂岩储层孔隙结构复杂，对致密油气开发具有重要影响，但其孔隙结构表征比较困难，分形理论的发展为储层孔隙结构定量表征提供了有效手段[1⁃4]。贺承祖等[3]对常规砂岩储层孔隙结构分形特征进行了研究，并提出了分形特征表征方法，被广泛应用。马新仿等[4]提出了用分段回归方法计算孔隙结构的分形维数的方法，认为该方法能更好地反映孔隙结构的实际情况。吴浩等[5]将致密储层分形特征分为两种，一种为阶段式分形，一种为整体式分形。姜鹏等[6]研究了致密砂岩储层的分段分形特征。赵明国等[7]认为目前常用分形模型假设条件与实际存在差距，提出了考虑最大孔隙半径与最小孔隙半径比的分形模型，对现有常用分形模型进行了修正。目前广泛应用的孔隙结构分形特征表征方法多适用于常规砂岩储层，对致密砂岩储层是否适用以及致密砂岩储层是否具备分形特征等问题亟需进一步研究。本文系统梳理目前常用的孔隙结构分形特征表征方法，然后基于致密砂岩压汞实验结果对各方法适用性进行了评价并对致密砂岩储层的分形特征进行了研究。

1 孔隙结构分形特征表征方法

1.1 分形定义法

分形几何发展为不规则、复杂致密砂岩孔隙结构定量描述提供了有效手段。根据分形理论的定义，如果致密砂岩储层具有分形特征，则其孔隙数量和孔隙半径具备以下关系[8]：

式中，N(r)为致密砂岩储层孔隙的数量；r为致密砂岩储层孔隙半径；Df为致密砂岩储层分形维数。孔隙半径和相应的孔隙数量均可以通过高压压汞实验获得[9]。根据分形几何定义和式（1），在以孔隙半径为横坐标，以孔隙数量为纵坐标的双对数坐标中，致密砂岩储层孔隙数量和孔隙半径呈线性关系，致密砂岩储层分形维数可通过直线斜率求出。

1.2 Brooks⁃Corey 法

R.H.Brooks等[10]提出了一种毛管压力计算模型，见式（2）：

式中，Pc为毛管压力；Pe为进入压力，即最大进入致密砂岩最大半径孔隙对应的压力；λ为孔隙大小分布指数；S*

w为归一化湿相饱和度，见式（3）：

式中，Sw为湿相饱和度；Swr为残余湿相饱和度；SHg为进汞饱和度；SHg，max为压汞过程中的最大进汞饱和度。因此，归一化湿相饱和度可以通过高压压汞实验计算得到。

R.H.Brooks等[10]提出的计算公式为经验公式，K.W.Li[11]（2010）利用分形几何理论，从理论上推导出了R.H.Brooks等的毛管压力模型，为式（4）：

将式（4）两端取对数得：

由式（5）可知，如果致密砂岩储层具有分形特征，则在双对数坐标中，毛管压力与归一化湿相饱和度成线性关系，且直线的斜率为Df-3，文章将式（5）提供的分形特征表征方法称为Brooks⁃Corey法。

1.3 贺成祖法

贺承祖等[3]基于高压压汞实验、致密砂岩孔隙结构毛管束模型，推导出砂岩孔隙结构分形特征的表征模型:

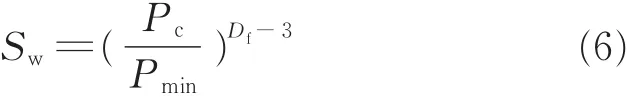
式中，Pmin为砂岩岩心进汞过程中汞进入最大孔隙半径时的压力，Sw为湿相饱和度，Pc为砂岩岩心毛管压力。

将式（6）两边取对数，得到:

由式（7）可知，根据贺成祖模型，如果致密砂岩储层孔隙结构具备分形特征，则在双对数坐标中，毛管压力与湿相饱和度成直线关系，直线段的斜率为Df-3。该方法与Brooks⁃Corey法的最大差异在于，该分形特征表征方法纵坐标为湿相饱和度，而Brooks⁃Corey法纵坐标为归一化湿相饱和度。

1.4 Li Kewen法

K.W.Li[11]推导出汞饱和度、毛管压力与分形维数之间的关系为:

式中，SHg为进汞饱和度。将式（8）两边取对数得：

根据式（9）可知，如果致密砂岩储层孔隙结构具备分形特征，则在双对数坐标中，毛管压力与汞饱和度成直线关系，直线段的斜率为Df-2。

2 高压压汞实验及结果

2.1 实验条件及步骤

实验岩样选自大庆油田FY区块致密砂岩储层，取芯深度为1 729.1～1 891.2 m，均为粉砂岩。将取芯岩样加工成直径25 mm，长度50 mm的柱状岩样；将柱状岩样放置在70℃恒温箱中蒸发岩心中水分，直至岩样重量不变为止；将蒸发后的岩样用甲苯抽提、洗净，然后烘干；测定岩样的渗透率和孔隙度，选取物性差异较大的5块岩样进行高压压汞实验（见表1）。由表1可知，选取的实验岩样渗透率分 布 在（0.04～0.90）× 10-3μm2，孔 隙 度分 布 在4%～15%，为低孔低渗储层；在室温条件下（20℃）开展高压压汞实验，测定岩样毛管压力曲线，结果如图1所示。

2.2 实验结果

由表1、图1可知，岩样物性条件对毛管压力曲线形态具有决定性影响，孔渗条件较好的岩样的毛管压力曲线位于右下方，中间平缓段较长，表明孔隙半径较大，非均质性弱；随着物性条件变差，毛管压力曲线逐渐向左上方移动，中间平缓段逐渐缩短，表明孔隙半径逐渐减小，非均质性增强。5块岩样平均孔隙半径分布在6.70～9.79 nm，排驱压力分布在0.04～0.92 MPa，束缚水饱和度分布在8.4%～33.1%。

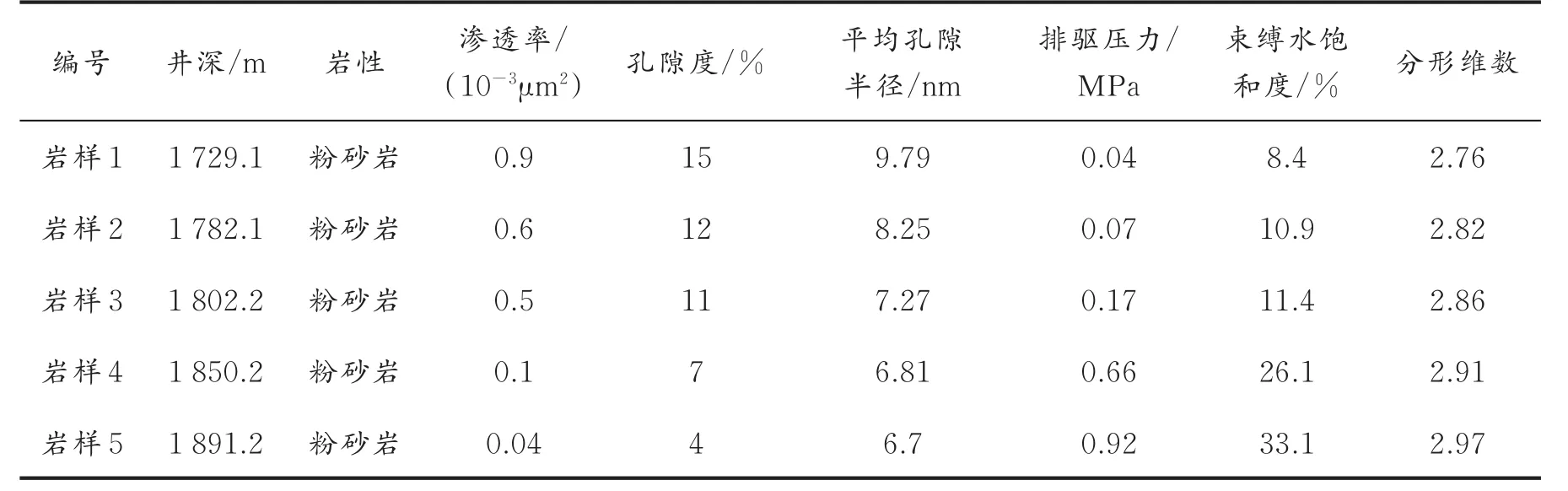
表1 实验岩样基本物性及孔隙结构特征Table 1 Basic physical properties and pore structure features of experimental samples

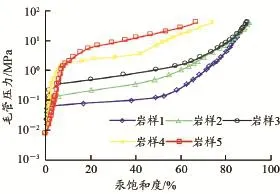
图1 5块岩样毛管压力曲线Fig.1 Capillary pressure curves for 5 samples

3 结果分析与讨论

3.1 分形特征表征方法适应性

利用上述不同孔隙结构分形特征表征方法处理致密砂岩高压压汞实验数据，分析不同表征方法对致密砂岩储层的适应性。根据式（1）作5块致密砂岩样品孔隙半径与孔隙数目关系图（见图2）。图2结果表明，在双对数坐标中，孔隙半径和孔隙数目在整个孔隙半径区间上呈线性关系，说明分形定义法能够有效表征致密砂岩孔隙结构分形特征。

图2 孔隙半径与孔隙数量关系Fig.2 Relationship between pore radius and pore numbers

根据式（5）作5块岩样毛管压力与归一化湿相饱和度关系图（见图3）。由图3可知，毛管压力与归一化湿相饱和度并非呈线性关系。岩样1至岩样5，渗透率、孔隙度逐渐降低，物性变差，曲线弧度变大，岩样5甚至在整个孔隙半径区间上为一个光滑上凸曲线，因此Brooks⁃Corey法不适用致密砂岩储层孔隙结构分形特征的表征。

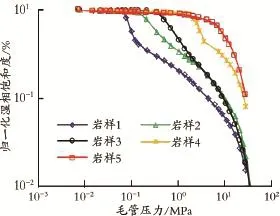
图3 毛管压力与归一化湿相饱和度关系Fig.3 Relationship between capillary pressure and normalized wetting phase saturation

根据式（7）作5块岩样毛管压力与湿相饱和度关系图（见图4）。由图4可知，毛管压力与湿相饱和度并不完全呈线性关系，岩样物性越差，线性段长度越短。如岩样1渗透率最高，则直线段最长，而岩样5渗透率最小，则其直线段最短。根据图4可以预测，当储层物性进一步改善，对于中高渗砂岩储层，直线段长度会延伸至整个孔隙半径区间；对于物性更差的储层，直线段可能会持续缩短直至完全变为曲线。因此贺成祖法不适用于物性较差的致密砂岩储层，而适用于物性较好的砂岩储层。

根据式（9）作5块岩样毛管压力与进汞饱和度关系图（见图5）。由图5可知，在毛管压力与进汞饱和度并不完全呈线性关系，岩样物性较差时为线性关系。如岩样4、5，渗透率、孔隙度较低，毛管压力与进汞饱和度呈线性关系；而岩样1、2、3物性相对较好，毛管压力与进汞饱和度不呈线性关系。因此Li Kewen法适用于物性较差的致密砂岩储层，而不适用于物性较好的砂岩储层。

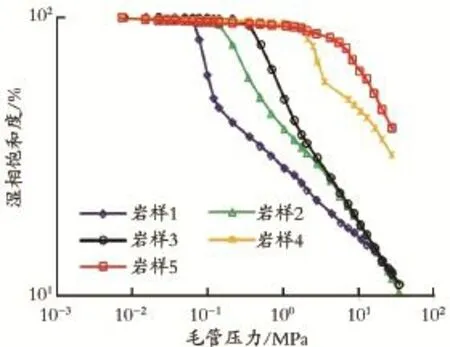
图4 毛管压力与湿相饱和度关系Fig.4 Relationship between capillary pressure and wetting phase satur ation

图5 毛管压力与进汞饱和度关系Fig.5 Relationship between capillary pressure and mercury entering in core samples phase saturation

为了进一步确定贺成祖法和Li Kewen法各自的适应性，选用刘晓鹏等[13]、刘刚等[14]、吴浩等[15]文献中鄂尔多斯盆地渗透率在（6.520～0.015）×10-3μm2的12组致密砂岩压汞曲线数据，根据式（7）、（9）处理压汞曲线数据分别得到毛管压力与湿相饱和度和进汞饱和度双对数曲线，如图6所示。由图6（a）可知，对于鄂尔多斯盆地致密砂岩，当渗透率大于0.1×10-3μm2时，毛管压力与湿相饱和度在对数坐标中呈线性关系，图6（a）中除右上方渗透率分别为 0.015×10-3、0.027×10-3μm2的 2 块岩样外均为线性关系，这与图4结果一致，表明贺成祖法适用于渗透率大于0.1×10-3μm2的致密砂岩储层。由图6（b）可知，当渗透率小于0.1×10-3μm2时，毛管压力与进汞饱和度在对数坐标中呈线性关系，即图6（b）中只有渗透率为 0.015×10-3、0.027×10-3μm2的 2块岩样为线性关系，这与图5结果一致，表明Li Kewen法适用于渗透率小于0.1×10-3μm2的致密砂岩储层。因此，本文数据和鄂尔多斯盆地数据均表明，以0.1×10-3μm2为界，贺成祖法适用于渗透率大于0.1×10-3μm2的致密砂岩储层，而Li Kewen法适用于渗透率小于0.1×10-3μm2的致密砂岩储层。

图6 贺成祖法和Li Kewen法适用性分析Fig.6 The analysis of the feasibility of He Chengzu method and Li Kewen method

3.2 分形区间

由分形定义法可知（见图2），致密砂岩储层在整个孔隙半径区间上具有分形特征。而所谓的分段分形特征，是由于孔隙结构分形特征表征方法选择不当导致的。采用Brooks⁃Corey法研究5块岩样的分形特征可知，各岩样至少具有3个以上的分形区间，尤其对于岩样5，甚至具有5个分形区间（见图3）；采用贺成祖法，则各岩样具有2个分形区间，且各岩样分形区间界限不同，表明分形区间与孔隙大小并没有直接关系，而是单纯的方法不当导致的；如果采用Li Kewen法，则岩样1、2和3具有3个分形区间，而岩样4和5可认为只有1个分形区间。

3.3 分形维数

利用分形定义法，根据式（1）计算岩样分形维数，根据压汞数据计算岩样平均孔隙半径、排驱压力、束缚水饱和度等参数，结果见表1。由表1可知，5块致密砂岩岩样分形维数分布在2.76～2.97，且分形维数越大，岩样物性越差，平均孔隙半径越小，排驱压力越大，束缚水饱和度越大，表明分形维数能够表征储层条件好坏，是储层评价的重要参数。例如，岩样1的分形维数最小为2.76，其渗透率和孔隙度最大，物性条件较好，排驱压力仅为0.04 MPa，平均孔隙半径较大为9.79 nm，束缚水饱和度仅为8.4%，这均表明5块岩样中岩样1储层物性最好，为开发有利储层；而岩样5的分形维数高达2.97，其渗透率仅为0.04×10-3μm2，平均孔隙半径仅为6.70 nm，物性条件极差，排驱压力高达0.92 MPa，束缚水饱和度高达33.1%，表明岩样5储层物性最差。

4 结 论

（1）分形定义法能够有效表征致密砂岩孔隙结构分形特征，贺成祖法适用于渗透率大于0.1×10-3μm2的致密砂岩储层，Li Kewen法适用于渗透率小于 0.1×10-3μm2的致密储层，而 Brooks⁃Corey法完全不适用于致密砂岩储层。

（2）致密砂岩储层在整个孔隙半径区间上具有分形特征。而所谓的分段分形特征，是由于孔隙结构分形特征表征方法选择不当导致的。

（3）分形维数是储层评价的重要参数，分形维数越大，储层物性越差，平均孔隙半径越小，排驱压力越大，束缚水饱和度越大。