基于ANSYS的埋地套管力学分析
2019-04-29李自力周嘉瑜王一舒
郭 健,李自力,李 扬,崔 淦,周嘉瑜,王一舒
(中国石油大学(华东)储运与建筑工程学院,山东青岛266580)
穿越公路或铁路的埋地油气管道有两种基本形式:有套管或无套管穿越。油气套管特别是长输套管,承受的内压较高,加上公路或铁路下的埋地套管所承受的土壤重量和车辆荷载又相当大,在无高性能的厚壁钢管以及工业技术整体水平还不高的年代,有套管穿越几乎成了唯一的方式。有套管的结构从受力上来看,是较合理的,套管承受土壤自身产生的压力和附加车辆载荷,输送管主要承担输送介质的内压[1]。
目前,国内外对交通载荷下埋地管道的力学分析作了大量的研究,但对油气管道的套管力学分析研究不多。由于套管钢材的强度远高于地层,所以当上覆岩层的压力转嫁到套管上时,套管体受到很大的压缩应力,套管体局部变形,产生应力集中,使得套管受到极大的应力作用。随着地层的变形套管亦会产生形变,且地层变形量越大,套管变形越明显,严重时引起套管损坏。压实过程会产生诸多危害,并且会伴随着油气的输送而更加显著的表现出来[2]。20世纪70年代,Winker提出了弹性地基梁的概念[3],后来被引入到管土相互作用的研究中。张坤勇等[4]在Winkler经典解答基础上,给出了一种适用于描述任意位移荷载条件下管线的解析解。王小龙等[5]基于Winkler假设的弹性地基梁理论,建立了埋地钢管在局部悬空时管道与土相互作用的力学模型。上述模型存在大量简化,且不能较好地模拟管土间的非线性摩擦。本文主要基于ANSYS有限元软件,对油田常见的几种容易产生破坏的集输管道套管建立了三维有限元模型,分析了套管达到屈服强度后的地面所需要施加的载荷大小,研究结果可为管道与套管的安全防护提供一定的参考[5]。
1 套管三维有限元模型建立
1.1 材料模型及单元选择
石油套管的钢级有:H40、J55、K55、N80、L80、C90、T 95、P110、Q125、V 150等。其中,J55为常用的石油套管钢材,其本构采用Ramberg⁃Osgoosd模型,其表达式为[6⁃7]:
其中:

式中,ε(σ)为管材总应变;σ为管材总应力,MPa;E为管材弹性模量,GPa;σR为 Ramberg⁃Osgoosd应力,MPa;n为管材的硬化系数。
土体本构采用Drucker⁃Prager模型,其表达式为[8⁃9] :
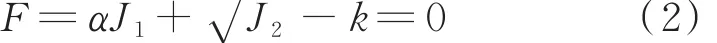
其中:
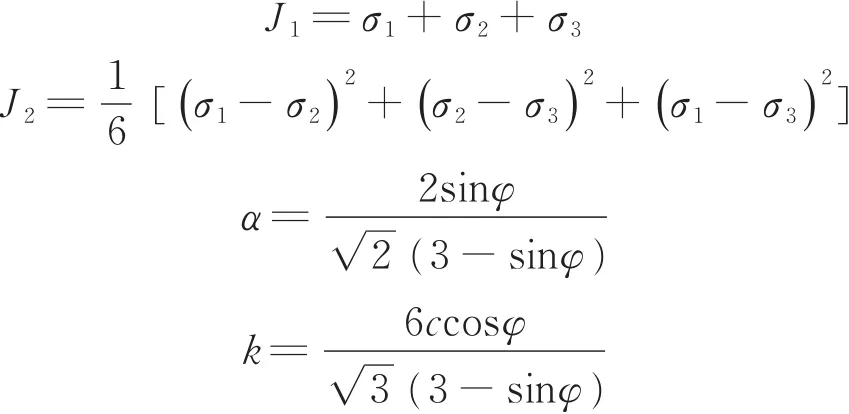
式中,F为屈服函数,J1为应力张量第一不变量,J2为应力张量第二不变量;σ1、σ2、σ3分别为第一、第二、第三主应力,MPa;α和k为正的材料常数,c为土体黏聚力,kPa,φ为内摩擦角,(°)。套管与土体材料参数取值如表1所示。

表1 套管与土体材料参数Table 1 Casing and soil material parameters
套管和土体单元均选择SOLID95。SOLID95是比3D8节点固体单元SOLID45更高级的单元。它能够吸收不规则形状的单元而精度没有损失。SOLID95单元有可并立的位移形状并且对于曲线边界的模型能很好的适应。单元由20个节点定义,每个节点有3个自由度:在节点x、y、z方向的平移。单元可能有任何的3D方位。SOLID95有塑性、蠕变、应力刚度、大变形以及大应变能力[10⁃11]。
套管与土体间采用面⁃面接触方式,接触单元选择 CONTA 174,目标单元选择 TARGE170。CONTA 174为3D8节点面面接触单元,可描述3D目标面(TARGE170单元)同该单元所定义的变形面间的接触和滑移状态,支持库仑和剪应力摩擦[12]。
1.2 网格划分与边界加载
套管和土体均采用六面体网格划分[13],如图1所示。
由于土体刚度明显较套管小,因此选择套管外壁为目标面,对应的土体表面为接触面,并分布在2个表面上创建目标单元与接触单元,构成接触对[14],如图2所示。模型底面为固定约束,上表面为自由面,土体边界约束水平方向,套管两端施加全约束。
1.3 计算模型的简化
由于管土模型沿横向与纵向对称,所以在计算套管和土壤接触分析时,把原来的复杂模型进行简化。在模型中心处沿横向与纵向分别切分,对四分之一模型进行求解,如图3所示。
从图3可以看到,红色部分为载荷施加区域,为使计算结果更加精确,在载荷施加区域做了局部网格的细化[15]。
网格划分时,增加网格数量可以使计算精度提高,但会增加计算时间。当网格数量增加到一定程度后,再继续增加网格时技术精度提高甚微。经过网格收敛性分析,本文模型的最优网格数量为19 840。

图1 网格划分Fig.1 Grid partition

图2 管土接触对Fig.2 Pipe and soil contact

图3 切分后套管与土壤接触模型立体图Fig.3 Stereoscopic model of contact between casing and soil after dicing
2 模型可靠性室内实验验证
2.1 实验设计
ANSYS建模过程中进行了假设与简化,与实际情况可能存在误差,为验证模型的准确性,设计套管应力实验土箱,将相应尺寸套管埋设于土箱中,通过结构实验反力装置、千斤顶和荷载均布钢板加载荷载,并使用压力传感器记录附加荷载的变化;使用电阻应变片来测量套管的应变;从而实测得到套管在不同荷载作用下的应力变化情况。同时以所建模型来模拟实验条件工况,将实验结果与模拟结果进行对比,计算误差,验证模型准确性。
实验的加载装置采用300 kN微机控制反力架加载系统,主要由H型自平衡门式反力架、钢结构反力底座、力传感器、油管、螺栓等必要的附件组成,如图4所示。

图4 室内实验加载装置Fig.4 Indoor test loading device
实验中采用电阻应变片来测量套管的应变,电阻应变片型号为 BX120⁃3AA,精确等级为A,电阻为120.1±0.1Ω,灵敏系数为2.01±1%。应变片数据均由XL 2118A静态应变仪采集[16]。
实验套管直径为48 mm,壁厚为3.5 mm,管材为碳钢。用卷尺测量找出套管正中间位置,以其对应于荷载正下方,以套管中点截面为对称面,两边每30 cm处选取一个截面,一共选取7个截面,在每个截面的套管顶部、侧面以及底部粘贴应变片,具体位置如图5所示。

图5 实验管段和应变片粘贴位置Fig.5 Test pipe section and str ain gauge attachment position
2.2 结果验证
荷载从0开始施加,每10 k N记录一次数据,施加至100 kN,分别测量套管顶部、侧面以及底部的应变。由测试结果可知,管顶管底应变较大,管侧应变很小接近于0,故不作讨论。其中管顶压应变为负值,取绝对值作图,管底拉应变为正值。套管管中心截面管顶和管底应变如图6所示。由图6可知,套管中心应力与所施加载荷呈线性关系。

图6 套管管中心应变与荷载关系Fig.6 Casing center strain and load relationship
分别取载荷50、80、100 k N时的套管沿线顶部以及底部应变测量结果与模拟结果进行对比,结果如图7所示。由图7可见,测量结果与模拟结果的曲线稳合。


图7 不同载荷下套管不同位置的应变对比Fig.7 Strain comparison of different positions of casing under different loads
由于套管中间位置受力最大,故产生最大的应变,为最危险位置,在三个载荷下计算该位置的模拟值与测量值的相对误差,结果如表2所示,相对误差不超过10%。由于套管和土壤的复杂性,任何方法都不能得到准确的结果,一般在工程中误差20%以下都在可应用的范围内。因此,该模型基本满足实际计算需要,用来进行数值计算及仿真,可以省却很多人力、物力和时间。
3 套管力学分析实例
套管通常采用钢筋混凝土或者钢质套管。当套管直径大于1 000 mm时宜采用钢筋混凝土套管。套管的设计执行国家现行标准《铁路桥涵设计基本规范》TB10002-2017[17]或《公路桥涵设计通用规范》JTG D60[18]。套管直径要求比主套管直径至少大100 mm。
以东营市胜利油田为分析案例。经过调研,东营市的集输管道直径都在1 000 mm以下,所以一般选用钢制套管。模拟选取直径为159 mm的20#钢石油管道作为研究对象,20#钢屈服强度为234 MPa。套管直径要求比主管道直径至少大100 mm,壁厚不小于5.6 mm,因此套管按照上述要求,选取直径259 mm,壁厚5.6 mm的套管进行模拟。

表2 套管管中心应变模拟值与测量值比较Table 2 Casing center simulation value and measured value strain result comparison
由文献[17]可知,大型汽车轮压为0.7 MPa,当量接地尺寸为0.32 m×0.22 m。J55钢套管的屈服强度为379 MPa,强度极限为530 MPa,为使套管尽可能达到屈服强度,埋深取0.3 m。模拟结果如图8所示。
当套管达到屈服强度时,此时地面施加的临界载荷为2.3 MPa,为大车轮压的3倍多,此时套管最大位移为9.297 mm。根据文献[17]中4.4.3所述规律,如果继续加大埋深,套管最大应力会随之减小。因此,有套管保护的管道极难遭到破坏。
由上面分析可知,实际管道与套管一般不接触,在这种状态下,管道是非常安全的。但考虑到某些极端情况,管道顶端有可能与套管发生接触,如图9所示,套管对管道产生直接接触有可能对管道产生破坏。根据此类情况,在模拟中将管道与套管的接触形式设为线接触。
由于套管和管顶接触,使套管对土壤的支撑力增大,因此,当套管达到屈服强度时,此时地面施加的载荷临界值为3.9 MPa,为大车轮压的5倍多,此时管道应力为253 MPa,刚刚达到管道的屈服强度,如图10、11所示。在这种极端情况下,有套管保护的管道是难以达到破坏的。

图8 套管应力和位移云图Fig.8 Casing stress cloud and displacement cloud

图9 套管与管道顶部接触模型Fig.9 Casing and pipe top contact model

图10 套管与管道应力分布Fig.10 Casing and pipe stress distribution
东营市胜利油田的套管与管道还存在着如图12(a)的连接方式,即套管与管道两端焊接在一块的情况。根据此类情况,在模型中将套管与管道之间的接触形式设为固定接触。

图11 管道应力分布图Fig.11 Pipe stress distribution
当管道达到屈服应力时,此时地面施加的载荷临界值为1.6 MPa,为大车轮压的2.3倍多。套管与管道应力分布图如图12(b)所示。管道中部与套管不发生接触,因此套管对管道中部起到了保护作用,而焊接处会承受一定的拉应力,因此最大应力发生在管道与套管连接处,此处也最易受到破坏,应加强保护。

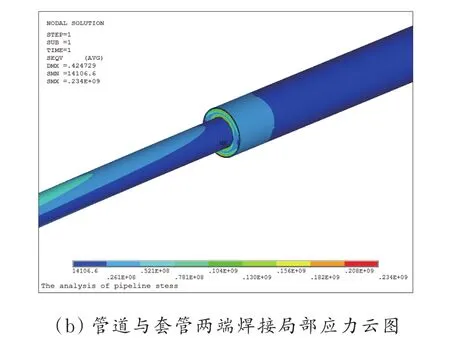
图12 管道与套管连接示意与两端焊接局部应力云图Fig.12 Welding part and local stress cloud diagram at both ends of pipe and casing
4 结 论
基于ANSYS建立了埋地套管的三维有限元模型,结合室内实验得出:
(1)在固定载荷下,套管应力分布由中心向两端减小;套管中心应力与所施加载荷呈线性关系。将试验结果与模拟结果进行对比,两者较为接近,验证了模型模拟结果的准确性,此模型可用于套管的安全评价分析。
(2)当管道顶部与套管接触,埋深取0.3 m,套管达到屈服强度时,地面施加的载荷临界值为3.9 MPa,为大车轮压的5倍多,此时管道应力为253 MPa,刚刚达到管道的屈服强度。在这种情况下,有套管保护的管道难以达到破坏。
(3)当套管两端与管道焊接在一起,埋深取0.3 m,管道达到屈服应力时,地面所施加的载荷临界值为1.6 MPa,为大车轮压的2.3倍多。由于套管中部与管道不发生接触,因此套管对管道中部起到了保护作用,而焊接处会承受一定的拉应力,因此最大应力发生在管道与套管连接处,此处最易受到破坏,应加强保护。
