多极双余度电磁铁特性分析

2019-04-28郎召伟孙芳芳

微电机 2019年3期

郎召伟，孙芳芳

(航空工业庆安集团有限公司，西安 710003)

0 引言

电磁制动器是飞行器上常用制动器之一，对安全性要求较高。而影响电磁制动器安全性能的最主要的结构是电磁铁。为提高电磁铁的可靠性，一般采用多余度设计，目前现有结构均是在电磁铁内部增加了线圈余度，几个余度的线圈同轴，且多个线圈的外径、内径和长度相等，仅通过改变线圈的轴向位置来实现多余度设计。但线圈位置不同，会造成几个线圈对动衔铁产生的吸力值不同，对设计提出了更高的要求。

本文中的多极双余度电磁铁在环形静衔铁圆周方向分布六个线圈骨架，骨架内侧是铁心，外侧是漆包线，六个线圈可以采用双余度或三余度方式[1]。目前这种多极双余度电磁铁在实际生产中没有应用，对其研究也较少，故本研究通过仿真对这种多极双余度电磁铁进行分析，探讨双余度电磁铁的不同线圈分布对电磁铁性能的影响。

1 结构原理

用于电磁制动器的多极双余度电磁铁的结构如图1所示，其结构由轴、动衔铁、壳体、铁心、骨架、线圈、静衔铁、弹簧压环、弹簧、轴承等组成。其中轴、动衔铁、铁心和静衔铁为导磁材料，壳体、骨架和弹簧压环为非导磁材料，线圈由漆包线缠绕而成。静衔铁固定在壳体上，动衔铁可在轴向方向自由移动，动衔铁的左侧安装有摩擦片。线圈断电时，在弹簧力的作用下，弹簧压环推动衔铁向左运动，压紧摩擦片，使轴制动，此时铁心与动衔铁之间的气隙为0.6 mm；线圈通电时，动衔铁在电磁吸力的作用下向右移动，释放摩擦片，则轴可转动。

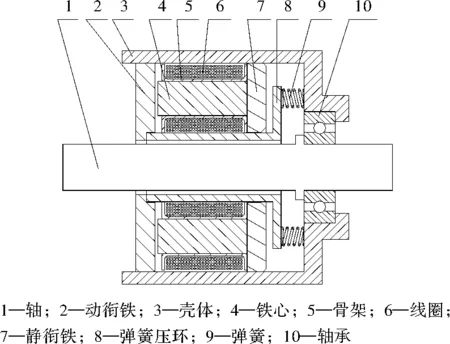
图1 多极双余度电磁铁结构示意图

图2 多极双余度电磁铁铁心和线圈分布图

多极双余度电磁铁铁心和线圈分布如图2所示，从图中可看出电磁铁有6个铁心和线圈，铁心呈环形固定在静衔铁上，骨架包围在铁心外侧，线圈缠绕在骨架上。双余度电磁铁需将6个铁心和线圈分为两组，每3个一组串联通电，下面探讨分组情况对电磁铁性能的影响。

2 仿真方法

由于本模型有6个沿环形分布的线圈，只能用3D进行仿真，使用Catia中建立模型，导入Ansoft/Maxwell中使用。由于壳体、骨架和弹簧压环为非导磁材料，在建模时可将其忽略，只建立轴、动衔铁、静衔铁、线圈和铁心。

本研究用Ansoft/Maxwell分别进行静态和瞬态分析，在进行瞬态分析时，原片状的动衔铁外圆柱面和内圆柱面需改为多棱柱面，band也为多棱柱面。模型导入后需设置模型的材料，建立轴、动衔铁、静衔铁和铁心定义为Steel 1008，铁心定义为copper，region和band均为vacuum[2-5]。在给线圈添加激励时添加外部电路，图3为外部电路电路图。图2中所示线圈等效为图3中的线圈和电阻，三个线圈串联。

图3 外部电路电路图

由于电磁铁在实际工作中动衔铁与壳体接触面较小，润滑比较好，因此在仿真过程中忽略动衔铁运动时的摩擦力，在motion中，动衔铁质量设置为0.844，弹簧力为200 N；网格划分时，采用自动划分网格，再将band和动衔铁等关键位置加密，最后添加求解设置，运行软件求解。

本研究只对多极双余度电磁铁的一个余度进行计算，即将其中3个线圈串联通电。通电方式分别为3组，第一组是图2中线圈1、2、3，第二组是线圈 1、2、4，第三组是线圈1、3、5，电路图如图3所示，通电电压为28 V，每个线圈的电阻为2.3 Ω。拿第一组为例进行说明，线圈1、2和3通电，线圈4、5和6不通电，磁力线从1、2和3的铁心到达动衔铁，穿过气隙和动衔铁到4、5和6的铁心，最终通过静衔铁回到1、2和3的铁心，形成回路。由于多极双余度电磁铁的4、5、6线圈通电与1、2、3通电完全相同，3、5、6通电与1、2、4完全相同，2、4、6通电和1、3、5通电完全相同，此处不再重复计算。

3 有限元计算结果及分析

图4为电磁力随时间的变化关系，图5为动衔铁位移随时间变化关系，图6为线圈1电流随时间变化关系，线圈2和线圈3电流变化趋势与线圈1基本一致。由图可知，电磁力和电流随时间逐渐增大，当电磁力到达0.2 kN时，电磁力将克服施加在动衔铁上的弹簧力，动衔铁开始向铁心方向运动，气隙减小，此时电磁力增加速度变快，而电流却减小，当动衔铁运动到终点位置时，不再运动，而电流和电磁力继续增大。

通电后，电流的变化趋势是由于线圈中不仅有电阻，还有一定的电感值，所以电流的上升不能立即达到稳定值，而是按照指数曲线的规律逐渐上升。当电流增长到一定数值时，磁通也相应地增长到一定值，当磁铁所产生的电磁吸力足以使得动衔铁开始运动，气隙减小，气隙中磁阻改变，使线圈中电感发生变化，引起一个反电动势，如式(1)所示，使得线圈中电流减小[6]。当衔铁达到终点位置而停止运动时，气隙不再变化，电感值也不再改变，这项反电动势消失，这时电流和磁通又继续上升至稳定值[7]。

(1)

式中，E为电动势；i为电流；L为电感；t为时间。

电磁力在动衔铁运动之前上升是由于电流随时间上升，磁通是由电流的激励所产生的，所以磁通增长的规律和电流相同，由式(2)可看出电磁力随着磁通的增长而增长。而当动衔铁开始运动时，电流有所下降，而电磁力却上升。这是由于电磁铁运动时，气隙δ不断减小，根据式(3)可知，气隙磁导随着气隙长度的减小而增大。磁通Φ随着气隙磁导的增大而增大，因此电磁力增大。当动衔铁运动到终点位置时，气隙δ不再变化，电磁吸力随着电流的增长而增长。

(2)

式中，Φ为气隙中磁通(Wb)；S为磁极端面处截面积(m2)；μ0为空气导磁率(Wb/A×m)。

(3)

式中，G0为气隙磁导(H)；μ0为空气导磁率(Wb/A×m)；s为截面积(m2)；δ为气隙长度(m)。

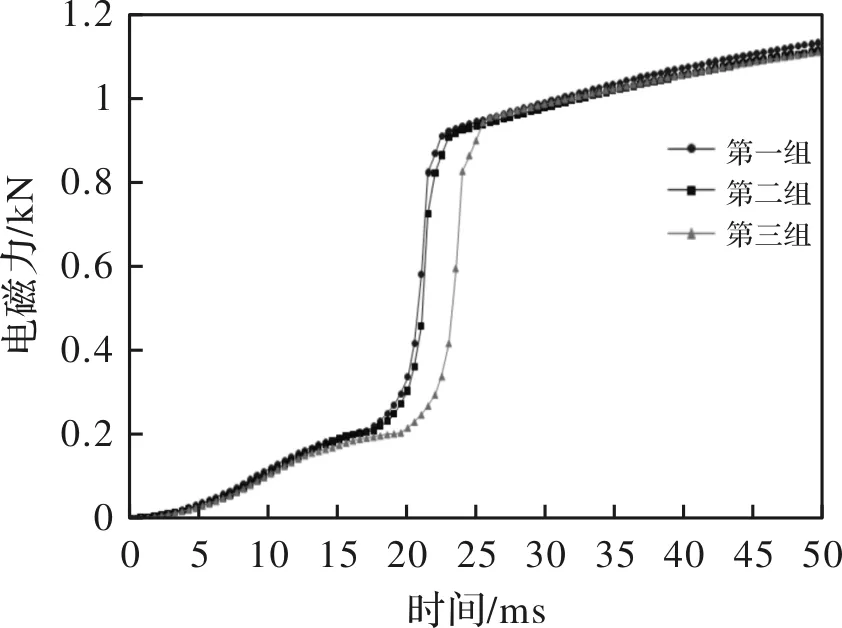
图4 电磁力随时间的变化关系

图5 动衔铁位移随时间变化关系

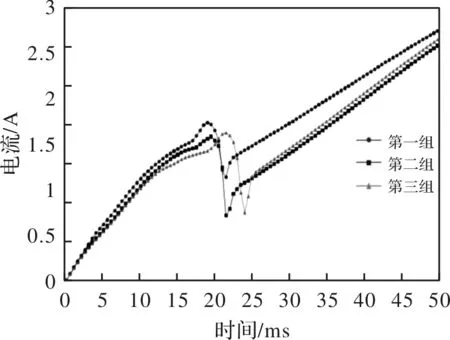
图6 线圈1电流随时间变化关系

表1为T=0.015 s时电磁力和电流及电磁铁吸合时间，从表1中可看出，在动衔铁吸合之前，T=0.015 s时，第一组电磁力最大，为190 N；第二组次之，为189 N；第三组最小，为174 N；T=0.015 s，第一组的电流最大，为1.45 A；第二组次之，为1.38 A；第三组最小，为1.31 A；第一组的动衔铁最先吸合，用时21.5 ms，第二组次之，用时22 ms，第三组动衔铁最后吸合，用时24 ms。

表1 T=0.015 s时电磁力和电流及电磁铁吸合时间

第一组的电流最大是由于第一组线圈的电感量最小，图7为静态仿真电感量，3个线圈串联后，总电感等于3个线圈的自感和互感之和[8]，计算可得第一组的总电感量为98.25 mH，第二组为103.12 mH，第三组为103.65 mH。由式(4)可知，由于三组线圈的电阻R和电压E相等，L越小，电流增长越快，导致电磁力也增长最快，最终使吸合时间最短。

(4)

式中，E为电压；R为电阻；L为电感；t为时间。

图8为T=0.015 s时电磁铁瞬态磁场[9]，T=0.015 s时动衔铁还未开始运动。从图中也可看出，第一组线圈产生的磁场强度大于第二组，大于第三组，根据式(5)可知，电磁力与磁场强度的平方成正比，磁场强度大，则电磁力大。因此第一组的电磁力最大，吸合时间也最短。

(5)

式中，F为电磁吸力(F)；B为磁场强度(T)；S为磁极表面的总面积(m2)；μ0为空气磁导率(Wb/A×m)。