永磁同步电机速度伺服系统的复合有限时间控制

陈 哲，王逸衍，刘春强，骆光照，刘卫国

(西北工业大学 自动化学院电气工程系，西安 710072)

0 引 言

永磁同步电机具有结构简单、体积小、转矩惯量比高、可靠性好、伺服性能优良等优点，在航空航天、医疗器械、数控机床等领域被广泛地应用[1]。现如今，大部分的永磁同步电机调速控制常采用经典控制理论，如PI控制，这种线性控制方法算法简单、可靠性高，通常在参数匹配的情况下可取得较好的控制性能。然而，永磁同步电机是一种典型的非线性强耦合系统，特别是作为伺服电机在运行过程中，转动惯量等参数摄动以及外部负载力矩、不确定的外部干扰使PI控制难以满足高性能的控制需求。要实现高性能伺服控制，就必须克服这些因素对系统带来的不利影响。

近年来，随着先进控制理论的提出和完善，各种非线性控制方法得到了进一步发展。基于现代控制理论指导下的有限时间控制方法，可以使系统状态在有限时间内收敛至平衡点，从而提升系统的鲁棒性和抗扰动性能，受到了广泛关注。对于一阶、二阶系统，常采用齐次性方法[1～3]、加幂积分法[4]和非奇异终端滑模法[5,6]等设计其有限时间控制器。文献[1]利用反步构造法为永磁同步电机位置伺服系统的位置环设计了一种基于加幂积分法和反馈线性化的有限时间控制器。利用有限时间Lyaponov稳定性理论证明了误差收敛域和控制器参数的关系。和基于PD控制器的方法相比，这种控制策略提升了系统对负载扰动的鲁棒性。文献[4]为永磁同步电机调速系统的速度环设计了一种基于齐次性方法的有限时间控制器，并结合扰动观测器实时观测系统扰动并在前馈通道上进行补偿。该复合控制策略可以提高系统的抗干扰性能。文献[5]为永磁同步电机调速系统的速度环、直轴电流环和交轴电流环分别设计了二阶终端滑模控制器，使得系统误差可以在有限时间内收敛至平衡点。这种控制策略提升了系统对负载扰动的鲁棒性且避免了抖振。

其中，基于齐次性方法设计的有限时间控制器，控制性能优越，结构较为简单，待定参数少。在实际应用中，系统中总是存在不确定的扰动，且扰动模型难以准确建立。韩京清研究员提出的扩张状态观测器[7]不依赖精准模型的建立，可实时观测出系统的不确定性扰动，将其扩张成系统状态。

本文结合齐次有限时间控制和扩张状态观测器的优点，为永磁同步电机速度伺服系统的速度环、电流环提出了基于有限时间反馈控制和扩张状态观测器前馈补偿的复合控制策略。该方法可实现转速误差、电流误差的快速收敛，进一步提升系统的抗干扰性能。仿真结果验证了该方法的有效性。

1 永磁同步电机的矢量控制

1.1 永磁同步电机的数学模型

本文以表贴式永磁同步电机为研究对象，建立了PMSM在d-q轴旋转坐标系下的理想数学模型。

定子电压方程为

(1)

式中，ud、uq为定子电压d-q轴的分量，id、iq为定子电流d-q轴的分量，Ld、Lq为d-q轴的等效电感，ωe为电角速度，ψf为永磁体磁链。

电机的机械运动方程为

(2)

式中，ωn为电机的机械角速度，J为转动惯量，TL为负载转矩，B为阻尼系数。

电机的电磁转矩方程为

(3)

式中，Te为电机的电磁转矩，np为电机极对数。

对于表贴式电机，有Ld≈Lq=Ls，则上式可简化为

(4)

式中，Kt为电机的转矩常数。

1.2 基于有限时间控制的速度伺服系统

为实现电流的近似解耦，设定id的参考量为零。考虑到有限时间控制技术可以提高系统误差的收敛速度，为提升系统的抗扰动性能，本文为永磁同步电机速度伺服系统的速度环、电流环分别设计了基于有限时间技术和扩张状态观测器的复合控制器。基于有限时间收敛控制的系统框图如图1所示。

图1 基于有限时间收敛控制的系统框图

2 复合有限时间控制器设计

传统PI控制下的闭环系统，PI参数的设计依赖于系统精准的建模。然而，电机运行时参数时变，高速运行时耦合情况加重，再有负载突变等种种因素，给系统带来了不确定的扰动，PI控制难以满足系统高性能的控制需求。

为改善系统的抗扰性，本文为永磁同步电机速度伺服系统的速度环和电流环设计了有限时间复合控制器。该控制器由位于前向通道的有限时间控制器(Finite Time Controller, FTC)和扩张状态观测器(Extended State Observer, ESO)等两部分组成。FTC通过分数指数幂的作用使误差在有限时间内快速收敛至平衡点，ESO实时观测出系统的不确定扰动，并将其视为系统总扰动补偿到输入端，进而提升系统的抗扰动性能。

2.1 速度环的有限时间控制

根据式(2)，电机的机械运动方程可改写为

(5)

令

(6)

则有

(7)

由此，可得永磁同步电机速度误差系统一阶状态方程：

(8)

式中，ωr为电机给定转速的弧度值，es为给定转速与反馈转速间的误差。

对一阶系统(8)设计齐次有限时间控制器，控制器形式如下：

us=-kssign(es)|es|as

(9)

式中，us为速度环有限时间控制器的输出，ks为比例增益的大小，αs为分数指数幂，满足0<αs<1。

(10)

(11)

综合以上分析，设计如图2所示的速度环复合控制器，可以得到速度环的控制量输出如下：

(12)

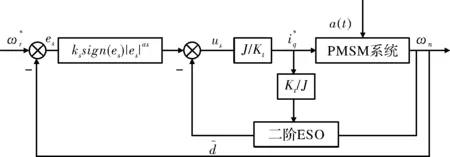
图2 速度环复合控制器结构框图

2.2 电流环的有限时间控制

为改善电流环的动态调节响应和抗干扰性能，可在电流环引入有限时间复合控制器，构造PMSM的双环有限时间控制器。

电流环的状态方程为

(13)

系统扰动量和控制量系数可按以下方程匹配：

(14)

(15)

可得d-q轴电流二阶线性状态扩张观测器的状态方程为

(16)

为使一阶电流误差系统在有限时间内镇定到原点，设计形式如下的齐次有限时间控制器：

(17)

式中，ed、eq分别为d-q轴参考电流与反馈电流间的误差，ki为比例增益的大小，αi为分数指数幂，满足0<αi<1。

(18)

图3 电流环复合控制器结构框图

3 仿真验证

为了验证复合有限时间控制策略的优越性，本文基于Matlab/Simulink平台对该方法进行了仿真验证，仿真所用的电机参数如表1所示。

表1 仿真所用电机参数

为减少电机起动过程中尖峰电流对开关管的冲击，为电机设计三段式S曲线转速规划，给定转速经加速-匀速-减速段后在0.6 s达额定转速2000 r/min。起动过程中，复合有限时间控制与PI控制的转速n和q轴参考电流的对比波形，如图4所示：

图4 空载起动时的复合有限时间控制与PI动态响应对比

图4表明，复合有限时间控制下的系统具有更加平稳和快速的动态响应性能。

在1.001 s时突加10 N·m的负载转矩，在1.501 s时突撤10 N·m的负载转矩，复合有限时间控制与PI控制的转速n和q轴电流参考值的对比波形，如图5所示。

图5 负载突变时的响应曲线

图5中可以看出，系统发生扰动后，复合有限时间控制下的系统，电机转速n只有4 r/min的小幅度跌落，且仅在0.008 s内迅速恢复至额定转速。较之于PI控制下的无限时间收敛系统，有限时间控制系统在时间上具有更优的收敛性，符合理论分析。

从式(15)、式(16)可知，控制器系数与电感参数Ls有关。现分析复合有限时间控制系统在电机电感参数摄动情形下的抗扰动性能。当电机电感参数分别变为原参数值的50%、200%时，在负载突变情形下的q轴电流响应曲线如图6所示。

图6 电感参数摄动时复合有限时间控制与PI响应对比

图6表明，在电感参数具有较大偏移量的情形下，在突加撤载时，有限时间复合控制器作用下的系统仍能实现q轴电流与转速的快速调节，系统表现出很好的抗参数扰动的性能。

可见，双环有限时间控制策略能在发生扰动的情况下使系统误差在有限的时间内快速收敛，增强了系统的抗扰动性能。

4 结 论

为提升永磁同步电机速度伺服系统的抗扰动能力，本文结合有限时间控制技术和扩张状态观测器，分别为系统的转速环、电流环设计了基于有限时间反馈控制和扩张状态观测器前馈补偿的复合控制器。

在Matlab/Simulink仿真平台中搭建了基于有限时间复合控制器的仿真模型，仿真结果证明了有限时间控制策略的有效性。