冷链物流中预冷技术研发投资微分博弈分析

孙冬石，于绍政，李浩渊 （大连东软信息学院，辽宁 大连 116023）

0 引 言

生活水平的不断提高，使人们对产品质量和安全问题的关注度不断上升。特别是生鲜产品，人们对其生鲜度有着很高的要求。对于产品保鲜的方法，一是在生产中提升，从供应源保证产品的质量；二是在物流过程中加强产品的监督，保证产品在消费之前始终处于冷链的过程中。随着供应链理论的发展，产品生产企业已经认识到了第三方物流的重要性，加之冷链物流自建的高投资，使越来越多的企业选择进行物流外包，并得到了较好的成效。但中间物流环节专业性却不能解决产品供应源头的质量问题，生鲜产品易腐性高的特色，让其有可能在未进入物流环节的时候质量就发生了变化。

解决这一问题的关键在于生鲜产品的供应商是否有意识进行产品质量控制，预冷技术为企业提供了解决方案。但生鲜产品供应商也面临这样的问题，预冷技术研发和适用前期投入大，其对企业利润的提升并无明显的改善，甚至很多供应商认为只要在把产品转移到冷链物流服务商手中的时候产品没有发生变质，就不需要进行预冷处理，那样只是额外增加企业运营成本。本文的研究将通过微分博弈的方法研究生鲜产品供应商采用预冷技术对企业长期发展的影响。

现阶段，学者们已经意识到预冷技术的重要作用，潘仟仟和张宁[1]等对国内外预冷技术在果蔬冷链物流中的应用进行了综述，发现在国外预冷技术的使用已经非常普遍，而我国3.8%的使用率说明预冷技术的开发空间很大；李腾[2]等在服务供应链视角下证明了预冷技术可以有效地抑制生鲜果蔬物流过程中的不确定因素；王想[3]等证明了生鲜产品的生鲜度是随时间变化的参数，再无外界因素影响下随时间递减，但却可以在资本投入、技术革新等影响下提高对时间的耐受性。

应该看到的是，阻碍我国冷链物流中预冷技术的实施主要并不在技术方面，企业前期投入与后期收益之间的不平衡是更重要的因素。目前，对于生鲜度这类随时间变化的对象进行控制研究的方法主要是建立时间状态方程，对影响状态方程的因素进行分析。在类似的研究中，陈树桢[4]等分析了商誉的变化与时间和广告投入之间的关系，建立了两级供应链模型，并通过灵敏度分析，求解广告投入的最佳决策；宋焕[5]研究新产品的开发过程中，供应商各环节主客体之间的投资策略，利用演化博弈模型，对企业在合作投资和不合作两种情况下的最终收益的变化进行分析，证明了下游企业在一定的阈值内有强意愿参与上游产品开发，通过供应契约下合作可能实现双赢；Chutan等[6]研究了在合作伙伴关系中，当无监管的情况下，产品质量随时间降低的现象，并对四种信息分享状态下，利用惩罚机制对缺陷产品进行质量监督的机制进行了分析；Jorgensen[7]在Nerlove的研究成果上进行了优化，构建了生产商为主导的供应链中促销策略的设计模型；Xie和Zhao[8]对碳排放敏感的供应链进行了研究，证明了供应商利益个体之间联合减排研发和进行低碳宣传是有效提升供应链效率的方法。

上述的研究表明，企业已经意识到预冷技术对冷链物流和生鲜产品品质的重要作用，但在实践的操作中，对预冷技术研发收入的费用分担问题还存在理论上的空白，目前的主流做法是生鲜品供应商或冷链物流商包干制，这样的方式对非长期合作的对象来说，会阻碍预冷技术的实施。所以，通过科学的方法制定预冷技术投入分配机制是提升生鲜产品供应链整体效率的重要途径。

1 模型描述

本文建立了一个生鲜产品供应商和一个零售商之间的二级供应链，产品供应商使用了预冷技术，并在产品的销售过程中进行了宣传，理性消费者将对使用预冷技术的产品有积极的反馈，为评价预冷技术投入的影响因素，进行如下假设。

假设1：供应商通过预冷技术研发可以提高产品的生鲜度。但产品生鲜度随着时间的推移会有自然衰减的现象，产品的生鲜度随时间变化的情况为：

假设2：消费者倾向于选择使用了预冷技术、生鲜度高、价格低廉的产品。市场需求的影响因素包含价格和非价格因素，借鉴Jorgensen和Zaccour[9]的研究成果，需求量为两者的可分离乘法函数：

假设3：根据众学者的研究成果，供应商实施预冷技术的成本为研发努力水平的凸函数：

其中：C为供应商研发或实施预冷技术成本，K＞0为预冷技术研发的努力水平对成本的相关系数。

假设4：供应商和零售商都为理性决策人，供应链上的库存成本和缺货成本为0，在较长的运营时间内，供应商和零售商的贴现率都为ρ（ ρ＞0），供应商给零售商的批发价为ω。则供应商、零售商和供应链的长期收益分别为：

2 模型求解与分析

2.1 竞争型决策

在这种情况，供应商和零售商之间进行Stackelberg博弈，假设供应链的主导者为生鲜产品供应商，则博弈顺序为：供应商优先确认研发预冷技术的努力水平和批发价，零售商据此确定零售价格，双方都为理性博弈人，追求利润最大，根据式（4）和式（5），长期收益函数分别为（为书写方便，所有与t相关的值省略）：

记在t时刻以后，供应商和零售商的长期利润最优价值函数可表示为根据最优控制理论，和）对任意E≥0都满足HJB方程，即：

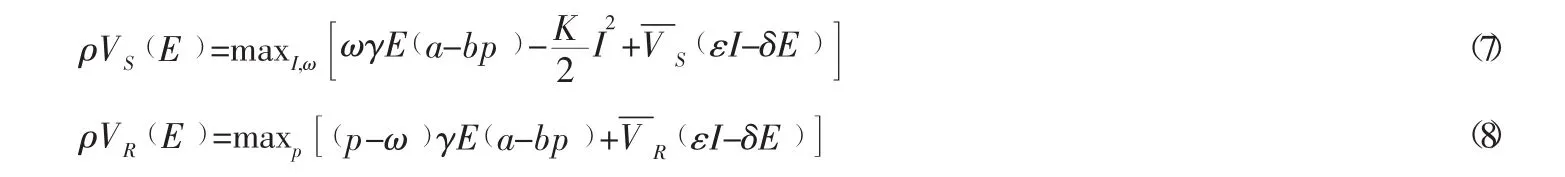
为了求出在竞争模式下的p和I，应用逆向归纳法，对式（8）右端对p求导，并令导数等于零，可得把p*带入式（7），并对I和ω求偏导，令偏导数等于零，可得把p*,I*,ω*带入式 （7） 和式 （8），整理得：

将以上最优策略代入状态方程式（1）得：

竞争模型下，把最优策略p*,I*,ω*和最优轨迹带入式（7） 和式（8），可得供应链的最优价值函数：

2.2 合作型决策

在这种模式下双方不以追求自身利润最大为目标，而是以供应链联合收益最大化为目标，通过收益共享契约等形式进行利润分配。根据式（6），且目标函数对任意E≥0同样满足HJB方程，可得：

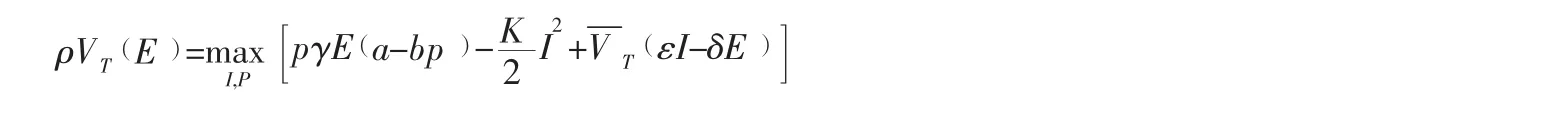
其最优策略p**,I**的求解过程同竞争型决策，由于篇幅有限，计算过程省略，得式（15）。

合作模式下，产品生鲜度E（t）的最优轨迹为（Z取值同竞争模式）：

合作模式下，供应链的最优价值为：

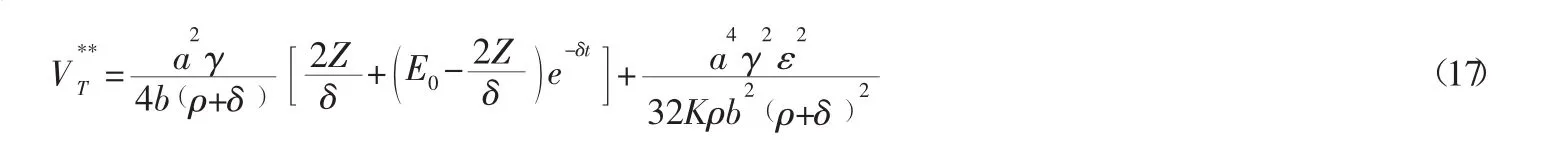
2.3 对比与分析

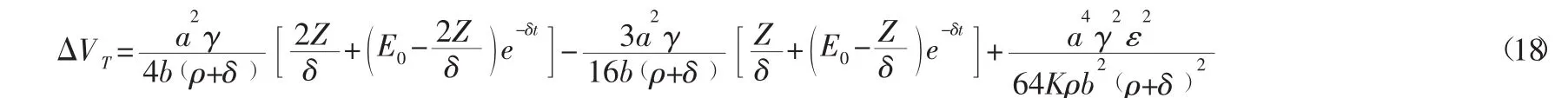
结论1：在合作型决策中，供应链的最优价值要相比竞争型决策中有所提高。这证明了通过收入共享契约，供应商和零售商能达成更好的合作，由于合作模型下双方之间流通成本和交易成本为0，投入和产出的分配比率就可以通过协商进行制定，这将有助于预冷技术投入的增加，是制定更好地投入分配模式的前提。

设 ΔI=I**-I*,Δp=p**-p*，由式 （11） 和式 （15），可得式 （19）：

结论2：因为a＞0，b＞0，则Δp＜0。与竞争模式相比，合作模式下虽然产品售价降低，但由于在结论1中证明了供应链价值提高，则该模式下生鲜产品的销售量增长率要大于价格的降低率，更多的产品进行流通的环节，使预冷技术的应用变得愈发的重要。而由式（19）可得ΔI＞0，证明在合作模式下产品供应商的确提升了预冷技术的投入，由于该项投入并无强制性，所以是供应商的自愿投入。这说明，在合作模式中，供应商由订单敏感，变成了实际需求敏感，更加关注消费者的满意度，愿意为提升供应链整体价值努力，形成良性的循环。

3 模拟分析

为验证上一部分结论，并分析某些重要参数变化对生鲜产品供应商对预冷技术的努力程度的影响，本部分根据Giovanni[10]的研究成果，进行参数设置和敏感度分析。基准参数设置为：a=5，b=1，ω=2，γ=0.5，ε=0.8，δ=0.2，ρ=0.3，K=1，E0=10。

首先，根据式（13） 和式（16），按照预设参数分别绘制竞争型决策和合作型决策中生鲜度E（t）的最优轨迹E（t）*和E（t）**，取 t∈ [0,30]。然后，分别选取对预冷技术研发的努力水平I有重要影响的消费者生鲜度敏感系数γ和消费者价格敏感系数b，根据式（11） 和式（15），保持其他因素不变的前提下，分别取γ∈[0,10 ]，b∈ [0,3]，绘制两种情况下I的变化情况，如图1所示。

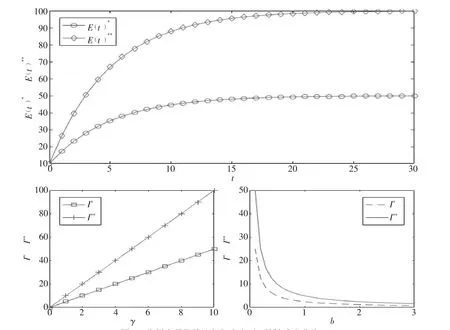
图1 生鲜度最优轨迹与努力水平I的敏感度曲线

由最优轨迹的图形可以看出，在合作型决策中，随着时间变化，生鲜度一直处于比竞争模式高的水平。综上生鲜度的动态方程，可知在合作型决策中，供应商进行了对预冷技术额外的研发投入，与理论推导结论一致。

努力水平I在单独被消费者生鲜度敏感系数γ影响时，I与γ呈线性正相关的关系。且在合作型决策下，消费者的生鲜敏感度将对I产生更大的影响。这是由于合作型决策下，供应商和零售商的收益是共享的，其共同的关注点是终端消费者的购买量。当消费者对生鲜度要求较高，供应链上的企业都有意愿进行改进。而竞争型决策中，供应商对终端消费者关注不足，其只关注下游零售商的订单量。关注点的不同，将导致对预冷技术投入的不同。

努力水平I在单独被消费者价格敏感系数b影响时，I的曲线为单调递减函数。这说明随着消费者对价格敏感度提高，供应商进行预冷研发的意愿会降低，因为如果研发导致价格上升，将使消费者需求量下降，供应商利润随之下降；如果价格不变，产品成本将增加，供应商的利润也会下降。但也能看出，在合作型决策下，I**的曲线始终在竞争型决策下I*的曲线的上方，这说明在相同的敏感度下，合作型决策下供应商对提升预冷技术的意愿更强烈，一方面，是由于供应商希望通过提升消费者满意度提高销量；另一方面，在于预冷技术的投入也可以由零售商共同承担。

4 结论

本文建立生鲜度状态方程，并应用微分博弈的方法分别对合作型决策和竞争型决策两种情况下供应商对预冷技术研发投入进行了分析。证明了在合作型决策中，预冷技术将被更广泛的使用，且消费者也能享受更低的商品价格，供应链的整体收益将得到提升，实现“双重帕累托优化”。