基于车桥耦合的三跨连续拱梁组合桥冲击系数研究

朱劲松，徐余锋



基于车桥耦合的三跨连续拱梁组合桥冲击系数研究

朱劲松1, 2，徐余锋1

(1. 天津大学 建筑工程学院，天津 300072； 2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072)

为合理分析和计算桥梁结构各关键部位的冲击系数，以三跨连续拱梁组合桥为例进行分析。分别利用MATLAB和ANSYS建立11自由度的三维车模型和有限元模型。采用车桥耦合迭代的方法，得到桥梁关键部位在车辆荷载作用下的振动响应。研究结果表明：车辆在任何车道行驶时，边主梁、边拱肋及斜吊杆的冲击系数都大于相应中主梁、中拱肋及直吊杆；随着桥面平整度等级的增加，各关键部位的冲击系数与振动系数的关系满足均幂函数，且呈非线性增长；随着车速的增加，车辆在不同车道行驶时其规律性不一致，在快车道冲击系数呈现先增大后减小的趋势，在中车道呈现先增大后减小再增大的趋势，在慢车道呈现一直增大的趋势；随着车重的增加，冲击系数减小的幅度呈现逐渐减小的规律，轻车低速对桥梁的冲击效应更加显著；大多数工况下端部短吊杆的冲击系数均大于规范值，因此，在桥梁设计中应更加注重短吊杆的抗疲劳设计。

车桥耦合振动；轮迹横向分布；冲击系数；桥梁设计

三跨连续拱梁组合桥具有结构形式多样、刚度较大等优点，被越来越多工程所运用，其中也出现了造型独特的多拱肋钢拱桥，这类桥型具有复杂的结构使其动力特性比较特殊，近几年工程事故时有发生，其动力特性的研究显得尤为重要，一般用冲击系数作为研究动力特性的重要参数。张耀等[1]分析桥面不平顺等级，行车速度及车重对钢管混凝土系杆拱桥关键部位动力效应的影响。HUANG[2]研究桥面，拱肋及立柱的边界条件对钢管混凝土拱桥冲击系数的影响。杨建荣等[3]研究了钢管混凝土系杆拱桥各关键部位的位移，内力响应以及桥梁动力响应的频谱特征。孙全胜等[4]分析在不同速度下位移，速度及加速度等动力响应，对行车的舒适性进行研究。邵元等[5]从理论上分析桥面粗糙度和车速情况下，不同长度吊杆应力的变化规律，并通过车速分布图对应力冲击系数进行加权分析。朱劲松等[6]通过车桥耦合程序分析拱桥在车辆荷载作用下吊杆冲击系数的不均匀性问题。陈水生等[7]通过数值模拟分析车速及桥面平整度对主梁关键部位的冲击系数的影响，并通过实测值进行验证。韩艳等[8]基于车桥耦合程序，研究桥面粗糙度，行车速度，行车数量和行车间距等对桥梁跨中位置动力响应和冲击系数的影响。综上所述，国内外学者对拱桥这类桥型冲击系数的研究主要针对钢管混凝土拱桥，并仅对其中一根主梁或拱肋上关键部位冲击系数进行研究，但对于具有斜交角，并且边拱与竖直方向具有倾斜角度的拱梁组合桥，可能存在边主梁或边主拱的冲击系数大于中主梁或中拱肋的情况，其规律性还需要进一步研究。此外，目前程序计算冲击系数是按照移动荷载行驶在最不利加载位置得到最大动静挠度的比值，这与实际加载情况存在较大的差异。本文基于车桥耦合振动程序，得到三跨连续拱梁组合桥在移动车辆荷载作用下的冲击系数，并考虑轮迹横向分布的影响，按照多迹线加载方式来计算不同关键部位的冲击系数，这更符合车轮的实际加载情况。并对车道位置、桥面平整度、行驶速度和车重等多个影响因素进行分析，得到一些有意义的结论，对三跨连续拱梁组合桥的设计具有参考意义。

1 车桥耦合振动数值分析方法

1.1 桥梁模型

根据有限元法离散建立桥梁动力方程，用矩阵表示为：

桥梁结构的阻尼采用瑞利阻尼[9]。

式中：0和0的计算公式分别如下：

式中：1，2与1，2分别为桥梁的第一，二阶自振频率和第一，二阶模态阻尼。

1.2 车辆模型

车辆简化为三轴车的非线性力学模型，这种车辆模型的参数具有较好的代表性，如图1所示。wi为各车轮的质量；c1为车头质量，c2为车厢质量；ci为车体各仰俯转动惯量，ci为车体各侧滚转动惯量；sisi分别为各上部弹簧刚度系数和各上部弹簧阻尼系数；titi分别为各下部弹簧刚度系数和各下部弹簧阻尼系数；i为各轴距重心的距离。

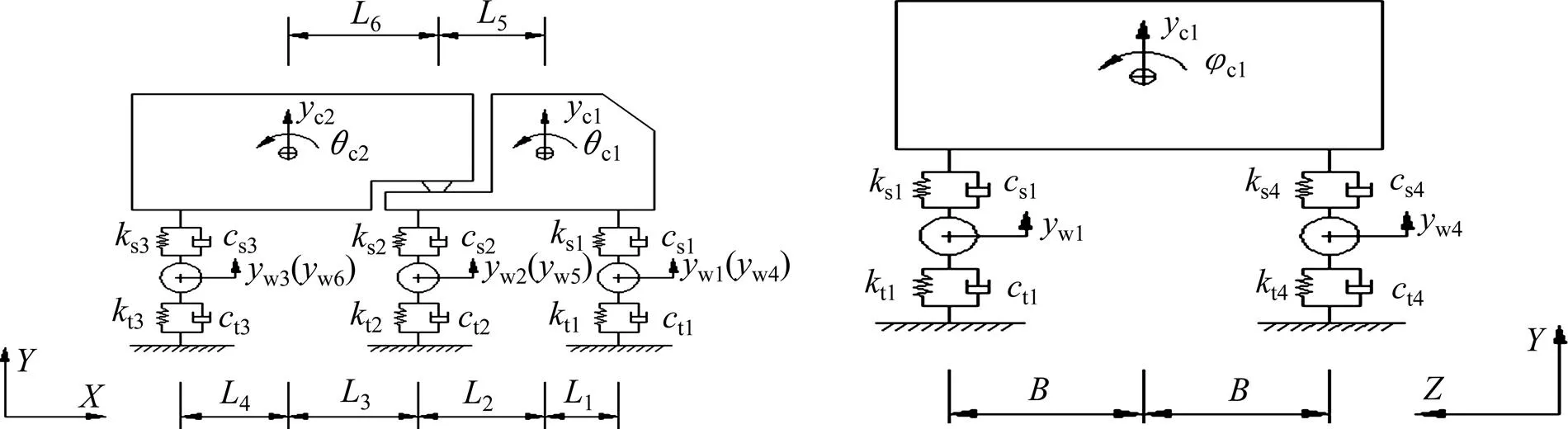
图1 三轴车模型

为便于计算，将车辆方程写成矩阵形式为：

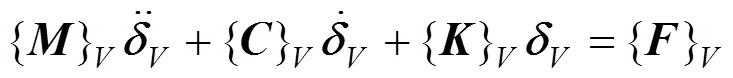
其中：=[w1w2w3w4w5w6c1c2c1c1c2]T为车辆的11个自由度向量，{}，{}和{}分别为车辆模型的质量矩阵，阻尼矩阵和刚度矩阵。{}为车辆模型所受的荷载向量[6]。

本文采用32.5 t车重[10]，通过修改车体质量c2获得其他重量的车辆参数。

1.3 桥面不平顺模型

桥面不平顺对桥梁动力响应的影响不可忽略，通常将桥面不平顺假定为均值为0的Gauss随机过程。Dodds等[11]提出的位移功率谱密度函数为：

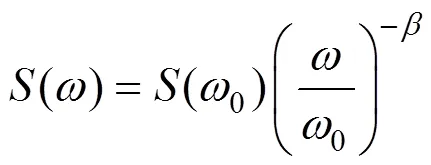
式中：为空间频率；w为间断频率桥面不平顺系数，取值为0.1 m−1，指数=1.94。

本文桥面不平顺样本通过三角级数叠加法[12]获得，其函数表达式如下：

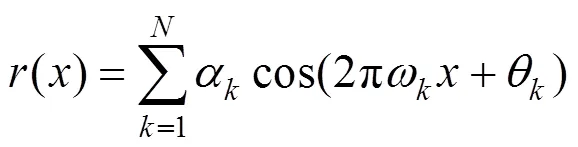
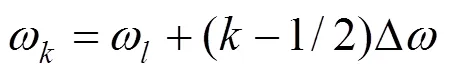
式中：为cos函数的幅值；为空间频率；为0到2π之间的的随机相位角；为随机产生的不平顺节点个数。桥面等级的划分是依据(0)的控制范围，将其划分为“很好”、“好”、“一般”、“差”和“很差”5个等级，对应的不平顺系数分别取(0.24，0.62，2.5，10，16)×10−6 m3/cycle。

1.4 车桥耦合方程的建立

假设车辆行驶在桥面时，车轮与桥面始终接触，车轮与桥面之间作用力用以下公式表达：

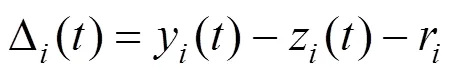
在车桥耦合系统中，把车辆和桥梁看作2个系统，是通过车轮和桥面接触处具有相同位移与相互作用力的协调条件将振动方程联系起来[6]。本文采用NewMark-b法对车桥耦合振动方程进行求解，基于Matlab开发的车桥耦合程序，对三跨连续拱梁组合桥的冲击系数进行分析。

2 算例分析

2.1 分析模型

以一座三跨连续拱梁组合桥为背景，其主桥部分采用新颖独特的全钢拱桥结构，桥孔布置为25+70+25 m，桥长120 m，全宽43 m，桥梁横向为整体设计，桥梁平面按斜交85°设计。两侧25 m边跨为钢结构梁桥，中跨为70 m下承式钢结构拱桥，中跨主受力结构由2道边拱和1道中拱组成。边拱拱平面与竖直方向夹角12°，向内倾斜。桥梁总体布置如图2所示。

(a) 横截面图；(b) 立面图

采用ANSYS建立三跨连续拱梁组合桥的有限元模型。桥梁结构主要构件钢材均采用钢材Q420qD。桥面系纵横梁、拱肋、拱间联系和风撑均采用梁单元BEAM188来模拟，桥面板采用壳单元SHELL63来模拟，吊杆采用只受拉的杆单元Link10来模拟，纵桥向吊杆编号为1号至7号，二期恒载采用质量单元MASS21来模拟。全桥各类单元共16 038个，节点共8 234个。

2.2 分析工况

分析不同桥面平顺度、行车速度、车辆横向位置、车道和车重等影响因素下车桥耦合系统的动力响应及桥梁各关键部位的冲击系数。分析工况见表1，选取2号和3号主梁之间的车道进行分析，左偏是表示靠近2号中主梁，右偏是表示靠近3号边主梁，该桥共双向6车道，快车道是表示靠近2号中主梁的车道，慢车道是表示靠近3号边主梁的车道。

表1 分析工况

2.3 分析结果

2.3.1 轮迹横向分布对冲击系数的影响

在桥梁设计中，冲击系数需按照最不利加载位置下的动力响应来计算[13]，这与实际车轮的加载有所偏差，没有考虑车辆行驶在车道宽度范围是以一定的概率横向分布形式。将车辆沿着我国规范轮迹分布模型图中的各轮迹带中心线进行加载[14]，计算得到各关键部位的冲击系数，选取2号主梁及相应的主拱和吊杆为对象进行分析。

图3 轮迹横向分布

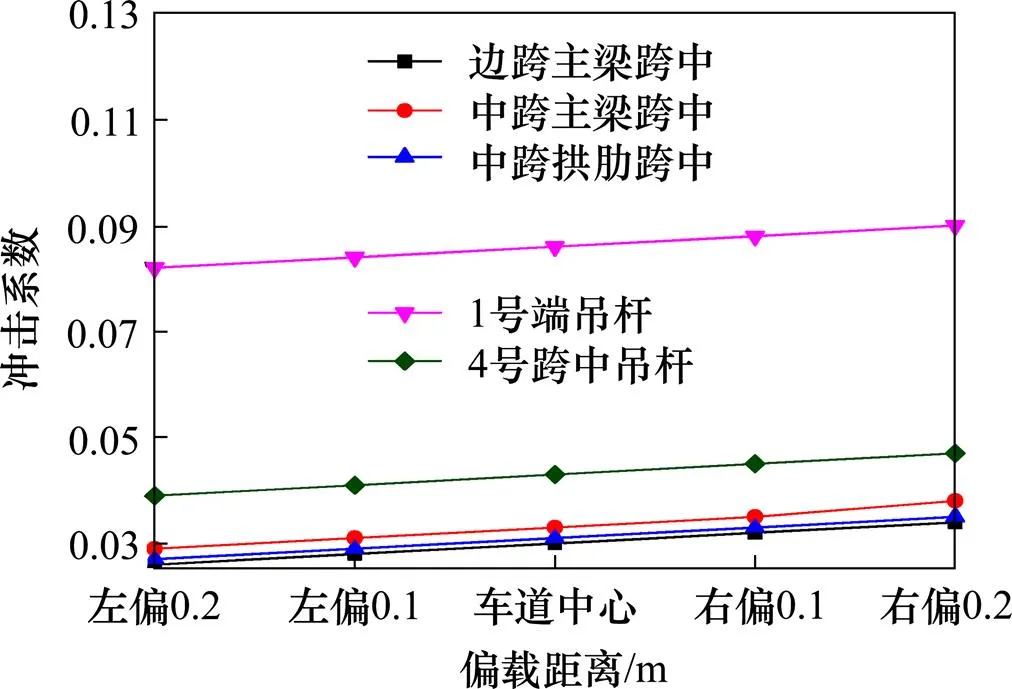
图4 不同偏载距离冲击系数对比曲线

图3为轮迹横向分布频率模型，图4为桥梁各个关键部位冲击系数随偏载距离变化曲线。考虑横向分布频率后，计算得到边跨主梁跨中、中跨主梁跨中、中跨拱肋跨中、1号和4号吊杆的冲击系数分别为0.030，0.032，0.031，0.086和0.043，这与车辆行驶在车道中心时计算得到的冲击系数相近。因此，以后用有限元法计算冲击系数时可以直接采用车辆行驶在车道中心位置。右偏车道中心线0.2 m，对冲击系数的贡献最大，随着轮迹位置继续向横向偏移，冲击系数线性减少。由图4可以看出，吊杆比桥梁其他关键部位的冲击系数高，并且1号端吊杆比4号跨中吊杆的冲击系数大1.96倍，运营期间应加大对端吊杆的养护力度。

2.3.2 不同车道对冲击系数的影响

为了研究车辆在不同车道行驶时对拱桥冲击系数的影响，取快车道、中车道和慢车道3种车道进行分析，行车速度为60 km/h，车重采用标准车32.5 t。

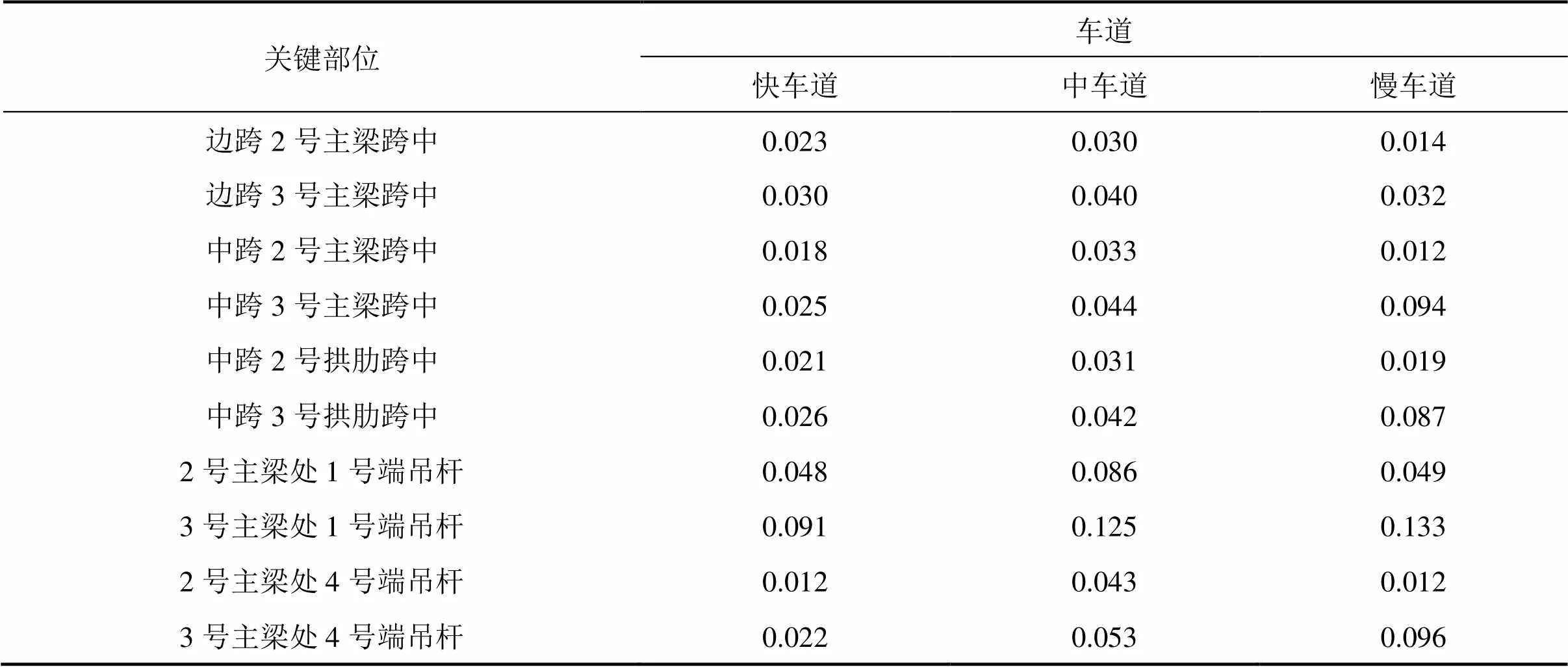
表2 不同车道下桥梁关键部位的冲击系数

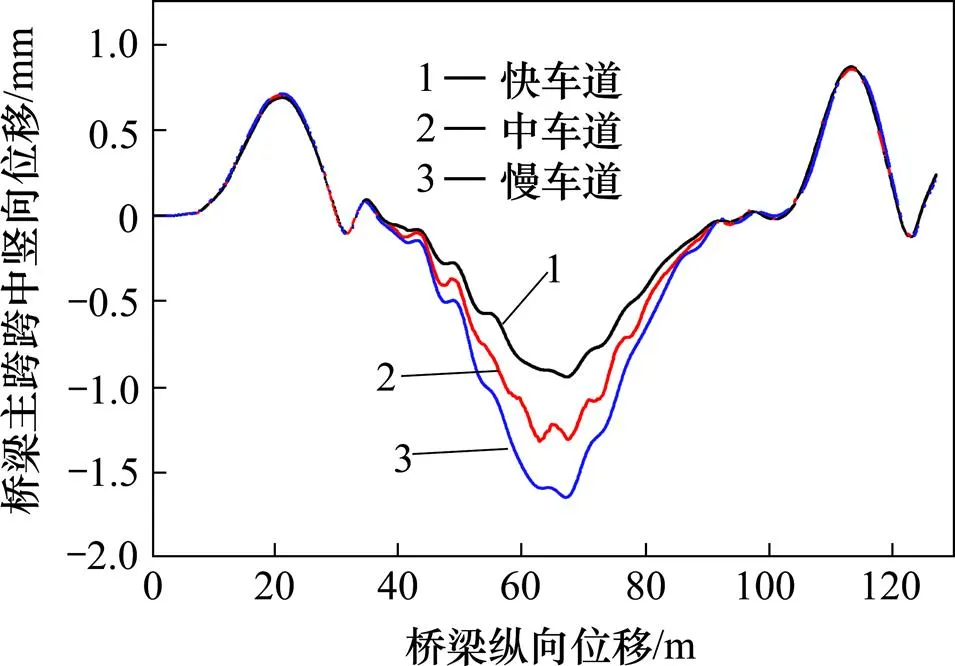
图5 中跨2号主梁跨中位移响应曲线

表2为不同车道下桥梁结构各个关键部位的冲击系数。图5为中跨2号主梁跨中的振动响应图。从表2可得，不论车辆行驶在快车道、中车道还是慢车道，2号主梁、中拱肋及直吊杆的冲击系数总是小于相应3号主梁、边拱肋及斜吊杆的冲击系数。对于2号主梁、中拱肋及直吊杆，随着车辆从快车道向慢车道行驶冲击系数先增大后减小，但从图5可以看出，主梁的动位移在逐渐增大，因此，动位移的大小并不能代表冲击系数的大小，评价桥梁动力性能用冲击系数更为准确。对于3号主梁、边拱肋及斜吊杆，除了边跨主梁跨中，冲击系数随着车辆从快车道向慢车道行驶先增大后减小，其他关键部位的冲击系数，都在逐渐增大，且中跨3号主梁跨中、中跨3号拱肋跨中、3号主梁处1号端吊杆和4号吊杆的冲击系数在快车道工况较慢车道工况分别增大3.84，3.34，1.46和4.36倍。

2.3.3 不同平整度对冲击系数的影响

为了研究桥面平整度对拱桥冲击系数的影响，分别取9种不平顺系数0.24×10−6，0.62×10−6，2.5×10−6，4×10−6，7×10−6，10×10−6，13×10−6，16×10−6，19×10−6 m3/cycle进行计算分析，行车速度为60 km/h，车重采用标准车32.5 t。选取2号主梁及相应的主拱和吊杆为对象进行分析。

图6为桥梁构件各个关键部位冲击系数随不平顺系数变化曲线。图7为中跨主梁跨中的振动响应图。由结果可得，边跨主梁跨中、中跨拱肋跨中的冲击系数普遍比中跨主梁跨中的小，吊杆的冲击系数普遍比中跨主梁跨中的大，可见，对于三跨连续拱梁组合桥来说，跨径越长，冲击系数越大。在桥面平整度为“一般”时，1号端吊杆和4号跨中吊杆的冲击系数几乎相等，桥面平整度为“很好”和“好”时，1号端吊杆的冲击系数高于4号跨中吊杆，桥面平整度为“差”和“很差”时，结果相反，说明路面平整度越差，对长吊杆冲击系数的影响要大于短吊杆。桥面越不平整，各个关键部位的动挠度均增大，冲击系数也随之增加，且有相似的变化规律，随着桥面退化程度的增加呈非线性增长，至E级桥面等级时，边跨主梁跨中、中跨主梁跨中、中跨拱肋跨中、1号端吊杆、4号跨中吊杆的冲击系数分别是A级桥面的6.97，10.848，10.258，5.326和11.535倍，加快了桥梁结构的疲劳。参考JTG D60-2015公路桥涵设计通用规范[15]规定的方法，此桥的一阶自振频率为1.503 Hz，计算得到桥梁冲击系数为0.056。以中跨主梁跨中部位为例，随着桥面不平顺系数的增加，冲击系数分别为0.033，0.069，0.133，0.171，0.231，0.279，0.321，0.358和0.391，除桥面平整度为“很好”情况下基本满足我国规范取值，其他等级情况下均大于我国规范，评估现役桥梁时，冲击系数的计算值偏于不安全，根据冲击系数影响曲线，得到各个关键部位冲击系数与振动系数的关系均满足幂函数，可供以后规范的冲击系数计算公式修正参考。因此，在桥梁运营期间，要注意及时对桥梁桥面进行整修，这对保证结构安全和减少汽车对桥梁的冲击作用是很有必要的。

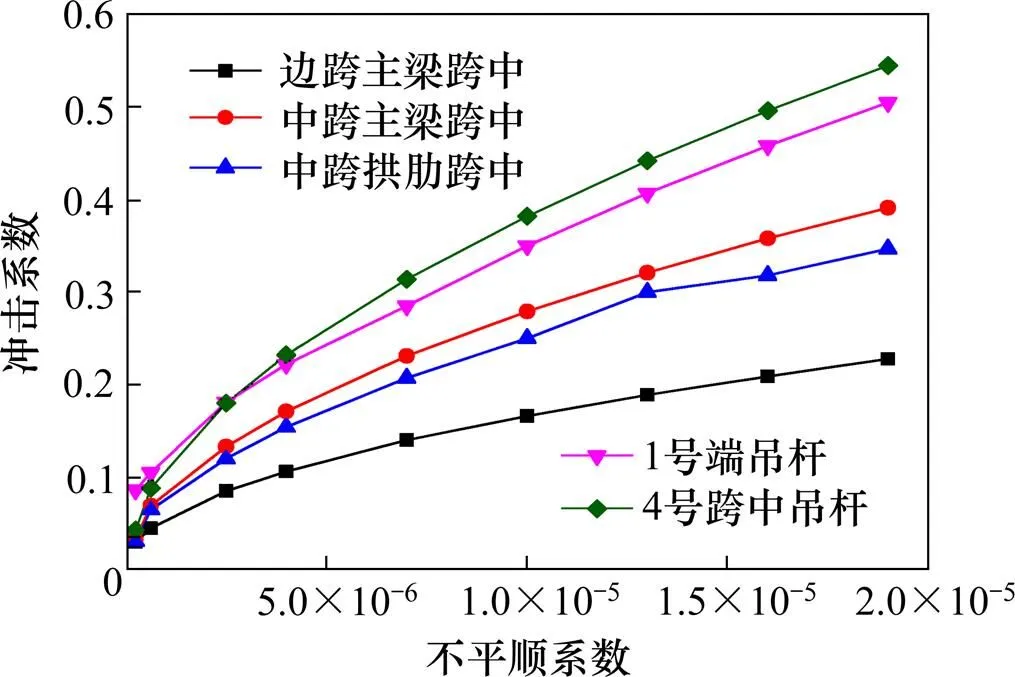
图6 不平顺系数对冲击系数的影响曲线

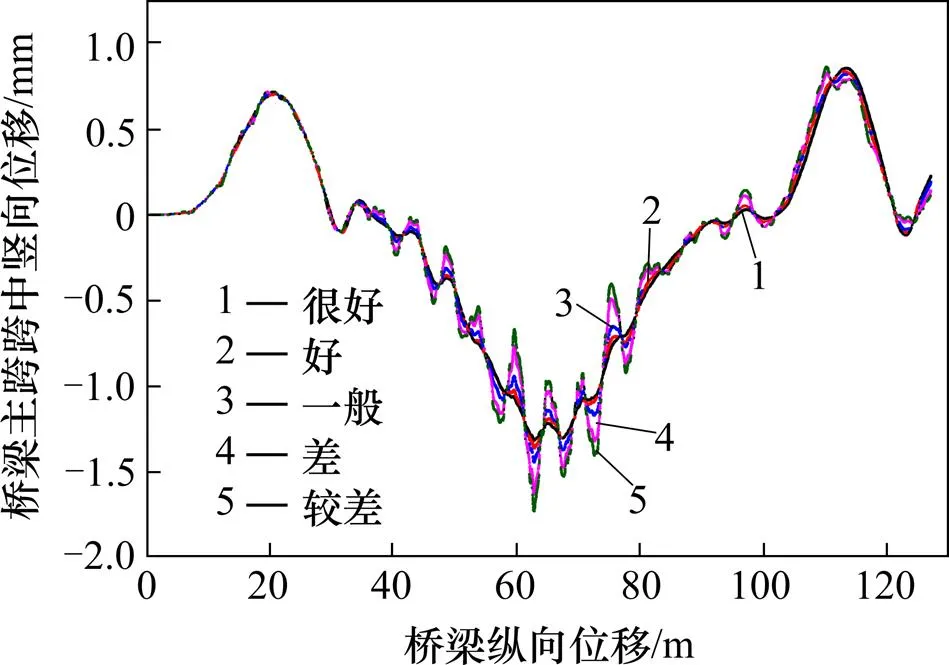
图7 中跨主梁跨中竖向位移响应曲线

2.3.4 不同车道的车速差对冲击系数的影响

为了研究不同车道的车速差对拱桥冲击系数的影响，分别在快车道、中车道和慢车道取20，40，60，80和100 km/h行车速度进行分析，桥面平整度取“很好”情况，车重采用标准车32.5 t。限于篇幅，关键部位选取2号中跨主梁跨中为对象进行分析。

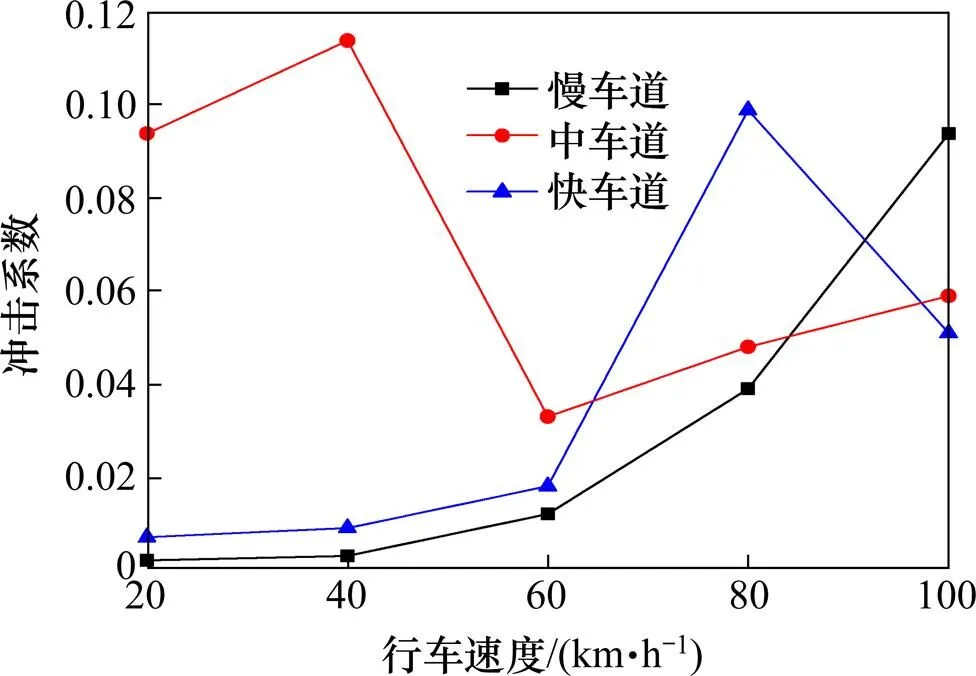
图8 不同车道的不同车速下中跨主梁跨中冲击系数对比曲线

图8为桥梁中跨主梁跨中部位在不同车道的冲击系数随车速变化曲线。车辆在快车道行驶时，在20~80 km/h时先增大，80~100 km/h再减小，在车速80 km/h时出现了极大值。在中车道行驶时，车速在20~40 km/h时先增大，40~60 km/h后减小，60~100 km/h再增大，在车速40 km/h时出现了极大值，60 km/h时出现了极小值。在慢车道行驶时，基本呈现一直增大的趋势。冲击系数出现极大值，从能量的角度，这是由于车速低时车桥相互作用的能量小但作用时间长，车速高时车桥相互作用的能量大但作用时间短，到达某一速度时两者作用效应达到最不利状态，此时冲击系数最大。从振动的角度，以车辆行驶在中车道的中跨主梁跨中这一部位为例，由加速度时程响应经傅里叶变换获得的频谱图可得，当车速在40 km/h时，此时桥梁结构基频为2.179 Hz，车速在20，60，80和100 km/h时桥梁结构的基频分别为2.14，1.36，1.53和1.72 Hz，而桥梁的一阶竖弯固有振动频率为2.17 Hz，车速在40 km/h时与桥梁的一阶竖弯固有振动频率比较接近，振动效应增大，此时冲击系数最大。在常见的行车速度范围内，三跨连续拱梁组合桥的边跨冲击系数小于中跨的，长吊杆的冲击系数小于端吊杆的，当行车速度位于60~80 km/h区间时，采用公路桥涵设计通用规范所取的冲击系数基本适用。

2.3.5 不同车重的车速差对冲击系数的影响

为了研究不同车重的车速差对拱桥冲击系数的影响，分别采用10，32.5，40和55 t车重以20，40，60，80和100 km/h行车速度进行分析，桥面平整度取“很好”情况。限于篇幅，关键部位选取2号中跨主梁跨中部位为对象进行分析。

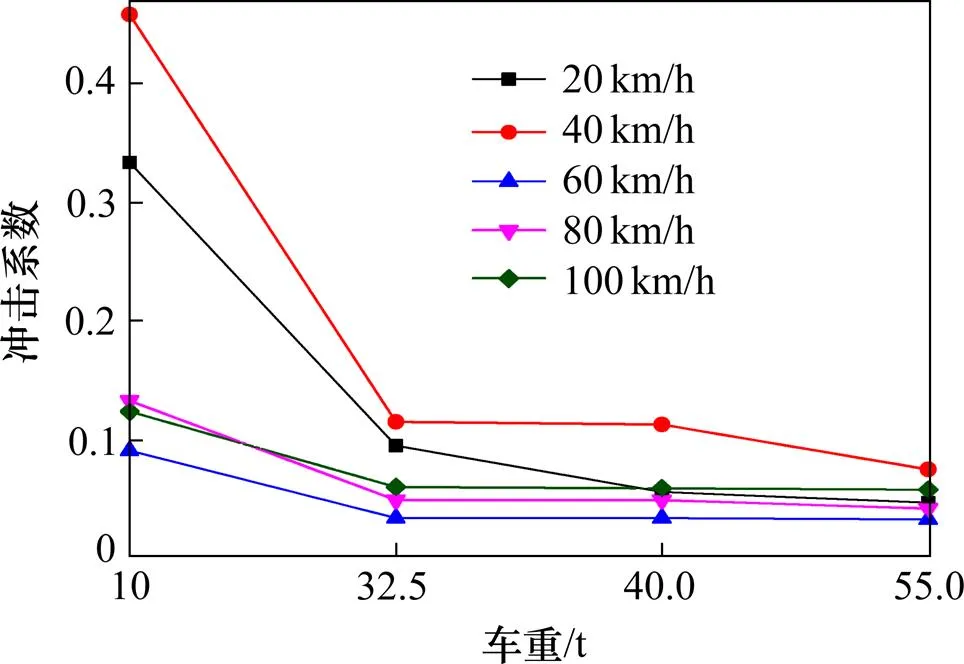
图9 不同车重的不同车速下中跨主梁跨中冲击系数对比曲线

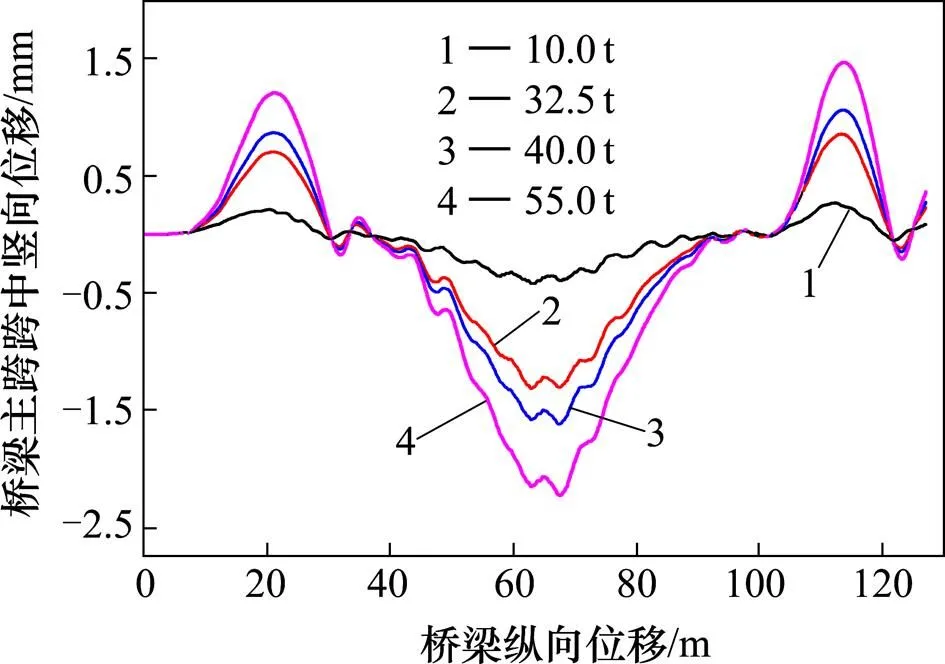
图10 中跨主梁跨中竖向位移响应曲线

图9~10分别为不同速度下冲击系数随车重变化的曲线和竖向位移响应。中车道行驶时，随车速的增加，不同车重的车辆也满足车速在20~40 km/h时先增大，40~60 km/h后减小，60~100 km/h再增大，在40 km/h时出现了极大值的规律。随着车重的增大，桥梁的冲击系数均呈现减小的趋势，10 t相对于55 t车辆在中跨主梁跨中处冲击系数降幅分别为0.287，0.384，0.058，0.091和0.066。冲击系数减小的趋势是由于随着车重的增加，结构的刚性增强，振动效应逐渐减轻，车辆行驶更加稳定，因此冲击系数会逐渐减小。由此可见，轻车低速对桥梁的冲击效应更加显著。从图10来看，随车重增加，中跨主梁跨中的竖向位移显著增大。由图9可知，冲击系数在车重10~32.5 t之间降幅最大，在此车重范围内，冲击系数受车重影响较大。虽然重车的冲击系数小，但其动静荷载效应远大于轻车，因此有必要控制超载情况。

3 结论

1) 按照我国《公路钢结构桥梁设计规范》的轮迹分布模型图中的各轮迹带中心线分别对桥梁进行加载，计算得到冲击系数与车辆在车道中心线加载的结果相近。因此，以后按有限元法计算冲击系数可以直接在车道中心线加载；

2) 中跨3号主梁跨中、中跨3号拱肋跨中、3号主梁处1号端吊杆、3号主梁处4号吊杆的冲击系数在快车道工况较慢车道工况分别增大3.84，3.34，1.46和4.36倍。车辆行驶在任意车道时，3号边主梁、边拱肋及斜吊杆的冲击系数都大于相应2号中主梁、中拱肋及直吊杆。

3) 在桥面平整度为“很好”时，各关键部位的冲击系数跟规范值接近，但随着桥面退化程度的增加，各关键部位的冲击系数呈非线性增长，各关键部位的冲击系数与振动系数均满足幂函数关系，加快了桥梁结构的疲劳，因此，有必要定期对桥面铺装层进行养护。

4) 随着车速的增加，冲击系数在不同车道的规律性并不一致，车辆在慢车道行驶时，基本呈现一直增大的趋势，在中车道上冲击系数并未呈现一直增加的趋势，而是先增大后减小再增大的趋势，在快车道行驶时，冲击系数先增大，再减小，建议控制车速位于60~80 km/h区间有利于减少车辆对桥梁的冲击作用。

5) 随着车重的增加，各关键部位冲击系数减小幅度逐渐减小，轻车低速对冲击系数影响较大。

6) 根据本文分析，大多数工况端部短吊杆的冲击系数超过规范的规定值，这与实际工程中短吊杆常发生疲劳断裂的事故相吻合。因此，在桥梁设计中应更加注重短吊杆的抗疲劳设计。

[1] 张耀, 孙增寿. 基于车桥耦合振动的钢管混凝土系杆拱桥动力响应分析[J]. 铁道科学与工程学报, 2016, 13(1): 103−110. ZHANG Yao, SUN Zengshou. Analysis of concrete– filled steel tubular tied–arch bridge under travelling vehicles[J]. Journal of Railway Science and Engineering, 2016, 13(1): 103−110.

[2] HUANG Dongzhou. Vehicle–induced vibration of steel deck arch bridge and analytical methodology[J].Journal of Bridge Engineering, 2012, 17(2): 241−248.

[3] 杨建荣, 李建中, 申俊昕. 钢管混凝土系杆拱桥车桥耦合振动分析[J]. 北京工业大学学报, 2012, 38(6): 847− 853. YANG Jianrong, LI Jianzhong, SHEN Junxin. Numerical investigation of concrete-filled steel tubular tied-arch bridge under travelling vehicles[J]. Journal of Beijing University of Technology, 2012, 38(6): 847−853.

[4] 孙全胜, 张立东, 张盛然. 车辆速度对大跨斜拉桥行车舒适性的影响分析[J]. 中外公路, 2017, 37(1): 114−117. SUN Quansheng, ZHANG Lidong, ZHANG Shengran. Impact of vehicle speed on driving comfort of large span cable-stayed bridge[J]. Journal of China & Foreign Highway, 2017, 37(1): 114−117.

[5] 邵元, 孙宗光, 陈一飞, 等. 车辆荷载对中承式拱桥吊杆体系的冲击效应分析[J]. 公路交通科技, 2016, 33(1): 82−88. SHAO Yuan, SUN Zongguang, CHEN Yifei, et al. Analysis of impact effect of vehicle load on hanger system of half-though arch bridge[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 82−88.

[6] 朱劲松, 邑强. 中下承式拱桥吊杆应力冲击系数不均匀性研究[J]. 振动与冲击, 2012, 31(13): 5−10. ZHU Jinsong, YI Qiang. Non-uniformity of stress impact factor of suspenders on half-through or through arch bridges[J]. Journal of Vibration and Shock, 2012, 31(13): 5−10.

[7] 陈水生, 孙百传. 基于车桥耦合钢管混凝土拱桥车辆的冲击系数[J]. 南昌大学学报(工科版), 2017, 39(1): 32−36. CHEN Shuisheng, SUN Baichuan. The impact coefficient of the concrete filled steel tube arch bridge based on the vehicle-bridge coupling vibration[J]. Journal of Nanchang University (Engineering & Technology), 2017, 39(1): 32−36.

[8] 韩艳, 李浩, 薛繁荣. 基于车桥耦合的钢管混凝土拱桥车桥冲击系数研究[J]. 铁道科学与工程学报, 2016, 13(3): 493−499. HAN Yan, LI Hao, XUE Fanrong. Research on the impact coefficientof the concrete filled steel tube arch bridge based on the vehicle−bridge coupled vibration[J]. Journal of Railway Science and Engineering, 2016, 13(3): 493−499.

[9] Leitao P N, Silva J G S, Vellasco P C G D, et al. Composite (steel-concrete) highway bridge fatigue assessment[J]. Journal of Constructional Steel Research, 2011, 67(1): 14−24.

[10] ZHANG W, CAI C S. Fatigue reliability assessment for existing bridges considering vehicle speed and road surface conditions[J]. Journal of Bridge Engineering, 2012, 17(3): 443−453.

[11] Dodds C J, Robson J D. The description of mad surface roughness[J]. Journal of Sound and Vibration, 1973, 31(2): 175−183.

[12] Au F T K, Cheng Y S, Cheung Y K. Effects of random road surface roughness and long-term deflection of prestressed concrete girder and cable-stayed bridges on impact due to moving vehicles[J]. Computers & Structures, 2001, 79(8): 853−872.

[13] 邓露, 王维. 公路桥梁动力冲击系数研究进展[J]. 动力学与控制学报, 2016, 14(4): 289−300. DENG Lu, WANG Wei. Research progress on dynamic impact coefficient of highway bridges[J]. Journal of Dynamics and Control, 2016,14(4): 289−300.

[14] JTG D64—2015, 公路钢结构桥梁设计规范[S]. JTG D64—2015, Specifications for design of highway steel bridge[S].

[15] JTG D60—2015, 公路桥涵设计通用规范[S]. JTG D60—2015, General specifications for design of highway bridges and culverts[S].

Research on the impact factor of the three-span continuous beam-arch combined bridge based on the vehicle-bridge coupled vibration

ZHU Jinsong1, 2, XU Yufeng1

(1. School of Civil Engineering, Tianjin University, Tianjin 300072, China; 2. Key Laboratory of Coast Civil Structure Safety (Tianjin University), Ministry of Education, Tianjin 300072, China)

In order to analyze and calculate the impact factor of key parts of bridge structure, the three-span continuous beam-arch combined bridge was taken as an example to investigate the impact factors. Three-dimensional element model and a vehicle spatial model with 11 degree of freedom were established by using the MATALAB software and ANSYS software, respectively. The vibration responses of the key parts of bridge structure could be obtain by using the vehicle load with the vehicle-bridge coupling method. The results of the study indicate: regardless of which lane the vehicle is driving, the side main girder, side arch ribs, and slanting suspenders are larger than the impact factor of the corresponding middle girder, middle arch rib, and straight suspenders; as the level of roughness increases, the impact factor of key parts shows nonlinear increase, the relationship between the impact coefficient and the vibration coefficient satisfies the power function; the regularity of vehicles varies in different lanes, the impact coefficient increases first and then decreases in the fast lane, it tends to increase firstly, then decreases and then increases in the middle lane, the trend has been increasing in the slow lane; the decreasing rate of the impact factor shows a decreasing trend with increases in vehicle weight, the impact effect of light vehicle in low speed on bridge is more significant; the impact factor of the suspender at the lower end of most working conditions is greater than the standard value, so we should pay more attention to anti-fatigue design short boom after the bridge design.

vehicle-bridge coupling vibration；wheel trace transverse distribution；impact factor；bridge design

10.19713/j.cnki.43−1423/u.2019.04.017

U441.3

A

1672 − 7029(2019)04 − 0959 − 09

2018−05−30

国家自然科学基金面上资助项目(51578370)；天津市科技支撑计划重点资助项目(16YFZCSF00460)；天津市自然科学基金资助项目(京津冀合作专项项目)(16JCZDJC40300)

朱劲松(1975−)，男，安徽池州人，教授，博士，从事桥梁结构全寿命设计、施工控制、健康监测的研究与教学工作；E−mail：jszhu@tju.edu.cn

(编辑 阳丽霞)