状态观测器参数对磁浮车辆悬浮稳定性影响的仿真研究

梁潇，马卫华，肖溪玥，陈晓昊



状态观测器参数对磁浮车辆悬浮稳定性影响的仿真研究

梁潇1,3，马卫华2，肖溪玥3，陈晓昊2

(1. 长沙理工大学 土木工程学院，湖南 长沙 410014； 2. 西南交通大学 牵引动力国家重点实验室，四川 成都 610031； 3. 湖南磁浮技术研究中心有限公司，湖南 长沙 410000)

为研究磁浮车辆悬浮控制器的状态观测器参数对悬浮稳定性的影响，解决磁浮车辆悬浮不稳的问题，建立单电磁铁与柔性轨道梁的耦合模型。通过对悬浮系统传递函数的研究，得到速度激励信号频率与悬浮系统对轨道梁的功率输出的关系曲线，并得到状态观测器参数对系统性能的影响规律。由此得出结论，通过绘制“悬浮系统对轨道梁的振动能量输出功率”与“轨道梁主频率”间的关系曲线，即可得到不考虑轨道梁阻尼时，悬浮系统可适应轨道的临界参数。

悬浮系统；传递函数；输出功率；临界频率

随着国民经济的发展，中国城市交通越来越拥堵[1]。发展公共交通是改善城市交通状况的有效途径。与传统的轨道交通系统相比，电磁悬浮模式磁浮列车具有噪音低、速度快、爬陡坡能力强等优点，是近几年来备受关注的一种新型城市交通方式[2]，许多国家都对其开展了研究，并取得了很大的进步。磁浮列车的迅速发展和巨大优势，为其商业应用提供了广阔的前景。但也应该指出，目前还存在一些问题对磁浮列车的工程运用造成阻碍，例如车桥耦合系统的自激振动就是一个亟待解决的问 题[3]。由于轨道的结构特点，轨道梁的柔性显著影响磁浮车辆运行的稳定性与平稳性，特别是在静止或低速运动时，容易产生耦合振动造成悬浮系统的不稳定[4−5]。人们普遍接受的结论是，高架轨道梁的柔性，是造成这种现象的主要原因[6−7]。针对磁浮列车与轨道梁的耦合振动问题，梁鑫[8]系统地阐述磁轨关系特点与控制系统参数对磁浮车辆振动的影响；赵春发等[9−10]将车辆简化为5刚体10自由度的质量块模型，将电磁力等效为线性弹簧−阻尼力，建立高速磁浮车辆−轨道梁耦合振动模型；邹东升等[11]针对车轨耦合悬浮系统中的振动现象，利用双环PID算法控制，研究其产生的根源，总结出悬浮车轨耦合系统会出现同宿分岔、Hopf分岔、二次Hopf分岔和混沌，认为这是悬浮系统振动的根源；王洪坡等[12−13]分别研究控制系统时滞对悬浮系统稳定性的影响，分析在位置时滞和轨道扰动共同作用下，悬浮系统在平衡点的1:3亚谐共振响应，并指出时滞参数不但可以抑制亚谐响应，还能控制混沌的产生。张玲玲[14]分别应用中心流形和正规型理论、Pseudo-Oscillator分析的摄动方法计算Hopf分岔引起的周期解，并用数值仿真验证了其有效性。由于物理意义明确、瞬态响应好、鲁棒性强且易于工程实现，PD控制器仍然是EMS系统中最常用的控制器之一[15]。EMS系统使用的PD控制器需要对悬浮间隙、振动速度与振动加速度3个状态进行反馈，而实际工程中的悬浮传感器只能检测悬浮间隙和电磁铁振动加速度信号，振动速度信号需要经过状态观测器计算得到，本文基于这一点对状态观测器对悬浮稳定性的影响进行研究。

1 系统模型

由于耦合振动现象的复杂性，为研究磁浮车辆与轨道梁耦合振动的情况，在建模时需要对模型进行简化处理以得出有益的结论，因此以一个柔性轨道梁与一个单一的悬浮电磁铁作为研究对象。

1.1 轨道梁模型

磁浮线路多采用高架方式，高架磁浮轨道由水泥支墩、单跨水泥梁、轨枕和钢轨等部分组成，目前大部分研究都将高架轨道简化为简支Euler- Bernoulli梁，其方程如下：

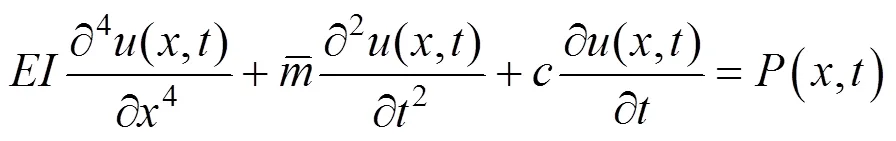
图1 简支梁-电磁铁耦合模型

Fig. 1 Simply supported beam-electromagnet coupling model

根据模态叠加理论，梁的挠度可以表示为振型函数与广义坐标的积：

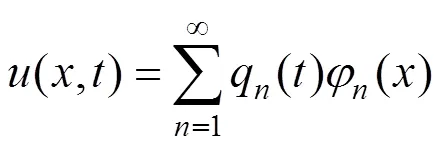
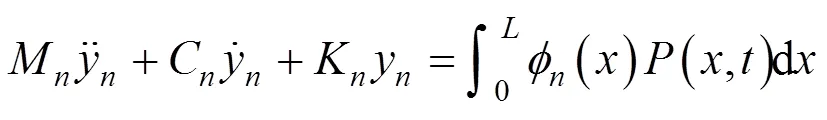
由于耦合振动现象发生时，轨道梁的高阶主频成分很少，所以只考虑轨道梁的一阶振动是合理的。轨道梁方程化简为：

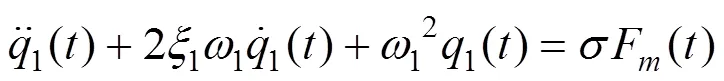
1.2 悬浮系统模型

根据EMS型常导磁浮车辆悬浮原理，电磁铁位于固定轨道下方，可以自由移动，电磁铁输入控制电压()，为电路中总电阻；0为真空磁导率；为线圈匝数；()为控制电路中的时变电流；为磁极面积；()为悬浮间隙，悬浮力(,)为电流与悬浮间隙的函数。

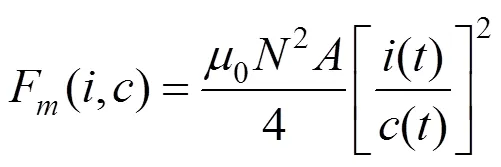
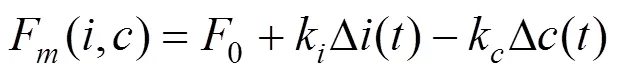
时变电流由控制电压驱动，控制电压同时驱动2个电磁铁。根据基尔霍夫定律，时变电流与控制电压的关系可以写成：

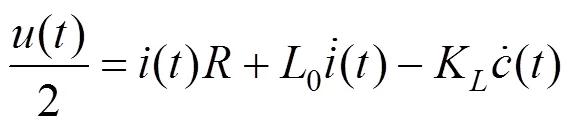
电磁铁的动力学方程为：

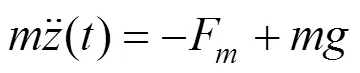
其中：()为电磁铁的垂向位移；为单个电磁铁运载质量；为重力加速度。

根据式(5)、(8)可得电磁铁静态电流：

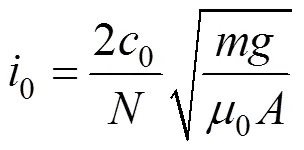
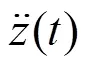
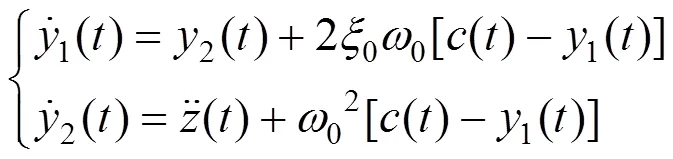
其中：2(t)即为观测器得到的速度信号，可得目标悬浮电流为：

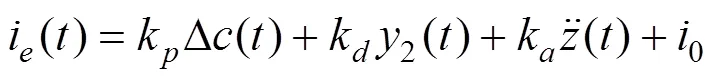
其中：k，k和k为3个状态的反馈系数。

为加快电流跟踪速度，使用电流环反馈：

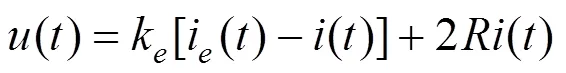
其中：k为电流反馈系数。

式(5)~(12)确定了悬浮系统的运动。

2 耦合振动机理

不考虑轨道梁柔性的情况下，悬浮系统往往可以得到稳定的结果，但是在考虑轨道梁的柔性时，系统有时会发生自激振动而失稳。由于轨道梁只在有能量输入的情况下振动才会加剧[7]，下面考虑电磁铁对轨道梁的能量输入。

2.1 电磁铁对轨道梁的能量输入与观测器系数的关系

根据式(5)~(12)，可得悬浮系统的线性化频域方程：

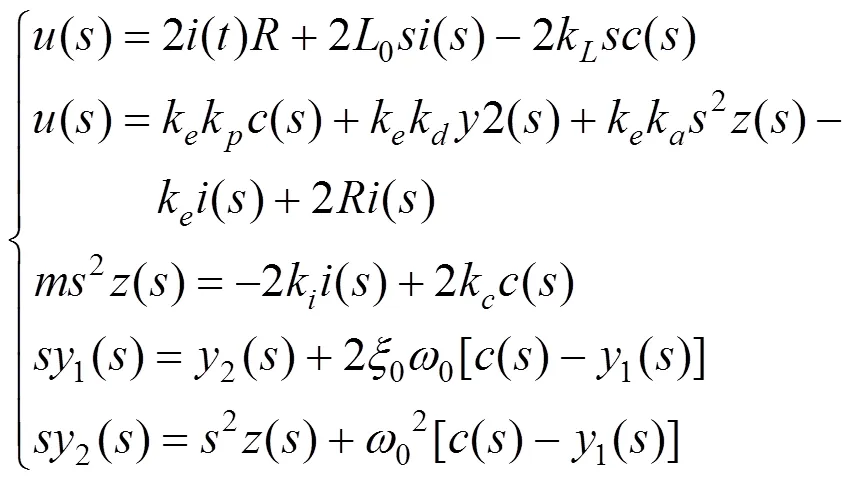
经过整理，可以得到以轨道梁振动速度为输入，电磁铁对轨道梁的作用力为输出的悬浮系统传递函数：

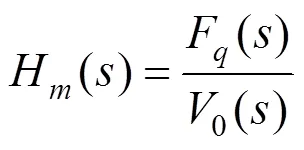
假设时刻，梁的振动圆频率为w，振动幅值为0.1 m/s，即：

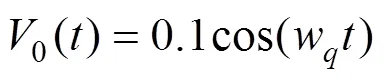
根据式(14)，电磁铁对轨道梁的作用力为：

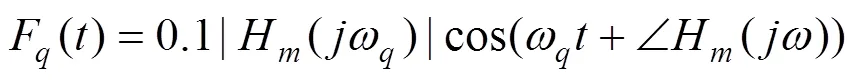
根据式(15)和(16)，电磁铁对轨道梁的平均输出功率为[16]：

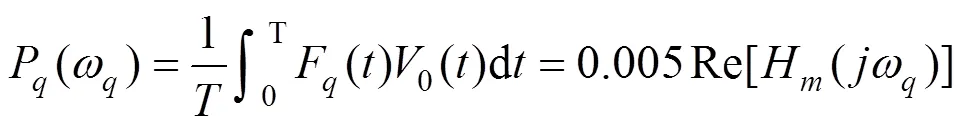
为研究观测器参数0和0对悬浮稳定性的影响，利用数值方法，可以得到电磁铁对轨道梁的输出功率P与梁的振动圆频率的关系。令=3 125 kg，0=8 mm，=360匝，=0.55 Ω，=0.018 4 m2，k=6 500，k=40，k=0.5，k=40。固定0=2，研究0对电磁铁对轨道梁的输出功率的影响，见图2。

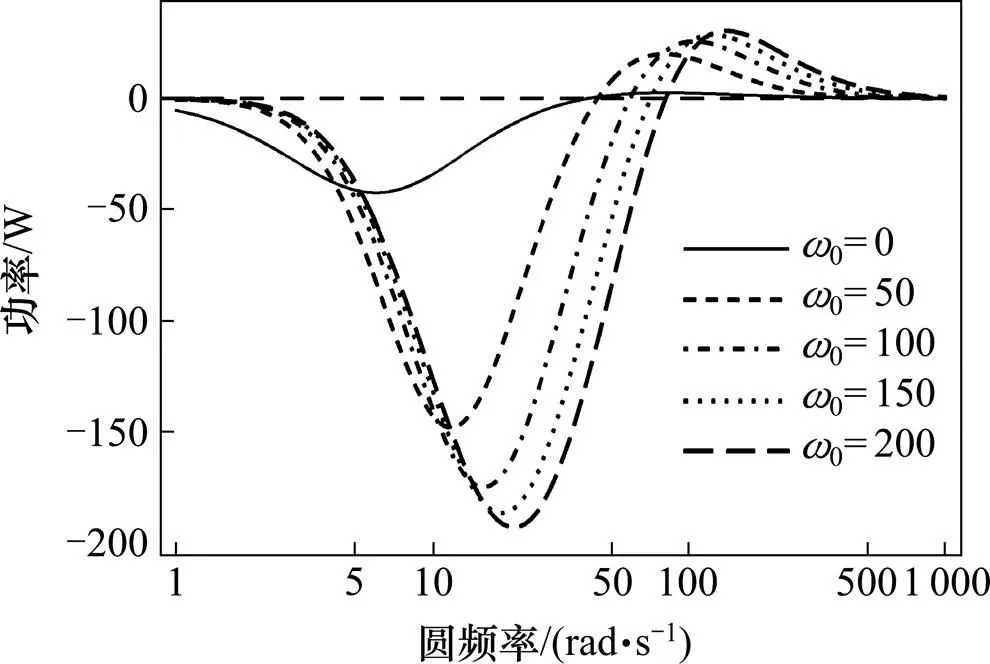
图2 ω0对电磁铁对轨道梁的输出功率的影响

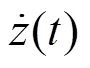
固定0=140，研究0对电磁铁对轨道梁的输出功率的影响，见图3。

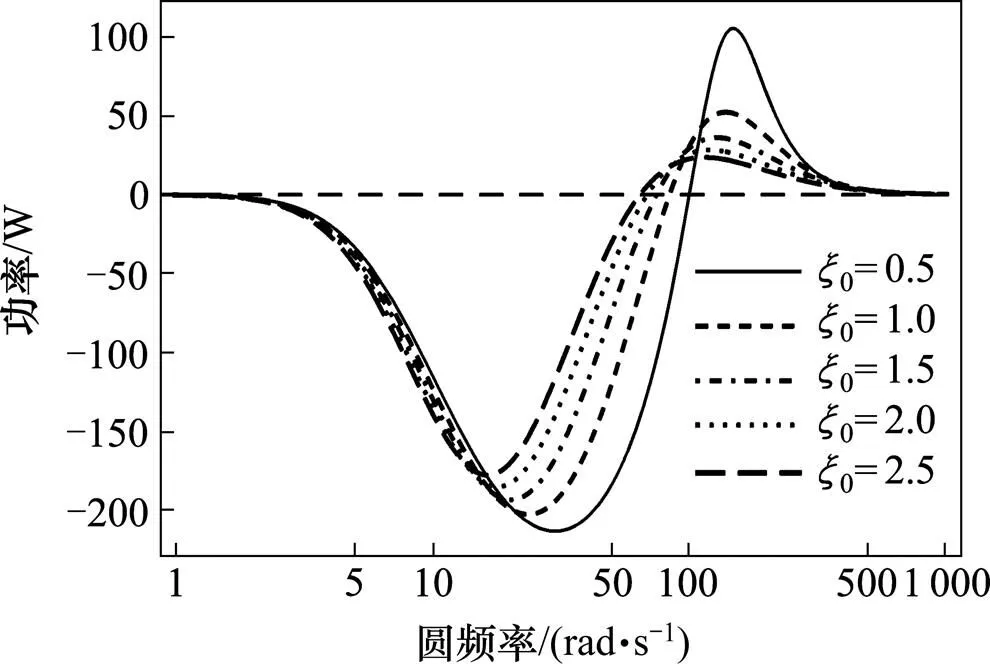
图3 ξ0对电磁铁对轨道梁的输出功率的影响

由图3可知，随着0的增大，临界频率有所减小，系统对高频激振的功率输出也随之减小，对中频振动的衰减能力也随之减小。但是，随着0的增大，系统引入的间隙传感器信号()的微分成分会有所减小，系统噪声会有所减小。

由上述分析可知，在不考虑间隙传感器的微分噪声的情况下，增大0减小0可以显著改善系统性能，但过大的0过小0又会引入不能忽视的系统噪声，实际工程中，观测器参数应在不引入过大噪声的前提下选取较大的0与较小的0。

2.2 悬浮系统可适应的轨道与观测器参数的关系

将式(4)描述的轨道梁方程与式(5)~(12)描述的悬浮系统方程联立并整理得到耦合系统的状态空间方程：

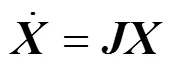
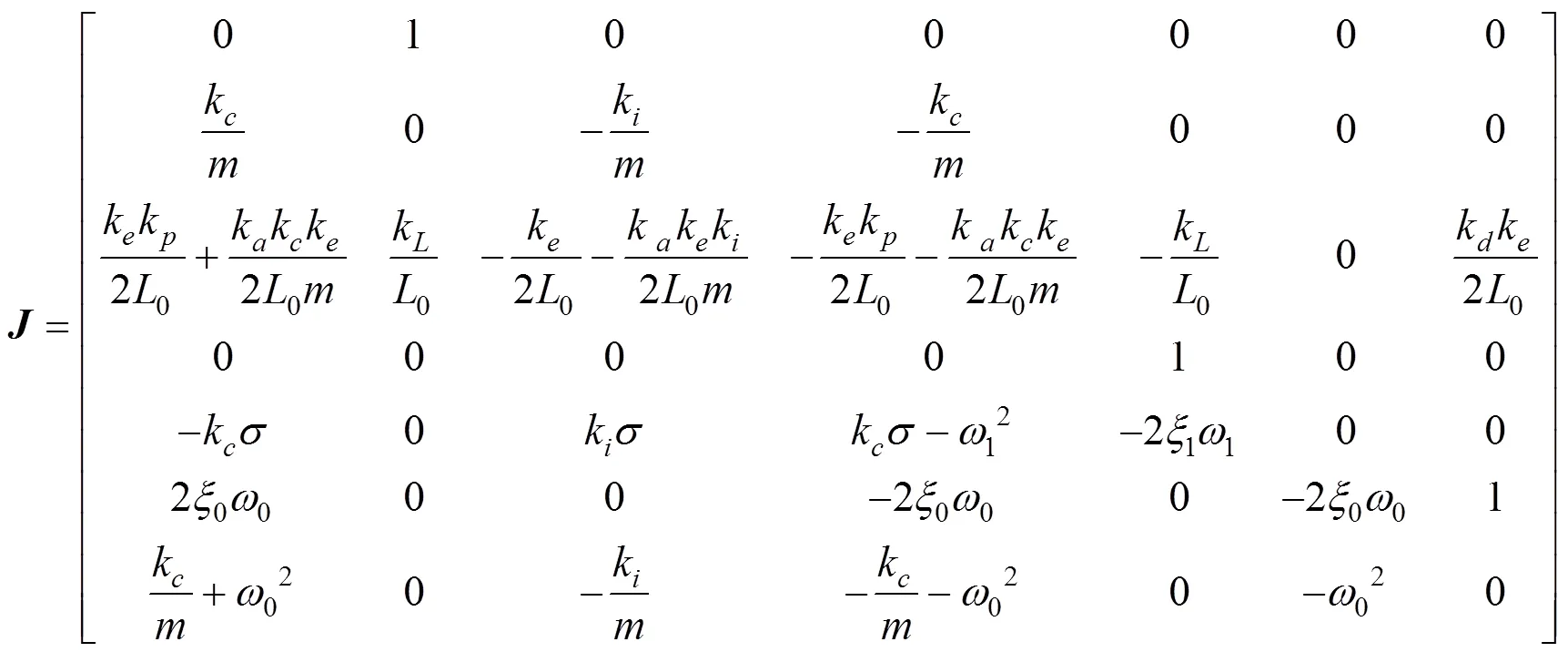
一阶线性近似的耦合系统其稳定的充要条件为系数矩阵的特征值全部分布在复平面的左半平面，即满足：

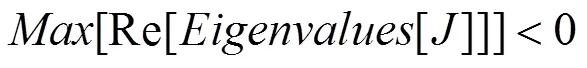
图41对耦合系统稳定性的影响

Fig. 4 Influence of1on the stability of coupled systems

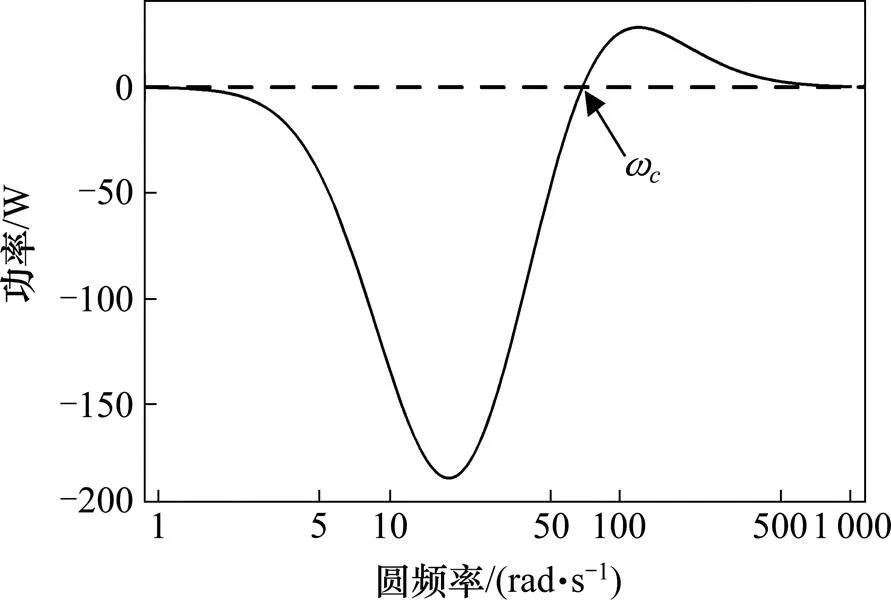
图5 悬浮系统对速度激励的输出功率曲线

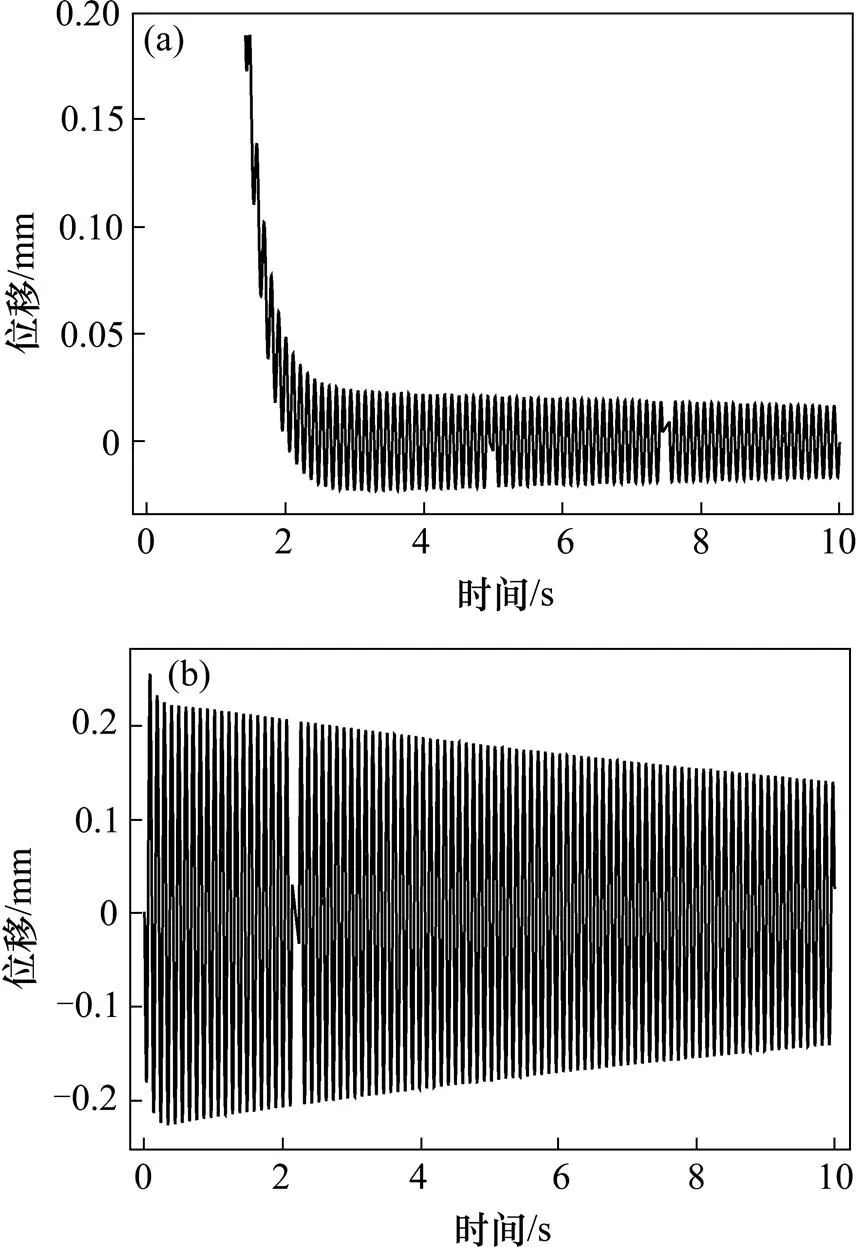
(a) 电磁铁位移；(b)轨道梁挠度

图4为耦合系统关于1的根轨迹图，随着1的增大，有1对特征根穿越虚轴使系统失稳。根轨迹与虚轴的交点，即临界频率=68.43 rad/s，图5为悬浮系统对速度激励的输出功率曲线，其临界频率=68.72 rad/s，考虑到数值计算误差，可知，即在不考虑轨道梁阻尼的情况下，控制系统可适应的轨道主频率范围，可由悬浮系统对速度激励的输出功率曲线得出，通过改变观测器参数改善悬浮系统性能的结论同样适合于耦合系统。

图6和图7为轨道梁主频率分别为60 rad/s与75 rad/s时，耦合系统的时域响应。从中可以看出，当轨道梁主频率低于临界频率时，耦合系统是稳定的；当轨道梁主频率高于临界频率时，耦合系统 发散。

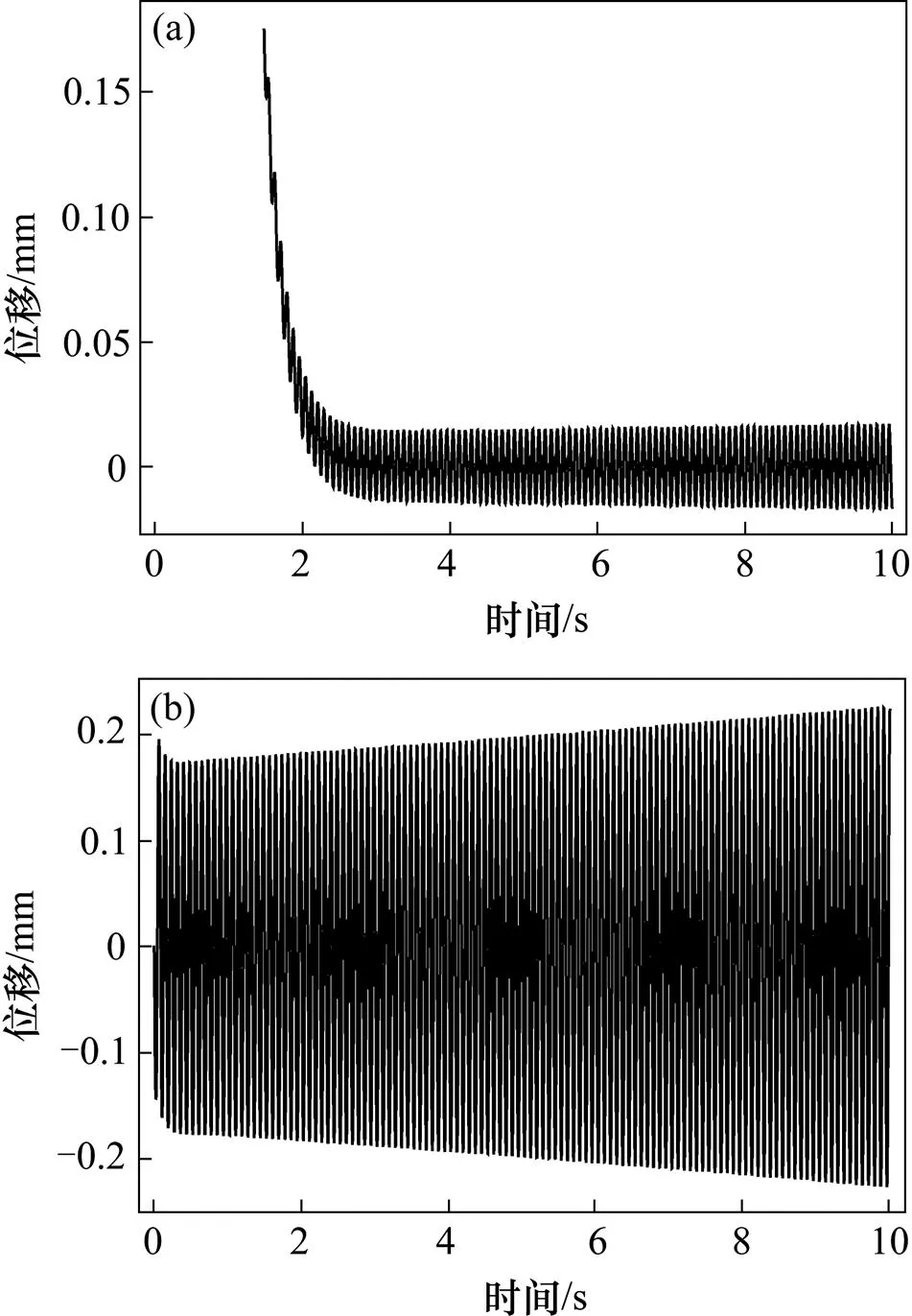
(a) 电磁铁位移；(b) 轨道梁挠度

3 结论

1) 不考虑间隙传感器微分噪声时，增大0或减小0可以显著改善系统性能，但过大的0或过小0会引入不能忽视的系统噪声，实际工程中，观测器参数应在不引入过大噪声的前提下选取较大的0与较小的0。

2) 通过耦合系统的状态空间模型得到系统关于轨道梁主频的根轨迹图，发现不考虑轨道梁结构阻尼时，令耦合系统失稳的轨道梁临界主频，与悬浮系统对速度激励的功率输出临界频率是相等的，由此得出结论，通过绘制“悬浮系统对轨道梁的振动能量输出功率”与“轨道梁主频率”间的关系曲线，即可得到不考虑轨道梁阻尼时，悬浮系统可适应轨道的临界参数。

[1] Cho H W, Han H S, Lee J M, et al. Design considerations of EM-PM hybrid levitation and propulsion device for magnetically levitated vehicle[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4632−4635.

[2] CHENG Hu, CHEN Shuwen, LI Yungang. Research on vehicle-coupled-guideway vibration in hybrid maglev system[C]// International Conference on Measuring Technology and Mechatronics Automation. IEEE, Zhangjiajie, China, 2009: 715−718.

[3] ZHOU Danfeng, Hansen C H, LI Jie, et al. Review of coupled vibration problems in EMS maglev vehicles[J]. International Journal of Acoustics & Vibrations, 2010, 15(1): 10−23.

[4] Gottzein E, Brock K H, Schneider E, et al. Control aspects of a tracked magnetic levitation high speed test vehicle[J]. Automatica, 1977, 13(3): 205−223.

[5] Yabuno H, Kanda R, Lacarbonara W, et al. Nonlinear active cancellation of the parametric resonance in a magnetically levitated body[J]. Journal of Dynamic Systems Measurement &Control, 2004, 126(3): 433−442.

[6] Alberts T E, Oleszczuk G, Hanasoge A M. Stable levitation control of magnetically suspended vehicles with structural flexibility[C]// American Control Conference. IEEE, Seattle, WA, USA, 2008: 4035−4040.

[7] LI Jinhui, LI Jie, ZHOU Danfeng, et al. Self-excited vibration problems of maglev vehicle-bridge interaction system[J]. Journal of Central South University, 2014, 21(11): 4184−4192.

[8] 梁鑫. 磁浮列车车轨耦合振动分析及试验研究[D]. 成都: 西南交通大学, 2014. LIANG Xin. Study on maglev vehicle/guideway coupled vibration and experiment on test rig for a levitation stock[D]. Chengdu: Southwest Jiaotong University, 2014.

[9] 赵春发, 翟婉明. 低速磁浮车辆导向方式及其横向动态特性[J]. 中国铁道科学, 2005, 26(6): 28−32. ZHAO Chunfa, ZHAI Wanmin. Guidance mode and dynamic lateral characteristics of low-speed maglev vehicle[J]. China Railway Science, 2005, 26(6): 28−32.

[10] 赵春发, 翟婉明. 常导电磁悬浮动态特性研究[J]. 西南交通大学学报, 2004, 39(4): 464−468. ZHAO Chunfa, ZHAI Wanming. Dynamic characteristics of electromagnetic levitation systems[J]. Journal of Southwest Jiaotong University, 2004, 39(4): 464−468.

[11] 邹东升, 佘龙华, 张志强, 等. 磁浮系统车轨耦合振动分析[J]. 电子学报, 2010, 38(9): 2071−2075. ZOU Dongsheng, SHE Longhua, ZHANG Zhiqiang, et al. Maglev vehicle and guideway coupling vibration analysis[J]. Acta Electronica Sinica, 2010, 38(9): 2071− 2075.

[12] 王洪坡, 李杰. 一类非自治位置时滞反馈控制系统的亚谐共振响应[J]. 物理学报, 2007, 56(5): 2504−2516. WANG Hongpo, LI Jie. Sub-harmonic resonances of the non-autonomous system with delayed position feedback control[J]. Acta Physica Sinica, 2007, 56(5): 2504−2516.

[13] WANG Hongpo, LI Jie, ZHANG Kun. Stability and Hopf bifurcation of the maglev system with delayed speed feedback control[J]. Acta Automatica Sinica, 2007, 33(8): 829−834.

[14] 张玲玲. 磁浮列车悬浮系统的Hopf分岔及滑模控制研究[D]. 长沙: 湖南大学, 2010. ZHANG Lingling. Research on Hopf bifurcation and sliding mode control for suspension system of maglev train[D]. Changsha: Hunan University, 2010.

[15] ZHOU D, LI J, ZHANG K. An adaptive control method to suppress the maglev track-induced self-excited vibration[C]// International Conference on Consumer Electronics, Communications and Networks. IEEE, Xianning, China, 2011: 4723−4727.

[16] 李金辉. EMS型磁浮列车—桥梁耦合振动控制技术研究[D]. 长沙: 国防科学技术大学, 2015. LI Jinhui. The vibration control technology of EMS maglev vehicle-bridge coupled system[D]. Changsha: National University of Defense Technology, 2015.

Simulation research on the effect of state observer parameters on suspension stability of maglev vehicles

LIANG Xiao1,3, MA Weihua2, XIAO Xiyue3,CHEN Xiaohao2

(1. School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China; 2. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China; 3. Hunan Maglev Technology Research Center Co., Ltd, Changsha 410000, China)

In order to solve problems of suspension instability of maglev vehicles, a coupling model of single-electromagnets and flexible track-beams was established to study on how parameters of state observers of suspension controllers affect the suspension stability of maglev vehicles. Researches about the transfer function of suspension systems were conducted and gotten some impressive results, such as curves that plot the relationship between the frequency of speed excitation signals and the power output of the suspension system to track-beams, influence rules that parameters of state observers affect system performance of maglev vehicles and so on. Based on the study about the change rule of state-space model of the coupling system, a conclusion is drawn that it is possible to analysis critical parameters of track-beams, which suspension system can be adapted to.

suspension system; transfer function; power output; critical frequency

10.19713/j.cnki.43−1423/u.2019.04.025

U270.2

A

1672 − 7029(2019)04 − 1026 − 07

2018−05−28

湖南省科技重大专项资助项目(2015GK1001)；国家社会科学基金青年基金资助项目(16CGL004)；国家自然科学基金面上资助项目(51875483)；四川省重点研发资助项目(2018GZ0054)

马卫华(1979−)，男，山东滕州人，副研究员，博士，从事机车车辆系统动力学、磁浮列车走行机构研究；E−mail：mwh@swjtu.edu.cn

(编辑 阳丽霞)