基于可靠度的列车多部件预防性机会维修策略研究

肖红升，贺德强, 2，杨严杰，苗剑



基于可靠度的列车多部件预防性机会维修策略研究

肖红升1，贺德强1, 2，杨严杰1，苗剑1

(1. 广西大学 机械工程学院，广西 南宁 530004； 2. 广西制造系统与先进制造技术重点实验室，广西 南宁 530004)

针对现行轨道车辆检修模式存在过维修和欠维修等问题，提出基于可靠度的列车多部件预防性维护策略。引入故障率递增因子和役龄递减因子，采用维修与更换相结合的维护方式，依据可靠性要求确定单部件最佳预防性维修周期及维修次数。通过分析部件之间维修的经济相关性，在单部件最佳预防性维修周期基础上，通过二次抛物线插值法优化机会维修可靠度阈值，使总维护费用最少，从而得到最优机会维修可靠度。研究结果表明：相比于传统列车维修策略，运用提出的预防性机会维修策略，在保障列车可靠性的同时可减少入库检修次数，节省维护费用，保证了列车运行的安全性和维修的经济性。

轨道车辆；可靠性；多部件；预防性维修；机会维修

近年来，我国轨道交通事业获得了快速的发展，轨道车辆作为轨道交通系统的重要组成部分，保障其安全高效地运行具有重要意义。目前，我国轨道交通列车的检修主要采用定期计划维修和故障维修相结合的检修模式，易出现维修不足和维修过剩等问题，不能充分保证列车的安全运行，同时也造成一定的维修资源浪费。针对现行轨道车辆检修模式存在的不足，不少学者在以可靠性为中心的列车检修模式方面进行了积极地探索。王华胜等[1−2]针对我国轨道车辆的运营与维修情况，提出了列车零部件现场数据的收集与处理方法，并建立了车辆零部件的三参数威布尔分布模型。刘志龙等[3]综合考虑设备故障维修的经济性与方便性，提出了基于故障效费比的分析方法，获得地铁车辆设备的最佳预防性维修时机，使设备的使用价值最大化。王红等[4−5]基于现行的地铁列车维护模式，提出了定期保养，不定期维修与更换相结合的地铁列车维护决策模型；同时考虑了故障风险对动车组维修经济性与运行安全性的影响并建立了决策模型。以上研究都是针对列车单部件而进行的维修决策优化，轨道交通列车是一个复杂的机电设备，各部件之间存在复杂的经济相关性、结构相关性和随机相关性[6]，建立维修决策模型时需考虑部件的各种相关性，实施一定程度的多部件联合维修，更加符合工程实际。Lung等[7−8]根据系统部件之间的各种相关性，将多部件维修分为成组维修、分组维修和机会维修。机会维修是考虑系统部件之间维修的经济相关性，将故障发生时机邻近的多个部件，联合进行维修，以降低总维修费用。胡瑾秋等[9]综合分析复杂油气设备各个部件之间的故障相关性及经济相关性，提出了一种基于故障超前防御的全局优选机会维护模型。ZHANG等[10]将机会维修的思想用于风电机组的维修，对多个部件进行联合维修，分摊高额固定维修费用。本文以轨道车辆现有检修模式为基础，引入机会维修的思想，采用故障修、预防性维修、机会维修、更换维修相结合的维修方式，以可靠度为约束，部件机会维修可靠度阈值为决策变量，单位时间内的总花费最少为目标函数，建立列车多部件预防性机会维修模型。通过设置合理的机会维修阈值，在列车一次停运检修时，让尽可能多的部件进行维修，以减少列车停运次数，从而节省列车总的维修费用。

1 基于可靠度的预防性机会维修策略原理

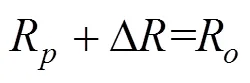
2 基于可靠度的列车预防性机会维修策略

2.1 列车预防性维护模型假设

目前，轨道列车的检修模式主要采用定检定修的计划维修以及少部分的状态维修。修程修制的制定是根据多年的运营维修经验，缺乏对部件失效数据的有效分析，存在一定程度的欠维修和过维修，影响列车的行车安全及造成维修资源的浪费。为了保证列车预防性机会维修模型的通用性，建模时做出如下假设：

1) 列车作为大型运输车辆，将运营距离 (万km)作为维修周期更加合理。，的单位均为 万km；

2) 所有列车车载设备均从全新状态开始运行，即初始故障率为0；

3) 所有列车车载设备服从适应性较强的二参数威布尔分布；

4) 列车车载设备在预防性维修前出现的故障采用小修，使设备故障率恢复到故障前状态，即“恢复如旧”。预防性维修使设备处于“恢复如旧”与“恢复如新”之间。更换维修使部件“修复 如新”；

5) 列车车载设备的状态检测在日常的保养维护中完成，不占用额外的时间。

2.2 列车单部件最佳预防性维护模型研究

现行的轨道列车检修是采用等周期的预防性维修，然而设备的预防性维修不能使设备修复如新，周期性的预防性维护会使设备可靠度逐步降低，采用等周期的预防性维修不可避免地会出现过维修和欠维修，为了保证设备的可靠性，应该实施更频繁的预防性维修[11]。为了表达每一次预防性维修对设备可靠度的影响，引入役龄递减因子和故障递增因子[12]，则非完备预防性维护的故障率随着维修次数的增多故障率逐渐增大，对于非完备维修在进行一定次数的预防性维修，应进行更换维修使部件恢复如新，使维护更加经济。 故障率递推函数如下：

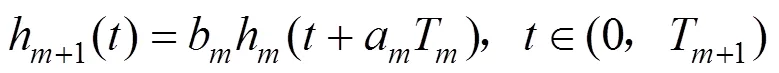
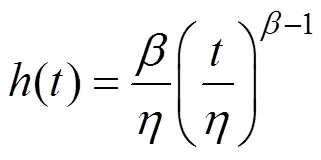
式中：为部件的形状参数；为特征寿命参数，，可通过对部件的历史失效数据统计分析得到。根据故障率函数可得列车车辆部件每个维修阶段的可靠度函数：

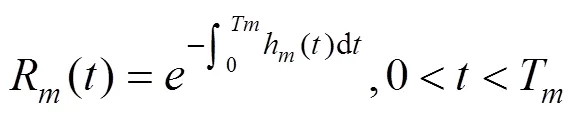
为了保证列车可靠运行，每个车载设备都有保证列车安全运行的最低可靠度R，根据可靠性原理有

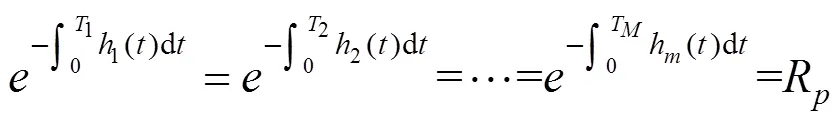
联立式(1)~(4)可解得每次单部件最佳预防性维修周期，根据设备维修之间的经济相关性，设备的最佳维护次数可根据单位时间内维护费用最少即式(6)求得，维护费用主要包括故障小修、预防性维修和更换维修3个部分，故障小修次数可用维修间隔内的累积故障率表示，则总故障次数等于每个预防性维修周期内累积故障率之和，如式(5)所示。

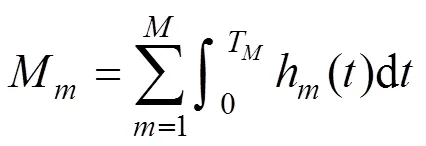
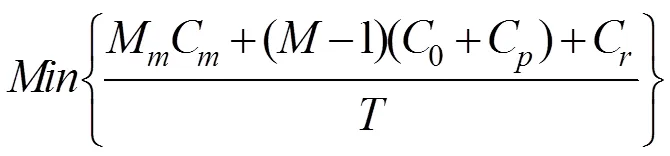
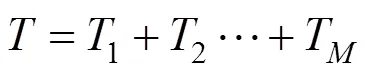
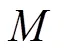
2.3 列车多部件预防性机会维护模型研究

单部件最佳预防性维护决策确定后，以单部件预防维修周期为基础，引入机会维修思想，设置适当的机会维修阈值，将处于机会维修区域的部件与正在进行预防性维修的部件联合进行维修，减少列车入库检修的次数。

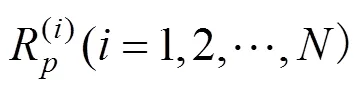
2.3.1 目标函数

本文主要是考虑部件之间的经济相关性，将预防性维修时机相近的部件进行联合维修，以减少维修费用，因此以所有考察部件单位里程内的总的维护费用最少为目标函数。

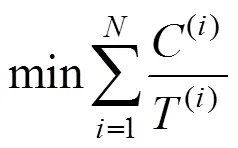
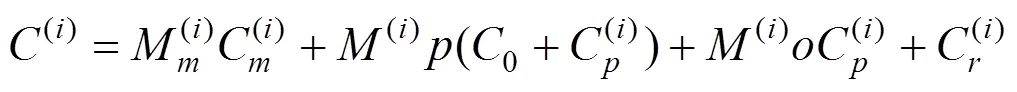
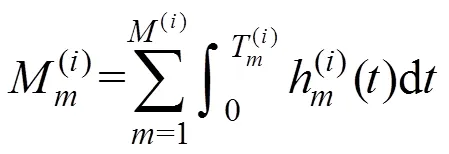
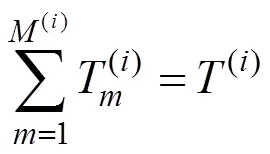
2.3.2 决策变量

2.3.3 约束条件

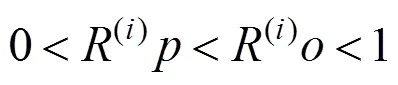
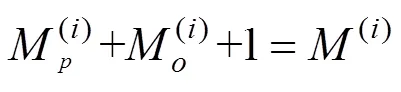
预防性机会维修模型如下：

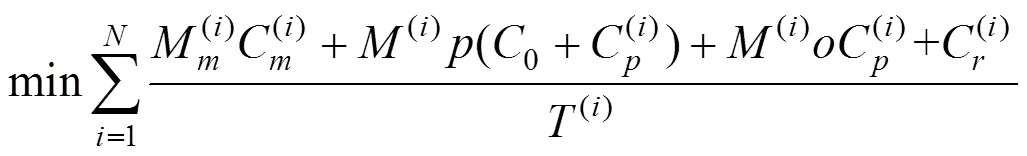
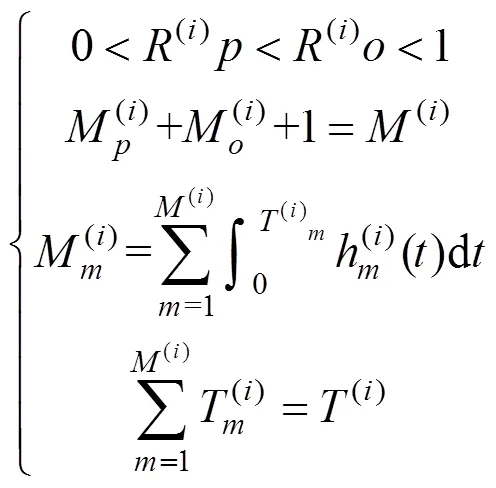
3 轨道列车预防性机会维护模型求解

本文建立的优化模型是一个多参数非线性的优化问题，模型求解步骤如下。

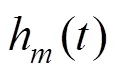
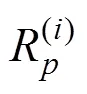
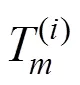
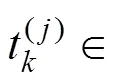
6) 计算部件的下一次维修时间，若部件此次进行的是预防性维修，则下一次预防性维修时 间为：

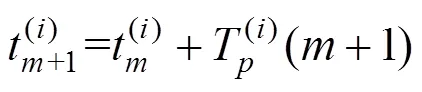
如果部件此次进行的是机会维修且给其机会维修机会的部件为，则下一次预防性维修时间为：

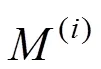
4 算例分析

通过对地铁列车转向架部件历史故障数据进行统计分析，可得到各部件的失效率函数。以转向架系统的轴箱定位装置、中央悬挂及牵引、牵引电机轴箱和轮对4个部件为研究对象，并对其进行编号，验证提出模型的有效性。参照文献[13]部件各参数的设置如表1，假设各部件同一维修阶段的役龄递减因子和故障率递增因子相等，且为：

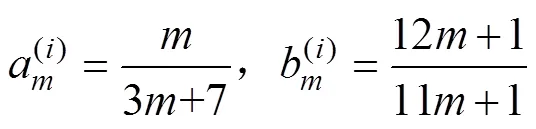
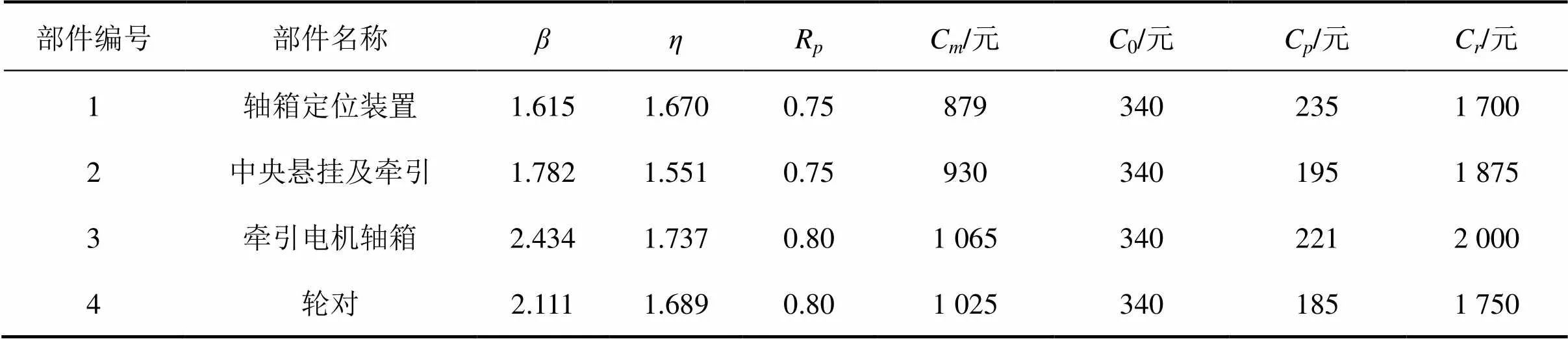
表1 部件参数设置表

4.1 部件最佳预防性维修次数

由非完备维修故障率的变化规律可知，随着预防性维修次数的增加，维修间隔将逐步变短，维修经济性将变差，所以进行一定次数的预防性维修后需进行预防性更换。根据式(6)单位里程内花费最少为目标函数，以维修次数为决策变量。单位里程内总维护费用与维修次数的关系如图2所示，可以看出各部件单位里程内的维护费用变化趋势基本一致，在更换次数较少时，费用较高，表明新部件在刚开始运行时，对其进行预防性维修可使可靠度保持在较高水平，实施更换不经济。随着预防性维修次数的增多故障率增长较快，恢复相当的可靠性水平需付出更大代价，所以为了保持维修的经济性，部件进行一定次数的预防性维修时需对其进行更换维修。从图2可以看出，各部件均在第4次预防性维修时，单位里程的花费最少，即在第4次预防性维修时进行预防性更换维修。

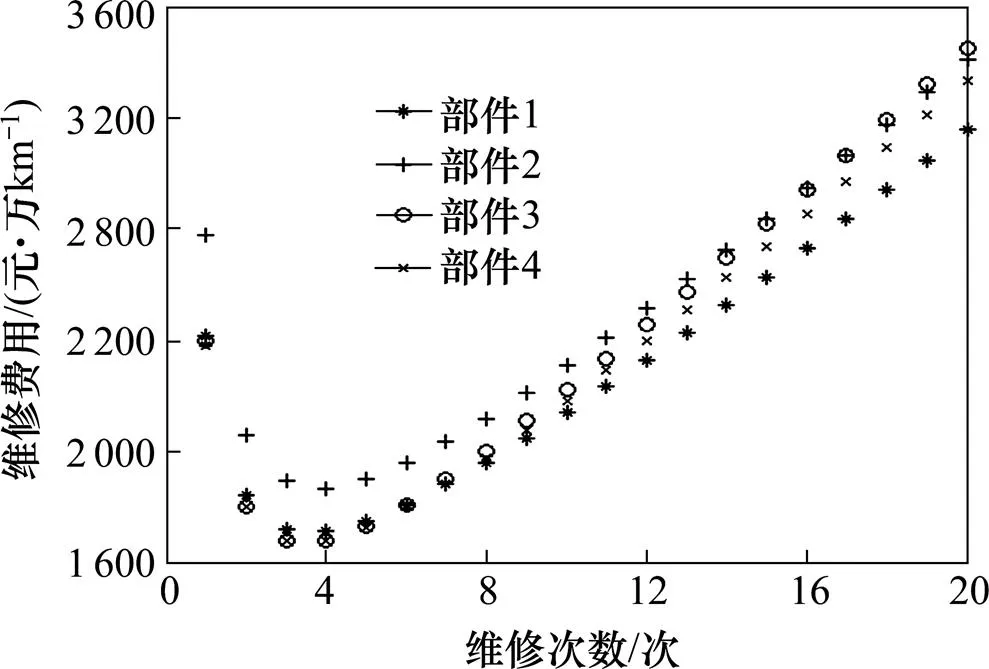
图2 单位里程的维修费用与维修次数的关系图

4.2 机会维修可靠度阈值分析

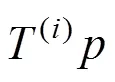
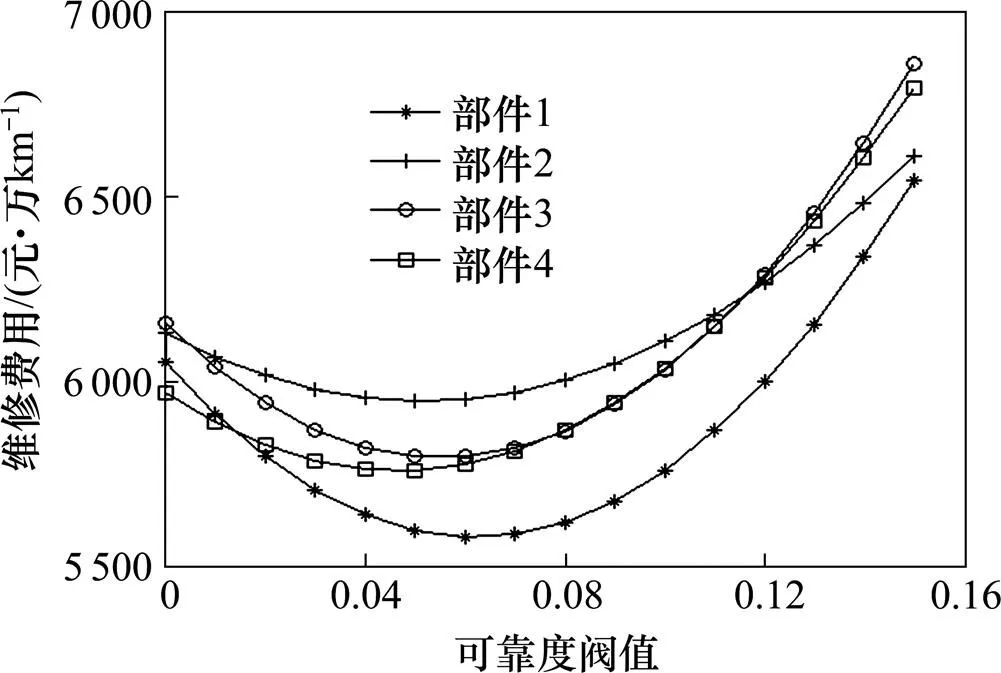
图3 维修费用与机会维修阈值的关系

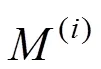
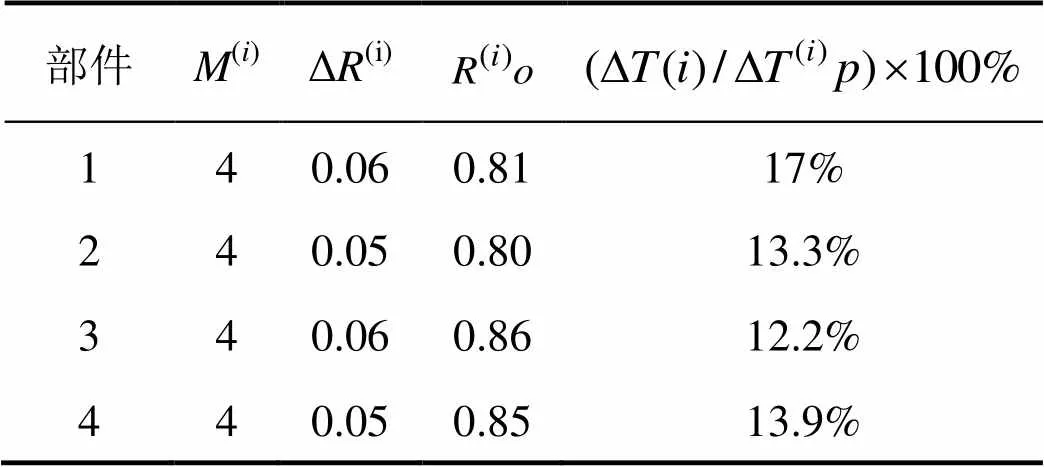
表2 预防性机会维修参数优化结果

4.3 基于可靠度的列车机会维修策略优化结果

表2给出了机会维修各项参数，根据式(3)可求出各部件的预防性维修里程及机会维修里程。在一个更换里程内，各部件单部件顺序维修策略和多部件联合机会维修决策分别如图4和图5所示。从图中可以看出一个换检修周期内，进行单部件的预防性维修要进行16次检修，而采用机会维修策略仅需10次检修。

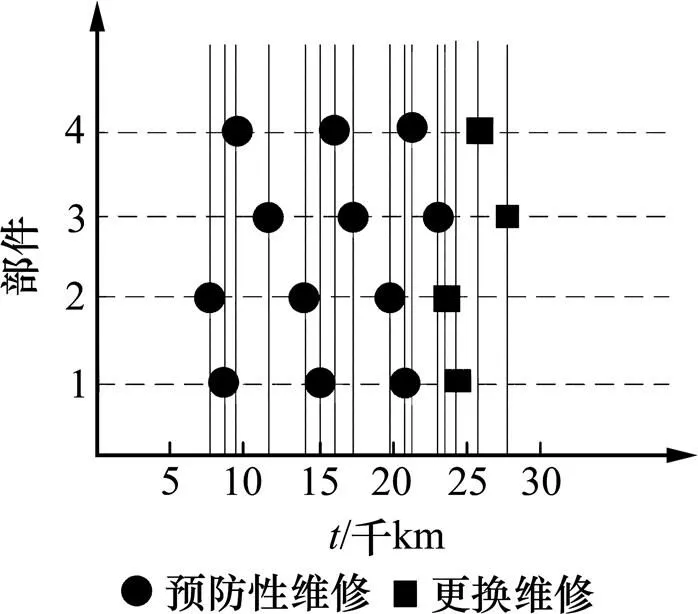
图4 单部件预防性顺序维修决策

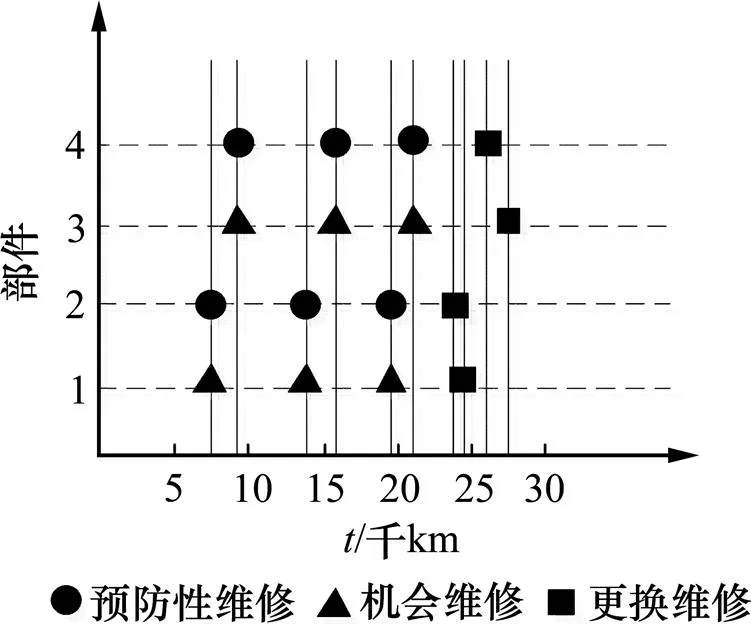
图5 多部件机会维修决策

表3 2种维修决策结果对比

以城市轨道交通列车年检里程(约12万km)为例，分析单个转向架4部件采用预防性机会维修策略与传统预防性维修维修的费用，比较结果如表3所示。从表3可以看出，采用预防性机会维修策略，一个年检周期内共停车检修25次，维修费用62 827元，采用单部件预防性维修需停车检修50次，维修费用73 159元，采用预防性机会维修的费用节省率达14.12%。假设某地铁公司共有35辆B型地铁列车，均采用4动2拖的编组形式，每列车有轴箱及定位装置4套，中央悬挂牵引装置6套、牵引电机轴箱4个、轮对12对，则该地铁公司对所有列车同一类部件采用预防性机会维修策略，一个年检周期可内节约156.04万元。

由上述分析可知，列车各部件实施一定程度的机会维修，可减少列车停车检修次数，分摊固定维修费用，节约总的维修费用，证明了基于可靠度的列车多部件预防性机会维修模型的有效性和经 济性。

5 结论

1) 采用基于可靠度的列车多部件预防性机会维修策略，在保证部件安全运行的同时可减少列车停车检修次数，以及车辆段的配属车辆数，从而节省总的维护费用，保证列车运行的安全性和维修的经济性。

2) 采用多种维修与更换相结合的维护方式以适应列车机电设备的多种故障形式，模型具有较好的鲁棒性。

3) 针对传统列车检修模式在安全性和经济性上存在的不足，综合考虑部件维修之间的经济相关性，引入机会维修思想，提出了基于可靠度的列车多部件预防性机会维修策略。通过仿真分析，确定最佳机会维修区域占预防性维修区域15%左右，维修节约率达14.2%，证明了维修决策具有一定的可行性，可为列车的检修优化提供理论依据。

[1] 王华胜. 基于加权最小二乘法的机车车辆零部件可靠性分析[J]. 铁道学报, 2001, 23(6): 21−25. WANG Huasheng. Reliability analysis of locomotive and car parts based on weighted least squares method[J]. Journal of the China Railway Society, 2001, 23(6): 21−25.

[2] 王灵芝, 徐宇工, 张家栋. 铁路设备关键零部件的可靠性分析模型及其应用研究[J]. 铁道学报, 2008, 30(4): 93−97. WANG Lingzhi, XU Yugong, ZHANG Jiadong. Reliability analysis model of key parts of railway equipment and its application research[J]. Journal of the China Railway Society, 2008, 30(4): 93−97.

[3] 刘志龙, 王红, 杜维鑫, 等. 基于效费比的地铁车辆设备预防性维护决策优化[J]. 铁道科学与工程学报, 2016, 13(1): 146−151. LIU Zhilong, WANG Hong, DU Weixin, et al. Preventive maintenance decision optimization for metro vehicle equipment based on cost-effective[J]. Journal of Railway Science and Engineering, 2016, 13(1): 146−151.

[4] 王红, 刘志龙, 杜维鑫, 等. 基于多种维护方式的地铁车辆设备预防性维护策略及维护模型[J]. 中国铁道科学, 2016, 37(4): 108−114. WANG Hong, LIU Zhilong, DU Weixin, et al. Preventive maintenance strategy and maintenance model of metro vehicle equipment based on multiple maintenance modes [J]. China Railway Science, 2016, 37(4): 108−114.

[5] 王红, 熊律, 杜维鑫, 等. 考虑故障风险的动车组部件预防性维护优化建模[J]. 机械工程学报, 2016, 52(24): 123−129. WANG Hong, XIONG Lü, DU Weixin, et al. Optimal modeling for preventive maintenance of EMU components considering fault risk[J]. Journal of Mechanical Engineering, 2016, 52(24): 123−129.

[6] 郭建, 徐宗昌, 孙寒冰. 基于比例风险模型的装备机会维修阈值优化[J]. 计算机集成制造系统, 2017, 23(12): 2622−2629. GUO Jian, XU Zongchang, SUN Hanbing. Opportunistic maintenance threshold optimization of equipment based on proportional hazard model[J]. Computer Integrated Manufacturing Systems, 2017, 23(12): 2622−2629.

[7] Lung B, Do P, Levrat E. Opportunistic maintenance based on multi-dependent components of manufacturing system[J]. CIRP Annals-Manufacturing Technology, 2016(65): 401−404.

[8] HOU W R, JIANG Z H. An opportunistic maintenance policy of multi-unit series production system with consideration of imperfect maintenance[J]. Applied Mathematics & Information Science, 2013(7): 283−290.

[9] 胡瑾秋, 张来斌. 基于故障超前防御的复杂油气生产设备机会维护模型[J]. 机械工程学报, 2013, 49(12): 167−175. HU Jinqiu, ZHANG Laibin. The opportunity maintenance model of complex oil and gas production equipment based on fault ahead defense[J]. Journal of Mechanical Engineering, 2013, 49(12): 167−175.

[10] ZHANG Chen, GAO Wei, GUO Sheng, et al. Opportunistic maintenance for wind turbines considering imperfect, reliability-based maintenance[J]. Renewable Energy, 2017(103): 606−612.

[11] Pandey M, ZUO M J, Moghaddass R, et al. Selective maintenance for binary systems under imperfect repair[J]. Reliability Engineering & System Safety, 2013(113): 42−51.

[12] ZHOU Xiaojun, LU Zhiqiang, XI Lifeng, et al. Opportunistic preventive maintenance optimization for multi-unit series systems with combing multi-preventive maintenance techniques[J]. Journal of Shanghai Jiaotong University (Science), 2010, 15(5): 513−518.

[13] 孙超. 基于可靠性分析的轨道交通车辆转向架维修周期研究[D]. 南京: 南京理工大学, 2014. SUN Chao. Research on maintenance cycle of rail vehicle bogie based on reliability analysis[D]. Nanjing: Nanjing University of Science and Technology, 2014.

Research on the preventive opportunistic maintenance strategy of train multi-components based on reliability

XIAO Hongsheng1, HE Deqiang1, 2, YANG Yanjie1, MIAO Jian1

(1. College of Mechanical Engineering, Guangxi University, Nanning 530004, China; 2. Key Laboratory of Guangxi Manufacturing System and Advanced Manufacturing Technology, Nanning 530004, China)

In view of the problems of over-maintenance and under-maintenance in the existing maintenance mode of rail vehicles, the preventive maintenance strategy of train multi-components was put forward based on reliability. The failure increasing rate factor and age reduction factor were introduced and the combined maintenance mode of maintenance and replacement was used to get the best single-component maintenance cycle and the number of preventive maintenances according to reliability requirements. In order to get the least total maintenance cost and the optimal opportunistic maintenance reliability, the opportunistic maintenance reliability threshold was optimized by two parabola interpolation method based on the optimal preventive maintenance cycle of single-component. It shows that preventive opportunistic maintenance strategy can keep safe reliability and reduce the number of parking repairs and maintenance costs compared with single-component preventive maintenance strategy. The safety of the train operation and the economy of maintenance are guaranteed.

rail vehicles; reliability; multi-components; preventive maintenance; opportunistic maintenance

10.19713/j.cnki.43−1423/u.2019.04.026

TP391.9；U260

A

1672 − 7029(2019)04 − 1033 − 08

2018−06−05

国家自然科学基金资助项目(51765006)；广西自然科学基金重点资助项目(2017JJD150010)；广西制造系统与先进制造技术重点实验主任课题资助项目(15-140-30S003)；广西研究生教育创新计划资助项目(YCSW2018033)

贺德强(1973−)，男，湖南桃江人，教授，博士，从事列车故障诊断与智能维护、列车网络与控制、网络化制造等研究；E−mail：hdqianglqy@126.com

(编辑 蒋学东)