类Exechon并联机构模块可重构概念设计与运动学分析

汤腾飞，方汉良，张 俊



类Exechon并联机构模块可重构概念设计与运动学分析

汤腾飞，方汉良，张 俊

(福州大学机械工程及自动化学院，福州 350116)

可重构与模块化设计是实现并联机构多功能、提升装备加工柔性的关键技术. 受商用Exechon并联机构模块优异性能的设计启发，在其变异机构Exe-Variant的基础上，应用机构变异思想提出两种类Exechon并联机构模块——Exe-Ⅰ和Exe-Ⅱ. 基于可锁定关节、模块化支链以及可重构并联机构的设计思路，依次开展Exechon、Exe-Variant、Exe-Ⅰ和Exe-Ⅱ等4种类Exechon并联机构的模块化、可重构概念设计. 针对以上并联机构模块进行运动学分析：运用螺旋理论分析类Exechon并联机构的系统螺旋系，构建类Exechon并联机构的系统全雅克比矩阵，依次分析机构自由度和奇异性；通过矢量闭环方程推导其逆运动学模型和动平台连带运动；以“分层切片”的工作空间搜索方法预估其工作空间. 运动学对比分析表明：对类Exechon并联机构模块开展的可重构设计，保留了并联机构的自由度类型和结构奇异性特征，并显著改善了部分类Exechon并联机构的逆运动学连带运动的复杂程度以及动平台可达工作空间的分布. 最后，借助3D打印技术制作了Exe-Ⅰ并联机构模块的原理样机，运动学精度实验结果与理论分析结果吻合较好，数据的绝对误差在±0.4mm以内，并且其相对误差不大于实验值的3.2%，验证了运动学分析的正确性. 本文提出的可重构与模块化概念设计，可为类Exechon并联机构模块的高效可重构设计及其工程应用提供关键技术支撑.

并联机构；可锁定关节；可重构；运动学

少自由度并联机构因其高精度、高刚度、低惯量以及结构紧凑等优点，在机械加工、分拣搬运以及医疗康复等领域受到广泛的关注[1-3]．作为少数业已成功商用的并联机构之一，Exechon并联机构以其拓扑结构简单、关节数目少(仅13个单自由度关节)以及过约束设计等优点[4]，实现了优异的精度和刚度性能，为精密制造，特别是高性能航空结构件的加工提供了一种技术解决方案[5-6]．

以机构学观点分析，Exechon并联机构模块为一拓扑构型2UR&1SR(U表示虎克铰，表示移动副，R表示转动副，S表示球铰)的机构，而通过机构变异得到的类Exechon型Exe-Variant并联机构模块为一拓扑构型2RU&1RS的机构[7]．比较Exechon和Exe-Variant可知，两种并联机构具有相同的运动副类型和相似的支链配置，仅在运动副的布置上存在差异.沿用此种机构变异方法，通过对以上并联机构的运动副进行重新布置，可构造两种新的类Exechon并联机构，分别命名为Exe-Ⅰ和Exe-Ⅱ，其拓扑构型为2UR&1RS和2RU&1SR．

关于Exechon并联机构模块及其变异机构的研究主要集中于尺度综合[8-9]、运动学分析[10-12]、静刚度设计[13-14]、动力学分析[15-16]等方面.然而，市场需求的快速转变对制造装备的加工柔性提出了严苛要求[17].可重构与多功能作为并联机构的重要发展趋势[18]，也是实现并联机构加工柔性的关键技术.因此，亟需开展类Exechon并联机构模块的可重构设计，以提升该类并联装备应对多样化加工任务的能力.

可重构机构的设计思想在于通过一个复合的或集成的机械系统实现多任务需求下的不同配置[19].可重构并联机构因为兼具传统固定构型并联机构的高刚度、高精度、低惯量和紧凑结构的优点，以及可重构机构应对多工况、多任务和多功能需求的快速重构特性，成为机构学领域的研究热点之一.当前，可重构并联机构的设计主要基于变胞运动副[20-22]、变胞机构[23]、可锁定关节[24-26]、运动转向机构[27]和运动限定机构[28]的设计.Dai等相继提出了含多个子态结构的rT型、vA型和rR型变胞运动副[20-22]，并将其应用于可重构的变胞并联机构的设计[23].基于可锁定关节的设计，Kong等[24]进一步分析了一类3自由度可重构并联机构的构型综合问题.Palpacelli等[25]将具有转轴可重构能力的球关节应用于并联机构的开发.Carbonari等[26]提出了一系列具有3-CPU(C表示圆柱副)构型的可重构并联机构.与上述通过可锁定关节实现机构可重构的设计不同，Kong等[27]研究了具有两种操作模式的运动转向机构.叶伟等[28]以可重构混联运动支链为设计基础，构造了具有多种工作模式的可重构并联机构.

需要指出的是，在机构可重构与模块化设计基础上，系统地开展运动学分析是又一关键性设计工作.为此，本文以4种类Exechon并联机构模块为研究对象，开展如下研究工作：首先以笔者前期提出的可锁定关节[29]为基础，开展4种类Exechon并联机构模块的可重构概念设计；然后依次分析类Exechon并联机构模块的自由度、奇异性、逆运动学和工作空间，并定性分析了可重构设计对其运动学性能的影响；最后借助3D打印技术，制作Exe-Ⅰ并联机构模块的原理样机，通过设计运动学精度实验验证上述运动学分析的正确性.希冀通过类Exechon并联机构模块的可重构概念设计和运动学分析，为该类并联机构的加工柔性设计以及模块化工程应用提供基础理论指导.

1 可重构概念设计

1.1 可锁定关节

如图1所示，笔者提出的两类可锁定球关节(lockable spherical joint，LSJ)，可分别布置于类Exechon并联机构模块的动平台和运动支链(LSJ-Ⅰ)以及静平台和运动支链(LSJ-Ⅱ)之间，增强该并联机构的可重构性.

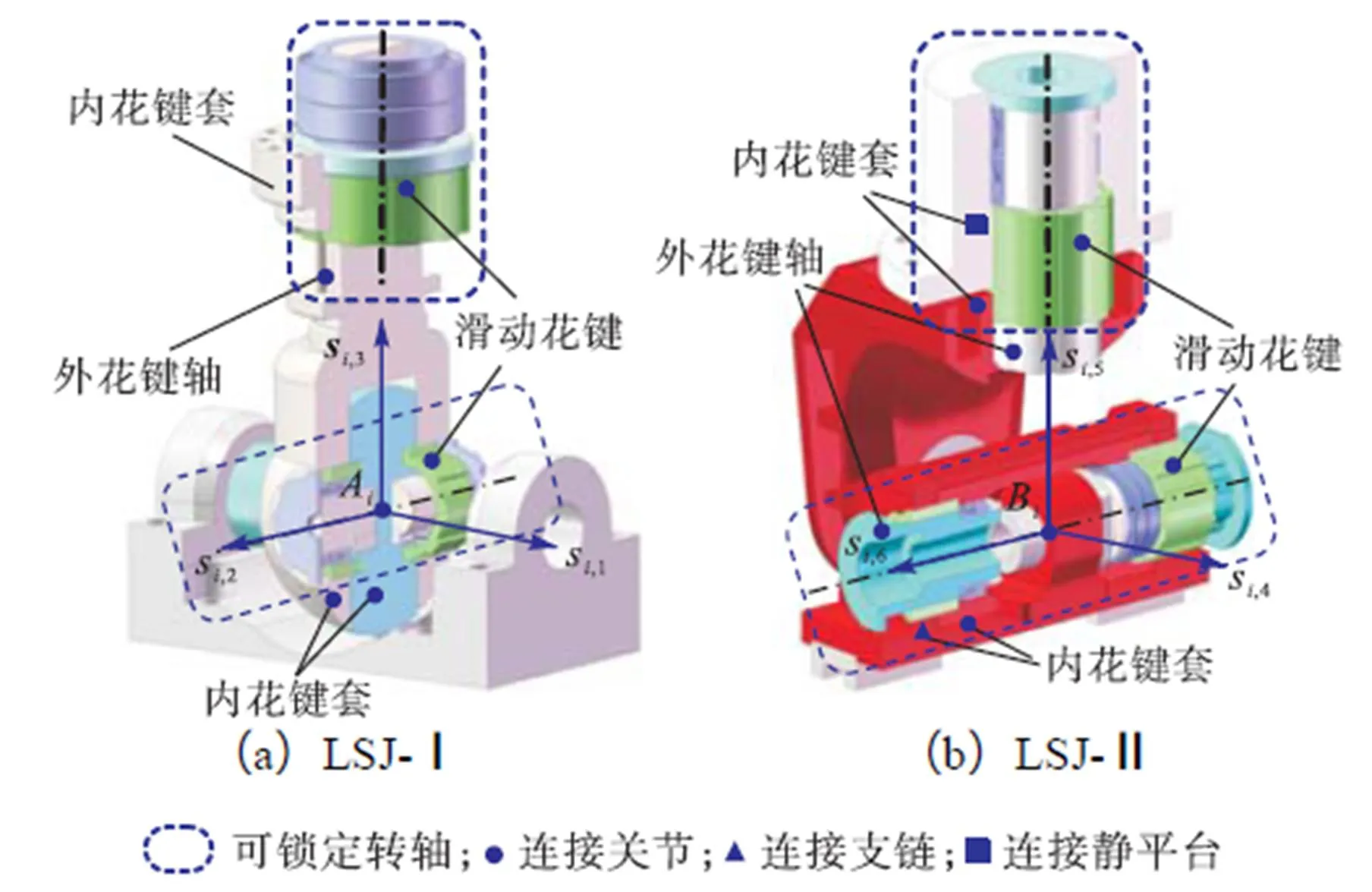
图1 可锁定关节剖面结构

以上可锁定球关节的锁定与解锁过程如图2 所示．

图2 可锁定球关节的锁定与解锁状态转换示意

以上解锁和锁定的动作均需要在光电位置标记点和′(图2(a))检测重合后，再由集成于滑动花键和外花键轴的电磁驱动器(图2(b))实现动作.此外，电磁驱动器将在可锁定转轴不动作时对滑动花键进行制动，以保持以上动作位置的精确.

执行以上可锁定转轴的锁定与解锁动作，可分别实现两类可锁定球关节的关节重构，得到与其对应的R、U和S副.表1所示为可锁定球关节LSJ-Ⅰ和-Ⅱ重构的关节类型.

1.2 模块化支链

以两类可锁定球关节LSJ-Ⅰ和LSJ-Ⅱ为基础，集成导轨组件、丝杠-螺母、伺服电机和支链体等模块，可实现模块化运动支链的概念设计，如图3所示.

图3中，可锁定球关节LSJ-Ⅰ和LSJ-Ⅱ可分别重构成R、U和S副，并作为从动运动关节分别连接支链体和动、静平台。此外，伺服电机作为支链体的动力输入，用于连接丝杠-螺母，并驱动导轨组件(副).通过组合不同的可锁定球关节的关节配置，可形成移动副驱动的模块化支链，用以满足不同拓扑构型的类Exechon并联机构模块设计方案.

表1 可锁定球关节重构的关节类型

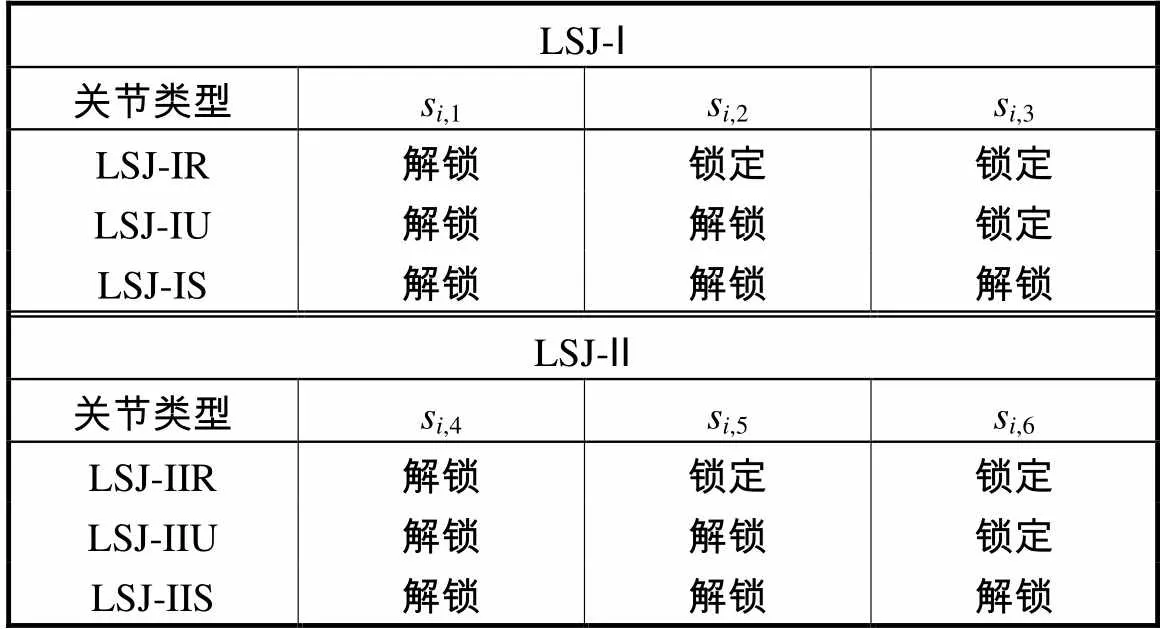
Tab.1 Various joints reconfiguring from LSJs

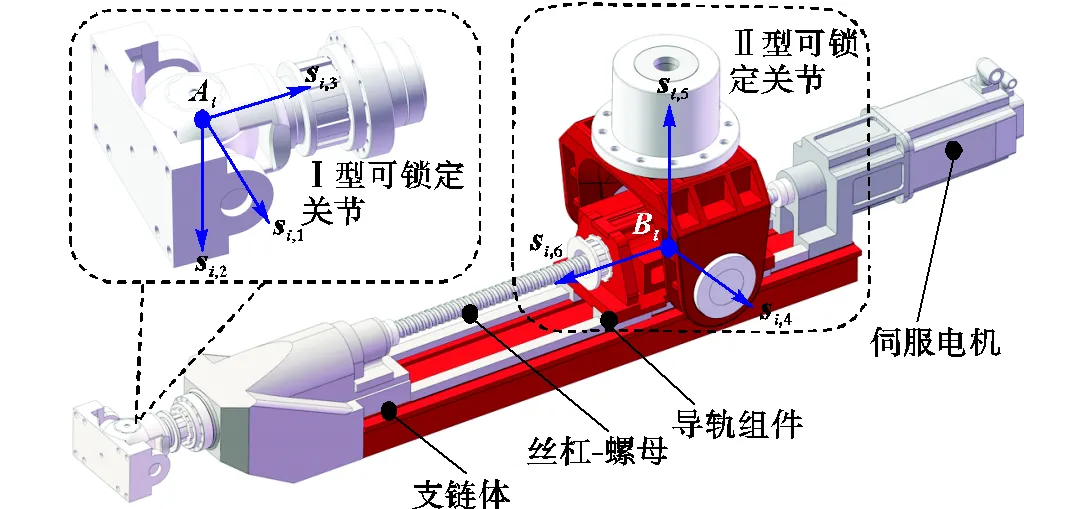
图3 模块化运动支链结构示意

1.3 可重构并联机构

如图4所示，将第1.2节的模块化运动支链(含伺服驱动)与静平台、动平台(含电主轴)相结合，即可实现类Exechon并联机构模块的可重构概念设计.

图4中，A和B点分别表示与动、静平台相连接的可重构关节的关节转动中心，C(＝1，2，3)点表示支链后端轴承的旋转中心；和点分别表示动、静平台的几何中心；位于动、静平台的△123和△123均构成等腰直角三角形，且直角为∠2＝∠2＝90°．如图4所示，具有可重构功能的类Exechon并联机构模块可根据选定的机构拓扑构型，确定各个模块化运动支链上的可锁定关节配置，在单一机构上实现多种同类构型的快速转换，并通过各支链上伺服电机的驱动，实现动平台末端的期望运动输出，满足多样化的工程应用需求．

以下简要说明类Exechon并联机构模块Exechon和Exe-Variant的可重构设计．

如图5(a)所示，与动平台相连的可锁定球关节设置为R副(LSJ-ⅠR)，而与静平台相连的可锁定球关节分别设置为U副(LSJ-ⅡU)和S副(LSJ-ⅡS)，即Exechon并联机构模块由3条拓扑构型分别为UR和SR的模块化运动支链并联构成．类似地，如图5(b)所示，与动平台相连的可锁定球关节分别设置为U副(LSJ-ⅠU)和S副(LSJ-ⅠS)，而与静平台相连的可锁定球关节设置为R副(LSJ-ⅡR)，即Exe-Variant并联机构模块由3条拓扑构型分别为RU和RS的模块化运动支链并联构成．

借助机构变异方法，对Exechon和Exe-Variant并联机构模块进行构型重构，可得到如图6所示的类Exechon并联机构模块Exe-Ⅰ和Exe-Ⅱ．

图4 可重构类Exechon并联机构模块概念设计

图5 Exechon和Exe-Variant并联机构的可重构设计方案

图6 两种类Exechon并联机构的可重构设计方案

如图6(a)所示，与动平台相连的可锁定球关节分别设置为R副(LSJ-ⅠR)和S副(LSJ-ⅠS)，而与静平台相连的可锁定球关节分别设置为U副(LSJ-ⅡU)和R副(LSJ-ⅡR)，即Exe-Ⅰ并联机构模块由3条拓扑构型分别为UR和RS的模块化运动支链并联构成．类似地，如图6(b)所示，与动平台相连的可锁定球关节分别设置为U副(LSJ-ⅠU)和R副(LSJ-ⅠR)，而与静平台相连的可锁定球关节分别设置为R副(LSJ-ⅡR)和S副(LSJ-ⅡS)，即Exe-Ⅱ并联机构模块由3条拓扑构型分别为RU和SR的模块化运动支链并联构成．

2 运动学分析

2.1 自由度分析

图7中，为便于列写运动旋量，分别在类Exechon并联机构模块的动、静平台几何中心和点处设置相应的连体坐标系和，其中，坐标轴轴沿着2方向，轴垂直于静平台；轴沿着2方向，轴垂直于动平台；其余轴线方向由右手定则确定. 此外，在点处设置动平台的参考坐标系'''，并令坐标轴'、'和'分别平行于坐标轴、和．

如图7所示，类Exechon并联机构模块中沿各个关节转轴方向的单位方向向量同时满足以下几何约束条件：

 (1)

以下对图7所示的类Exechon并联机构模块展开运动学分析．在任意机构位姿下，运动支链1的运动螺旋系为

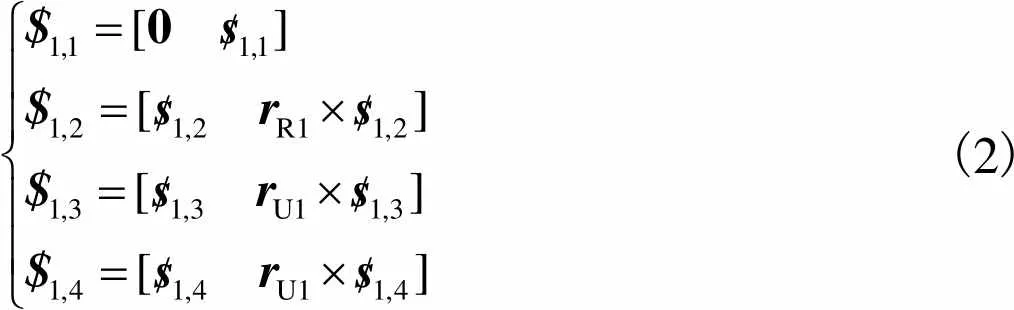
 (2)

对式(2)进行反螺旋运算，即可得到运动支链1的约束螺旋系

 (3)

类似地，可给出运动支链2和3的运动螺旋系，并由反螺旋运算分别求得相应支链的约束螺旋系为

 (4)

 (5)

组合式(3)~(5)所示的运动支链约束螺旋系，即为类Exechon并联机构模块动平台的约束螺旋系

 (6)

对式（6）进行反螺旋运算，即为类Exechon并联机构模块动平台的运动螺旋系

 (7)

2.2 奇异性分析

并联机构动平台的运动输出是其所连接的各个支链的运动叠加．对类Exechon并联机构模块而言，其动平台在参考坐标系'''下的运动螺旋可以表示为

    i＝1，2，3(8)

  i＝1，3(9)

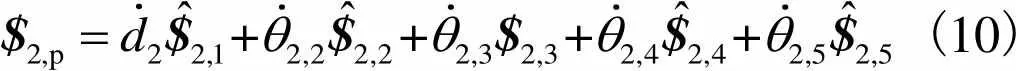
 (10)

在此参考坐标系下，运动支链1和3的运动螺旋系可以表示为

    i＝1，3(11)

对式(11)进行反螺旋运算，即可得到运动支链1和3的约束螺旋系

    i＝1，3(12)

同理，可在参考坐标系下列写运动支链2的运动螺旋系，并由反螺旋运算求得其约束螺旋系

 (13)

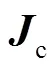
 (14)

 (15)

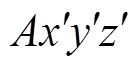
 (16)

 (17)

 (18)

 (19)

 (20)

2.3 逆运动学分析

根据类Exechon并联机构模块的结构特点，可构建其逆运动学模型，如图8所示．

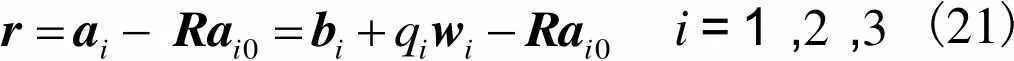
  i＝1，2，3(21)

    (22)

图8 类Exechon并联机构模块的逆运动学模型

 (23)

计入式(1)所示的类Exechon并联机构模块各个关节转轴的几何约束条件，并将式(23)带入式(21)所示的矢量闭环方程，即可求解类Exechon并联机构模块连带运动方程.选定、和为动平台的独立运动参数，可分别得到Exechon、Exe-Variant、Exe-Ⅰ和-Ⅱ并联机构的连带运动方程，即

 (24)

 (25)

 (26) (27)

将以上连带运动方程回代到式(21)的闭环矢量方程，可得到该类并联机构运动学逆解的统一表达形式为

  i＝1，2，3(28)

据此，可求得类Exechon并联机构模块动平台上操作头末端的位置矢量

 (29)

2.4 工作空间分析

开展并联机构工作空间分析时，其腿长范围、转角极限、支链干涉等主要约束条件可描述如下。

(1)对于并联机构模块中运动支链的腿长约束，支链满足如下约束条件：

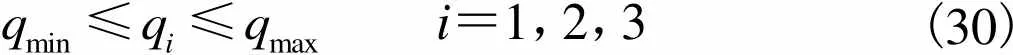
   i＝1，2，3(30)

式中min和max分别为运动支链最小和最大腿长.

(2)对于并联机构模块中支链(＝1，2，3)上关节的转角约束，R、U和S副可分别被等效为个交叉的转动关节，并满足如下约束条件．

转动副(R：＝1)的转角为

 (31)

式中R为机构中转动副的极限转角．

虎克铰(U；＝1，2)的转角为

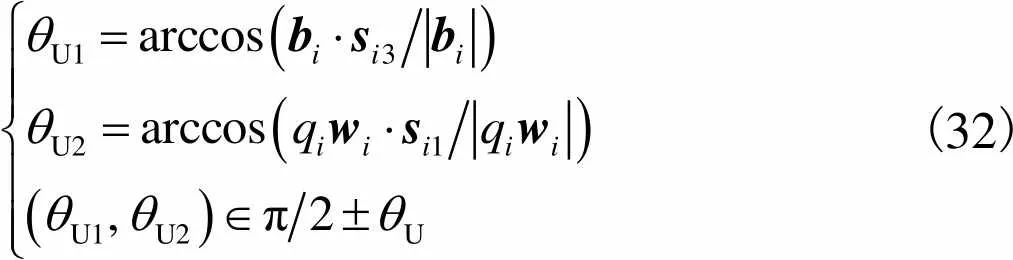
 (32)

式中U为机构中虎克铰的极限转角．

球铰(S：＝1，2，3)的转角为

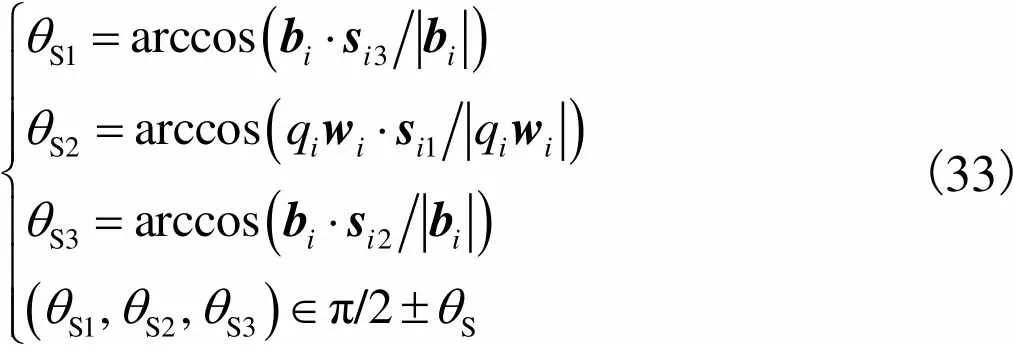
 (33)

式中S为机构中球铰的极限转角．

(3)对于并联机构模块中运动支链和支链＋1之间不发生干涉的约束条件[30]为

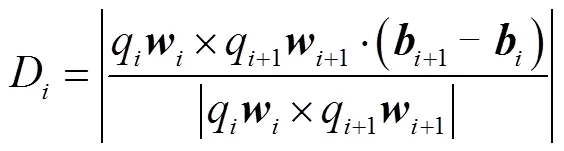
     i＝1，2，3(34)

式中D和分别为相邻支链间的最短公法线长度和支链最大宽度．

以图4的样机设计为例，预估类Exechon并联机构模块的动平台可达工作空间，其几何参数可由相应的虚拟样机模型测得，具体如表2所示．

表2 并联机构的几何参数

Tab.2 Geometricparameters of the proposed PKMs

在以上运动学逆解分析的基础上，运用笔者前期针对类Exechon并联机构设计的“分层切片”式工作空间搜索方法[7]，可预估得到同一机构尺寸条件下，前述4种类Exechon并联机构模块的动平台可达工作空间，分别如图9(a)~(d)所示．

分析图9可知，4种类Exechon并联机构的动平台可达工作空间形状及大小均与构型密切相关，并关于＝0对称分布，这与并联机构中支链1、3关于支链2对称布置相对应．为直观对比，不妨以工作空间包络体积的大小来衡量该类并联机构的工作空间性能.经分析，4种类Exechon并联机构的工作空间包络体积分别是0.317m·rad2、0.445m·rad2、0.477m·rad2和0.538m·rad2，亦即同一机构尺寸条件下，新设计的Exe-Ⅰ并联机构和Exe-Ⅱ并联机构可达工作空间性能优于原Exechon并联机构和Exe-Variant并联机构．

2.5 运动学性能对比

通过以上运动学建模与分析不难发现：针对类Exechon并联机构的可重构设计，在保留部分运动学特性的同时也显著影响了另一部分，具体见表3．

由表3可知，文中基于可重构概念设计的类Exechon并联机构模块都保留了与Exechon并联机构相同的自由度和结构奇异性．此外，相比于其他几种类Exechon并联机构，Exe-Ⅰ并联机构拥有更加简单的牵连运动，便于运动学控制；而Exe-Ⅱ并联机构拥有更大的工作空间，可以实现更大的加工范围；亦即可重构设计显著改善了部分类Exechon并联机构的逆运动学连带运动的复杂程度以及动平台可达工作空间的分布．

表3 并联机构的运动学性能对比

Tab.3 Kinematiccomparisons of the PKMs

图9 类Exechon并联机构的可达工作空间

3 实 验

3.1 实验样机

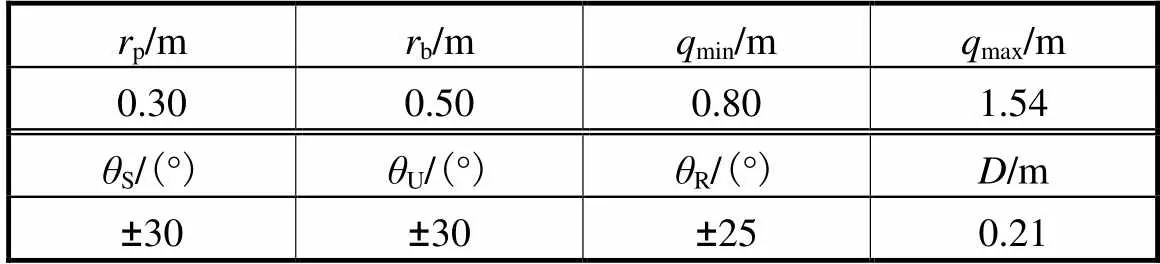
借助3D打印技术，制作了类Exechon型Exe-Ⅰ并联机构模块的原理样机，如图10所示．图10中，Exe-Ⅰ并联机构模块的拓扑结构及运动副设置参见图6(a)所示的概念设计，其主要几何参数如表4  所示．

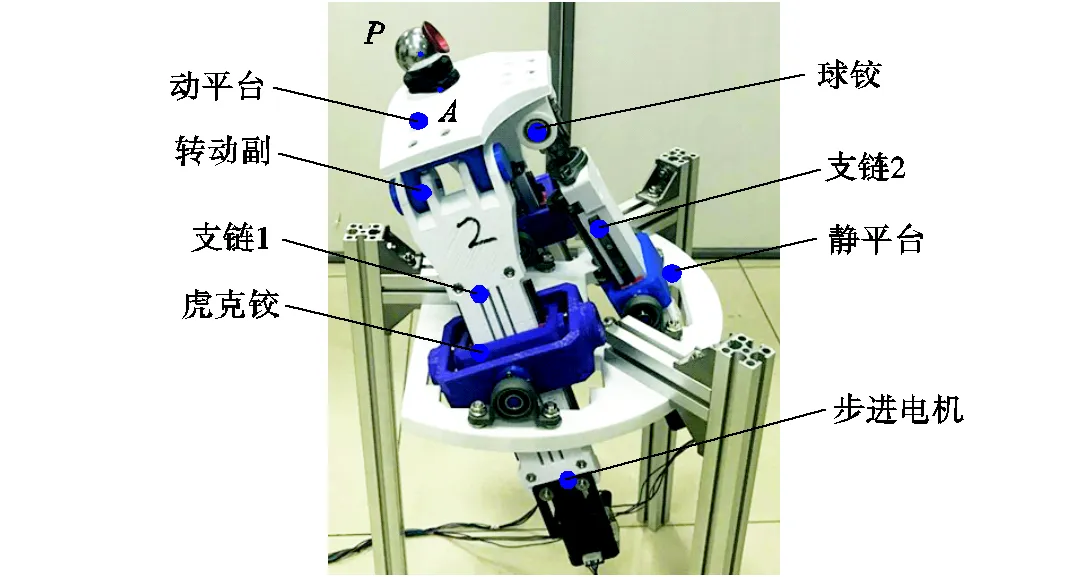
图10 Exe-Ⅰ并联机构模块原理样机

表4 Exe-Ⅰ并联机构原理样机的几何参数

Tab.4 Geometricparameters of the Exe-Ⅰ PKM

3.2 实验方案

以图10中给出的类Exechon型Exe-Ⅰ并联机构模块的原理样机为例，开展如图11所示的运动精度实验，用以验证前文提出的类Exechon并联机构模块的运动学模型．

如图11所示，上位机（PC）将期望位姿的点位数据传输给下位机(基于DSP的控制模块)，进而通过与DSP模块通讯的电机驱动器驱动对应支链的步进电机，实现动平台末端点预定的轨迹输出. 与此同时，激光追踪仪(LEICA AT960)实时追踪位于动平台末端的标定球(点)，并通过与之相连的数采计算机记录动平台末端的轨迹数据．

3.3 实测结果与分析

为充分验证Exe-Ⅰ并联机构模块的2R1T运动能力，设置其动平台末端点的期望轨迹为一空间螺旋线．采用如图11所示的运动精度实验设计进行实验，并测量位于末端点的运动轨迹上的n个(＝1，2，…，33)离散点，其结果如图12所示．

由图12可知，实验所得的末端点的运动轨迹构成一空间螺旋线，并与相应的理论分析轨迹吻合较好．这一现象表明：类Exechon型Exe-Ⅰ并联机构模块能够实现2个转动自由度和1个移动自由度的2R1T运动能力，验证了第2.1节中有关类Exechon并联机构模块的自由度分析结论．

为直观地分析Exe-Ⅰ并联机构模块的运动精度，以末端点的3个坐标分量为分析对象，给出螺旋运动轨迹的运动精度对比，如图13所示．

图11 类Exechon并联机构模块的运动精度实验

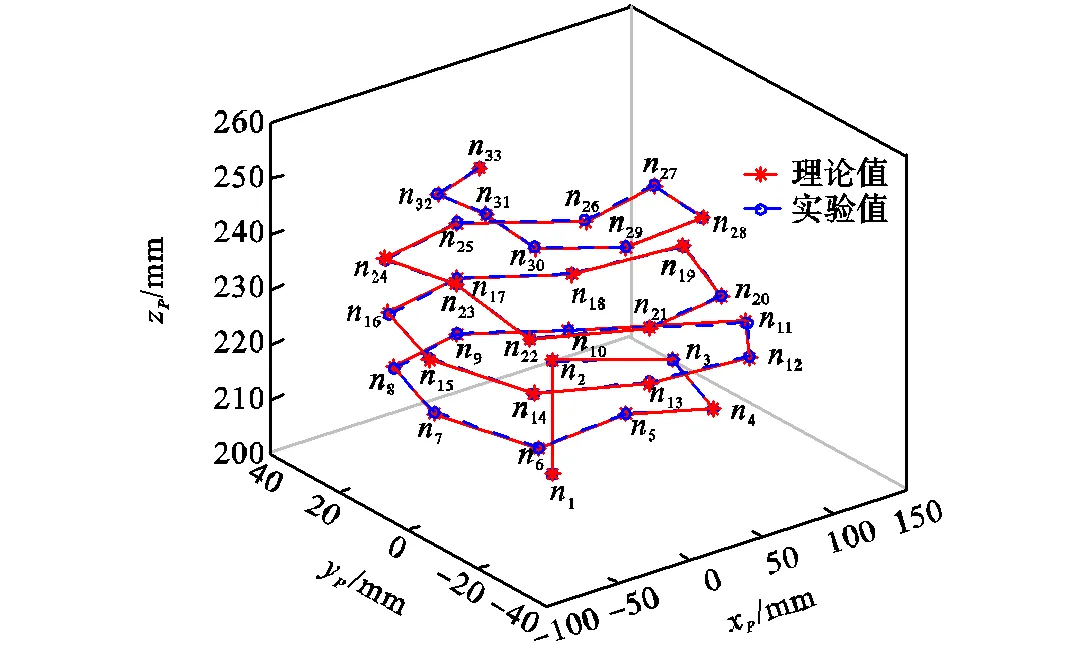
图12 Exe-Ⅰ并联机构模块的实验测试轨迹

如图13所示，Exe-Ⅰ并联机构模块末端点的各个坐标分量的实验值和理论值都吻合较好，数据的绝对误差在±0.4mm以内，并且其相对误差不大于实验值的3.2%，验证了前文中类Exechon并联机构模块的运动学逆解模型的有效性及Exe-Ⅰ并联机构模块实验样机的设计精度．

图13 Exe-Ⅰ并联机构模块的运动精度对比

由于作为实验对象的并联机构原理样机是采用熔融沉积式的3D打印技术制作，推测以上实验误差来源于打印材料的结构塑性和运动关节的装配间隙.因此，有望通过采用塑性变形较小的打印材料、在运动学中计及关节间隙或对并联机构进行实时运动补偿，搭建更高精度的类Exechon并联机构模块.此部分内容，将另行撰文讨论.

4 结 论

(1)提出了基于两类可锁定球关节和模块化运动支链的可重构并联机构模块概念设计，给出了可锁定球关节的变换过程以及关节转轴的设置方案，完成了4种类Exechon并联机构模块的可重构设计．

(2)运动学分析表明：4种类Exechon并联机构模块均具有2R1T运动能力；在一定条件下存在结构奇异位姿，但始终不存在约束奇异；同一机构尺寸条件下，Exe-Ⅰ和Exe-Ⅱ并联机构可达工作空间性能优于Exechon和Exe-Variant并联机构．

(3)通过可锁定关节设计，在模块化运动支链层面开展的机构可重构设计，保留了与Exechon并联机构相同的自由度和结构奇异性，并显著改善了部分类Exechon并联机构的逆运动学连带运动的复杂程度以及动平台可达工作空间的分布．

(4)借助3D打印技术制作了一型并联机构原理样机，并通过运动精度实验验证了运动学分析的正确性．本文所开展的可重构概念设计和运动学分析，为类Exechon并联机构模块的工程样机设计、加工柔性设计和模块化工程应用打下了良好基础．

［1］ Chen Xiang，Liu Xinjun，Xie Fugui，et al. A comparison study on motion/force transmissibility of two typical 3-DoF parallel manipulators: The sprint Z3 and A3 tool heads[J]. International Journal of Advanced Robotic Systems，2014，11(1)：1-10.

［2］ 赵 庆，王攀峰，黄 田. 考虑链间耦合的高速并联机器人惯性参数预估方法[J]. 天津大学学报：自然科学与工程技术版，2017，50(8)：868-876.

Zhao Qing，Wang Panfeng，Huang Tian. An inertial parameter estimation method for high-speed parallel robots by considering inter-chain coupling[J]. Journal of Tianjin University：Science and Technology，2017，50(8)：868-876(in Chinese).

［3］ 刘海涛，熊 坤，贾昕胤，等. 3自由度冗余驱动下肢康复并联机构的运动学优化设计[J]. 天津大学学报：自然科学与工程技术版，2018，51(4)：357-366.

Liu Haitao，Xiong Kun，Jia Xinyin，et al. Kinematic optimization of a redundantly actuated 3-DOF parallel mechanism for lower-limb rehabilitation[J]. Journal of Tianjin University：Science and Technology，2018，51(4)：357-366(in Chinese).

［4］ Bi Z M，Jin Yan. Kinematic modeling of Exechon parallel kinematic machine[J]. Robotics and Computer Integrated Manufacturing，2011，27(1)：186-193.

［5］ 张 俊，赵艳芹. Exechon并联模块的静刚度建模与分析[J]. 机械工程学报，2016，52(19)：34-41. Zhang Jun，Zhao Yanqin. Stiffness modeling and evaluation for Exechon parallel kinematic machine module[J]. Journal of Mechanical Engineering，2016，52(19)：34-41(in Chinese).

［6］ Jin Yan，Mctoal P，Higgins C，et al. Parallel kinematic assisted automated aircraft assembly[J]. International Journal of Robotics and Mechatronics，2014，1(3)：89-95.

［7］ Tang Tengfei，Zhao Yanqin，Zhang Jun，et al. Conceptual Design and Workspace Analysis of an Exechon-Inspired Parallel Kinematic Machine[M]// Advances in Reconfigurable Mechanisms and Robots II. Cham，Switzerland：Springer Publishing Company，2016：445-453.

［8］ Jin Yan，Bi Z M，Liu Haitao，et al. Kinematic analysis and dimensional synthesis of exechon parallel kinematic machine for large volume machining[J]. ASME Journal of Mechanisms and Robotics，2015，7(4)：041004-01-041004-8.

［9］ Jin Yan，Bi Z M，Higgins C，et al. Optimal design of a new parallel kinematic machine for large volume machin-ing[M]//Advances in Reconfigurable Mechanisms and Robots I. London，UK：Springer Publishing Company，2012：343-354.

［10］Zlatanov D，Zoppi M，Molfino R. Constraint and singularity analysis of the Exechon tripod[C]// ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. USA：ASME，2012：679-688.

［11］柴馨雪，项济南，李秦川. 2-UPR-RPU 并联机构奇异分析[J]. 机械工程学报，2015，51(13)：144-151. Chai Xinxue，Xiang Jinan，Li Qinchuan. Singularity analysis of a 2-UPR-RPU parallel mechanism[J]. Journal of Mechanical Engineering，2015，51(13)：144-151(in Chinese).

［12］Jin Yan，Lian Binbin，Price M，et al. QrPara：A new reconfigurable parallel manipulator with 5 axis capability[M]//Advances in Reconfigurable Mechanisms and RobotsⅡ. Cham，Switzerland：Springer Publishing Company，2016：247-258.

［13］Zhang Jun，Zhao Yanqin，Jin Y. Kinetostatic model based stiffness analysis of Exechon PKM[J]. Robotics and Computer Integrated Manufacturing，2016，37：208-220.

［14］Bi Z M. Kinetostatic modeling of Exechon parallel kinematic machine for stiffness analysis[J]. The International Journal of Advanced Manufacturing Technology，2014，71(1/2/3/4)：325-335.

［15］Bonnemains T，Chanal H，Bouzgarrou B C，et al. Dynamic model of an overconstrained PKM with compliances：The Tripteor X7[J]. Robotics and Computer Integrated Manufacturing，2013，29(1)：180-191.

［16］Zhang Jun，Zhao Yanqin，Jin Yan. Elastodynamic modeling and analysis for an Exechon parallel kinematic machine[J]. ASME Journal of Manufacturing Science and Engineering，2016，138(3)：031011-1-031011-14.

［17］Bi Z M，Lang S Y T，Verner M，et al. Development of reconfigurable machines[J]. The International Journal of Advanced Manufacturing Technology，2008，39(11/12)：1227-1251.

［18］黄 田，李 曚，吴孟丽，等. 可重构PKM模块的选型原则——理论与实践[J]. 机械工程学报，2005，41(8)：36-41.

Huang Tian，Li Meng，Wu Mengli，et al. Criteria for conceptual design of reconfigurable PKM modules—theory and application[J]. Journal of Mechanical Engineering，2005，41(8)：36-41(in Chinese).

［19］Song Chaoyang，Feng Huijuan，Chen Yan，et al. Reconfigurable mechanism generated from the network of Bennett linkages[J]. Mechanism and Machine Theory，2015，88：49-62.

［20］Zhang Ketao，Dai Jian S，Fang Yuefa. Geometric constraint and mobility variation of two 3SvPSv metamorphic parallel mechanisms[J]. ASME Journal of Mechanical Design，2013，135(1)：011001-1-011001-8.

［21］Gan Dongming，Dai Jian S，Dias J，et al. Unified kinematics and singularity analysis of a metamorphic parallel mechanism with bifurcated motion[J]. ASME Journal of Mechanisms and Robotics，2013，5(3)：031004-1-031004-11.

［22］Gan Dongming，Dias J，Seneviratne L. Unified kinematics and optimal design of a 3rRPS metamorphic parallel mechanism with a reconfigurable revolute joint[J]. Mechanism and Machine Theory，2016，96：239-254.

［23］Gan Dongming，Dai Jian S，Dias J，et al. Variable motion/force transmissibility of a metamorphic parallel mechanism with reconfigurable 3T and 3R motion[J]. ASME Journal of Mechanisms and Robotics，2016，8(5)：051001-1-051001-9.

［24］Kong Xianwen，Jin Yan. Type synthesis of 3-DOF multi-mode translational/spherical parallel mechanisms with lockable joints[J]. Mechanism and Machine Theory，2016，96：323-333.

［25］Palpacelli M C，Carbonari L，Palmieri G，et al. Analysis and design of a reconfigurable 3-DoF parallel manipulator for multimodal tasks[J]. IEEE/ASME Transactions on Mechatronics，2015，20(4)：1975-1985.

［26］Carbonari L，Callegari M，Palmieri G，et al. A new class of reconfigurable parallel kinematic machines[J]. Mechanism and Machine Theory，2014，79：173-183.

［27］Kong Xianwen，Huang Chintien. Type synthesis of single-DOF single-loop mechanisms with two operation modes[C]// International Conference on Reconfigurable Mechanisms and Robots. London，UK，2009：136-141.

［28］叶 伟，方跃法，郭 盛，等. 基于运动限定机构的可重构并联机构设计[J]. 机械工程学报，2015，51(13)：137-143.

Ye Wei，Fang Yuefa，Guo Sheng，et al. Design of reconfigurable parallel mechanisms with discontinuously movable mechanism[J]. Journal of Mechanical Engineering，2015，51(13)：137-143(in Chinese).

［29］Tang Tengfei，Zhang Jun. Conceptual design and comparative stiffness analysis of an Exechon-like parallel kinematic machine with lockable spherical joints[J]. International Journal of Advanced Robotic Systems，2017，14(4)：1-13.

［30］黄 真，赵永生，赵铁石. 高等空间机构学[M]. 北京：高等教育出版社，2006.

Huang Zhen，Zhao Yongsheng，Zhao Tieshi. Advanced spatial Mechanism[M]. Beijing：Higher Education Press，2006(in Chinese).

Conceptual Reconfigurable Design and Kinematic Analysis of the Exechon-Like Parallel Kinematic Machine

Tang Tengfei，Fang Hanliang，Zhang Jun

(School of Mechanical Engineering and Automation，Fuzhou University，Fuzhou 350116，China)

Reconfigurable and modular designs can be a key technology to realize the versatility as well as improve the flexibility of parallel kinematic machines(PKMs). Inspired by the design of the high-performance Exechon PKM，two novel Exechon-like PKMs—Exe-Ⅰ and Exe-Ⅱ are proposed on the basis of the Exe-Variant PKM. Four types of reconfigurable Exechon-like PKM modules—Exechon，Exe-Variant，Exe-Ⅰ，and Exe-Ⅱ were conceptually designed by following the design flows of lockable joints，modular limbs，and reconfigurable PKMs. With regard to the kinematic analysis of Exechon-like PKMs，the degrees of freedom(DoF)and singularities were analyzed with the screw theory，wherein the screw systems of the Exechon-like PKMs were formulated and overfull Jacobian matrices of the PKMs were derived. Loop-closure equations were formulated to develop the inverse kinematic model and parasitic motions of the moving platform. The reachable workspaces of the proposed PKMs were predicted by a “sliced partition” algorithm. A comparative analysis of the kinematics shows that the reconfigurable design of the Exechon-like PKMs can keep the DoF of the PKMs and their architectural singularities unchanged. The analysis also shows that the reconfigurable design can significantly improve the complexity of the parasitic motions of inverse kinematics and the distributions of the moving platform’s reachable workspaces for several Exechon-like PKMs. Finally，using the 3D printing technology，a laboratory prototype of Exe-Ⅰ PKM was built to conduct the kinematic experiment. The experimental values agree well with the theoretical values. The absolute error is less than ±0.4 mm and the relative error is within 3.2%，which verifies the effectiveness of the proposed kinematic analysis module. The conceptual designs of reconfigurable and modular PKMs in this study can prove to be key techniques to realize efficient reconfigurable designs and engineering applications of Exechon-like PKMs.

parallel kinematic machine；lockable joint；reconfigurable；kinematics

10.11784/tdxbz201808073

TH112

A

0493-2137(2019)07-0733-12

2018-08-25；

2018-11-08.

汤腾飞（1991—  ），男，博士研究生，tengfei413zm@163.com.

张 俊，zhang_jun@fzu.edu.cn.

福建省工业机器人基础部件技术重大研发平台资助项目(2014H2004).

the Fujian Provincial Industrial Robot Basic Components Technology Research and Development Center(No. 2014H2004).

(责任编辑：金顺爱)