负磁致伸缩材料对电机振动噪声抑制的分析

张 欣，姚 娜，李 璞

(天津工业大学，天津 300387)

0 引 言

电机广泛存在于人类生活中，尤其在石油、化工等重工业领域中占有非常重要的位置。一些军工企业对电机噪声要求更高[1]，因此电机振动噪声的抑制是非常重要的。电机的电磁噪声主要来源是电磁力和磁致伸缩力共同作用而造成的[2]，电磁力在宏观上可以分为麦克斯韦力和安培力，麦克斯韦力存在于转子和定子间的空隙中，由气隙磁场、槽谐波等因素产生的随时间和空间变化的力；安培力是电枢电流在磁场作用下而产生的力，也就是微观上运动电荷在磁场作用下受到的洛伦磁力。磁致伸缩是在外加磁场下磁致伸缩材料沿着磁场方向产生伸长和缩短，负磁致伸缩是指铁磁材料沿磁场方向尺寸变小[3-4]，Ni 和SmFe2是具有负磁致伸缩特性的材料[5]。

文献[6-7]表明，当电机在高强度磁场下即磁密高于1.5 T或激励源含有高次谐波时，定子硅钢片由于其磁致伸缩的作用，产生的力可占总电磁力的一半。近年来，在计算电机振动噪声时都考虑了电机定子硅钢片的磁致伸缩效应，且以不同的模态进行了分析[8-9]，但仅研究了磁致伸缩效应对电机电磁噪声的影响以及大小，对于如何减小其引起的振动噪声，国内外还处于探索阶段。英国学者 Sakda Somkun 与其团队对无取向电工钢的磁致伸缩各向异性进行了研究，对感应电动机的定子齿进行了变形测量,并与实测变形进行了比较，研究结果表明，磁致伸缩各向异性会造成电机定子齿发生明显的不对称变形[10]。日本学者Enokizono介绍了机械应力对无取向电工钢二维磁致伸缩和矢量磁性的影响，并开发了六轴应变仪，用来测量无取向电工钢的面内机械应力和磁致伸缩，同时还测量了在拉伸和压缩应力下的矢量磁性和二维磁致伸缩，根据测量结果，获得了由于施加机械应力引起的矢量磁性和二维磁致伸缩的差异[11]。沈阳工业大学韩雪岩教授及其团队以不同频率的永磁电机为例，分别计算了磁致伸缩力和电磁力以及两者共同作用时电机振动情况，并计算在这两种力下电机周围空气噪声的大小，通过实验验证，得到磁致伸缩力对电机振动噪声有一定的影响，在计算电机噪声时不能忽略电机定子铁心的磁致伸缩效应[12-13]。

本文首先建立了电磁-机械的耦合模型，在有限元中计算并分析了由磁致伸缩效应引起的定子结构的振动，并进行了电机定子硅钢片上打孔以及填充负磁致伸缩材料的仿真计算。

1 电磁-机械耦合数值模型

本文选用多物理场耦合分析软件COMSOL Multiphysics进行电机定子硅钢片的建模与应力计算，在计算电机定子硅钢片的振动时，选用软件的固体力学模块来分析，其求解方程：

T-Ti=C(S-Si) (2)

式中:ρ是密度；T是所受应力；Ti是初始应力设定值；C是刚度矩阵；S是应变；Si是初始应变值；u是位移矢量；F是载荷量；ν是泊松比。

电机定子硅钢片的磁致伸缩本构关系是基于线性压磁方程表示的，其方程：

εH=σ/Eσ+dH(3)

Bσ=μσH+dσ(4)

式中：εH是应变；Eσ为杨氏模量；σ为应力；d是磁致伸缩系数；H为磁场强度；Bσ是应力作用下的磁感应强度；μσ是应力作用下的磁导率。

本文利用弹性力学这一原理来计算无取向硅钢片的磁致伸缩力。根据弹性力学基本原理，其应力与应变的本构关系可以用一个线性方程式来表示，硅钢片内部的振动只有平面方向，而在高度方向没有变化，即这一方向值是不变的。则无取向硅钢片内任一点应力与应变的关系可表示：

σ=Dξ(5)

式中:σ为磁致伸缩应力；D为弹性张量；ξ为磁致伸缩应变。对于线性二维弹性材料，弹性张量D由矩阵表示:

(6)

式中:E是弹性材料的杨氏模量；α为弹性材料的泊松比。

整个电磁-机械数值模型耦合的过程可由耦合方程表示：

SA=Je(7)

KU=F(8)

式中:S是电磁刚度矩阵；A是磁场矢量；U是振动位移矩阵；Je是外部电流密度；K是机械刚度矩阵；F是作用力。

本文先在电磁-机械场计算电机定子硅钢片的磁场，再将磁场与固体力学两者进行耦合，得到磁致伸缩应变与应力，从而得到电机定子硅钢片的振动。

2 数值计算

本文以三相交流电机为例，根据上述数值模型对电机定子硅钢片进行有限元分析，电机的主要参数如表1 所示。

表1 电机主要参数

在有限元仿真软件COMSOLMultiphysics中设置通入电机绕组的电流为三相交流电，电流幅值为2A,频率为80Hz，此时电机绕组产生旋转磁场。

图1为在磁致伸缩力作用下电机定子硅钢片的应力分布及受应力而产生的形变图。观察图1可知，其应力分布每处都不相同，但在电机定子齿根和齿尖处应力较大，硅钢片在沿着磁场方向发生了伸长的形变，则电机定子硅钢片在外加磁场作用下有磁致伸缩且为正磁致伸缩力。

图1电机定子应力及形变图

选取电机定子应力变化较大的齿根和齿尖处一点进行应力分析，如图2所示，点1位于定子齿根处，点2位于定子齿尖处。这两点的振动响应如图3所示，应力呈正弦变化，定子齿根处应力模值小于定子齿尖处应力模值。

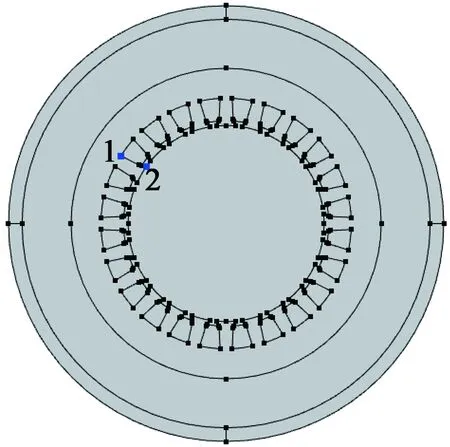
图2应力分析点的选取

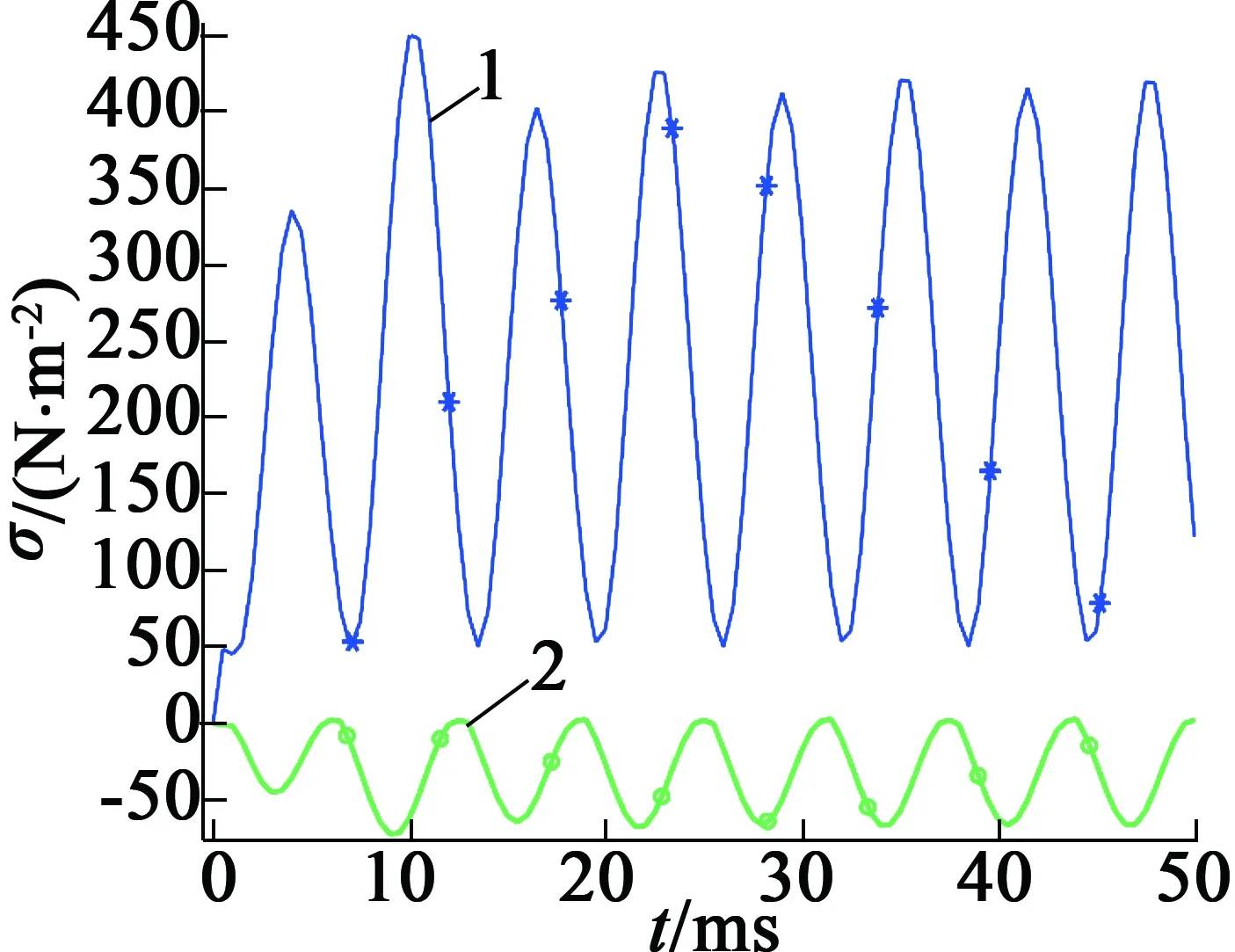
图3电机定子齿根和齿尖应力时变图

3 硅钢片上打孔并填充负磁致伸缩材料

由图1可知，电机定子硅钢片是具有正磁致伸缩效应的，而负磁致伸缩材料与硅钢片的磁致伸缩性能是相反的，这样就使得彼此产生的形变抵消，降低电机振动噪声。本文选用了两种具有不同负磁致伸缩特性的材料Ni和SmFe2来进行填充，主要参数如表2所示。

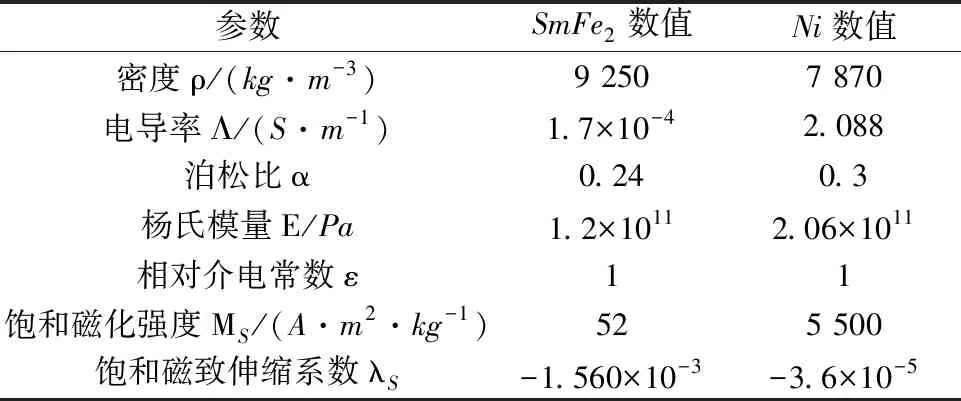
表2 Ni和SmFe2材料参数

由图1可以看到，应力集中在电机定子齿和齿根处，且由图3可知，在定子齿根处其振动较大，所以选取在接近定子齿根处打孔，孔为直径3mm的圆，如图4所示。

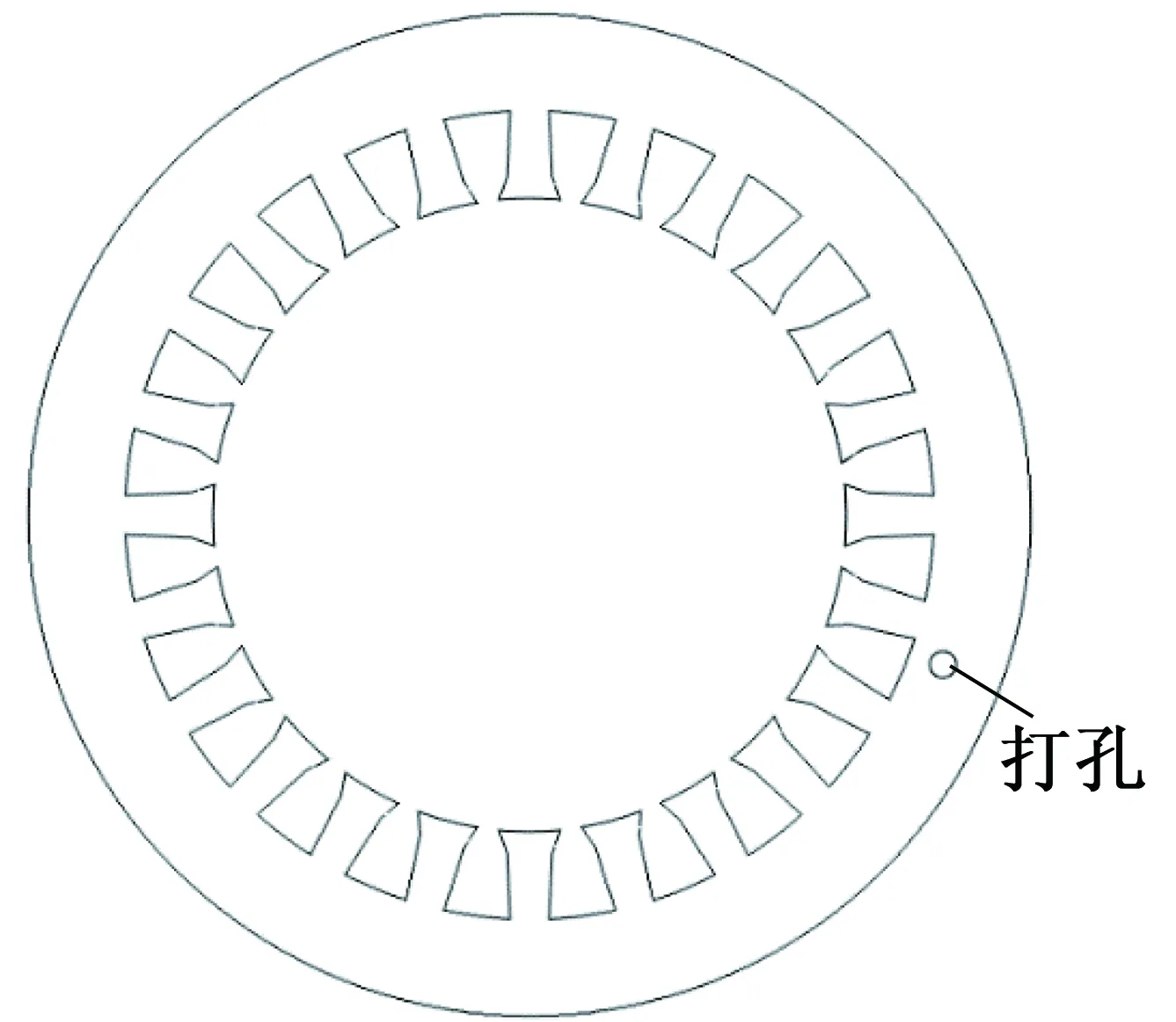
图4电机定子打孔位置

在打孔处分别填充负磁致伸缩材料Ni和SmFe2，得到其在t=0.2s时的应力，如图5、图6所示。观察其局部应力，较图1应力明显发生了变化。

图5填充Ni的电机定子应力图

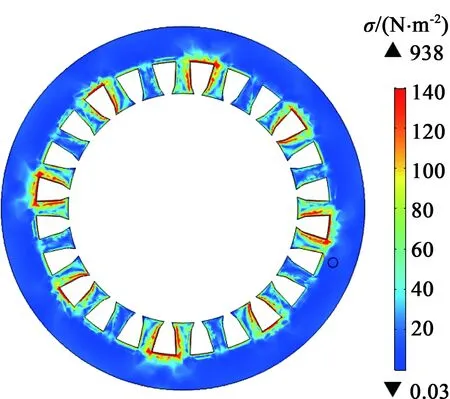
图6填充SmFe2电机定子应力图

在这三种情况定子所受应力最大值和最小值如表3所示。

表3 电机定子硅钢片应力分析

由表3可知，在填充了负磁致伸缩材料Ni和SmFe2之后，电机定子硅钢片所受的最大和最小应力值都变小了，相较于未打孔填充材料，其最大和最小应力值都发生了数量级的变化，且填充不同负磁致伸缩材料其应力变化也不同，填充SmFe2使得电机定子硅钢片所受最小应力是填充Ni的1/2,最大应力值与填充Ni变化不大，主要原因是材料的磁致伸缩特性和杨氏模量不同造成的。杨氏模量为材料应力与应变之比，SmFe2磁致伸缩特性较大，即应变较大，可抵消较多的硅钢片正磁致伸缩，使得材料所受应力变小；而Ni的磁致伸缩特性较小，应变较小，可抵消的硅钢片正磁致伸缩较小。为了进一步分析填充负磁致伸缩材料是否抑制电机振动噪声，计算了电机的振动特性，电机定子硅钢片表面频域振动如图7所示。

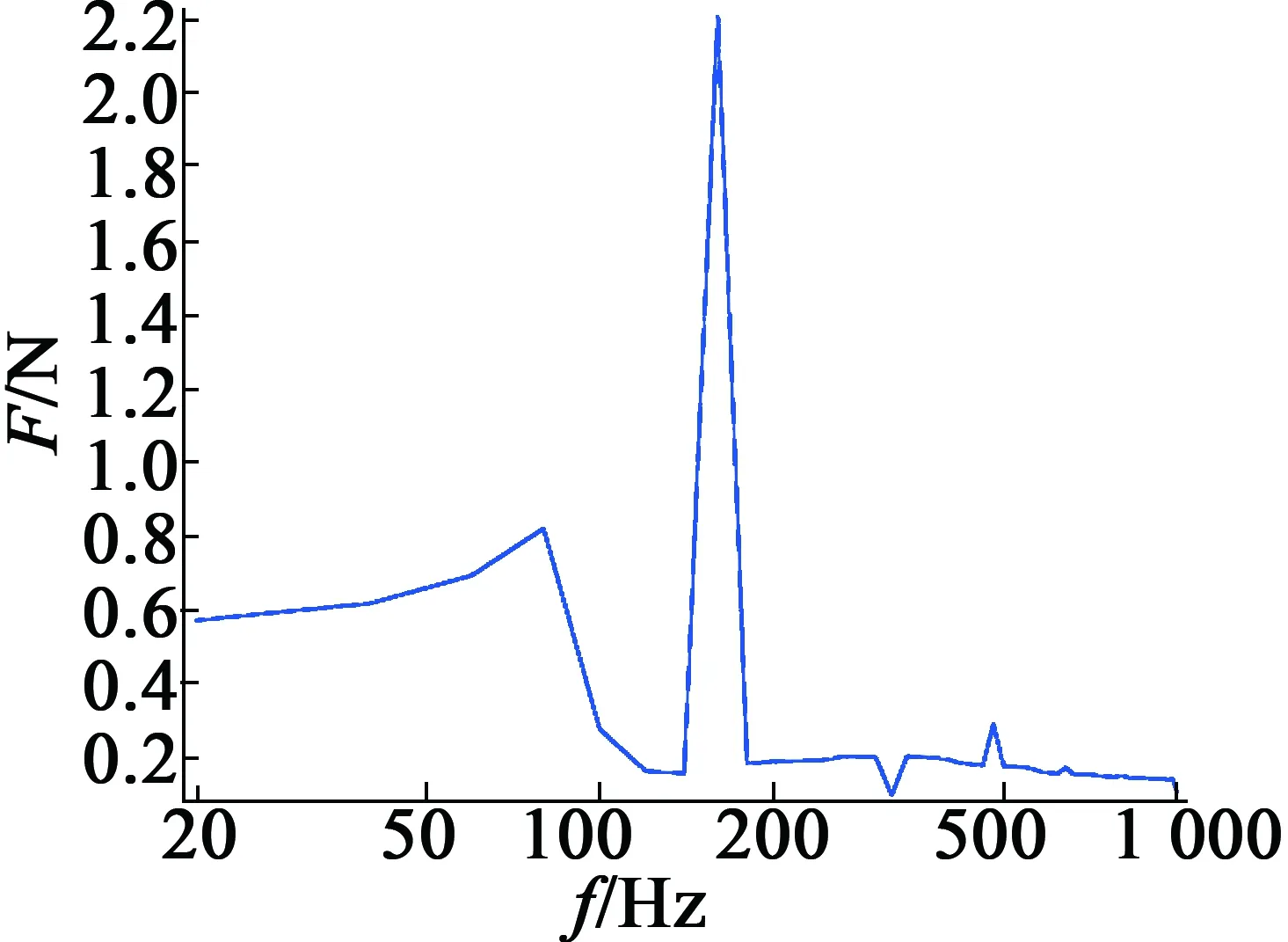
图7电机定子硅钢片表面频域振动

由图7可知，在80Hz(供电频率)处和160Hz(供电频率2倍)处电机定子硅钢片发生了共振，即在这两个频率处振动最大，产生的噪声也更强。由上述分析可知，填充了负磁致伸缩材料之后，电机定子硅钢片的应力值明显发生了变化，对于是否能减少电机的振动噪声，计算了在填充负磁致伸缩材料后电机定子硅钢片的振动情况，如图8所示。

由图8可知，填充负磁致伸缩材料后，在80Hz(供电频率)处和160Hz(供电频率2倍)处的振动较未填充时减小了，主要数值变化如表4所示。可见，填充负磁致伸缩材料可以减小电机振动，从而进一步减小电机电磁噪声。

图8填充负磁致伸缩材料电机定子硅钢片表面频域振动

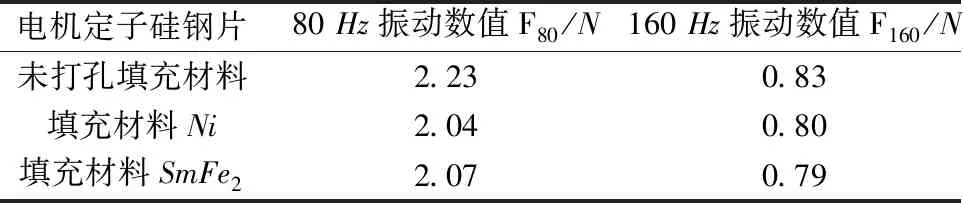
表4 电机定子硅钢片振动分析

同时，分析了在不同频率下，电机定子硅钢片的振动数值如表5所示。在不同频率下，填充负磁致伸缩材料后振动数值也相应减小。因此，在不同供电频率下电机定子硅钢片上填充负磁致伸缩材料可以减小电机振动。

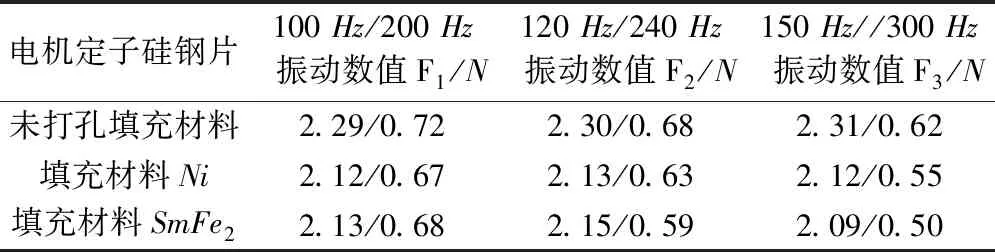
表5 不同频率下电机定子硅钢片振动分析

4 结 语

本文为了研究磁致伸缩效应对电机振动噪声的影响，建立电磁-机械耦合数值模型，用有限元方法计算并分析了由磁致伸缩效应引起的定子硅钢片结构的振动，得到以下结论：电机定子硅钢片在齿根处和齿尖处振动较大；在电机定子硅钢片上打孔并填充负磁致伸缩材料，其电机定子所受应力和明显减小；同时分析了电机定子硅钢片在不同频率下的振动情况，填充负磁致伸缩材料后振动数值也相应减小，从而进一步减小电机振动噪声。但对于孔的位置、大小、数量以及拟填充的负磁致伸缩材料还需进一步优化，才能实现电机振动数值的最小化，进而降低振动噪声。本文为实现电机低噪声运行提供研究方法，具有一定的参考意义。