温度对齿轮齿根应力分布的影响分析

李云奇，张瑞亮，王 铁，王道勇

（太原理工大学齿轮研究所，山西 太原 030024）

1 引言

渐开线齿轮轮齿折断是齿轮失效的主要形式之一[1]，而齿根折断主要是由于齿根应力较大，经疲劳裂纹扩展而导致的。齿轮在工作中齿面会产生相对滑动，摩擦生热会导致其温度升高。所以齿轮在实际工作时，不仅受结构载荷还有温度载荷。齿轮在温度的作用下产生的热应力及热变形会改变齿轮的受力状态和几何特性，进而影响齿轮的工作寿命。故研究温度对齿根应力的影响是十分必要的。

文献[2]通过考虑齿轮啮合过程中的瞬态传热、弹流润滑、表面粗糙度和齿轮材料对第一个接触点进行研究，提出了一种评定热应力和预测热应力引起的接触应力的设计准则的方法。文献[3]通过对比齿轮副在结构场和热弹耦合场的分析结果，主要对齿面上的变形和应力进行研究，并对其进行修形。文献[4]在热-结构耦合中分析了高速重载齿轮的热弹变形，并根据所得到结果及修形理论确定了其齿廓修形曲线。文献[5]通过热弹流计算得到了啮合线上的闪温和最高温度以及他们沿啮合线的分布情况。文献[6]中对螺旋锥齿轮啮合热特性进行分析得到最大热应力出现在齿根位置部位。现有文献就温度对齿面接触应力及热变形等进行了研究，取得了一些有意义的成果，而对温度对齿根应力的影响研究还相对缺乏，因此综合分析热-结构耦合场作用下的齿根应力分布，对齿轮设计和运行具有一定的理论意义和实际应用价值。

首先根据齿轮的工况，对其热边界条件进行计算，通过有限元计算得到其温度场并通过试验进行验证；然后在分析齿轮热应力和热变形的基础上，通过对比齿轮在结构场与热-结构耦合场不同啮合位置时的齿根应力结果，探讨温度对齿轮齿根应力的分布形式及应力最大值的影响。

2 热边界条件计算

2.1 齿轮对流换热系数的计算

2.1.1 齿轮端面对流换热系数计算

式中：ξa—空气的性能参数；ξo—润滑油的性能参数；d—考虑到实际操作条件对混合流动的影响由试验确定的比例因素；αa、αo—空气和润滑油在齿轮端面所占的平均体积比例系数。

采用计算公式如下[7]：

2.1.2 齿轮齿面对流换热系数计算采用计算公式如下[8]：

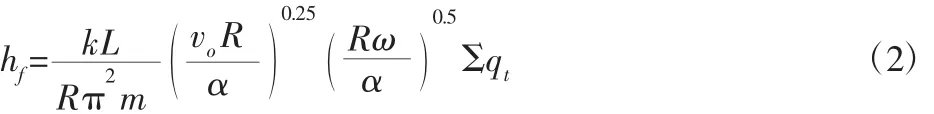
式中：k—润滑油的热传导率；L—齿高；vo—润滑油的运动粘度；α—润滑油的扩散率；Σqt—圆周上新喷入的润滑油的无量纲放热量总和。

式中：ΔTs—齿轮齿面与润滑油温度的差值；β—油液粘度的温度变化系数，近似取 0.03/℃[9]。

2.2 齿面摩擦热流量的计算

齿轮副在任意的啮合位置的接触点C处主从轮的摩擦热流量 q1c、q2c的表达式如下[4]：

式中：下角标1、2—主动轮和从动轮；σ—主从动轮的摩擦热流量分配因子；γ—摩擦能转化成热能的系数，其值一般为（0.9～0.95）；pnc—齿面接触压力；μc—齿面摩擦系数；v—相对滑动速度。

2.3 实例计算

齿轮副传动比为1，主从动齿轮的几何及材料参数完全一致，如表1所示。润滑油采用20号航空润滑油GB440-1977（1988），其在时的理化性能参数[10]，如表2所示。

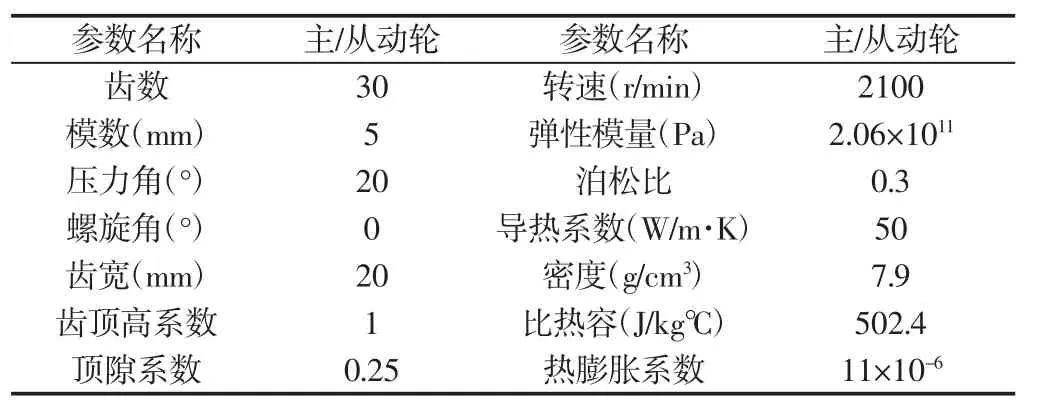
表1 齿轮参数Tab.1 Gear Parameters

表2 润滑油性能参数Tab.2 Lubricant Performance Parameters

根据实际工况取扭矩为1300N·m，为方便加载，端面对流换热系数取其平均值，齿面上的对流换热系数取分度圆位置的值，齿面的摩擦热流量也按平均摩擦热流量计算[11]。计算得到齿根端面平均对流换热系数为155W/m2·k，齿顶端面的平均对流换热系数为193W/m2·k，齿面的对流换热系数为1558W/m2·k，齿面上的平均摩擦热流量为：2.6153×105w/m2。

3 温度对齿轮齿根的影响分析

在三维建模软件中建立齿轮的四齿模型，如图1（a）所示。导入到ANSYS后对进行网格划分，为更好的逼近齿轮曲线的边界，选用20节点的六面体单元进行网格划分，并对目标齿轮齿根过渡曲线段设置为20段进行网格细化。得到网格划分结果，如图1（b）所示。

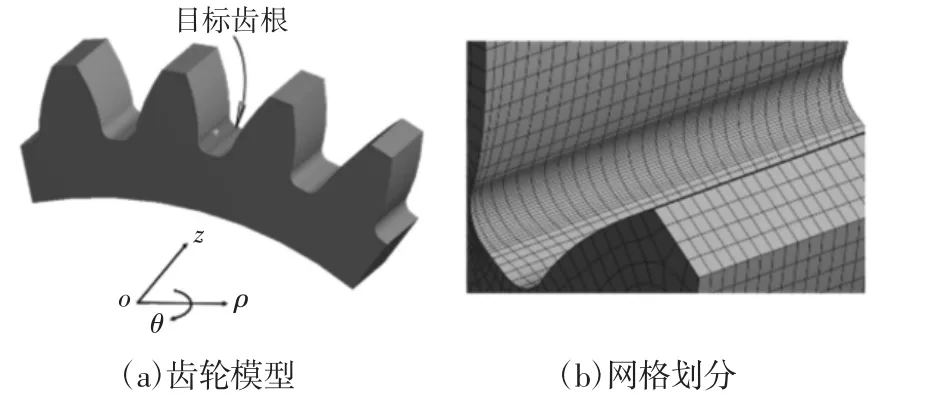
图1 计算模型Fig.1 Computational Model

3.1 齿轮温度场分析

对于齿轮的温度场，为不失一般性采用四齿模型进行分析，如图1（a）所示。齿轮初始温度取实验室室温为23℃，并对齿轮模型的两个周向截面施加周向位移约束，在齿轮的齿面施加齿面对流换热系数，在齿轮的工作齿面施加齿面平均摩擦热流量，在齿轮端面施加齿顶端面对流换热系数和齿根端面对流换热系数。最终的温度场分析结果，如图2所示。由图2可知仿真得出的最低温度为117℃，最高温度为138℃，高温区主要集中在工作面的中心部位，低温区主要是在非工作面的齿根过渡区[11]。为验证计算结果的可信性，在进行齿轮疲劳试验时分别对主试箱的润滑油和轮齿工作齿面的温度进行实时监测，齿轮试验台，如图3所示。

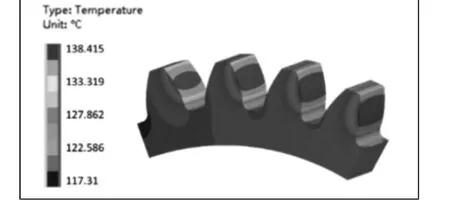
图2 齿轮温度场结果Fig.2 Temperature Field Results of Gear

图3 齿轮试验台Fig.3 Gear Test Stand

首先将温度计和温度传感器同时放入沸水中对温度传感器进行静态标定，在试验过程中通过温度传感器对主试箱中的油液温度进行实时监测，由试验测得主试箱中油液的温度达到稳定时约为为115℃，略低于齿轮的最低温度；在试验停机的瞬间将红外测温仪打到齿轮工作齿面位置测得的齿轮工作齿面的温度为125℃，考虑到停机后齿轮温度会有所降低，可知仿真结果具有一定的可信性。

3.2 齿根热应力分析

在齿轮模型上选取目标齿根后对其进行网格细化进行分析，目标齿根，如图1（a）所示。网格细化，如图1（b）所示。现仅对温度对齿轮齿根应力的影响进行分析，所得目标齿根的热应力分布，如图4所示。

应力云图的上边界为基圆位置，下边界为齿根圆位置，b表示齿宽。由齿根处的热应力可以看出，齿轮齿根在受热载荷的影响下其齿根两侧邻近齿轮端面及齿轮基圆区域的热应力值比较大。经测量后得到热应力最大的位置在距齿轮端面1mm附近。

图4 目标齿根热应力分布Fig.4 Thermal Stress Distribution of Target Tooth Root

3.3 齿根热变形分析

为研究温度对齿根几何特性的影响，对目标齿根的热变形进行分析。首先建立如图1（a）中的坐标系，选取齿轮轴线上一点为原点建立圆柱坐标系，其中，z方向为齿轮轴线方向。在所建立的坐标系中ρ为径向，θ为周向，z为轴向。现通过处理得到目标齿根在此坐标系下各分量的变形情况，如图5所示。

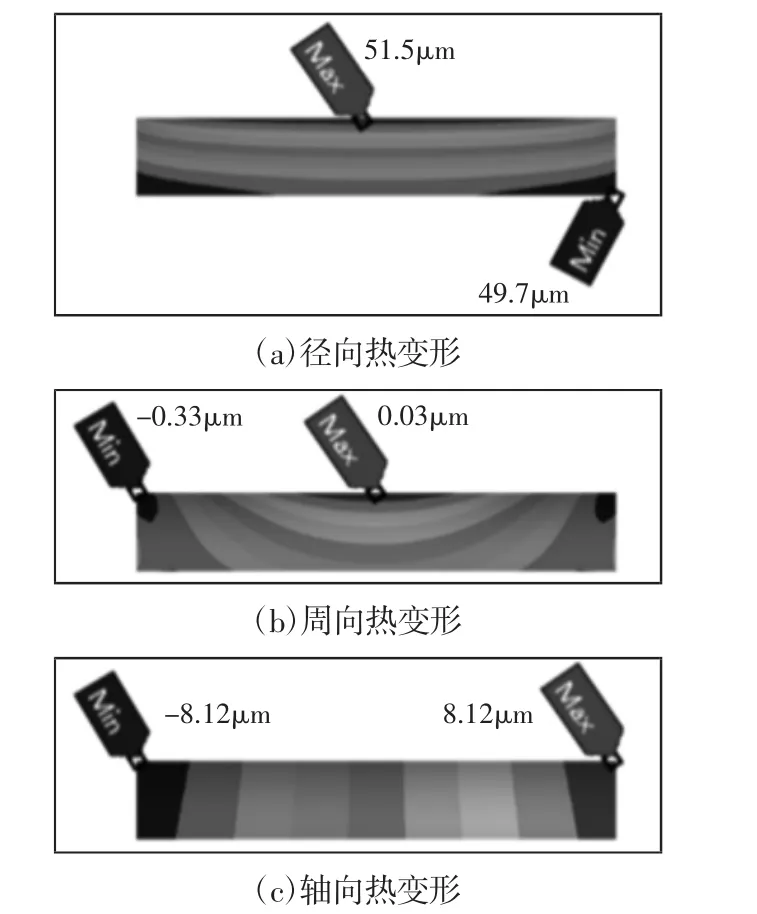
图5 齿根热变形Fig.5 Root Thermal Deformation

由图5（b）可知目标齿根在周向的热变形量很小，可以忽略不计。由图5（c）可知齿根在轴向的热变形呈对称状态分布，即向两端面膨胀约16μm。由图5（a）可知齿根在径向的变形比较明显，且径向热变形由齿根圆处到基圆处呈逐渐增大的趋势，其中，最大值在邻近基圆的中部，为51.5μm；最小值在邻近齿根圆的端面，为49.7μm。为说明径向变形对齿根圆角几何特性的影响，现做齿根径向变形的示意图，如图6所示。

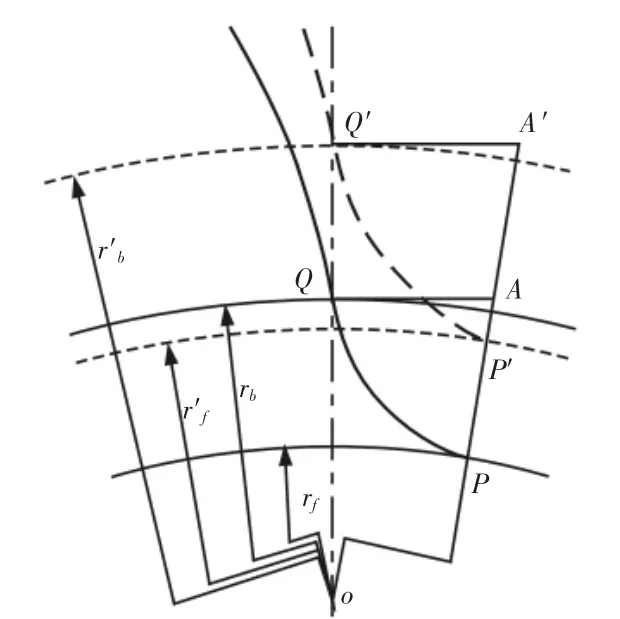
图6 齿根径向热变形示意图Fig.6 Sketch Map of the Radial Thermal Deformation of the Tooth Root

图中：曲线PQ、P′Q′—变形前后的齿根曲线。由于表示的是在径向分量上的变形，故变形前后的齿根曲线与齿根圆和基圆连接位置的几何关系不变，即热变形前后齿根曲线两端的法线方向夹角有：

由图5中的热变形分布可知齿根区在径向有较大的热膨胀变形，且由P到Q逐渐增大，即可以得到变形前后的曲线的弧长关系有：由式（5）、式（6）两式可以得出齿根径向的热变形会使齿根曲线的曲率半径增大。

4 齿根应力有限元对比分析

在前文中通过试验验证了温度场的结果是可信的。下面通过对齿轮副在某个齿上的啮合过程中进行结构场分析以及热-结构耦合场的分析，再将两种状态下的齿根应力状态进行对比，以此来说明温度对齿根应力的影响。

在目标齿根对应的啮合齿面上以齿轮绕基圆圆心转动的角度均等选取选取10个不同的位置进行对比分析，如图7所示。结构场分析中仅有扭矩载荷，热-结构耦合场分析中包含扭矩及温度载荷。

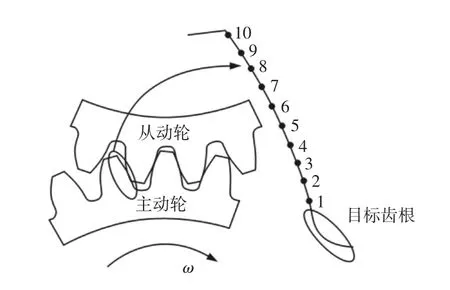
图7 齿轮不同啮合位置Fig.7 Different Meshing Positions of Gears

现对比两种情况下目标齿根的齿根应力分布云图，如表3所示。

表3 各啮合位置齿根应力分布形式对比Tab.3 Contrast of Root Stress Distribution in Each Meshing Position

由上表可知，在啮合位置由齿根向齿顶变化的过程中齿根最大应力由两端逐渐向中部扩散。在结构场中其扩散程度比较明显，在接近齿顶啮合区域附近的齿根最大应力出现在中间区域；而在热-结构耦合场中虽然也有向中间区域扩散的趋势，但其扩散比较慢，而且其最大应力始终是在两端比较明显。对两种情况下的齿根应力最大值距齿轮端面的距离进行测量后，得到表3中右侧两列的结果。由测量结果可知在结构场中的最大应力由齿端附近逐渐向中部移动，而在耦合场中的齿根最大应力均在距齿端1mm附近。这主要是由于齿根受热膨胀产生的拉应力与结构载荷产生的拉应力叠加的结果。现对两种情况下目标齿根的齿根应力最大值进行分析，如图8所示。

图8 各啮合位置的齿根应力最大值Fig.8 The Maximum Value of the Root Stress in Different Meshing Positions of Gears

上图中的啮合点1、2、3、4属于双齿啮合区，此过程中主动轮齿根位置首先进入啮合，啮合点逐渐远离齿根，最大应力值逐渐增大；啮合点5、6属于单齿啮合区，此过程中的啮合位置主要在节圆区域附近，齿面的齿面的啮合力变大，导致齿根最大应力会有明显的增大；啮合点7、8、9、10又属于双齿啮合区，此过程中的啮合力降低，啮合位置是逐渐向齿顶移动，所以齿根应力最大值会有所降低，但仍大于4点之前的值。无论是结构场还是热-结构耦合场均符合上述规律变化，但是将两种情况进行对比，可以发现：热-结构耦合场中的齿根应力最大值普遍小于在同一啮合位置的结构场中的值。这主要是齿根过渡区在温度的影响下产生热膨胀变形从而改变其初始的几何特性，即齿根轴向的热变形使齿根的宽度增加，齿根径向的热变形使齿根曲线的曲率半径增大，从而减弱了齿根的应力集中。

5 结论

（1）经计算齿轮本体温度的高温区主要集中在工作面的中心部位，低温区主要是在非工作面的齿根过渡区。（2）齿轮齿根在受热载荷的影响下其齿根两侧邻近齿轮端面及齿轮基圆区域的热应力值比较大。（3）由于温度载荷产生的热应力的影响，热-结构耦合场的齿根应力分布形式较结构场有明显区别，结构场中的最大应力区由两端向中部过渡，热-结构耦合场中的最大应力虽有过渡趋势但其两端始终为应力最大值的主要区域。（4）由于齿根过渡区受热变形导致在其区域内的几何特性发生改变，热-结构耦合场中分析得到的齿根应力最大值普遍小于结构场中的结果。