笃定前行的黎蔓猜想

陈蓓菲

（福建农林大学计算机与信息学院，福建福州 350002）

1 黎蔓猜想

黎蔓在《论小于给定数的素数个数》的著名论文中提出了六个猜想，其中难以证明又无法推翻的黎曼猜想, 是关于黎曼Zeta 函数的零点分布的猜想。黎曼Zeta 函数如下所示：

黎曼Zeta 函数有两种零点，一种是位于实数轴线上的零点，被称为平凡零点，另一种是位于其他复平面区域上的零点，被称为非平凡零点，目前数学家已经证明这些非平凡零点全部位于实部区间为0 到1 的复平面内，而黎曼则大胆猜想，这些非平凡零点全部位于实部为1/2 的一条直线上。

所有非平凡零点都位于实部为1/2 的直线上，是一个尚未得到严格证明的猜想，但数学家们采用大型计算机计算，至今找到的上万亿个非平凡零点的确都位于这条直线上，无一例外。

不止如此，黎曼猜想还跟幂律分布有关。

我们都知道幂律分布是指：

其中x 如果只能取1,2,3,...,n 的整数，c 为归一化常数，满足：

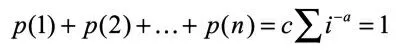
质数分布没有简单规律，但质数出现的频率跟黎曼Zeta 函数紧密相关。有数学家甚至认为黎曼猜想与强条件下的质数定理是等价的。目前已经验证了前1 500 000 000 个质数对这个定理都成立，但至今没有完全证明。黎曼猜想得证，对质数研究、数论研究意义重大。

黎曼猜想对许多数学领域都意义重大，质数分布只是其中一个。有上千个数学命题都建立在黎曼猜想为真的基础上。多数数学家认为这个猜想是正确的，如果黎曼猜想被证伪，数学体系将失去重要根基。

一百多年来，在黎蔓猜想上科学家们前仆后继争先研究，不知道倒下了多少个学者，历史的脚步来到了21世纪，作为菲尔兹奖和阿贝尔奖双料得主，Michael Atiyah 爵士声称证明了黎蔓猜想，他已经功成名就，而且培养出许多优秀的年轻学者。如果真的证明了黎曼猜想，那Michael Atiyah 就会登顶最伟大数学家的行列中，目前，他的证明已然显现在数学家们的眼中。

2 拟合函数

我们来把问题推进一点点，用某个函数来拟合小于给定数的个数，勒让德和高斯分别做出了贡献，给出了拟合函数。

假设L(x)为不超过x 的素数个数，则小于100 的素数有25 个，即L(100)=25，同样的，我们可以算出小于1 000，小于1 000 000 的素数个数，用上述计算机程序可以算出小于等于任何一个给定数的素数个数，L(1 000)=168，L(1 000 000)=78 498。

大约在1800年，勒让德首先观察了如上结果，得出了一个重要猜想，对于足够大的数x，L(x)逼近于下式：x/(log(x)-1.083 66)，这就是勒让德给出来的拟合函数，此处log(x)表示x 的自然对数。此后高斯又独立地建议了一个类似而并不与它相等的公式，他们看出各区间的素数似乎和函数log(x)有关，当时认为这个关系简直难以理解。

自然对数函数log(x)出自微积分中有关生长和衰亡的问题，例如，设想一笔借款，利率150%，一点一点地利上加利逐渐增长，于是log(x)代表一元钱变成x 元所需的年数，数学家把复利中钱数增长的过程叫作“指数增长率”，它可应用于各种不同的问题，如人口增长，放射性衰变，物体冷却以及其他高利率问题。

综合勒让德和高斯猜想，L(x)可以用x/log(x)来逼近，x 数字越大逼近得越好，高斯不仅是一位数论专家，他还建立了数理统计，并应用于天文和素数计数这样两个不同的问题。高斯用现今统计学家所谓的“最小二乘法” 分析了素数公式中误差的性质，他的结果表明，x 足够大时误差极小。

这个“素数定理”（1800年时还是猜想）作为最著名的猜想而震惊数学界。这个方程的一端是素数个数，另一端来自微积分的函数log(x)，并且和人口增长有关，这是离散与连续的“不解之缘”。

对于勒让德—高斯猜想的证明，五十年间毫无进展，首先在这个方向作出贡献的是切比晓夫，他在1848年和1850年相继得到了一些结果，但是，终因问题没有得到彻底的解决而被放弃，英国数学家西尔凡特也曾致力于“素数定理”的研究，而真正解决问题的是阿达玛和普辛，他们几乎同时于1896年各自独立证明了“素数定理”，但是，前人的功劳不可否定，这就是在1859年，黎蔓那篇题为《论小于给定数的素数个数》的著名论文，为阿达玛证明“素数定理”铺平了道路，黎蔓在《论小于给定数的素数个数》的著名论文中提出了六个猜想，许多科学家力图证明黎蔓论文中所表达的主要结果，但都徒劳无功，终于在黎蔓的论文发表三十五年后，阿达玛首先获得了重要突破，证明了其中的三个猜想，不久，阿达玛和普辛，他们几乎同时于1896年各自独立证明了“素数定理”，他们的证明巧妙运用了黎蔓的思路，以后，另一位数学家蒙镐特证明了黎蔓论文中的另外两个猜想，最后遗留下来的一个就是迄今仍未解决的黎蔓猜想。

3 计算机程序与结果

我们说问题的本身，小于或等于给定数的素数个数本身就是小于给定数的，如给定数100，小于100 的素数个数25 个，小于给定数100，因为，只有奇数才有可能是素数，所以，去掉偶数，剩下一半的奇数，而奇数中又不全是素数，所以，小于给定数x 的素数个数一定小于x/2，我们在下面给出Mirosoft Visual C++ 6.0 计算机程序和相应的结果。

设给定数x=1 000，有如下计算机程序。

对于给定数x=1 000，结果如下：

给定一个正整数x，寻找小于等于它的素数

2 3 5 7 11 13 17 19 23 29

31 37 41 43 47 53 59 61 67 71

703 79 83 89 97 101 103 107 109 113

127 131 137 139 149 151 157 163 167 173

179 181 191 193 197 199 211 223 227 229

233 239 241 251 257 263 269 271 277 281

283 293 307 311 313 317 331 337 347 349

353 359 367 373 379 383 389 397 401 409

419 421 431 433 439 443 449 457 461 463

467 479 487 491 499 503 509 521 523 541

547 557 563 569 571 577 587 593 599 601

607 613 617 619 631 641 643 647 653 659

661 673 677 683 691 701 709 719 727 733

739 743 751 757 761 769 773 787 797 809

811 821 823 827 829 839 853 857 859 863

877 881 883 887 907 911 919 929 937 941

947 953 967 971 977 983 991 997

小于正整数x 的素数的个数一共有168

黎蔓，1826年生于德国汉诺威的一个小村庄，黎蔓先在柏林大学学习，后进哥廷根神学院，不久转学数学，师从名师高斯和韦伯。名师出高徒，1851年，在高斯的指导下，以其才华横溢的论文，在哥廷根大学获得博士学位。1859年继承了荻利克莱的席位，荣任哥廷根大学的教授，当选为德国科学院院士，为了说明他自己的才能，在德国科学院院刊上发表了题为《论小于给定数的素数个数》的一篇著名论文，提出了空前重要的猜想——黎蔓猜想。1866年因患结核病卒于意大利北部的一个疗养胜地。整个数学界从此失去了一位最富有创造性、远见卓识的天才人物。他在《论小于给定数的素数个数》一文中，共提出了六个猜想，至今罕见被证明，这是黎蔓猜想笃定前行的理由，因为，难！难以被证明！难倒了一代又一代的数学家！笔者只是在他的猜想里加上时代进步的印记，用了计算机程序，希望有所助益。