高职土木类工程力学课程中重点与难点的分析

夏 璐

(安徽水利水电职业技术学院建筑工程学院，安徽 合肥 231603)

工程力学课是高职土木类专业开设的一门专业基础课。其研究对象单一,均为杆系结构;其研究内容是最基本的受力、变形及破坏规律。该课程为土木类的后续课程如钢筋混凝土设计原理、钢结构等专业课程奠定一定的力学理论基础。该课程在高职类院校中目前处在“两头难”的状态,教师教授困难、学生习得困难。所以如何教好这门课是摆在教师面前的重要课题。

1 工程力学课程重点与难点的教学要点

工程力学内容多、繁,知识点本身较为枯燥。本文以高职土木类专业为例,将该课程的重点与难点内容进行梳理、归纳成“1+3”的教学内容。所谓“1+3”是指“1条主线,3大模块”。如图1所示。

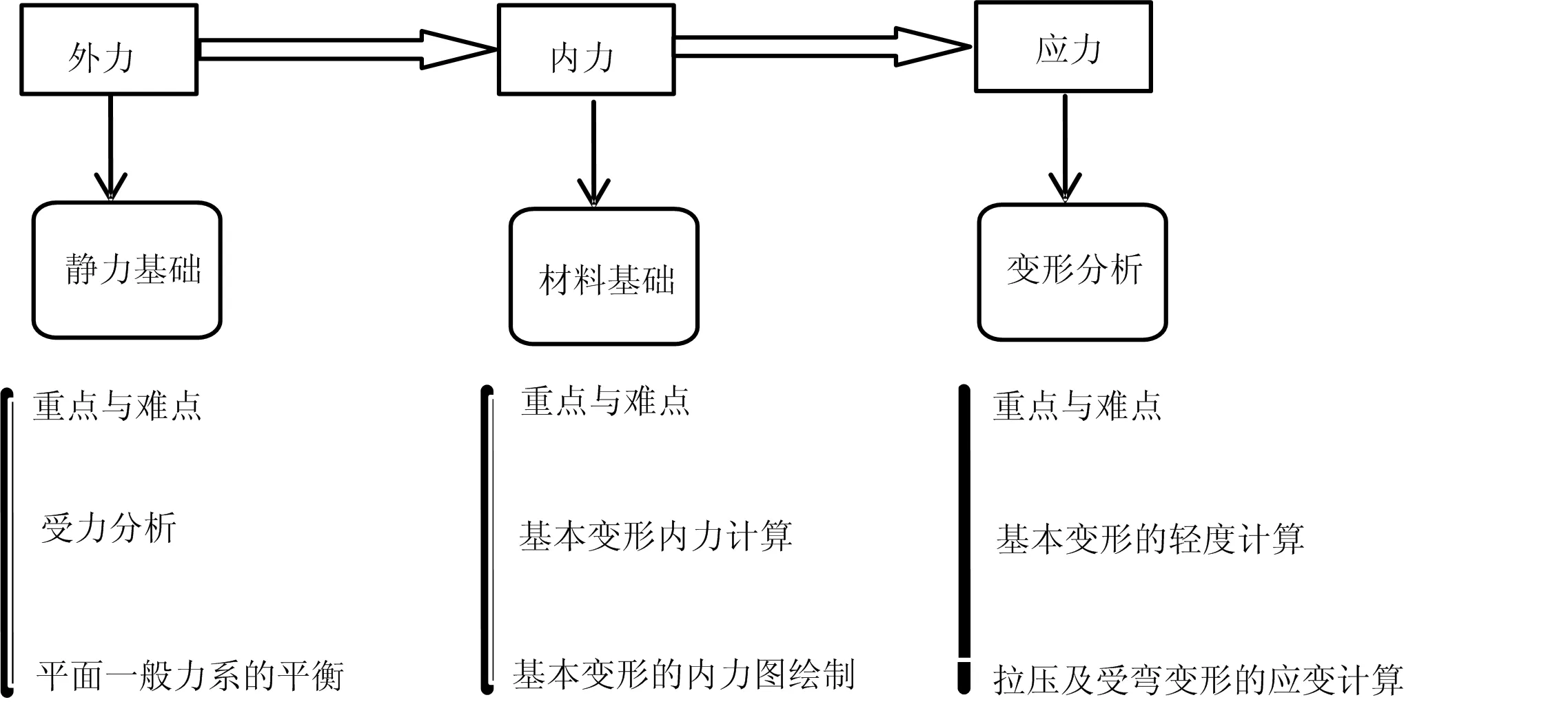
图1 “1+3”教学内容

2 静力平衡问题的三要素和平面一般力系的平衡求解

2.1 第一要素——受力分析图

画受力分析图的关键在于准确无误的判断约束反力。约束反力就是阻碍物体运动的力,力的方向(包括方位和指向)总是与物体运动方向或运动趋势方向相反。判断约束反力方向时,只需要了解周围物体限制了物体的哪个方向的运动或运动趋势即可。

为了方便学生的记忆,将约束分为5大类进行讲授,即柔体约束、光滑接触面约束、链杆约束、圆柱铰链约束及支座约束(固定铰支座、可动较支座、固定端)。每类约束结合实际从构造、约束特点及约束反力进行阐述。例如柔体约束,可结合教室的吊灯、快递运输货品的传送带等说明该约束只拉不压的约束特点,从而用简单的7个字“沿柔体,背离物体”来描述约束反力方位和指向;需要强调的是,画约束反力的个数不能少。前两类约束是明确方位和指向的1个约束反力,后面3类均是指向假设的约束反力。链杆约束是方位明确指向假设的1个约束反力,圆柱铰链约束是2个分力(x方向、y方向)表示的约束反力,固定铰支座可类比圆柱铰链,可动铰支座可类比光滑接触面约束,固定端可结合室外的电话杆、路灯、树木等说明该约束有3个约束反力(x方向、y方向、平面转动)。

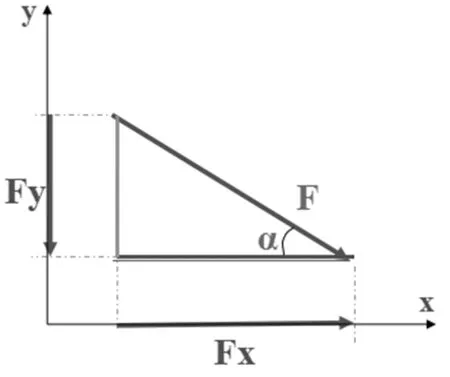
图2 正交分解投影示意图

2.2 第二要素——力的投影

静力平衡问题的实质就是将力先正交分解再合成的过程。正交分解就是投影的过程。对学生来说,画投影没问题,算大小就有些问题了。为了方便记忆,我们将投影大小计算,总结为“邻边余,对边正”。合力为一斜边,2投影为2直角边,如图2所示。在给定角度α的情况下,判断出邻边cosα和对边 sinα。不用死记硬背投影公式Fx=±F cosα;Fy=±F sinα。

2.3 第三要素——力矩与力偶

力矩与力偶有很多相似之处,作用效果相似,计算公式一样,学生常常分不清楚。笔者从其概念出发进行区分,力矩是点和力的关系(点是矩心),力偶是2力(等值,反向,平行,不共线)的关系。力矩在计算时要会合理利用合力矩定理,便可以将复杂的力臂求解过程进行简化。力偶在很多情况下都是直接给出数值的,学生往往就会忽略力偶特有的性质,力偶只能与力偶合成与平衡;力偶的大小恒等于力偶矩大小,与矩心位置无关。另外,在力的平移定理里,力偶的大小和方向用力矩的大小和方向来替代的,这点一定要点出并强调。

2.4 平面一般力系的平衡求解

静力平衡的三要素可类比“+-×÷”,那么求解平衡问题就是由三要素构成的混合四则运算。求解一般平面力系的平衡问题,就是对物体建立平衡方程的过程,解题步骤简化为3步走,“1取、2画、3列”。

(1)取。指的是选取研究对象,研究对象的选择关乎着解题的速度和准确率。对于单个物体的研究对象自不必说。对于物体系统的研究对象,一般会遵循“整——分、分——整”原则和“主动力作用的特殊构件优先”的原则。“整——分、分——整”原则是指建立的平衡方程最多是3个(最多解3个未知数),在取整体或分部的作为研究对象时,分析其受力的未知个数是否小于等于3个和有N-1个力交于一点或与轴有垂直。“主动力作用的特殊构件优先”是指在选取了多个符合其受力的未知个数是否小于等于3个的构件,优先挑出有主动力的2力构件或3力构件。

(2)画。指的是画研究对象的受力分析图,受力分析图正确与否直接关系着解题的正确与否。基本步骤是“1分1力1约束”。1分是画隔离体,也就是去除周围所有约束的研究对象;1力是画主动力,研究对象上的主动力,大小方向切不可变。1约束是画约束反力,这也是学生最容易出错的地方,切不可想当然的去画反力,一定要对照5大约束类型的约束特点来画。

(3)列。指的是列平衡方程,列平衡方程必须建立1个坐标系,坐标系的原点便是简化中心,建立坐标系原则是“1个方程解1个未知数”,如何做到1个方程解1个未知数,较多的力与坐标轴有特殊关系(平行或垂直)。对于一般平面力学平衡问题求解时,坐标系一般不画出,只是假想建立。列出3个平衡方程,平衡方程有3种形式(一般式、二矩式、三矩式),为了降低难度,用最少的理论来求解平衡问题,选用一般式就足够了,即∑X=0,∑Y=0,∑M0=0。

3 简易法画内力图

3.1 杆件轴向拉压的简易画法

在杆件外力已知的情况下,运用直接运动法来画轴力图。可用口诀记忆:① 从左往右,从零到零;② 段内无力,拉直线;③ 遇集中力,突变,左上右下,突变值等于集中力大小;④ 遇均布荷载,一斜直线,左上右下倾斜,斜线的起止点差值等于均布荷载大小;

具体的作图过程如下:如图3所示,已知F1=10kN,F2=20kN,F3=35kN,F4=25kN。从杆件的最左边画起,即坐标轴的原点。遇到集中力F1,指向左侧,向上突变10kN(使原点由0到达10的位置),AB段段内无荷载拉直线;B点处又遇一集中力F2,指向右侧,向下突变20kN(点已在10的位置现在往下变20到达-10),AC段段内无荷载拉直线;C点处又遇一集中力F3指向左侧,向上突变35kN(点已在-10的位置现在往上变35到达25),CD段段内无荷载拉直线;D点处又遇一集中力F4,指向右侧,向下突变25kN,(点已在25的位置现在往下变25归0)。

值得提醒学生的是:① 直接运动法,归零的含义是Y轴坐标为0,可以检查轴力图的正确性;② 左上右下的口诀容易记混淆,可以以第1个力为方向为参照,其余力与第一个的力方向同,突变同,方向反,突变反。如图2所示。第1个力F1背离截面为正,向上突变,F2与F1方向反,突变反;F3与F1方向同,突变同。

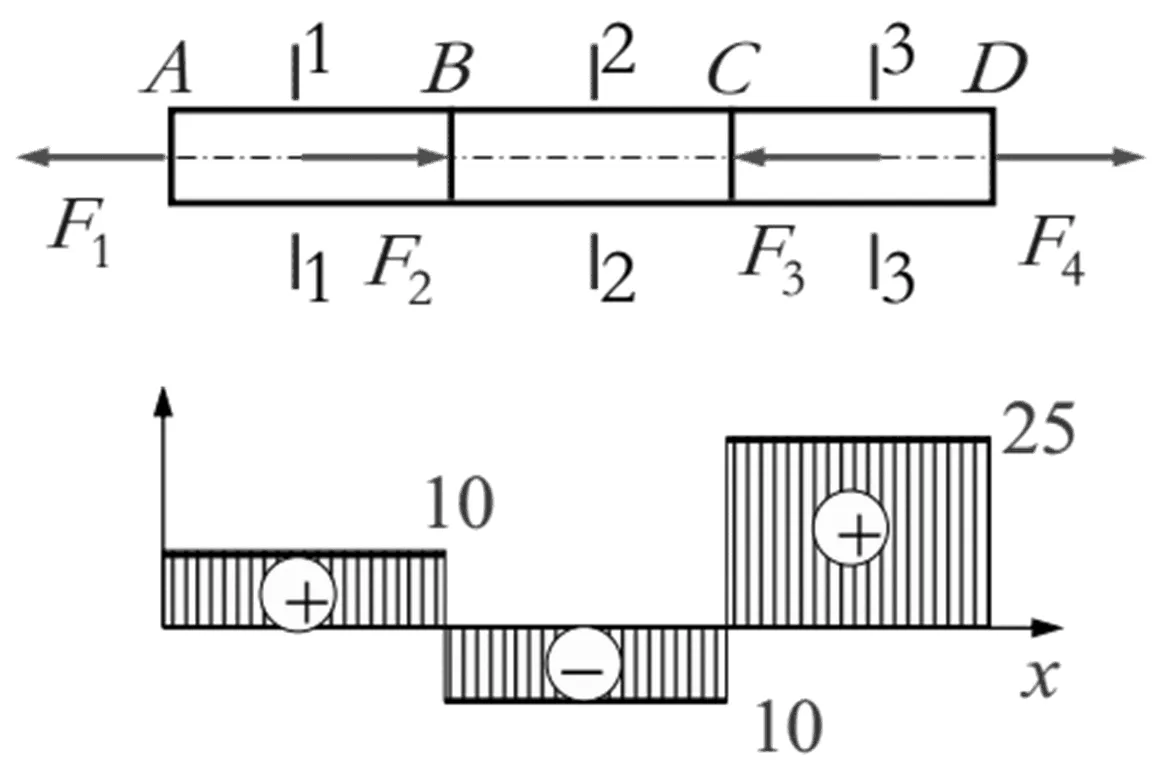
图3 轴力图绘制

3.2 杆件扭转的简易画法——左手法则画图法

在杆件外力偶已知的情况下,运用左手法则来画扭矩图。有以下口诀便于记忆:① 从左往右,从零到零;② 段内无力偶,拉直线;③ 遇集中力偶,突变,左手法则(4指为转动方向,大拇指为X轴方向),与X轴正方向同向上突变,反之向下;突变大小等于力偶大小;④ 遇均布力偶,一斜直线,左手法则(四指为转动方向,大拇指为X轴方向),与X轴正方向同向右上倾斜,反之向右下;斜线的起止点差值大小等于均布力偶大小;

具体的作图过程如下:如图4所示,从杆件的最左边画起,即坐标轴的原点。遇到集中力偶90,左手四指与力偶弯曲方向同,大拇指指向与X轴正方向反,向下突变90,(使原点由0到达——90的位置),第一段段内无荷载拉直线;又遇一集中力偶190,左手四指与力偶弯曲方向同,大拇指指向与X轴正方向同,向上突变190(点已在90的位置现在往上突变190到达100),段内无荷载拉直线;又遇一集中力偶60,左手4指与力偶弯曲方向同,大拇指指向与X轴正方向反,向下突变60(点已在100的位置现在往下突变60到达40),段内无荷载拉直线;最后一力偶40,左手四指与力偶弯曲方向同,大拇指指向与X轴正方向反,向下突变40(点已在40的位置现在往下突变40归0)。

采用左手法则画扭矩图时,必须强调的是,内力扭矩T的正反方向的判断是右手法则。

3.3 梁内力图的简易画法

(1)梁剪力图的直接画法。在杆件外力已知的情况下,运用直接法来画剪力图。可以参照轴力图及扭矩图。① 从左往右,从零到零;② 段内无力,拉直线;③ 遇集中力,突变,突变方向与力方向同,突变值等于集中力大小;④ 遇均布荷载,一斜直线,倾斜方向与力同,斜线的起止点差值等于均布荷载大小;⑤ 遇见力偶,当未见。

具体的作图过程如下:如图5所示,从杆件的最左边画起,即坐标轴的原点。A点处一集中力,往上突变9.33kN,B点的集中力偶在画剪力图时可当其不存在,AC段内拉直线;CD段为一均布荷载,应向右下方倾斜,D点与C点差值等于均布荷载大小,QC=9.33kN,QD=-14.67kN,D点上的力可以作为是否归零的依据,也是判断内力图是否正确的依据。

(2) 梁弯矩图的控制截面画法。梁的弯矩图与剪力图是相辅相成的关系,密不可分。弯矩图的画法与轴力、扭矩及剪力图的画法有较大的差别,首先,正负号的规定上,弯矩图无正负号的划分,弯矩画在受拉一侧;其次,在划分区段上,遵循的基本原则是满跨、单一。满跨是指段内均布荷载的长度就是段长;单一是指段内只有一种荷载。具体分段步骤是:1、找控制点(集中力作用点、均布荷载的起止点、集中力偶的左右点,剪力为零点);2、用点将杆分段。3、根据每区段的端点及剪力为零点计算弯矩值。控制点(每区段的端点及剪力为零点)的弯矩值计算采用直接的虚拟杆件法来求解。

具体做法如下:如图5所示,先将ABC杆件的控制点找出(先观察剪力图有没有段内为零点)。分别是:A点,B点左、右点、C点的左点。根据虚拟杆件法求解各点弯矩值。

MA=0,A点为杆件起点,过A点的假象截面截开,取左半部分为空,所以为零。或者可以理解成所有内力图均从零开始。过B左点的假想截面截开,取左半部分,从哪里截开,手就握住哪里,1根虚拟的AB杆在手上。从左往右看荷载对B左点的力矩代数和,此处力矩方向是下拉为正。MB讅=FAy×1=9.33kN·m,结合剪力图,可知,弯矩图的AB左这段为一条斜直线,右下倾斜。B点处的集中力偶处发现突变,逆上顺下,MB右=9.33-8=1.33kN·m;BC段为一右下倾斜的斜直线,C点处一假想截面截开,取左半部分,从哪里截开,手就握住哪里,1根虚拟的AC杆在手上。从左往右看荷载对C点的力矩代数和,下拉为正,MC=FAy×2-8=10.66kN·m;CD段为一抛物线,剪力为零点为极值点,在极值点处一假想截面截开,取右半部分,从哪里截开,手就握住哪里,1根虚拟的De杆在手上。均布荷载上拉为负,集中力下拉为正,MQ=0=FBy×2.44-6×2.44×1.22=17.93kN·m;D点为铰弯矩为零。

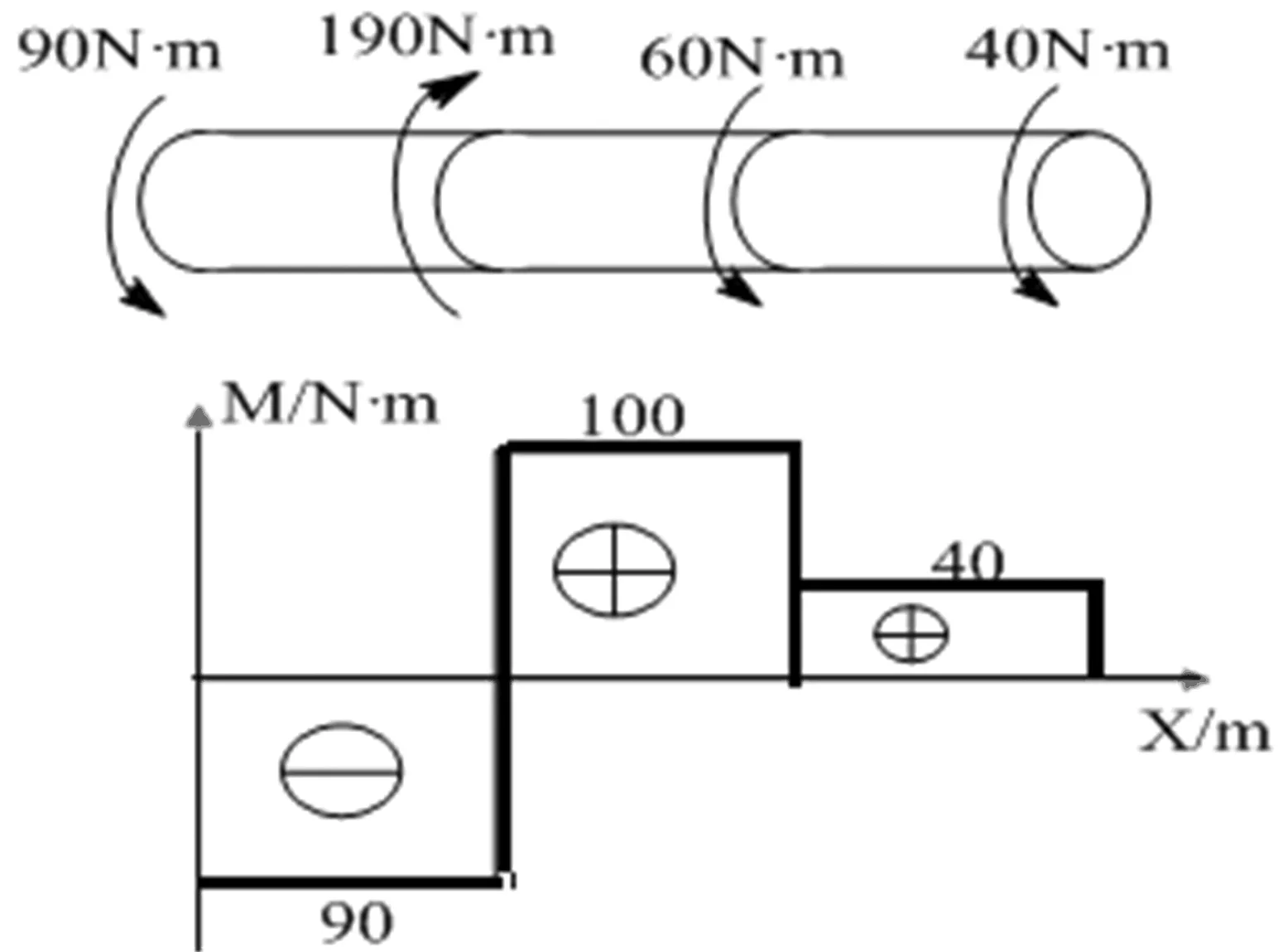
图4 扭矩图绘制图

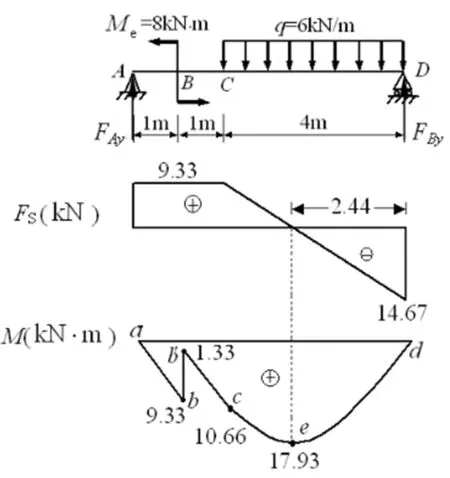
图5 梁的内力图绘制

4 4种变形的应力及应变

研究材料的强度、刚度、稳定性等力学性能,为工程构件提供设计依据及计算方法是工程力学课的重点也是难点,对于高职院校的学生来说,应力与应变的计算公式熟记会用即可。4种变形的应力与应变的关系可以类比弹簧的虎克定理公式,即F=kx,应力与应变的关系式是σ=Eε,τ=Gγ。σ,τ可类比F,E,G可类比k,ε,γ可类比x。

轴向拉压的应力要强调条件假设,假设力在横截面上是均匀分布的,从而得到应力计算公式σ=N/A;其应变计算可以用建筑材料上的伸长率来强化记忆,伸长率就是相对变形量就是应变ε=Δl/l;根据应力计算公式、应力应变关系式推导出绝对变形量计算公式Δl=Nl/EA。扭转及弯曲的应力应变的教学过程可以参照轴向拉压的教学过程。

5 结束语

虽然工程力学是一门难度较大课程,但只要抓住课程的重点与难点,通过科学、高效的教学方式,有效的学习方法,一定能教好学好。