提高农村小学六年级学生运算能力的有效方式研究

吴燕贞

摘 要：运算能力核心素养的形成有赖于教师在每个课堂中坚持不懈的启发、渗透，更有赖于一套高效低负、操作性强、可推广的运算能力训练机制的形成与实施。从提高农村小学六年级学生运算能力方面思考并展开研究，依据《义务教育数学课程标准》与《广州市义务教育阶段学科学业质量评价标准》要求，通过多次制订、修改训练计算的方案，运用“强化”的心理学理念，学生通过每天累积一定的练习量，逐渐从量变到质变，达到提高运算能力的目的。

關键词：运算能力；行动研究；训练机制

一、新课标对六年级学生运算能力的要求

《广州市义务教育阶段学科学业质量评价标准》中提到，素养是指人通过长期的学习和实践，在理论、知识、艺术、思想某一方面所达到的程度。其内涵包括：其一是注重平时的养成，强调渐进性；其二也注重结果，强调形成性。教书育人是教师的本职工作，要取得良好的教育教学效果，就要遵循教育的基本原则，本着对学生负责任的理念，思考因材施教的方法，希望尽最大的努力，帮助学生学有所得，让每个学生都在原有基础上有所进步。怎么做才可以提高教学成绩呢？小学阶段数与代数中数的运算占分值的比重很大，提高全班整体成绩的捷径无疑是提高全班学生的运算能力。怎样才能提高学生的运算能力呢？

运算能力核心素养的形成有赖于教师在每个课堂中坚持不懈的启发、渗透，更有赖于一套高效低负、操作性强、可推广的运算能力训练机制的形成与实施。六年级关于运算方面的内容有“分数乘法”和“分数除法”，笔者打算根据自己的研究课题《培养小学数学核心素养之运算能力的实践与研究》出发，从提高运算能力方面思考，通过制订训练计算的方案，运用“强化”的心理学理念，希望通过每天累积一定的练习量，逐渐从量变到质变，达到计算又准又快的效果。如果能够使全班学生的运算过关，并能顺势迁移到问题解决等方面，很容易让原来失去学习信心的学生重新对数学感兴趣，降低班级低分率，提高全班的平均成绩，从而完成教学任务。基于上述的背景和思考，开展如下的行动研究。

二、提高运算能力的教学方式行动研究

（一）第一次行动与反思

1.方案的制订

心理学认为，强化是塑造行为和保持行为强度的不可缺少的关键。美国著名心理学家斯金纳认为，行为之所以发生变化，是由于强化作用。如果一个行为发生后，接着呈现一个强化刺激，行为的强度就会增加。基于强化理论的认识，笔者制订了以下训练的方案，希望通过每天口算训练，强化学生的口算能力。

（1）时间：每天数学课前3分钟。

（2）内容：共8至10道口算题。

（3）人员：数学科代表作为听算员，全班听算。

注意事项：科代表必须提前一天准备听算内容。听算结束后，由一名同学说答案，全班订正改分。星期五全班收检。

2.方案的实施

小学数学六年级上册的第一单元是“分数的乘法”，第三单元是“分数的除法法”，这两个单元中都有混合运算。做好六年级的计算，五年级分数加减运算和约分的知识是基础，直接影响学生对混合运算的学习。于是我分成两个步骤实施方案。第一步骤：第一个星期，没学分数乘法之前，我安排科代表出题：分数加减法题10道。第二步骤：开始学分数乘法的内容时，科代表的出题改为：分数加减法题5道，分数乘法题5道。以此一边复习五年级的知识为学习混合运算做好准备，一边巩固新知为后续的学习打下扎实的基础。

3.考查与反思

听算第一天，A班的科代表出10道分数加减法口算题，学生一边听，一边算。结果全班大约有二十个人跟不上速度，反馈说“科代表读得太快”。随即改进为科代表在念完每道题后，心中默数8秒后再念下一题。当科代表放慢速度以后，还是有十人以上跟不上速度。计划3分钟的课前口算，等大部分学生计算完毕时耗时10分钟，还有大约十五个学生无法完成，等待别人订正答案时，直接抄上去。B班听算的情况稍微比A班好一点，不会算的人在十个人以内，耗时稍微短一点，用了8分钟。

听算第二天，A班和前一天一样，不会算的学生，基本都在等答案，如果读题速度快一点，有的学困生甚至写不出题。B班的情况也是基本和前一天的情况相当。两个班的听算和订正完成，耗时均在10分钟以上。

经过这两天观察，发现课前的训练不能达到预期的“强化”效果，或者说只对部分优秀学生达到了“强化”效果。第一天耗十分钟评讲，第二天情况依然没多大改观。

此时笔者才恍然大悟，不是学生记不起来，是学生根本不懂。如果学生面对不懂的知识又无法解决，这种挫败感长期持续下去必然会使学生失去学习的耐心和信心，造成厌学。而且如果每天继续这样听算、评讲，就剩下半节课讲新课了，新授的时间不能保证，乘法学不好，除法紧接着也不能学好了，对应的混合运算和解决问题也不能学了。因此，笔者必须立刻调整方案。

（二）第二次行动与反思

1.方案的制订

这次制订的方案重点从帮扶学困生的角度考虑，首先降低训练题型的难度，比如10道题中至少有5道题是他们觉得有希望“做得对”的题目。同时既要保证每天进行口算训练，又要保证新授课的时间。另外，考虑到两个班的学生当中还有相当一部分学生不会算，处于“等答案”那种状态。因此教师要注意不能太急于公布答案，需要给予其充分的做题时间。根据农村学校的作息与城区学校不同的特点。笔者随即将训练时间和形式作了调整，形成第二次方案：

（1）时间：每天午饭后的自习时间约10分钟。

（2）内容：共10道口算题。

（3）人员：数学科代表出题，全班计算。

注意事项：科代表必须提前一天准备口算内容，抄在黑板上。口算时间由学生自己安排完成。午休结束前，由科代表出示答案，全班订正改分。星期五全班收检。

2.方案的实施

训练时间改在午休，由科代表出题，全班抄题完成。在题型的选择方面，要求科代表出10道口算题，分别是同分母分数加减2题、异分母分数加减2题、分数乘整数6题（属于新授内容）。全班完成，午休结束前，全班订正答案。方案实施两天，星期五回收检查整体情况。

3.考查与反思

训练方案经过调整，既保证了数学课的新授时间，又保证每天有10道题的口算训练量。题型方面更有针对性，对于学困生而言，既能复习五年级落下的知识，又能巩固六年级新授的知识。计算的时间比较充足，大部分学生都能完成的。前期部分学生抄答案的现象有所改善，但仍然存在。对于学困生而言，没有老师的及时评讲，原来不懂的还是不懂。

学生在学习上的成功感，是其持续学习的有效内驱力。实践证明，持续的失败会让人丧失继续行动的信心，“让学生跳一跳就可以摘到果子，才能尝到拥有果子的成功感，才有信心进行下一次的尝试”。前一个方案，让知识有欠缺的学生感到更紧张，增加了学习的压力，形成了学习的阻力。不但没起到训练的效果，反而起了反作用。这次调整方案以后，能使优生快速完成训练任务，达到训练目的；也能使学困生有比较充足的思考时间，相对轻松地完成训练。可是对于重度学困生而言，不懂的还是不懂，没有老师个别帮扶，仍然有强烈的挫败感，表现出来的行为是不愿意思考，直接抄袭别人的答案。要怎么做能更好地帮助学困生呢？笔者带着思考进行了第三次行动研究。

（三）第三次行动与反思

1.方案的制订

这次方案的制订还是重点考虑如何更好地帮扶学困生。午休自习的训练方式不作改变，题型重点也是4道题复习加减，6道题巩固新授知识。改变的其中一点是加上老师或同学的帮扶。具体方案如下：

（1）时间：课前2分钟和每天午饭后的自习时间约10分钟。

（2）内容：课前2分钟做2道口算题，午休自习做10道口算题。

（3）人员：①课前：老师出题，全班做。②自习：数学科代表出题，全班计算。

（4）课前老师出的题型是“一新一旧”混搭，“新”——前一天的新知，“旧”——五年级的旧知。做完马上讲评计算方法，订正答案，时间控制在2分钟内。

（5）科代表提前一天准备口算内容，抄在黑板上。口算时间由学生自己安排完成。午休结束前，由科代表出示答案，全班订正改分。星期五全班收检。

2.方案的实施

课前老师出的题型是“一新一旧”混搭，“新”——前一天的新知，“旧”——五年级的旧知。做完马上讲评计算方法，订正答案，时间控制在2分钟内。有了课前“一新一旧”混搭的训练和老师的及时评讲，大部分学困生感到对于新知的学习容易了。午休自习坚持做10道口算题，随着训练次数的增加，“强化”的效果逐渐显现，好几个学困生感到分数加减法计算逐步上手了。

3.考查与反思

由于老师把控题型的能力比科代表强，课前的训练有更强的针对性，大部分学生感受到计算容易了，算起来就有信心了。使午休自习的计算训练得以有效开展，“等答案”的人少了。随着训练天数的增加、学生训练量的累积，大部分学生在计算上还是有比较大的进步的。

及时评讲，持续训练，从几次检测的数据来分析，这种方案是有效的。要达到突破计算、提高合格率、降低低分率这个目标，在口算训练方面目前算是取得一点成效，但是计算除了口算以外，还有很多类型，例如简便运算、笔算加减乘除，解方程等。需要攻破的关键点还有很多，教师要争取在有限的时间内，让学生做到边学新知边复习巩固旧知。

三、六年级学生运算能力提高的效果及设想

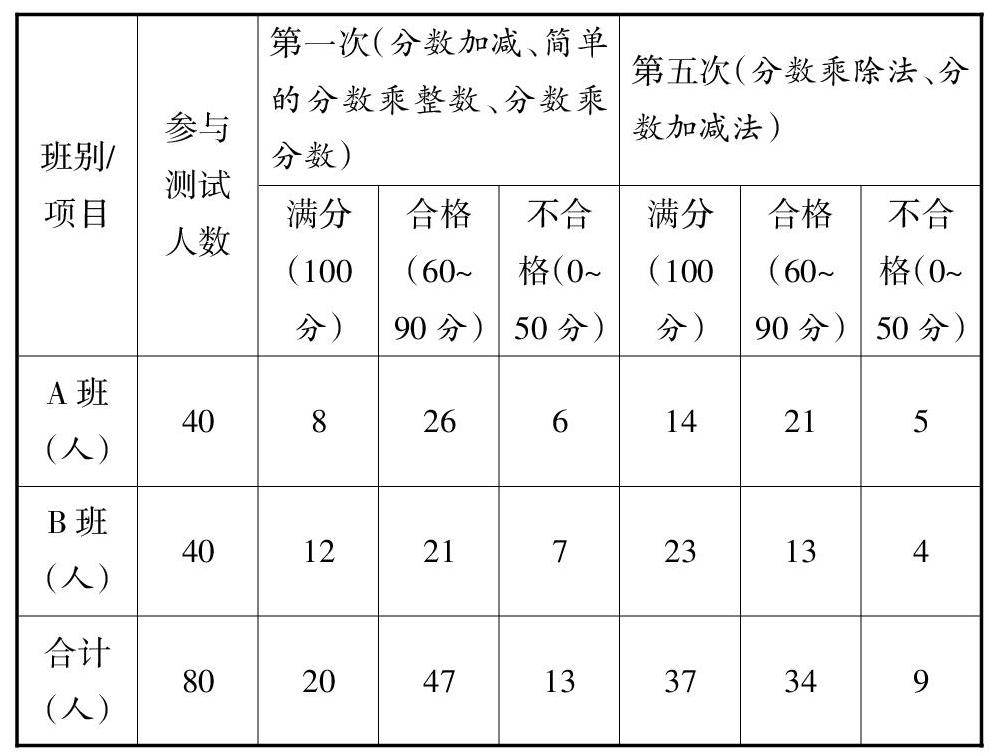
经过三轮行动研究发现，训练的效果是明显的，大部分学生运算能力得到了有效提高。自开展研究以来共做了5次口算检测，就第1次专题检测和第5次检测专题检测列表对比如下：

《义务教育数学课程标准》要求：计算教学旨在培养学生的数感，增进学生对运算意义的理解。现实生活既是计算教学的源头，又是计算教学的归宿。教师应努力为学生提供将所学知识应用到实践中去，以解决身边的数学问题的机会，从而帮助学生了解数学的價值，增进对数学的理解和应用数学的信心，提高学生计算能力。提高农村小学六年级学生运算能力是提高六年级学生数学成绩的关键，教师在保持日常口算训练的同时，还要逐步加强其他方面的训练，如运算定律等，在题型方面还有混合运算、笔算、解方程等。相信只要教师把控好时间和题型，形成并执行有效的训练机制，持之以恒，一定会收到成效的。

参考文献：

巴班斯基.论教学过程最优化.[M].北京：教育科学出版社，2001.