机械侵入荷载下格栅用于防护柔性埋地管道的试验研究
2019-04-22王嘉勇肖成志何晨曦
王嘉勇, 肖成志, 2, 何晨曦
(1. 河北工业大学 土木与交通学院,天津 300401;2. 河北工业大学 河北省土木工程技术研究中心,天津 300401)
当前,随着城市基础设施建设的快速发展,以挖掘机械侵入为主的第三方施工荷载成为国内外油、气和水等埋地管道破坏的主要因素[1-2]。Brooker[3-5]、姚安林[6]、杨建功[7]和李军[8]等先后通过模型试验和数值模拟方法分析了挖掘机斗齿荷载对管道的影响,发现因挖掘机铲尖刚度大,挖掘侵入土体速度较快,而埋地管道常以钢管或塑料柔性管等为主,一旦挖掘机侵入触碰管道极易使其发生变形或破裂,从而引发油气泄漏或爆炸等危险事故。因此,如何针对埋地管道进行防护引起了大量研究人员的关注。土工格栅作为岩土工程加筋材料依靠其造价低、性能好、施工简单等优点在短短几十年的时间内发展迅速,在挡土墙和桥台台背与软基处理和道路工程加固等方面发挥着重要的作用[9]。目前,国内外在土工格栅用于防护埋地管道方面的研究已取得了一定的成果。Selvadura[10]试验指出在埋地管道上方铺设格栅可有效提高承载能力;Hegde等[11]研究了静载作用下土工格栅和土工格室对埋地管道防护减灾性能,指出格栅加筋能够大大降低管道变形、管顶土压力和管道应变;肖成志等[12-13]针对格栅加筋防护HDPE埋地管道开展了静载试验分析,提出了格栅最佳敷设参数。Palmeira[14]试验模拟分析了施工机械侵入筋材防护埋地管道的变形与受力特点。但施工机械侵入时管道破坏机制的研究尚不成熟,且管道设计中尚无相应标准或规范明确挖掘机侵入等第三方施工所产生的影响。因此,针对第三方施工荷载作用对油气管道力学性能的影响亟待研究。本文拟通过室内模型试验,模拟施工机械持续侵入过程,以此分析土工格栅对管道防护性能的影响,并对比分析筋材长度、筋材埋深、间距和层数等对防护效果的影响。
1 土工格栅加筋防护埋地管道模型试验
为了研究施工机械侵入时埋地管道力学响应以及土工格栅对埋地管道的防护性能,这里开展了室内模型试验,如图1所示。模型箱的长、宽和高分别为120、40和100 cm,并参照美国AASHTO(1998)[15]和埋地管道相关规范[16]对具体模型尺寸进行选取。试验通过电液伺服作动器控制力和位移,将长、高和厚分别为20、25和2 cm的钢板于埋地管道顶部地表贯入土层以模拟挖掘机铲斗的持续侵入过程。
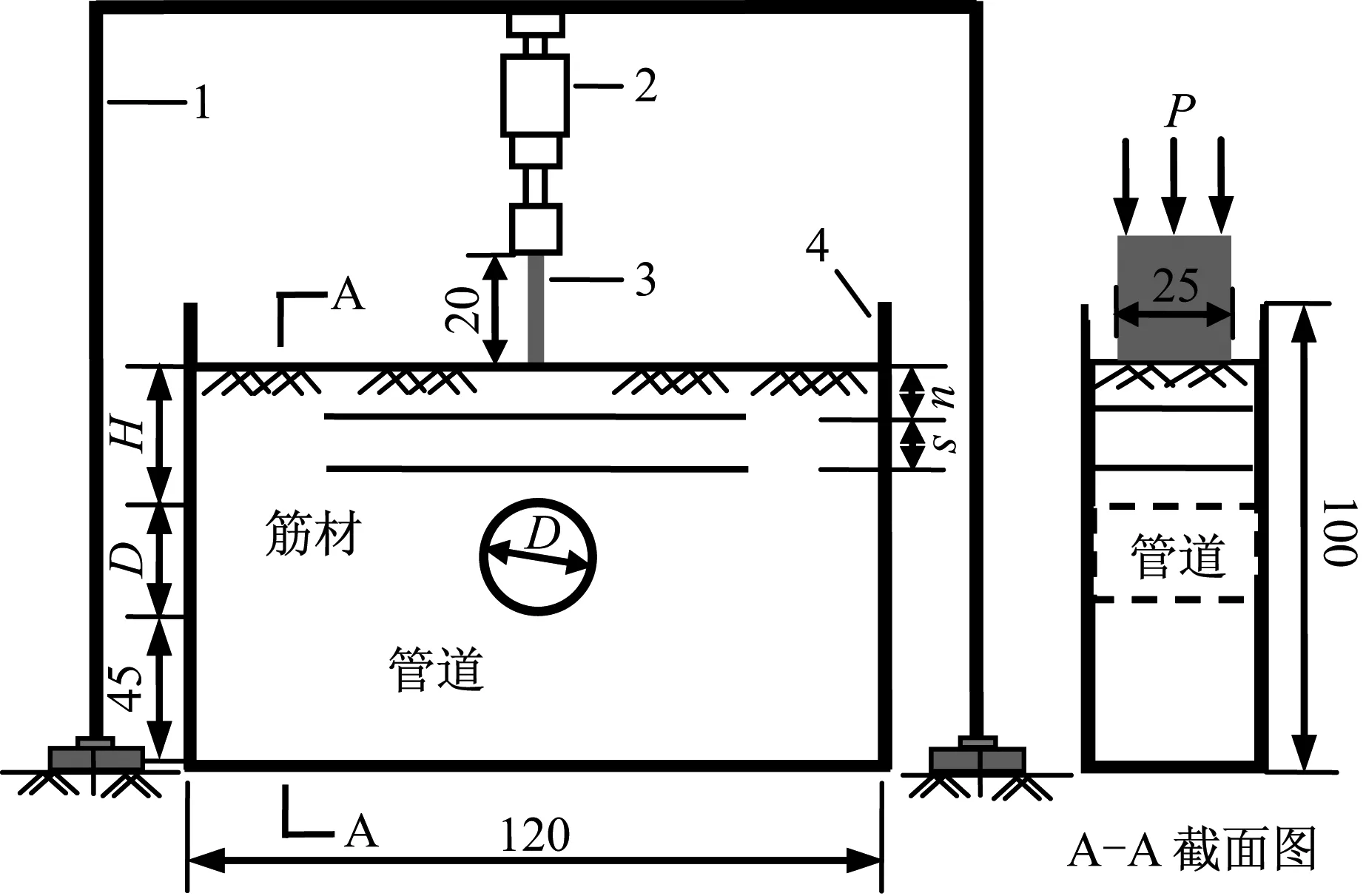
1.反力架;2.电液伺服作动器;3.钢板侵入体;4.模型箱 (a) 试验加载平台系统装置图

(b) 试验现场模型图图1 埋地管道模型试验平台与装置图(cm)Fig.1 Model test platform and device of buried pipe
1.1 回填土
管周填土采用干净河砂,其最大和最小干重度分别19.90和15.63 kN/m3,基于砂土筛分试验得到其颗粒级配曲线如图2所示,不均匀系数Cu为2.65,曲率系数Cc为0.99,土样细粒(粒径小于0.075 mm)含量小于5%,属于级配不良砂土。试验回填砂土相对密实度为70%,按5 cm分层填压,铺设筋材时筋材层及其上下邻层用红色彩砂标示,以便于观察土层沉降,如图1(b)所示。

图2 回填河砂颗粒级配曲线Fig.2 Grain size distribution of river sand for filling
1.2 管道和筋材
选用外径110 mm、壁厚5.3 mm的高密度聚乙烯(HDPE)管道和聚丙烯EG3030双向格栅,管道密度为0.965 g/cm3;格栅极限抗拉强度为30 kN/m,应变为2%和5%时所对应的拉力分别为10.5和21.0 kN/m。
1.3 试验与测试方案
试验在管顶地表采用持续静压钢板侵入体来模拟挖掘机械侵入,图3给出了试验的不同工况。

(a) 模式1(b) 模式2(c) 模式3(d) 模式4
图3 试验与加筋防护模式
Fig.3 Test and reinforcement protection modes
工况1:无筋材防护;
工况2:单层筋材阻挡机械侵入;
工况3:多层筋材阻挡机械侵入;
工况4:筋材分别用于阻挡机械侵入和防护管道。
通过改变筋材的长度L、埋深u、间距s以及层数n等参数,综合分析模拟机械侵入荷载作用下筋材对埋地管道的防护效果。试验重点监测各因素影响下的侵入荷载、管道变形和管道外表面环向应变。模型试验采用自制百分表固定于管道内部,监测管道径向变形U(水平:Uh和垂直:Uv) (如图4(a)所示);同时,沿管周布置8个环向应变监测点(如图4(b)所示)。
试验中按照侵入体贯入砂土的深度Hb进行加载,每次贯入1 cm且每级载荷持续5 min,直至侵入深度达到15 cm(约1.4D)时结束试验,详细试验方案见表1。

(a) 管道径向变形监测(b) 管道应变监测点

图4 管道变形与应变测点布置图Fig.4 Layout of deformation and strains monitoring of pipes表1 施工机械侵入荷载下埋地管道力学机理及防护研究方案Tab.1 Mechanical mechanism and protection research scheme of buried pipes under intrusive load of construction machinery
2.1 筋材长度对加筋防护效果的影响
这里采用单层筋材防护模式,选取管道埋深H/D=2、筋材埋深u/D=1.0,对比筋材长度L/D分别为2、3和4时的加筋效果,结果如图5所示。

(a) P Vs Hb/D
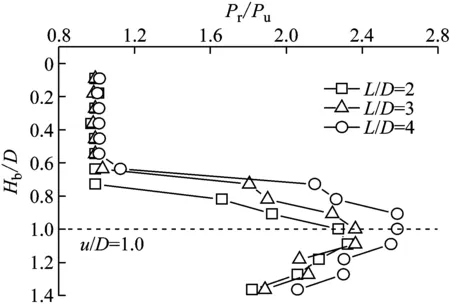
(b) Pr/Pu Vs Hb/D图5 不同筋材长度下侵入荷载随侵入深度的变化Fig.5 Variation of the intrusive load with intrusive depth under different length of reinforcements
图5(a)给出了加筋前、后侵入荷载P随侵入深度Hb的变化曲线;为便于对比,图5(b)对应给出了加筋后与加筋前侵入荷载之比Pr/Pu与Hb/D的关系曲线。由图可知,随着侵入深度Hb/D的增加,侵入荷载P逐渐增大;Pr/Pu整体上呈现先增大后减小的变化趋势,且在Hb=u附近达到极值;当侵入深度Hb/D相同时,筋材越长,Pr/Pu越大。取Hb=15 cm(约1.4D)时分析,L/D由2增加至3时,Pr/Pu(或Pr)增加了3.74%,L/D由3增加至4时,Pr/Pu(或Pr)增加了9.01%,表明随着筋材长度L/D的增加,达到相同深度侵入荷载不断增加,加筋防护效果越好。
究其原因:试验中侵入体贯入时主要受到土体摩擦阻力f和筋材阻碍力Fr的作用,即P=f+Fr。随着侵入深度Hb增加,f和Fr的总作用持续增大,使得侵入荷载P单调递增。其中,当侵入深度较小,如Hb<0.8D时,由于浅层土体自重小,强度低,且此时侵入体距离加筋区较远,因此f和Fr均较小,使得侵入时荷载P很小,加筋效果不明显,Pr/Pu接近1;当0.8D≤Hb≤u=D时,侵入体逐渐接近并达到筋材所在位置,筋材作用也越来越显著,而筋材对侵入体的抵抗作用主要由筋材在土体间的抗拉拔阻力提供,现有研究表明[16],砂土中格栅法向应力越小,拉拔阻力达到峰值时的所对应的拉拔位移越小,由于本文试验中格栅只受到覆土较小的压力作用,因此筋材一旦与土体产生相对滑动其拉拔力已基本达到最大值,从而使得筋材的作用在Hb=u附近发挥至极致,Pr/Pu出现峰值;当Hb>u时,由图6可知,筋材未发生断裂破坏,其与土体发生相对滑动然后随着侵入体一起向下运动,但在此过程中由于加筋作用趋于稳定,Pr增长速率降低,导致Pr/Pu值减小。另外,随着筋材长度L/D的增加,筋材与土体的相互作用面增大,其二者间摩擦和嵌咬作用增强,故加筋效果越来越好。

图6 加载后的格栅变形Fig.6 Deformation of geogrid after loading
2.2 筋材埋深对加筋防护效果的影响
针对单层筋材加筋,选取管道埋深H/D=2、筋材长度L/D=4,对比筋材埋深u/D分别为0.5、1.0和1.5时的加筋效果。图7给出了不同筋材埋深下P-Hb/D和Pr/Pu-Hb/D关系曲线。由图可知,不同筋材埋深u/D对应的侵入荷载P均持续增长,但P-Hb/D曲线的拐点位置和变化幅度有所不同;此外,当Hb均为15 cm(约1.4D)时,u/D由0.5增加至1.0,Pr增加了11.8%,而u/D由1.0增加至1.5,Pr减小了23.5%。
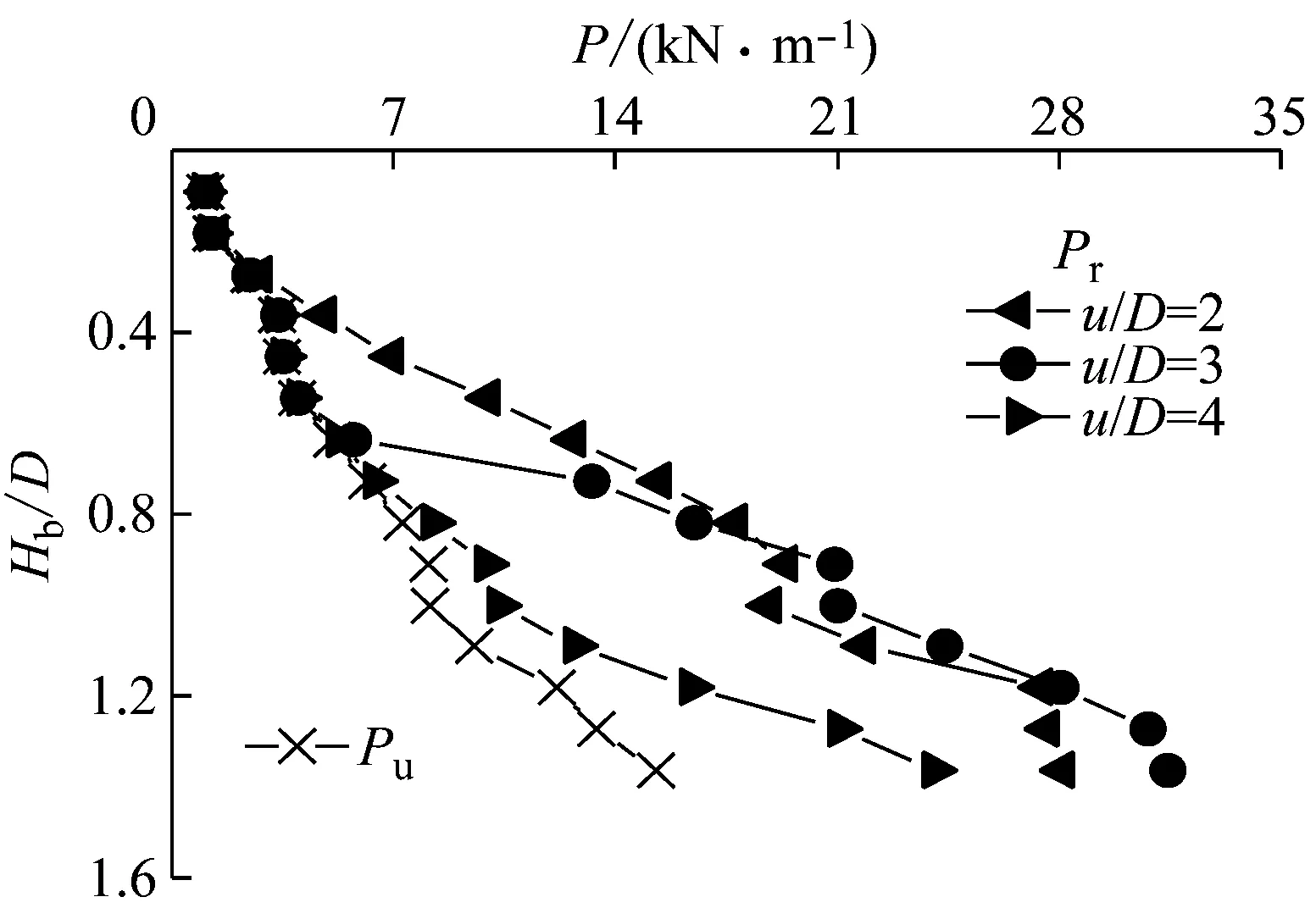
(a) P Vs Hb/D

(b) Pr/Pu Vs Hb/D图7 不同筋材埋深下侵入荷载随侵入深度的变化
Fig.7 Variation of the intrusive load with intrusive depth under different depths of reinforcements
究其原因,当u/D=0.5时,由于筋材埋深小,筋材对侵入体阻碍作用力Fr在侵入深度Hb较小时便有了明显的体现,所以P-Hb/D曲线较早出现拐点,但筋材上覆土层厚度过薄导致筋材与土体间的相互作用(摩擦和嵌咬作用)较弱,因此加载后期P和Pr/Pu值相对较小;当u/D=1.0时,筋材埋深增大,且筋土间相互作用增强,使得筋材对侵入体的阻挡作用显著提高;当u/D=1.5时,由筋材埋深过大,侵入体始终未到达筋材所在位置,筋材没有对其产生直接的阻挡,加筋作用未能充分发挥,从而造成其加筋效果与u/D=1.0时比略显逊色。
2.3 筋材间距对加筋防护效果的影响
在多层筋材防护模式基础上,选取管道埋深H=2D、筋材长度L=4D和筋材层数n=2,首层筋材埋深u/D=0.5,对比筋材间距s/D分别为0.5和1.0时的加筋防护效果。
图8给出了不同筋材间距下的P-Hb/D和Pr/Pu-Hb/D关系曲线。由图可知,增加筋材层数可明显提高侵入荷载,且侵入深度Hb/D相等时,筋材间距s/D=0.5时的Pr和Pr/Pu值均比s/D=1.0时大。其中,当s/D=0.5时,Pr/Pu整体上为先增大后减小的变化趋势,其最大值(Pr/Pu)max位于2层筋材的中间位置附近(即Hb=u+s/2处附近);当s/D=1.0时,Pr/Pu随Hb/D的增加波动较大,其最大值(Pr/Pu)max出现在靠近底层筋材处。
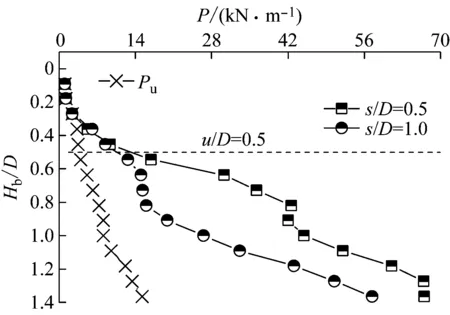
(a) P Vs Hb/D
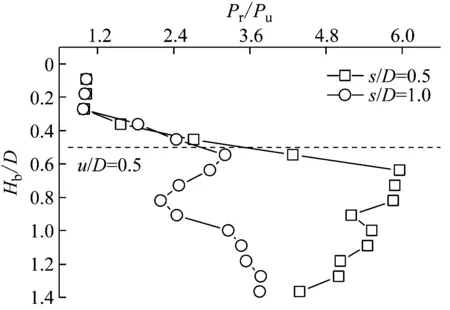
(b) Pr/Pu Vs Hb/D图8 不同筋材间距下侵入荷载随侵入深度的变化
Fig.8 Variation of the intrusive load with intrusive depth under different spacing of reinforcements
其原因在于:当s/D=0.5时,筋材间距较小,筋材对土体的侧向约束作用较强,且侵入过程中侵入体与上层筋材接触作用不久后又受到下层筋材的约束,上下层筋材协同作用良好,使侵入荷载得到很好地扩散,因此加筋效果显著;而当s/D=1.0时,侵入体最终侵入深度未抵达下一层筋材,因此下层筋材作用未能有效发挥,使得其整体加筋效果要比s/D=0.5时稍差。结合图7对比分析可知,同等条件下,筋材层数越多,P和Pr/Pu值越大,表明增加筋材层数可使加筋效果更显著。
2.4 管道径向变形
在管道埋深H/D=2和筋材长度L/D=4的前提下,根据图3中所示的不同加筋模式选取以下4种工况:
(1)n=0;
(2)n=1,u/D=0.5;
(3)n=2,u/D=0.5,s/D=0.5;
(4)n=2,u/D=0.5,s/D=1.0。
对比分析钢板侵入体贯入时侵入荷载P与管道径向变形比U/D(即管道径向变形U与管道外径D之比)的关系,如图9所示。

图9 不同加筋模式下的管道径向变形比Fig.9 Radial deformation ratio of pipes under different reinforcement modes
由图可知,随着Hb/D的增大,侵入荷载P和管道变形比U/D显著增加,其中管道水平方向径向扩张,垂直方向径向收缩,由于左右两侧受到土体约束,管道水平径向变形比Uh/D始终小于垂直径向变形比Uv/D;当侵入荷载相同时(如P=15和30 kN/m),筋材层数越多,管道变形比越小,表明增加筋材层数可以有效提高土体强度,在管道上方形成保护层,但随着侵入荷载的持续增加,荷载作用效果越来越大,管道变形逐渐达到规范限值5%D[15-16]。
2.5 管周环向应变
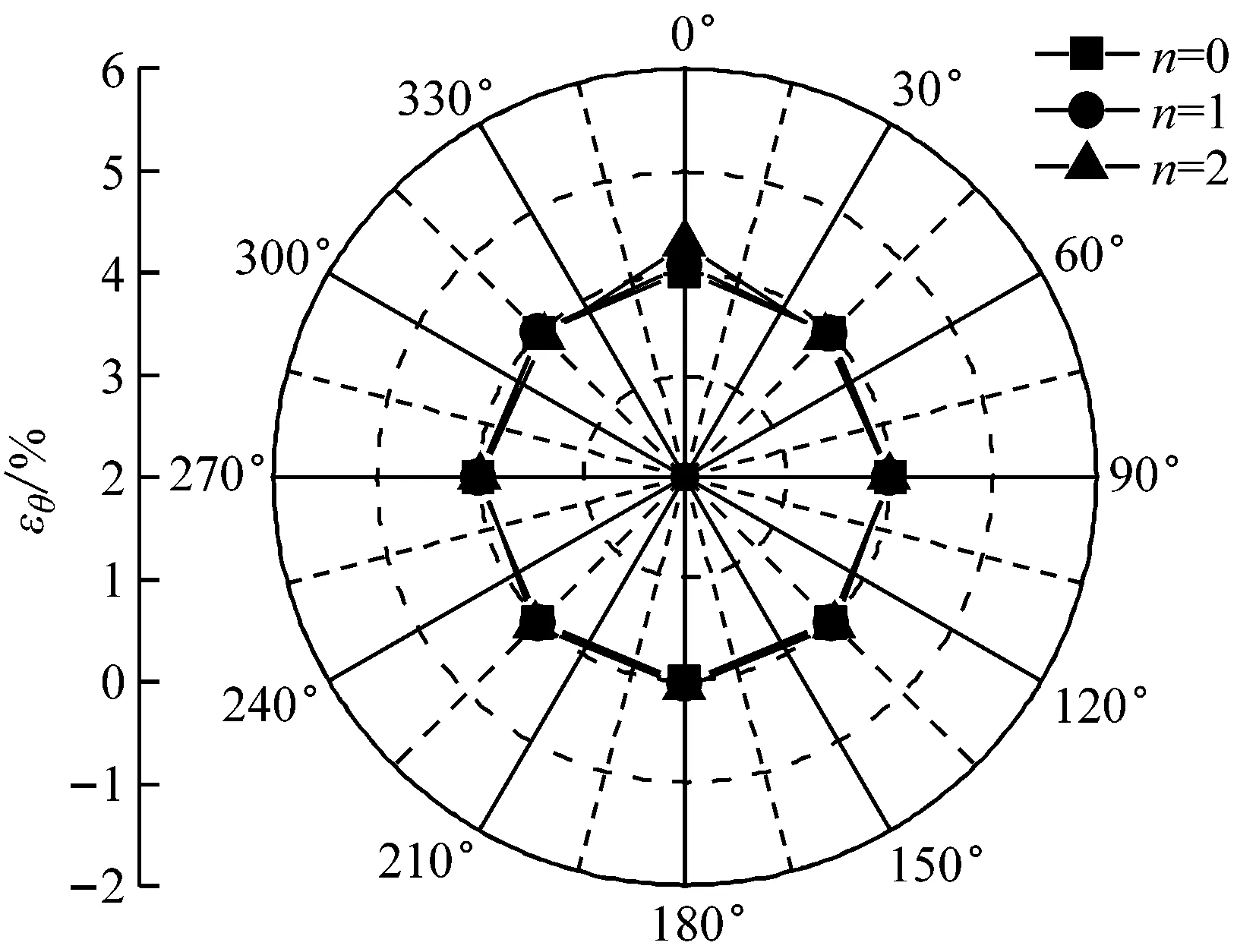
基于H/D=2、L/D=4、u/D=0.5和s/D=0.5,对比筋材层数分别为n=0、1和2时管道应变的变化和分布规律。图10给出了试验过程中侵入深度Hb/D分
(a) Hb/D=0.6

(b) Hb/D=0.8
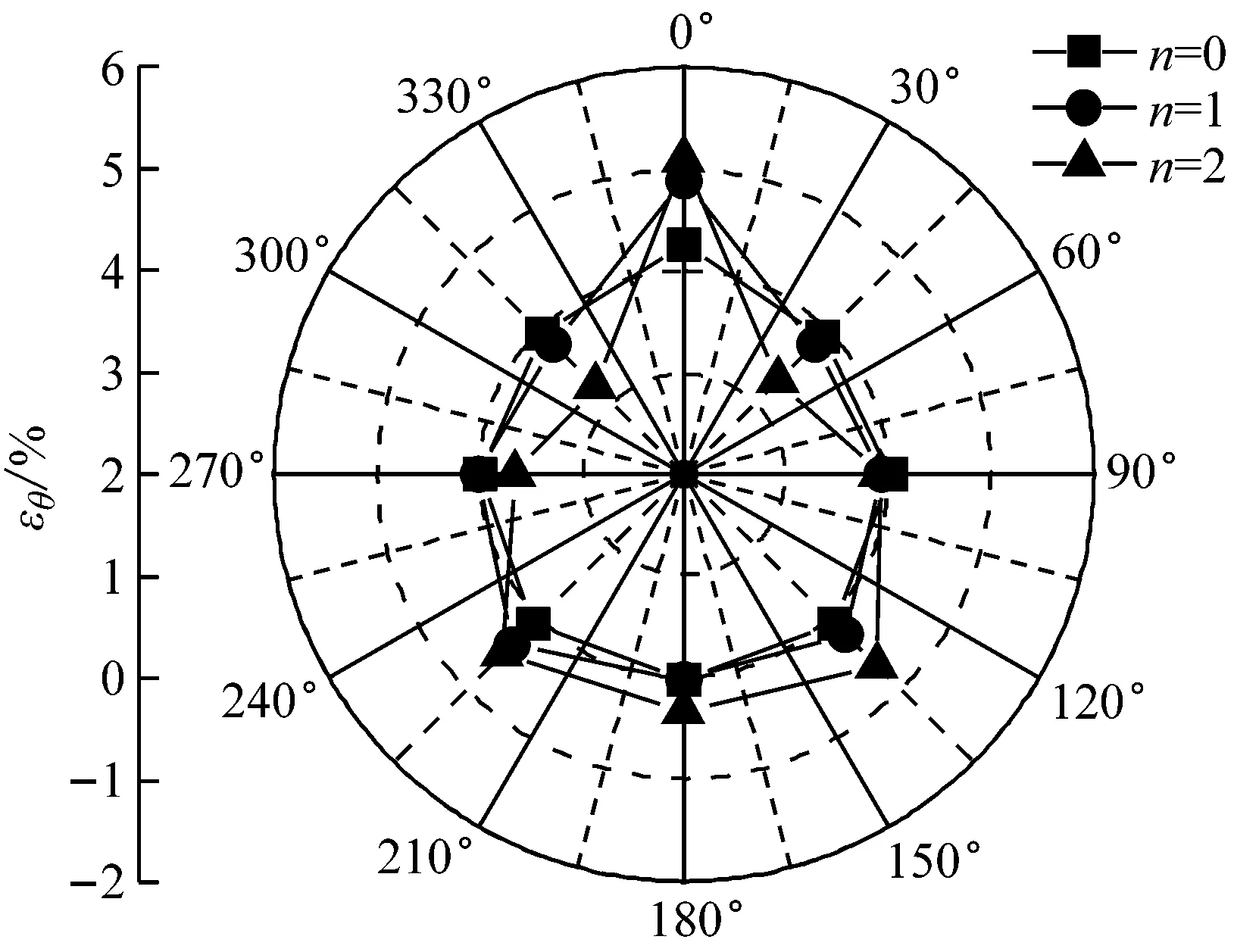
(c) Hb/D=1.0
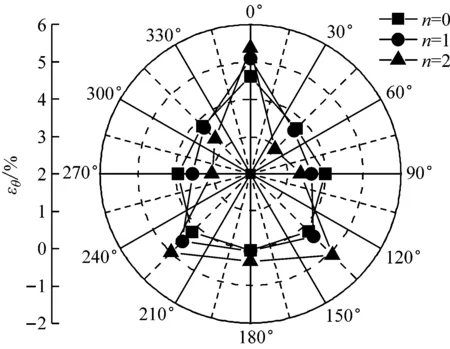
(d) Hb/D=1.2图10 加载过程中不同加筋层数下的管周环向应变Fig.10 Circumferential strains of pipes under different layers of reinforcement during loading
别为0.6、0.8、1.0和1.2时不同加筋层数下的管周环向应变εθ。由图可知,随着钢板侵入深度Hb的增加,管周各点的应变越来越显著;且在相同的侵入深度Hb下,管周应变随着加筋层数n的增加而增大。其主要原因是:筋材层数越多,加筋层间土体的强度越高,同时其传递荷载的性能越好,达到相同侵入深度所需施加荷载明显增加。因此,加筋层对管道产生的荷载作用效果也就越显著。
另外,观察管道环向应变εθ的分布形式可以发现,由于侵入体贯入时将土体向两侧挤压,造成管道两肩附近(30°~90°、270°~330°)受到的压力显著,因此该范围内应变值小于0,为受压,而在管顶(0°)和管底附近(135°~225°)的应变值大于0,为受拉。
3 结 论
(1) 机械侵入荷载作用下,采用土工格栅加筋防护埋地管道效果显著,其中在侵入体与格栅接触初期,即Hb=u时,加筋效果最为突出,随后筋材在土体间发生滑动,加筋效果减弱。
(2) 同等条件下,Hb=15 cm(约1.4D)时,L/D由3增至4,P增加了9.01%;u/D由0.5增至1.0,P增加了11.8%,表明增加筋材长度或埋深后侵入荷载明显增加,加筋效果更为显著;筋材间距较小时,上下层筋材协同抵抗侵入荷载的作用良好,加筋效果明显。埋地管道的径向变形随侵入荷载的增加而增大,且垂直方向径向变形始终大于水平方向;同级荷载作用下,增多加筋层数,管道径向变形显著减少。
(3) 侵入体从埋地管道正上方贯入时其两侧挤土效应显著,管道应变随侵入深度的增加而增大,其分布规律为管道两肩附近(30°~90°、270°~330°)受压,管顶(0°)和管底附近(135°~225°)受拉。
