双激振电机驱动旋转振动筛系统的同步理论研究
2019-04-22侯勇俊谭海军吴先进
侯勇俊, 谭海军, 方 潘, 吴先进, 蒋 瑞
(1.西南石油大学 机械工程学院, 成都 610500;2.四川宝石机械专用车有限公司,四川 广汉 613800)
在自然界和日常生活中同步现象随处可见,振动系统的自同步是指系统依靠自身较弱的耦合特性调节子系统的频率使其达到协调统一[1]。对于同步现象的研究最早可以追溯到1673年惠更斯(Huygens)对于耦合单摆实验同步现象的观测。近年来同步现象的研究主要包括化学、物理和社会等领域,例如混沌同步系统,耦合旋转振动筛系统。振动机械的自同步理论最早是由俄罗斯Blekhman等[1]提出。在国内Hou等[2]利用Lyapunov稳定性理论研究了双轴二倍频振动筛的稳定性及自同步,并实现了二倍频的自同步稳定运转。Wen等[3]采用小参数平均法计算出了系统的稳定性及自同步,并通过实验验证了其理论的正确性。Zhao等[4]采用改进小参数法推导出了平面运动双质体振动系统中两偏心转子的无量纲耦合方程,并依据其零解的存在及稳定性计算出了多激振电机系统的稳定性及自同步。Jiang等[5]用哈密顿原理近似表达了旋转振动筛的动力学方程并研究了其非线性振动理论。Li等[6]由偏心转子无量纲耦合方程零解存在条件得到了振动机实现自同步运动条件,并根Routh-Hu rwitz判据得到振动机同步运行的稳定性条件。Fang等[7-9]采用庞加莱法研究系统同步性和稳定准则,并通过中心流形定理判断其稳定性条件。近年来,对于振动系统的自同步理论研究的学者越来越多,但是大多只是涉及平面振动系统的自同步理论[10-13],对于空间振动系统的自同步理论研究较少。平面振动系统的运动轨迹一般为直线、圆和椭圆,其运动形式单一限制了其使用范围。对于旋转振动筛系统,其运动方式为多自由度的空间运动,广泛应用于医药、制盐、磨料磨具、铸造、矿业、建材、食品化工、轻工、木材造纸、制糖、粮食加工和化肥等许多行业[14]。
旋转振动筛通过改变系统的相关参数调整同步相位差可以实现水平面的摇动、垂直方向的运动以及切向的运动,3种运动形式经过不同组合, 可以实现物料在筛面的均匀分布、 合理抛跳的螺旋向外三维空间复杂运动,有效地利用了全部圆形筛面,提高了筛分效率[15];有效解决了细粒级物料的干法和湿法筛分透筛困难问题。通过偏心、径向偏角和切向偏角的合理调节可以实现预定的各种运动模式适合于许多行业不同物料的有效筛分[16]。
1 理论和模型
1.1 基本理论
假设旋转振动筛系统动力学方程为
(1)
(2)
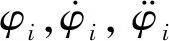
在系统进入自同步状态以后,转子的角速度为ω,在一个周期内,忽略小参数项的影响(μ=0),则振动系统做强迫稳态振动响应为
x=x(ωt,α1,α2…αk)
(3)
假设转子的初相位为α1,α2,…,αk,那么转子的实际相位角可以表示为:
φi=ωt+αi
(4)
假设上式中参数α1,α2,…,αk分别对应一个值满足方程
(5)

(6)
如果参数α1,α2,…,αk的一组常数满足(7)且代数方程
(7)
如果χ的根实部为负,那么在μ足够小的情况下α1,α2,…,αk的值是唯一的,这时方程(7)就存在稳定解;如果χ的根实部为正,则解不稳定;如果χ至少有一个根实部为零,则其稳定性可以用中心流形定理判断[1]。
1.2 力学模型
双激振电机驱动旋转振动筛系统的力学模型如图1所示,旋转振动筛系统以系统质心为坐标原点建立动坐标系,以系统静止时质心所在位置建立定坐标系。该系统由质量为m0(kg)的振动体和两个质量分别为m1,m2(kg)的偏心块构成。两激振电机质心与系统质心位于平面xoz,振动体和机架之间用刚性弹簧连接,弹簧在x,y,z,ψ1,ψ2方向的刚度系数分别为kx,ky,kz,kψ1,kψ2(N/m),阻尼系数分别为fx,fy,fz,fψ1,fψ2(N·s/m)。激振电机固定在振动体上,偏心块质心到回转中心的距离为r(m),两激振电机安装中心到振动体质心之间的距离分别为l1,l2(m),激振电机安装角分别为β1,β2(rad)。转子1和转子2的相位角分别为φ1,φ2(rad),偏心块安装角为ε(rad)。
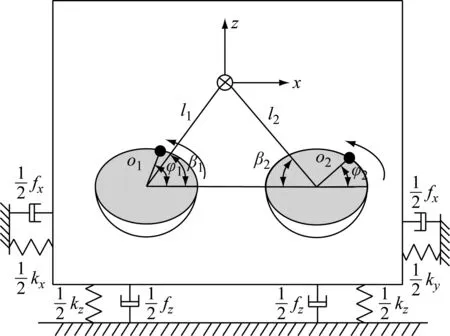
图1 旋转振动筛系统力学模型Fig.1 Mechanics model of rotary vibrating screen system
该系统的总动能为
(8)
式中:J1,J2是偏心转子的转动惯量;J11,J22分别是振动体沿着y和z轴旋转的转动惯量;ψ1,ψ2分别是振动体沿着xoz平面和xoy轴旋转的角位移。fx,fy,fz分别是系统在x,y,z平动方向的阻尼系数,fψ1,fψ2分别是系统在ψ1,ψ2转动方向的阻尼系数。
旋转振动筛系统的总势能为
(9)
旋转振动筛系统的总耗能为
(10)
将式(8),(9),(10)代入拉格朗日方程
(11)

(12)
2 稳定性和同步性
2.1 系统稳态近似解
当系统达到稳定状态后,其在各个方向的阻尼对系统的响应的影响可以忽略。在其系统动力学方程中引入小参数μ,并忽略其中小量对系统的影响,将动力学方程(12)改写为
(13)
由前面基本理论可知
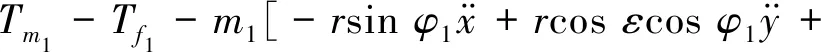
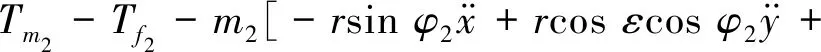

(14)
(15)
其中
(16)
由方程(13)可以得到旋转振动筛系统是关于自由度x,y,z,ψ1,ψ2的耦合动力学方程,因此方程中包含小参数的项可以被忽略并引入无量纲参数:
(17)
其中ωx,ωy,ωz,ωψ1,ωψ2为系统的频率系数,是弹簧刚度和系统总质量的函数。其中λx,λy,λz,λψ1,λψ2为频率比系数,是激振电机频率和频率系数的函数,直接将弹簧刚度、系统质量和激振电机频率联系在一起。从式(18)可以得到引入无量纲参数后极大程度上简化了方程式(15)的形式,直接将系统的相关参数用无量纲参数替代,这样就更形象的反应了旋转振动筛系统的有关特点。把无量纲参数代入到式(16)
A1=A2=-rmrλx,B1=B2=-rmrλy,
C1=C2=-rmrλz
D1=D2=-re1rl1λψ1,D3=D4=-re2rl2λψ2,
D5=-re1rl1λψ1,D6=-re2rl2λψ2
(18)
则式(15)可以写为
(19)
2.2 系统自同步性
当振动系统达到稳定状态后,转子的角速度逐渐趋近一个稳定值ω;假设偏心转子1和2的初相位分别为α1,α2,则偏心转子在某一时刻t其相位为
φ1=ωt+α1,φ2=ωt+α2,α=α1-α2
在一个周期T内对式(14)积分,由等式(6)可以得到

B2ω2m1rcos2εsinα-C2ω2m1rsin2εsinα-
D3ω2m1rl1sin2εcosβ1cosβ2sinα-
D4ω2m1rl1sinεsinβ2cosβ1cosα-
D3ω2m1rl1sinεsinβ1cosβ2cosα+
D4ω2m1rl1sinβ1sinβ2sinα-
D6ω2m1rl1sinεcosεsinα,
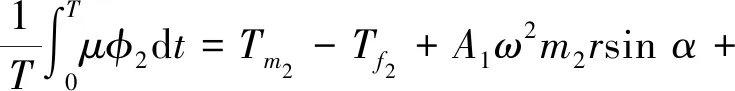
B2ω2m2rcos2εsinα+C1ω2m2rsin2εsinα+
D1ω2m2rl2sin2εcosβ1cosβ2sinα-
D2ω2m2rl2sinεsinβ2cosβ1cosα-
D1ω2m2rl2sinεsinβ1cosβ2cosα-
D2ω2m2rl2sinβ1sinβ2sinα+
D5ω2m2rl2sinεcosεsinα
(20)
式中:Lmi为感应第i个激振电机的互感系数;Lsi为第i个激振电机的定子电感;rm为激振电机的极对数;ωm为自同步电角速度;Rri为第i个激振电机的转子电阻;US0为定子电压的幅值[7]。
整理式(20),由前面基本理论可以得到系统的平衡方程为
μ1sinα+μ2sinα+μ3cosα=0
(21)
其中
μ1=4rmλx
μ2=l1l2(re1λψ1+re2λψ2)(sin2εcosβ1cosβ2-
sinβ1sinβ2+sinεcosε)
μ3=l1l2(re2λψ2-re1λψ1)sinεsin(β1+β2)
由等式(7)可以得到系统的稳定性条件为
(22)
把式(20)代入式(22),系统自同步稳定性准则可简化为
μ1cosα+μ2cosα-μ3sinα<0
(23)
由式(21)可知,系统的同步稳定准则主要由偏心块安装角、弹簧刚度、激振电机安装位置和系统质量决定。只有当这些参数满足振动方程和稳定准则时,两偏心转子才可以实现同步运转。根据(21)可以得到,当偏心块水平安装的时候,系统达到平衡后其转子相位差为0。当激振电机安装在质心所在水平面附近的时候,系统达到平衡后其转子相位差在0的附近波动。
3 数值模拟
3.1 系统自同步数值分析
为了验证上述结论的正确性,按照表1所给出模型的参数,在MATLAB中进行系统自同步数值分析,其相应仿真参数如表1。由式(21)可知,系统同步稳定准则主要由偏心块安装角、弹簧刚度、激振电机安装位置和系统质量决定。只有当这些参数满足振动方程和稳定准则时,两偏心转子才可以实现同步运行。为了更加准确的描述系统的自同步过程,采用单一控制变量原则,分别讨论弹簧刚k和偏心块安装角ε对系统自同步过程的影响。

表1 系统仿真参数Tab.1 System emulation parameters
合理选择系统参数不仅可以正确描述旋转振动筛系统的运动轨迹,更能精准的反应系统的同步行为。表1给出了系统的部分参数,图2(a)是当l1等于l2为0.3(m),kψ1=kψ2=105(N/m),kx=ky=kz=105(N/m),两激振电机到系统质心连线与水平面夹角β1,β2相等,且β1分别为0°,30°,45°时候偏心块安装角ε与系统同步行为之间的关系。图2(b)是当l1=0.3(m),kψ1=kψ2=105(N/m),kx=ky=kz=105(N/m),两激振电机中心位置到系统质心连线与水平面夹角β1,β2不等(两激振电机质心始终处于同一水平面),使β1=45°保持不变,β2分别为0°,30°,45°的时候偏心块安装角ε与系统同步行为之间的关系。
从图2(a)可以得到当两激振电机连线与系统质心处于同一水平面的时候,偏心块安装角ε无论如何变化两偏心转子的相位差始终为0,此时系统在偏心块安装角ε所在的方向做轨迹为圆的运动。当两激振电机连线与系统质心不在于同一水平面的时候,两偏心转子的相位差随着安装角ε的增大而增大。因此,改变安装角ε就可以使旋转振动筛系统按照预定的方式运动。从图2(b)我们可以得到,在同一水平面改变激振电机的安装角β2可以使两偏心转子的相位差α=|α1-α2|的大小发生变化。当增大β2时两偏心转子的相位差α随之增大,此时系统在空间中的运动轨迹也随之发生变化。因此可以通过改变偏心块安装方向或者改变激振电机安装位置去调节振动筛的在空间中的运动轨迹。
图3(a)是当l1等于l2为0.3(m),kx=ky=kz=105(N/m),偏心块安装角ε=45°,两激振电机中心位置到系统质心连线与水平面夹角β1,β2相等分别为0°,45°,60°的时候弹簧扭转刚度与系统同步行为之间的关系。图3(b)是当l1等于l2为0.3(m),kx=ky=kz=105(N/m),偏心块安装角ε=90°,两激振电机中心位置到系统质心连线与水平面夹角β1,β2相等分别为0°,45°,60°的时候弹簧扭转刚度与系统同步行为之间的关系。
从图3(a)和(b)可以得到当激振电机安装角β1等于β2为0时候,改变弹簧刚度两偏心转子的相位差α保持不变。当kψ1
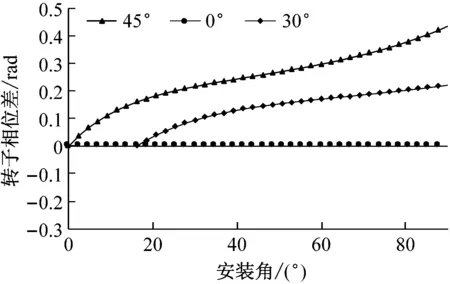
(a) β1=β2分别为0°,30°,45°

(b) β1为45°且β2分别为0°,30°,45°图2 偏心块安装角ε与转子相位差之间的关系
Fig.2 The relationship between installation angleεand system self-synchronization
3.2 自同步运动状态
选取表1中的参数,其中弹簧刚度kx=ky=kz=kψ1=kψ2=105(N/m),偏心块安装角ε=45°,l1=l2=0.3 m,激振电机安装角β1等于β2为45°时候。选取激振电机1和激振电机2为鼠笼式三相异步激振电机,其转速为1 440 r/min,频率为50 Hz,功率为3.8 kW。其仿真参数如图4,从图4(e)可知当系统达到稳定后两激振电机的角速度在155 rad/s左右波动,这与其额定转速基本相近。从图4(a),(b),(c)中可以看出系统在2 s左右达到稳定状态,其在x,y,z方向的振幅分别为2.1、1.3、1.3 mm。由前面的结论可知当弹簧扭转刚度kψ1=kψ2的时候两偏心转子的相位差α=0,此时系
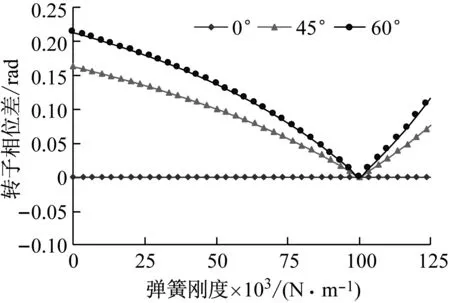
(a) 偏心块安装角ε=45°

(b) 偏心块安装角ε=90°图3 弹簧刚度k与转子相位差之间的关系Fig.3 The relationship between the spring stiffness k and the system self-synchronization
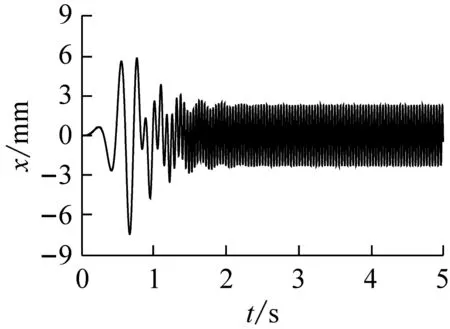
(a) x方向的位移

(b) y方向的位移

(c) z方向的位移

(d) 电磁扭矩

(e) 转子转速图4 旋转振动筛数值仿真结果Fig.4 Numerical simulation results of rotating vibrating screen
统沿着与水平面夹角为ε的平面方向做轨迹为圆的空间运动。从图1可以得到系统在x,y,z方向做周期运动,其在空间中的合成运动刚好与结论符合。
选取表1中的参数,其中弹簧刚度kx=ky=kz=kψ1=kψ2=105N/m,偏心块安装角ε=15°,l1=l2=0.3 m,激振电机安装角β1=β2=45°时候。选取激振电机1和激振电机2为鼠笼式异步电动机,其转速为1 440 r/min,电动机频率为50 Hz,功率为3.8 kW。其仿真参数如图5,从图5(a),(g),(h)可以得到当偏心块安装角ε=15°的时候,系统在1.9 s左右达到稳定状态,其在x,y,z方向的振幅分别为2.2、2.1、0.5 mm,这时旋转振动筛系统主要在水平面内运动。随着偏心块安装角的增大其在z方向的位移增大,因此调节偏心块安装角就可以调节旋转振动筛系统在空间中的运动轨迹,从而满足实际生产需求。

(a) x方向的位移
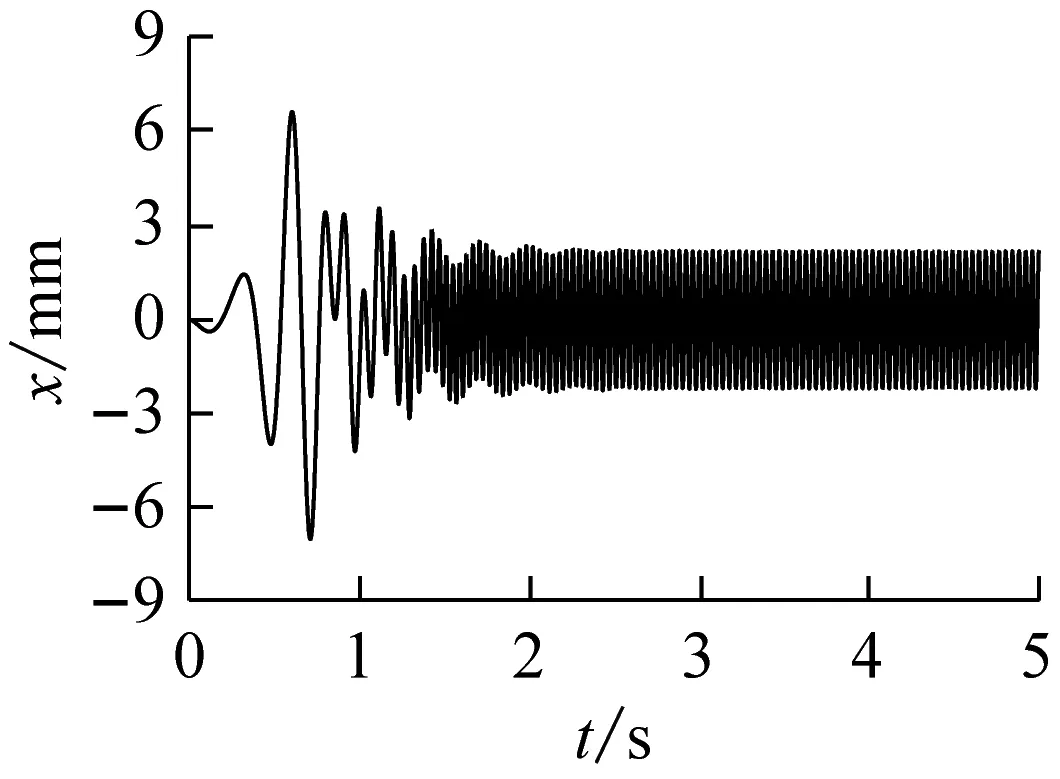
(b) y方向的位移

(c) z方向的位移图5 旋转振动筛数值仿真结果Fig.5 Numerical simulation results of rotating vibrating screen
4 结 论
本文研究了一种旋转振动筛系统的稳定性和同步性,首先利用拉格朗日方程建立了旋转振动筛系统的空间运动的动力学方程,然后将动力学方程转化为无量纲方程,利用拉普拉斯变换对该方程求解,得到了系统的自同步条件和稳定准则。最后通过MATLAB进行数值仿真验证了其理论的正确性。得到了以下结论:
(1) 系统的平衡方程为μ1sinα+μ2sinα+μ3cosα=0,系统的稳定性准则为μ1cosα+μ2cosα-μ3sinα<0
(2) 通过拉格朗日方程得到了旋转振动筛系统在x,y,z方向的运动规律。旋转振动筛系统其独特的空间运动形式可以完善传统平面振动的缺点,使平面振动过渡到空间振动。
(3) 当偏心块安装角ε为0 rad或者激振电机安装角β1,β2分别为0 rad时两偏心转子的相位差为0,此时系统在x,y,z方向的分运动均达到稳定状态。
(4) 本文通过理论分析得到了系统的同步和稳定条件,当β1=β2时系统更容易达到稳定状态。当增大偏心块安装角ε时,两转子相位差也随之增大。最后采用数值模拟的方式验证了其理论的正确性。
