基于最优型确定性测量矩阵的振动信号数据压缩采集方法

郭俊锋， 党姜婷

(兰州理工大学 机电工程学院，兰州 730050)

机械振动信号承载并传递着机械设备运转过程中的多样化信息，实时检测并提取振动过程中的有用信息，对机械设备的故障信息判定和生产维护尤为重要。传统的且目前被广泛采用的振动信号采集都是以奈奎斯特采样理论为指导的模数(A/D)采样，它指出采样频率不低于原始信号最高频率的两倍，才能精确重建出该信号。然而，如今的机械设备日趋高速化和大型化，振动频率越来越高且呈现非线性、非平稳性的特点。如果依然用传统的采样定理进行采样，必然要求更高的采样频率，同时产生海量的监测数据，这些数据的实时传输、同步存储与后期处理已成为亟待解决的工程技术瓶颈问题[1]。

近年来出现的压缩感知理论[2](Compressed Sensing，CS)对上述问题的解决起到了启示作用，该理论指出，如果原信号是稀疏的或在某种变换域下可压缩，就能以远低于奈奎斯特的速率对信号采样的同时进行压缩。压缩感知主要由信号的获取和重建两大部分构成，作为压缩感知最核心内容的测量矩阵在这两部分中都起着重要作用：测量矩阵性能越好，需要的采样数越少，重建误差也越小。目前的测量矩阵主要分为随机性矩阵和确定性矩阵两大类。在压缩感知理论初期，以高斯矩阵[3]为代表的随机性测量矩阵，因其所需测量数目少、重构精度高而备受青睐，但其结构复杂，占用的存储空间大，随机变元多，不利用硬件实现。相反，确定性测量矩阵结构简单，大大降低了硬件构造难度，有利于工程实现，因此，国内外许多学者转而研究了确定性矩阵，如Toeplitz矩阵[4]、循环测量矩阵等，但因确定性测量矩阵的重建误差较大，未能得到广泛应用。

在测量矩阵的优化方面，大量研究表明，增大测量矩阵和稀疏表示矩阵的非相干性，可以提高压缩感知的整体效率[5]。学者们提出不同的算法来降低测量矩阵和稀疏表示矩阵之间的相干系数，如Elad[6]算法，Abolghasemi等[7]的梯度下降算法，Duarte-Carvajalino等[8]算法，及Xu等[9]的角紧框架训练算法等。此外，Donoho提出的测量矩阵需要满足的三个特征表明：测量矩阵优化的另一个出发点是提高测量矩阵自身列向量的独立性。如QR分解算法、SVD算法等。然而，上述两大类优化方法都只是单方面提高测量矩阵的性能，未能使压缩感知达到最优效果。目前也有学者针对特定信号，研究出了不同的测量矩阵，比如，基于雷达图像的卷积测量矩阵[10]、基于信道的时域测量矩阵[11]等，然而，鲜有研究针对机械振动信号的测量矩阵。

针对上述测量矩阵存在的问题，本文从工程应用角度出发，得益于文献[12]的启示，以机械振动信号为研究对象，设计出适用于机械振动信号的最优型确定性测量矩阵，进而提出一种基于最优型确定性矩阵的振动信号数据压缩采集方法。考虑对确定性矩阵的典型代表——Toeplitz矩阵，进行正交化及对称化，减少独立变元，构造出易于硬件实现的OST矩阵。为了提高OST矩阵的重构精度，从非相干性出发，将上述两大类优化方法结合起来，首先根据最优测量理论，通过阈值迭代收缩算法优化OST测量矩阵，以降低OST测量矩阵与稀疏基之间的互相干性，其次采用SVD算法，进一步提高OST矩阵自身列向量独立性，最终得到适用于振动信号的最优型确定性测量矩阵。本文提出的振动信号压缩采集算法运行速度快，在提高测量矩阵压缩性能的同时大大降低了计算复杂度。

1 压缩感知基本理论

压缩感知理论指出：倘若一个信号本身是稀疏的或者在某种变换域下是可压缩的，那么通过一个与稀疏变换基不相关的测量矩阵，就可以将原始信号从高维空间投影到低维空间，从而得到一组远小于原始信号长度的测量值，并且通过重建算法，可以由这些少量的测量值重建出原始信号。压缩感知基本模型如下：

(1)

式中：f为原始信号，f∈Rn；α为f在稀疏变换基Ψ下的稀疏系数(α中非零值的数目K远远小于信号的长度N)；y为观测值，y∈Rm×1；Φ为m×n的观测矩阵；D(D=ΦΨ)为m×n的感知矩阵。其中，Φ必须满足下述约束等距性质(RIP)：

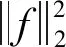
(2)

式中：0<δk<1，f为一稀疏向量。由式(1)反求f的过程为信号的重建过程，重建过程一般通过求解l0范数问题来实现，但因为l0范数问题是一个NP-hard难题，因而转为求解等价的l1范数问题，求解这类问题的典型算法主要有以基追踪为代表的凸优化算法，和以正交匹配追踪[13](Orthogonal Matching Pursuit，OMP)为代表的贪婪迭代算法等。

对于构造的测量矩阵，只有其以高概率满足RIP特性，才可以从少量的测量值y中精确地重建出原始信号，然而，要证明其满足RIP是很复杂的，因此，常常采用与RIP等价的非相干特性作为测量矩阵构造与优化的参考依据。

2 基于最优型确定性测量矩阵压缩采集振动信号数据的整体方案

将压缩感知理论应用于振动信号数据的采集过程，其前提条件是该振动信号是可压缩的或稀疏的，因此，首先应分析振动信号的稀疏特性，之后再设计振动信号数据压缩采集的整体方案。

2.1 机械振动信号的稀疏性分析

信号是稀疏的或可压缩的分两种情况，其一，信号本身是稀疏的或可压缩的；其二，信号在某种变换下是稀疏的或可压缩的。大部分实际信号(包括本文研究的机械振动信号)都属于第二种情况。常用的稀疏变换基有：离散余弦变换基(DCT)、小波基(DWT)及傅里叶变换基(DFT)等，本文研究机械振动信号在DCT正交基下的稀疏特性，同时估计其稀疏度K。随机地从美国西储大学轴承数据库中选取512个数据开展振动信号的稀疏性研究。图1为振动信号的时域波形，图2为该振动信号在DCT基下的变换系数按绝对值从大到小排列后的系数分布。

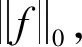
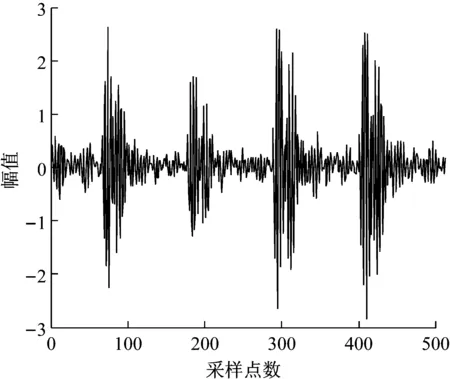
图1 振动信号时域波形Fig.1 Time-domain waveform of the vibration signal

2.2 基于最优型确定性测量矩阵压缩采集振动信号数据的整体框架

为了在不丢失原始振动信息的情况下，提高机械振动信号数据压缩采集的效率，提出一种基于最优型确定性测量矩阵的振动信号数据压缩采集方法，其框图如图3所示，该方法以振动信号的稀疏性为先验，其测量过程为：首先分析信号在DCT基上的稀疏性，结合稀疏度K构造最优型OST确定性测量矩阵，然后按照公式(1)的CS基本模型压缩采集振动信号得到压缩测量值y，最后将y通过数据传输网络输送到信号重构与检测环节，一方面可直接通过携带振动信号全局信息的压缩值y进行信息提取，完成状态检测，另一方面，可选用经典的OMP算法，融入振动信号的稀疏信息，用少量的压缩值y重构出原始信号进行检测，并计算重构精度。本文在提出该方法的基础上，重点研究振动信号压缩采集环节中最优型确定性测量矩阵的设计。

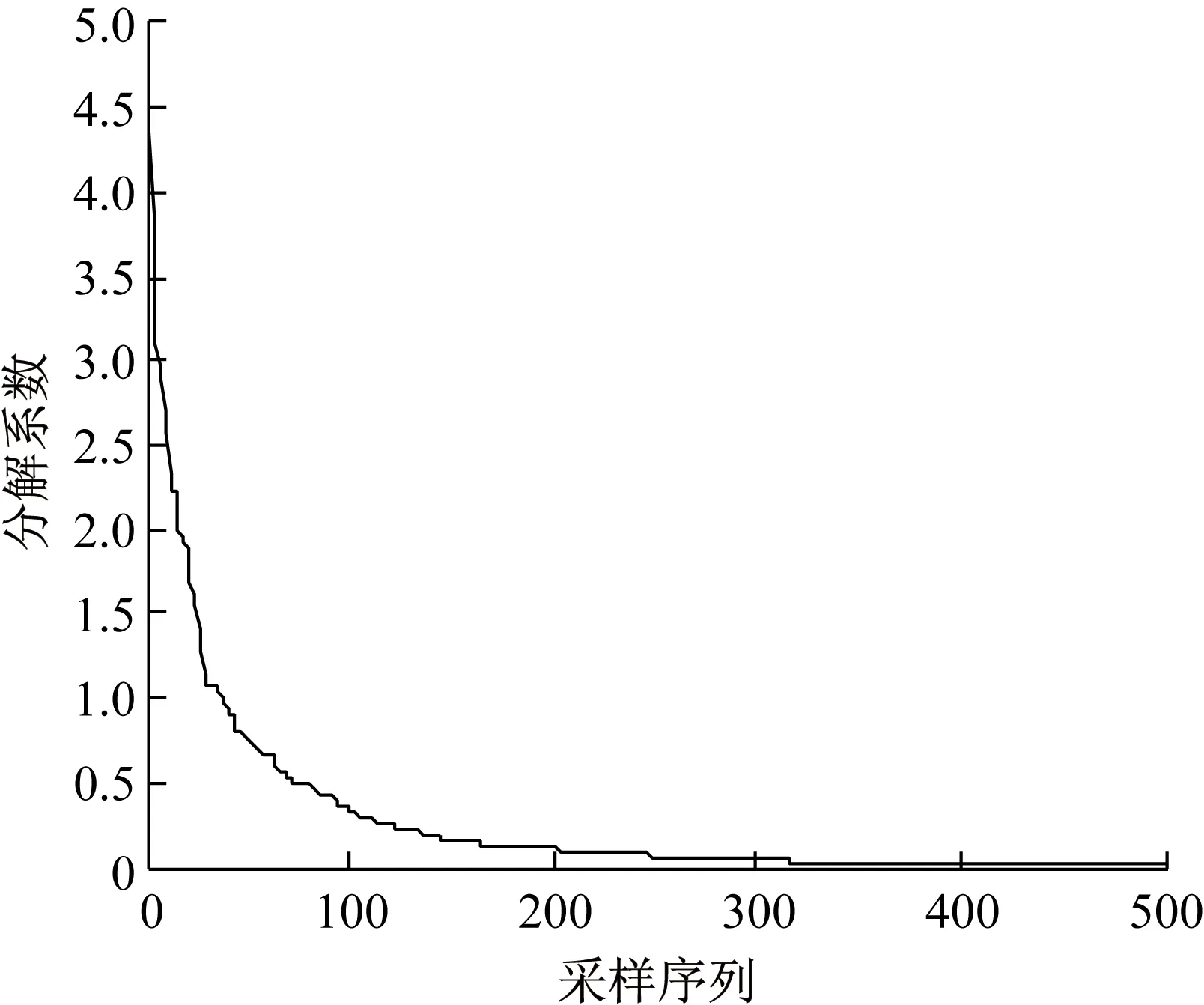
图2 振动信号在DCT基下的变换系数衰减分布

Fig.2 The change coefficient attenuation distribution of the vibration signal under DCT base

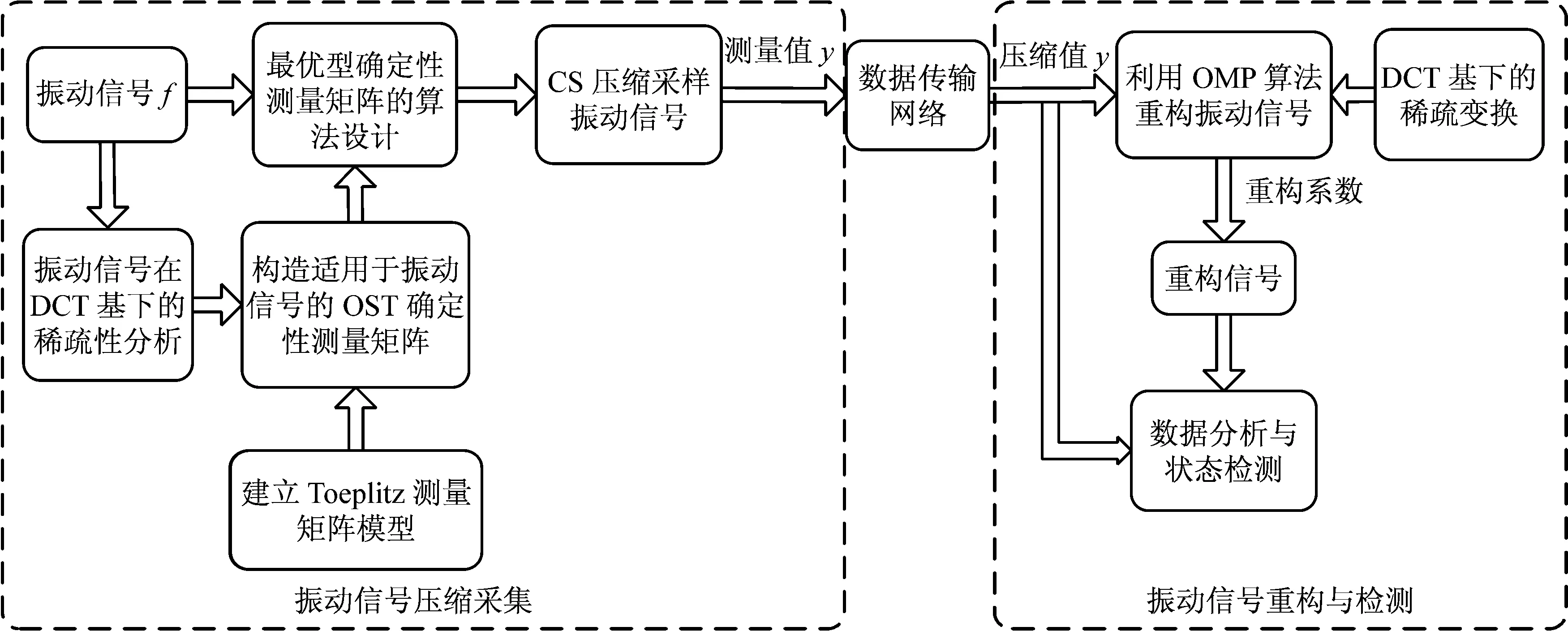
图3 基于最优型确定性测量矩阵的振动信号数据压缩采集方法框图Fig.3 A block diagram of the data compression method for collecting vibration signals based on optimal deterministic measurement matrix

3 最优型确定性测量矩阵的设计

3.1 确定性测量矩阵模型

以Toeplitz测量矩阵为基础，对其进行改进，建立OST确定性矩阵模型。

Toeplitz测量矩阵的形式如下：

(3)

该矩阵由元素取值为±1的随机行向量通过循环移位得到一个方阵，并对其列向量进行标准的归一化处理得到，存储量极少，但因其元素取值单一，导致矩阵的非相干性较小，因此重建误差较大。

国内外众多学者对Toeplitz测量矩阵做出了改进：Bottcher[15]提出了一种新型的确定性观测矩阵——正交对称托普利兹(OST)矩阵；Li等[16]证明，如果一个矩阵满足统计约束等距性(Statistical Restricted Isometry Property，SRIP)，也可以作为压缩感知的观测矩阵；Li等又证明，OST测量矩阵满足SRIP，并且其感知性能与随机性矩阵相当。受此启发，考虑将OST矩阵应用于振动信号的压缩采集过程中，并验证其压缩性能。

OST测量矩阵的模型如下：

(4)

该矩阵由特定的随机序列通过循环移位得到一个方阵，并随机选取其中的M行之后标准化得到：首先定义符号序列σ(σ1,σ2,…,σN)，OST矩阵的首行元素由该序列通过逆傅里叶变换得到，即按式(5)生成：

(5)

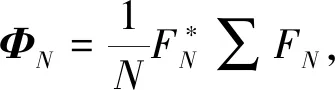
3.2 最优型确定性测量矩阵的设计

如前所述，目前测量矩阵的优化一般从非相干性出发，考虑两方面：一是增大稀疏基和观测矩阵之间的非相干性，二是降低测量矩阵本身的列相干性。本文将用于降低测量矩阵和稀疏基相关性的阈值迭代法和用于增加测量矩阵自身列独立性的SVD算法相融合，层层优化OST矩阵，得到适用于振动信号的最优型确定性测量矩阵。

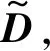
(6)

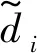
(7)

则基于该矩阵，此时互相干系数μ可定义为：

(8)

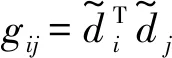
(9)

此时优化的目标是降低观测矩阵Φ和稀疏基Ψ的t-平均互相关系数μt(D)，以得到改进的矩阵Φ′。

相比原始OST矩阵，经上述阈值迭代算法改进后的Φ′，重构性能有了一定程度的提高，但还未达到最佳的感知效果，即此时得到的矩阵并非是最优的，因此，下一步将采用SVD算法继续优化Φ′。

测量矩阵经SVD分解后可以增大矩阵的最小奇异值，该值越大，测量矩阵的列向量独立性越强，该矩阵用于信号压缩感知时的性能也就越强。SVD算法的主要思想为：将测量矩阵Φ′作对角化分解得Φ′=UΛPT，其中U∈RM×M和P∈RN×N均是正交阵，Λ∈RM×N是对角阵，Λ的对角线上的元素是测量矩阵Φ′的奇异值。现对Λ做限定：只保留Λ正对角线上绝对值前M大的因子，其余都设为0，即

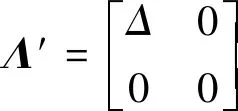
(10)

式中：Δ=diag(σ1,σ2,…,σM)，优化后得到测量矩阵Φ″=UΛ′PT。

基于阈值迭代收缩与SVD联合优化算法的最优型OST矩阵设计方案为：

输入参数：相干性阈值t，尺度下降因子γ(0<γ<1)，最高迭代次数Itermax，迭代的次数(q=1:Itermax)，测量数M，稀疏基ΨDCT，测量矩阵Φ，感知矩阵D=ΨDCTΦ。

具体步骤如下：

步骤1 对Φ进行列单位化，获得初始矩阵Φ0

步骤2 根据振动信号在DCT基下的稀疏特性，确定Φ0的行数，即测量数M

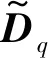
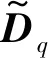
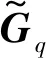
(11)

步骤9 用SVD算法优化Φ′，得到测量矩阵Φ″

输出：稀疏基ΨDCT对应的最优型OST矩阵Φ″

其流程图如图4所示。

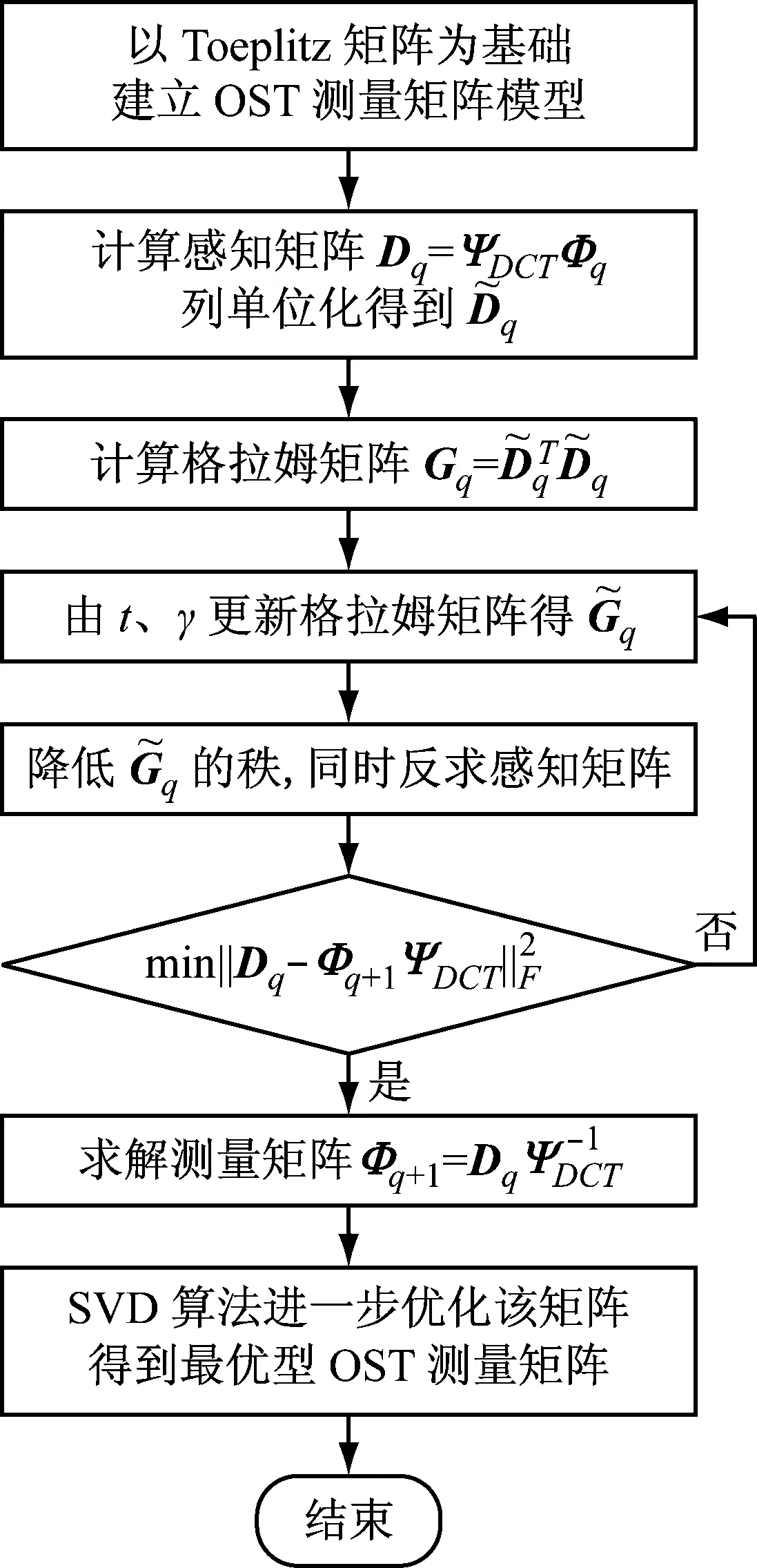
图4 最优型OST测量矩阵的构造流程图Fig.4 Constructed flow chart of the optimal OST measurement matrix

上述测量矩阵的设计过程中，首先以振动信号的稀疏性为先验信息，通过构造感知矩阵D得到格拉姆矩阵，然后通过阈值迭代更新格拉姆矩阵，反求出感知矩阵，以得到改进的矩阵Φ′，最后再采用SVD算法提高Φ′的列独立性，得到适用于振动信号的联合优化下的最优型确定性OST测量矩阵Φ″。

4 基于最优型确定性测量矩阵压缩测量振动信号的数据采集方法实现步骤

步骤1 提取振动信号数据，对该振动信号在DCT正交基下进行稀疏性分析，获得其先验信息及稀疏度K。

步骤2 根据振动信号的稀疏性等先验信息，以Toeplitz矩阵为基础，建立易于硬件实现的确定性OST测量矩阵模型。

步骤3 针对OST测量矩阵重建精度不高这一问题，采用不同算法层层优化该矩阵，设计适用于振动信号的最优型OST矩阵Φ″。

步骤4 以Φ″为测量矩阵，利用y=Φf，对振动信号f进行压缩测量，将N维振动信号在测量矩阵上投影为M维的测量值y。

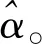
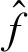
步骤8 采用在重构误差最小的情况下得到的最优型Φ″压缩测量振动信号，从而得到少量的测量值y，进行振动信号数据分析与状态检测。

基于最优型OST测量矩阵的机械振动信号数据压缩采集方法流程图，如图5所示。

5 实验与分析

为验证提出的基于最优型确定性测量矩阵的机械振动信号数据压缩采集方法的有效性，选用美国西储大学轴承数据库中的数据做试验验证。试验对象是轴承型号为6025-2RS JEM SKF的深沟球轴承，在轴承外圈6点钟方向设置故障，其形式为电火花加工生产的单点故障，其直径是0.178 cm，轴承负载是0，传感器安装在轴承驱动端，信号采样频率是12 000 Hz。首先采用DCT正交基对信号进行稀疏表示，之后压缩测量，恢复算法采用OMP算法。实验中将最优型OST测量矩阵应用于机械振动信号的压缩测量中，观察其压缩性能，对比矩阵有高斯矩阵、Toeplitz矩阵、OST测量矩阵、OST-阈值迭代优化矩阵及OST-SVD优化矩阵。

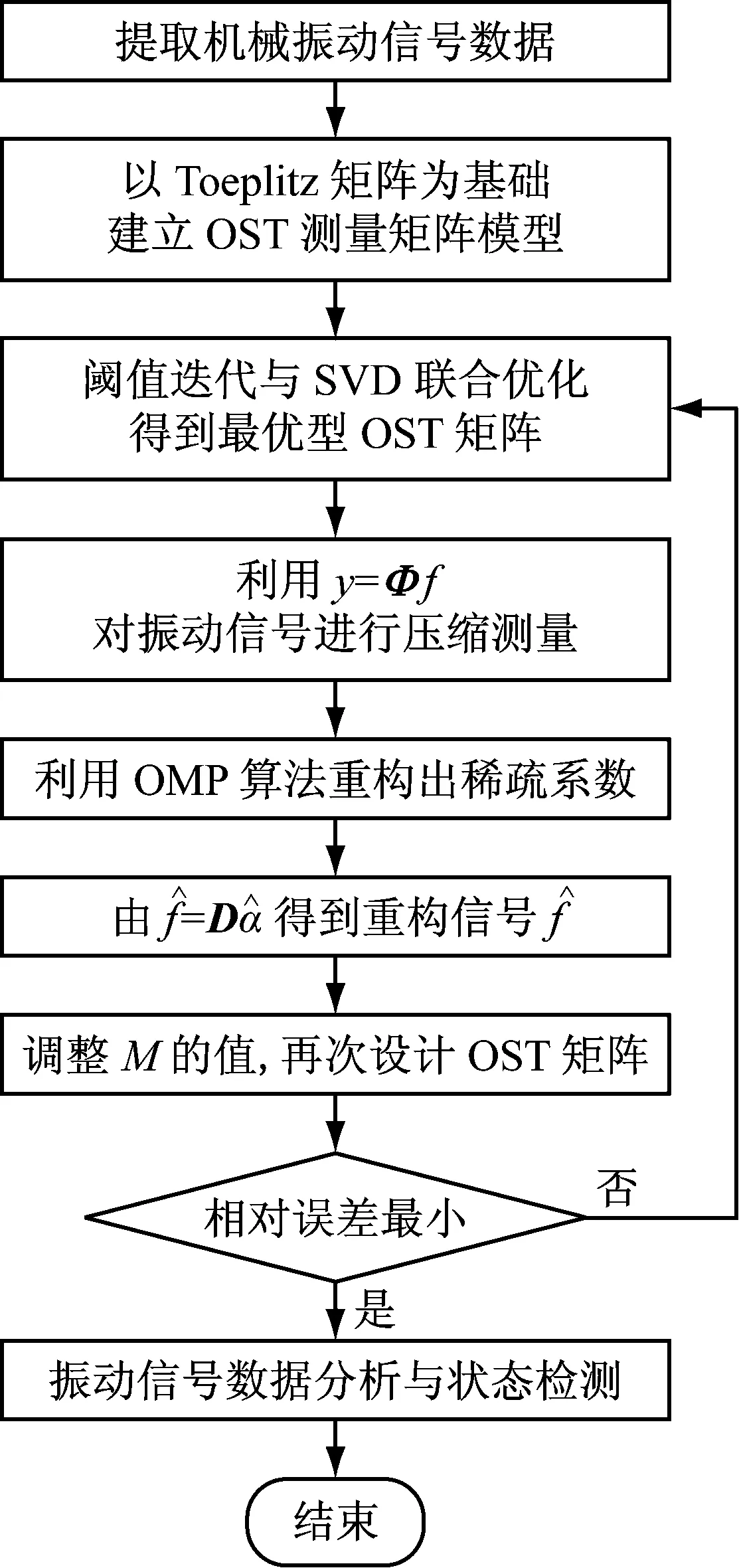
图5 基于最优型OST测量矩阵的振动信号数据 压缩采集方法流程图

Fig.5 A flow chart of the data compression acquisition method of vibration signal based on optimal deterministic matrix

本文分别采用压缩率CR、相对误差δ、匹配度β等指标来衡量振动信号的压缩性能。

(1)压缩率(Compression Rate，CR)，衡量振动信号的压缩程度。CR越大，表示压缩程度越大，所需要的测量数越少，其定义为

(12)

式中：n是原始振动信号的长度；m是压缩测量振动信号的长度。为了精确重构振动信号，压缩测量数m必须满足式(13)

(13)

式中：常数c≈0.28；k为稀疏度。由前面分析可知，当振动信号n的长度为512时，k=137，计算得m≥51，由上面两式联立得CR≤90%，即压缩感知时压缩率不能太大，否则测量数目过少，达不到精确重构原始振动信号的效果，同时压缩率也不能过小，否则测量数过多，达不到压缩的效果，因此压缩率的范围限定为60%≤CR≤85%。

(2)相对误差(Relative Error)，衡量振动信号的重构性能，是指振动信号的绝对误差与原始信号的比值，其定义为

(14)

(3)匹配度(Matching Degree)，衡量振动信号的重构性能，是指重建信号与原始信号的相似程度，其计算公式为：

(15)

式中：β表示匹配度，β∈[0,1]，其值越大，重建匹配度越高，表明压缩性能越好。

所有的实验数据均在双核、8 G运行内存的台式机的MATLAB R2014a软件下运行，所有的实验结果均是运行100次取平均值得到的。

5.1 确定性OST测量矩阵应用于振动信号的压缩性能分析

(1)压缩率固定时，确定性OST矩阵的性能分析

选取长度n=512的振动信号数据，稀疏度K=137，依上述分析，测量数取为80～200，即压缩率的变换范围为85%～60%，可较为准确地重构出原始振动信号。首先固定压缩率为75%，即测量数固定为128时，比较原始振动信号和高斯矩阵、Toeplitz矩阵、OST测量矩阵重构的振动信号波形图，实验结果如图6所示。

图6表明：在压缩率固定为75%时，从直观上可以看出，相比Toeplitz矩阵，同样作为确定性测量矩阵的OST测量矩阵可以更精确地重建原始信号，也可以看出OST测量矩阵相比高斯矩阵重建的信号更加接近于原始振动信号。表1为固定压缩率为75%时，三种不同测量矩阵下振动信号的重构误差、匹配度、矩阵构造时间和占用内存的性能指标比较。

表1表明：高斯矩阵随机性强，重建误差较小，但其运行时间和占用内存较大；Toeplitz矩阵结构简单，所占用的内存较小、运行时间较短，但重构误差很大；OST矩阵为Toeplitz矩阵的变形，复杂度和Toeplitz矩阵相当，都比较小，但因其正交对称的性质，重构误差有所降低，略优于高斯矩阵。

(2)压缩率变化时，确定性OST矩阵的性能分析

图7给出不同测量矩阵的重建误差随着压缩率的变化曲线，即当测量值在60～270范围内变化时，不同测量矩阵下机械振动信号的重建误差。图8给出不同测量矩阵的波形匹配度随压缩率的变化曲线，即不同测量矩阵下重构振动信号与原始振动信号的相似程度比较。

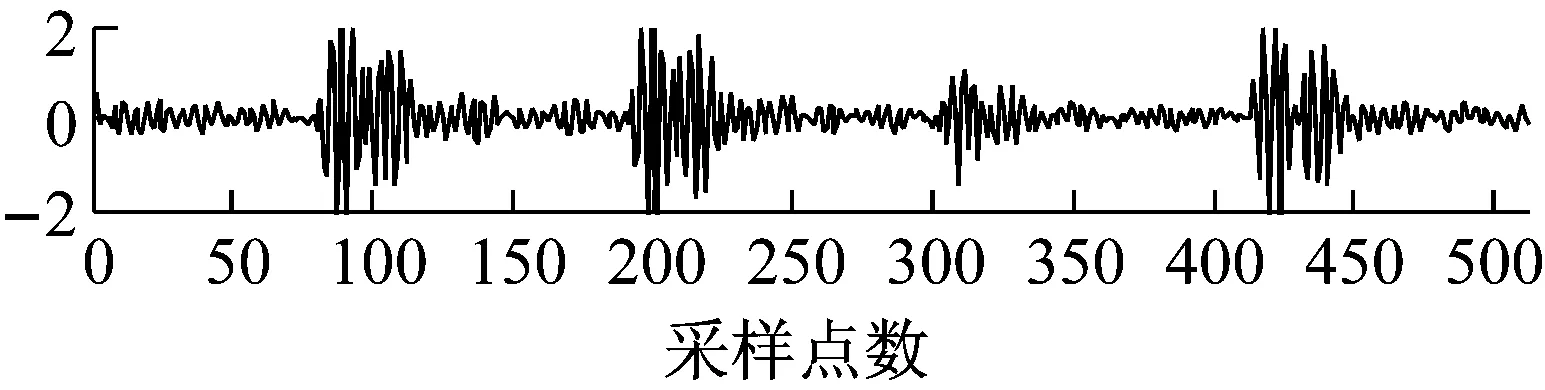
(a) 原始振动信号

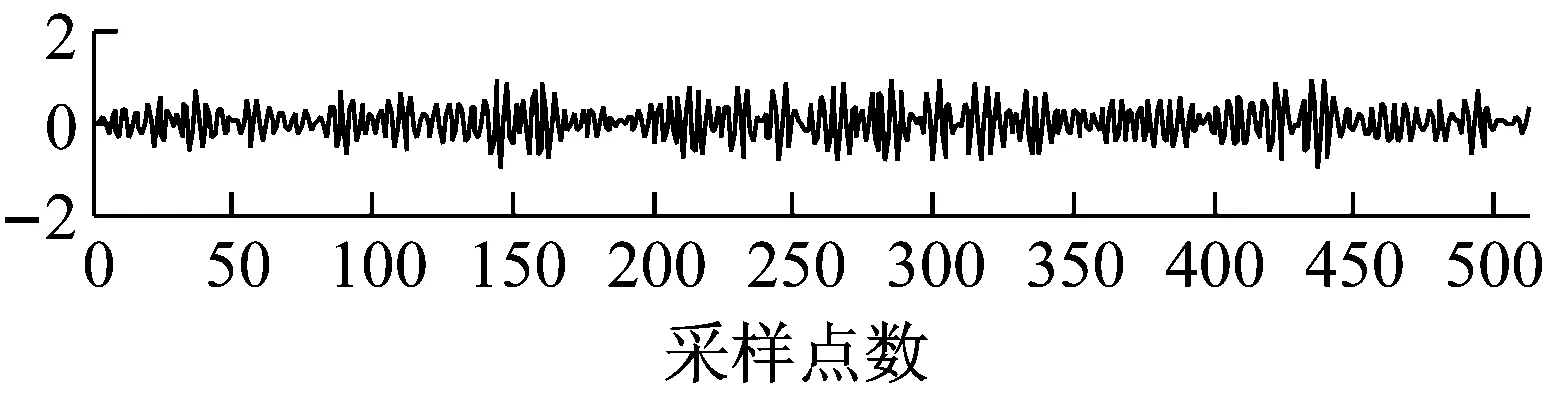
(b) Toeplitz矩阵

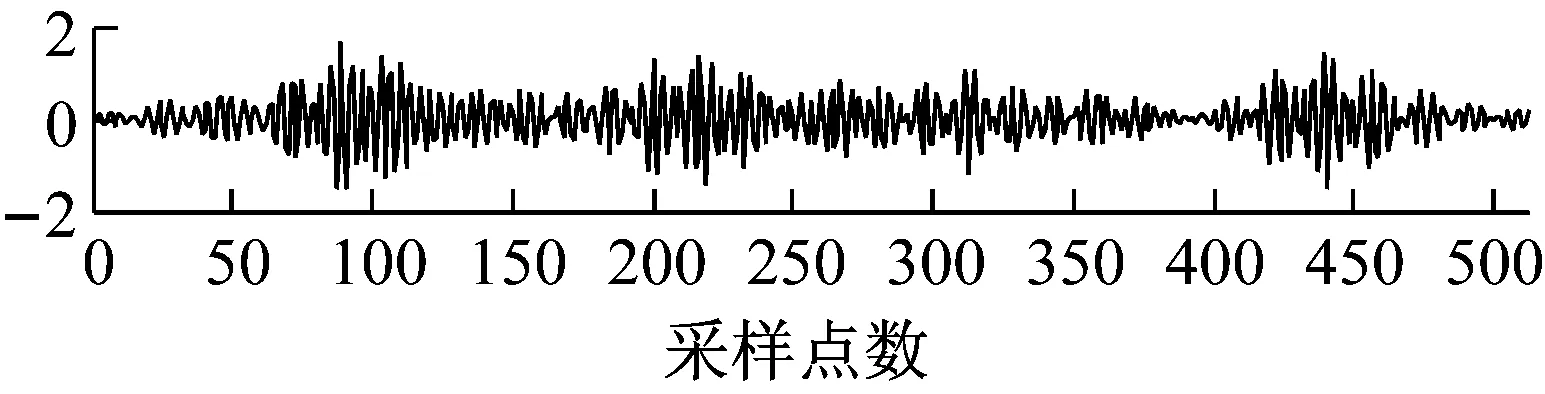
(c) 高斯矩阵

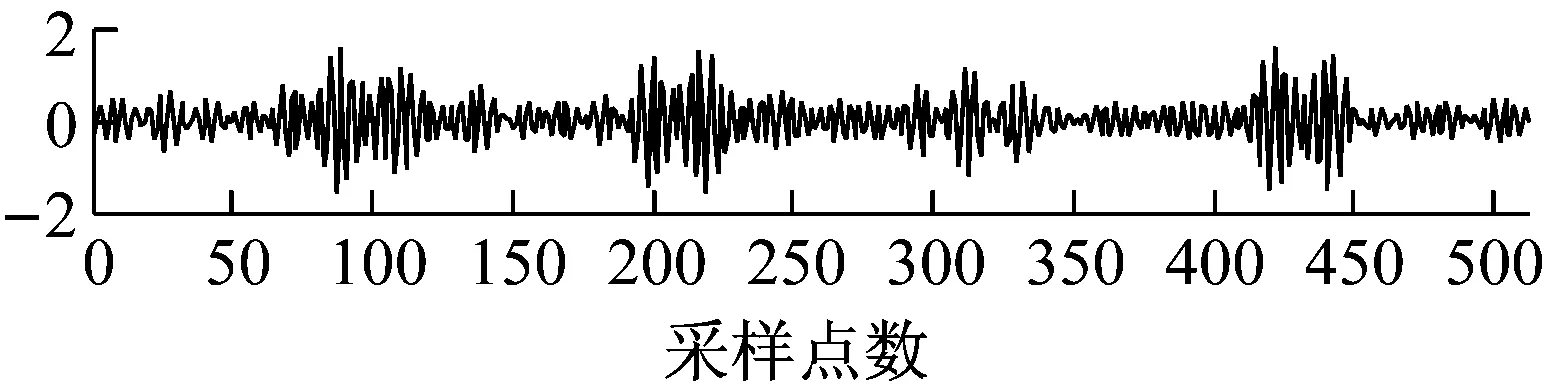
(d) OST矩阵图6 CR为75%， 不同矩阵重建振动信号与原始振动 信号对比图

Fig.6 A comparison diagram of the reconstructed vibration signals under different matrices with the original vibration signal when the CR is 75%

表1压缩率为75%，不同测量矩阵的重构性能比较

Tab.1Thecomparisonofdifferentmatrices’reconstructionperformancewhentheCRis75%

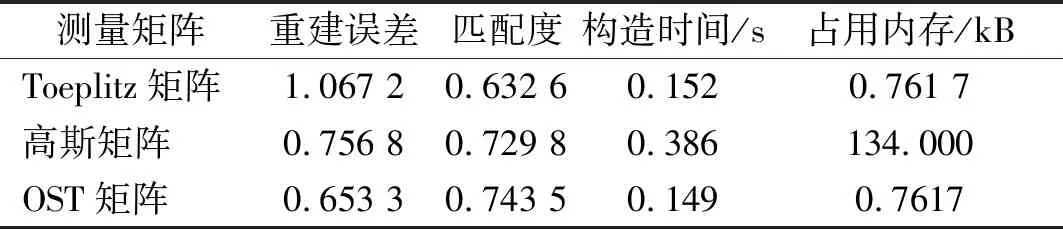
测量矩阵重建误差匹配度构造时间/s占用内存/kBToeplitz矩阵1.067 20.632 60.1520.761 7高斯矩阵0.756 80.729 80.386134.000OST矩阵0.653 30.743 50.1490.7617

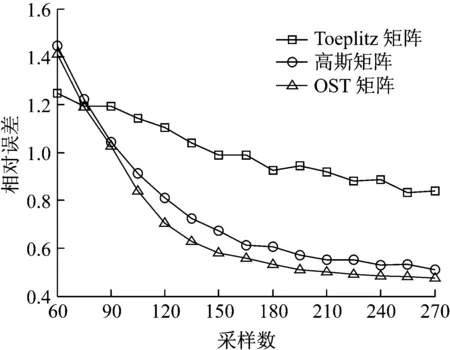
图7 三种不同矩阵下振动信号的重建误差Fig.7 The reconstruction error of vibration signal under three different matrices

图7表明：当测量数大于80，即压缩率小于86%时，随着测量数的不断增大，各矩阵下振动信号的重建误差都不断减少。其中，Toeplitz矩阵的重建误差最大，高斯矩阵的重建误差次之，OST矩阵的重建误差最小。同时，通过图8也可以看出，Toeplitz矩阵重建的振动信号波形匹配度最小，无论采样数如何变化，其匹配度在60%左右，基本没提高，可以看出Toeplitz矩阵作为测量矩阵的局限性，相比之下，OST测量矩阵重建的原始振动信号波形匹配度较好。

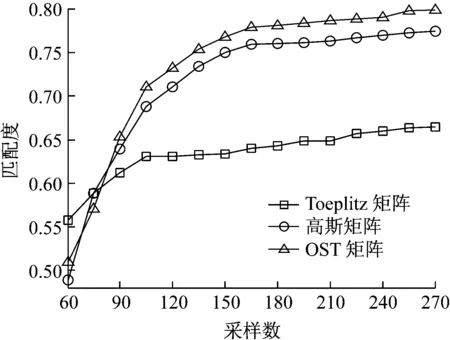
图8 三种不同矩阵下重建振动信号的波形匹配度

Fig.8 The degree of waveform matching of the reconstructed vibration signals under three different matrices

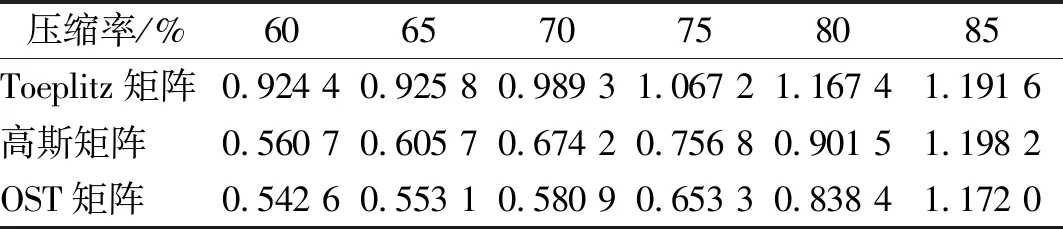
表2 不同矩阵的相对误差值Tab.2 Relative errors under different matrices

表2表明：随着压缩率的不断增大，各矩阵的重建误差值也在增大，相比之下，OST测量矩阵的误差最小，说明OST测量矩阵应用于振动信号压缩测量的感知性能优于高斯矩阵和Toeplitz矩阵，但从误差的具体数值来看，OST矩阵的压缩测量性能仍有很大的提升空间，因此，下一步实验将分别采用阈值迭代法和SVD算法对OST矩阵进行优化，并对比优化前后振动信号的重构性能。

5.2 最优型确定性OST测量矩阵应用于振动信号的压缩性能分析

5.2.1 压缩率固定时，最优型OST矩阵的性能分析

针对OST测量矩阵应用于振动信号仍然没有达到最优的压缩效果这一问题，采用不同的优化算法对OST矩阵进行优化。图9为固定压缩率为75%时，OST测量矩阵、OST-阈值迭代优化矩阵、OST-SVD优化矩阵、最优型 OST测量矩阵重构的振动信号与原始振动信号比较图。

图9表明：相比于OST测量矩阵，优化以后的OST矩阵能够更精确地重建原始振动信号，直观上说明，最优型OST测量矩阵重建的信号与原始振动信号差异最小，几乎可以完美重构。表3为固定压缩率为75%，OST矩阵及不同优化算法下的OST矩阵的压缩性能比较。

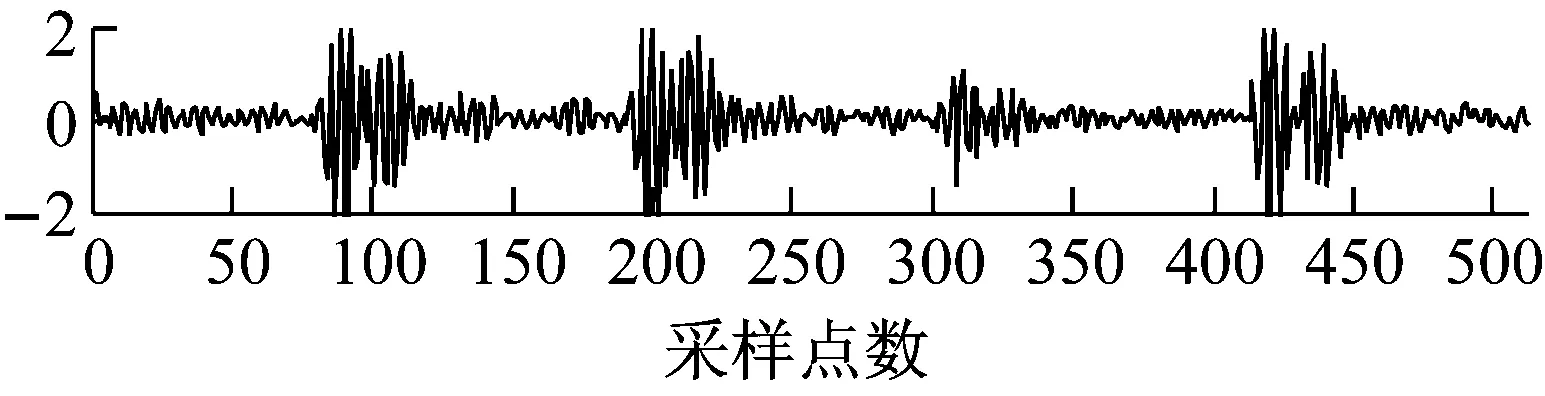
(a) 原始振动信号

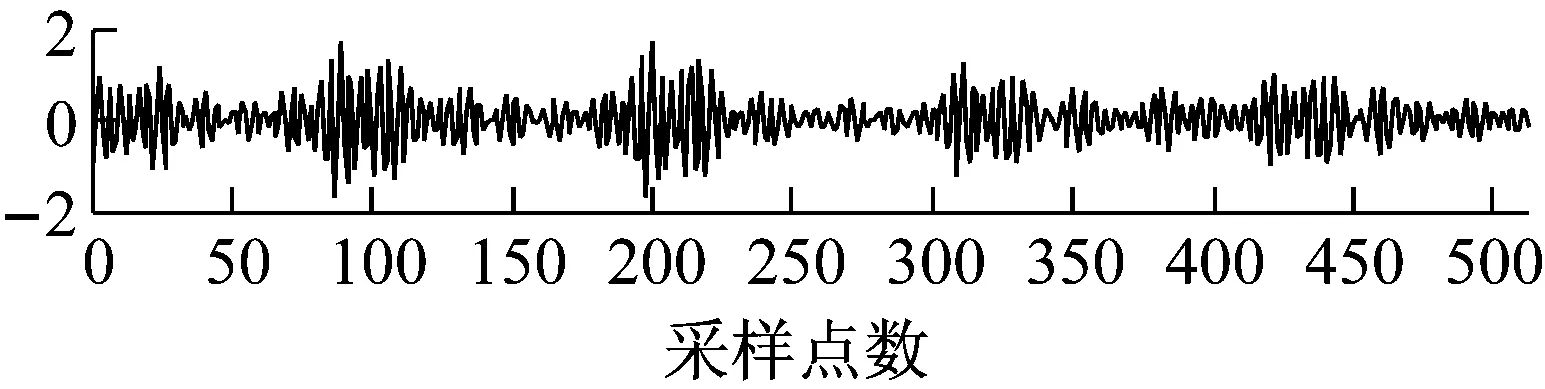
(b) OST矩阵

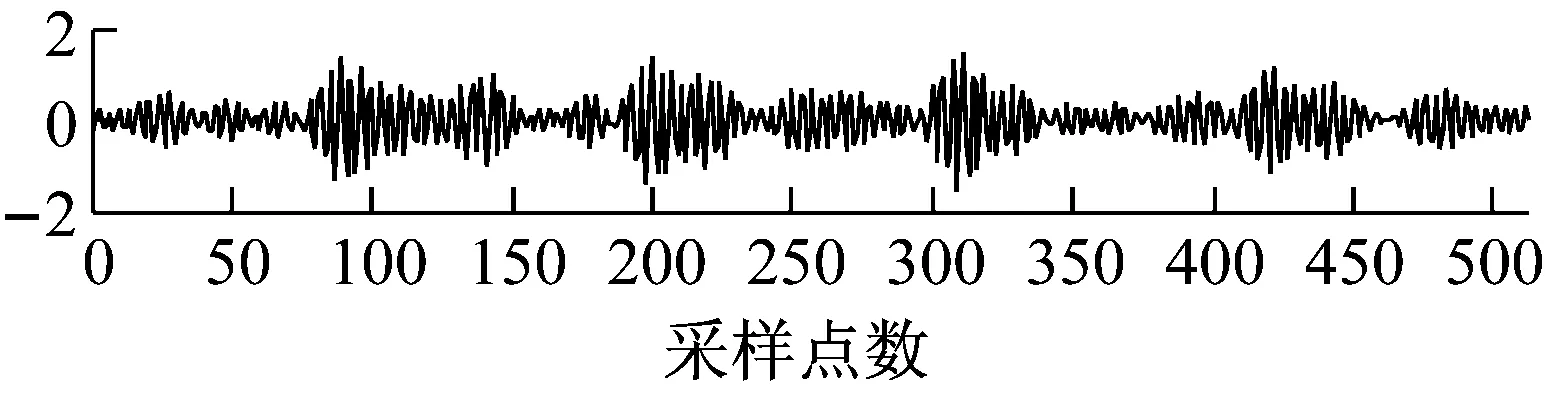
(c) OST-SVD优化矩阵

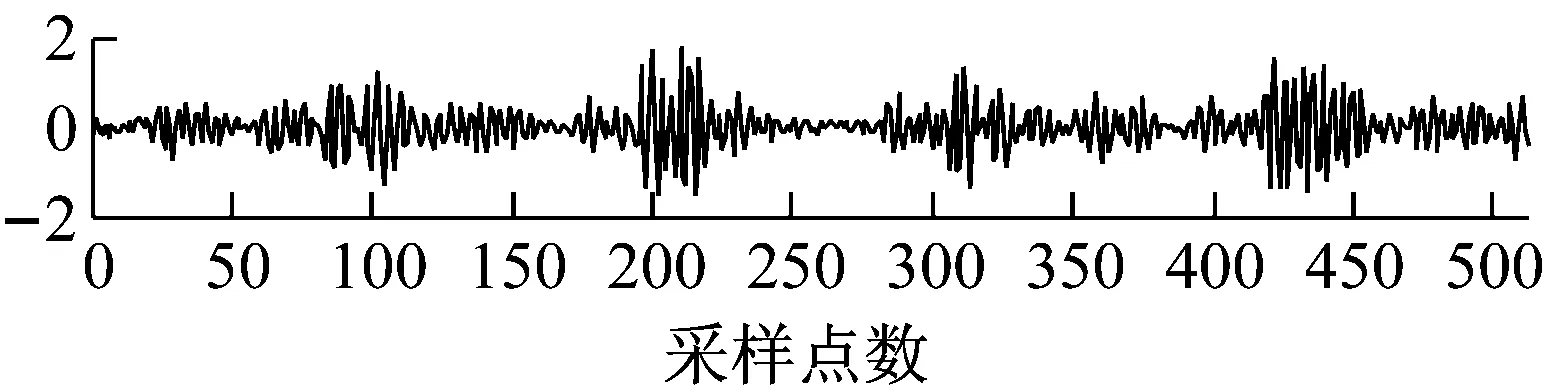
(d) OST-阈值迭代优化矩阵

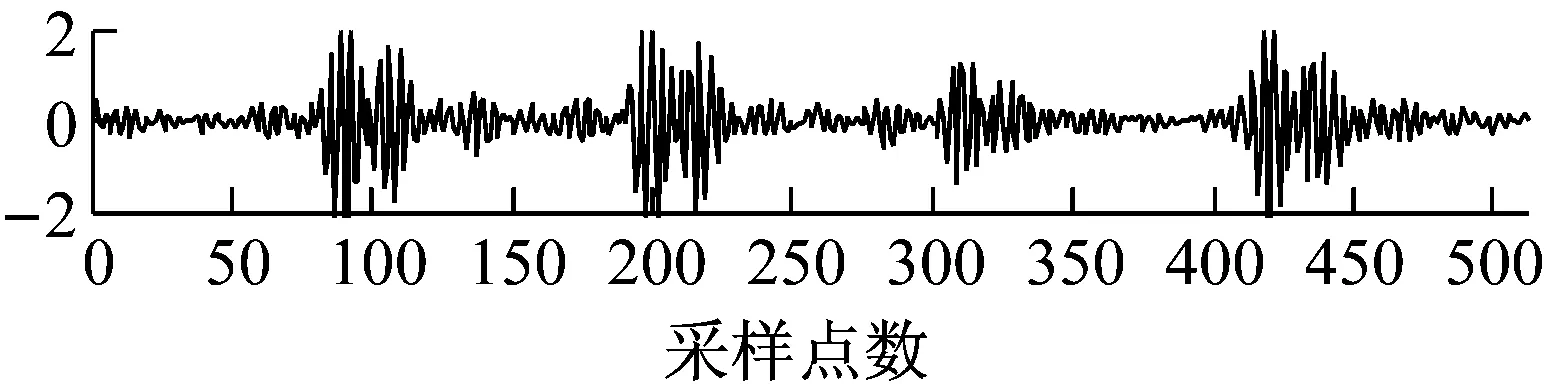
(e) 最优型OST矩阵

图9 压缩率为75%， OST矩阵优化前后重建振动信号与原始信号对比图

Fig.9 A comparison diagram of the reconstructed vibration signals under different matrices with the original vibration signal when the CR is 75%

表3压缩率为75%，不同OST测量矩阵的压缩性能比较

Tab.3Thecomparisonofdifferentmeasurementmatrices’reconstructionperformancewhentheCRis75%

测量矩阵重建误差匹配度 构造时间/sOST矩阵0.653 30.743 50.149OST-阈值迭代优化矩阵0.531 70.818 612.698OST-SVD优化矩阵0.640 20.748 92.926本文最优型OST矩阵0.430 80.829 916.891

表3表明：三种优化方式下的OST测量矩阵相比较，SVD算法优化的OST矩阵重建误差略有减少，阈值迭代算法优化OST矩阵在提高重构精度的同时需要以时间为代价，本文最优型OST矩阵虽然运行时间较长，但其重建误差最小，匹配度最大，因此重建性能最好。

5.2.2 压缩率变化时，最优型OST矩阵的性能分析

图10给出不同优化算法下的OST测量矩阵的重建误差随其压缩率的变化曲线，即当测量值在60～270范围内变化时，不同测量矩阵下振动信号的重建误差。图11给出不同测量矩阵的波形匹配度随压缩率的变化曲线，即不同测量矩阵下重建振动信号与原始振动信号的相似程度比较。

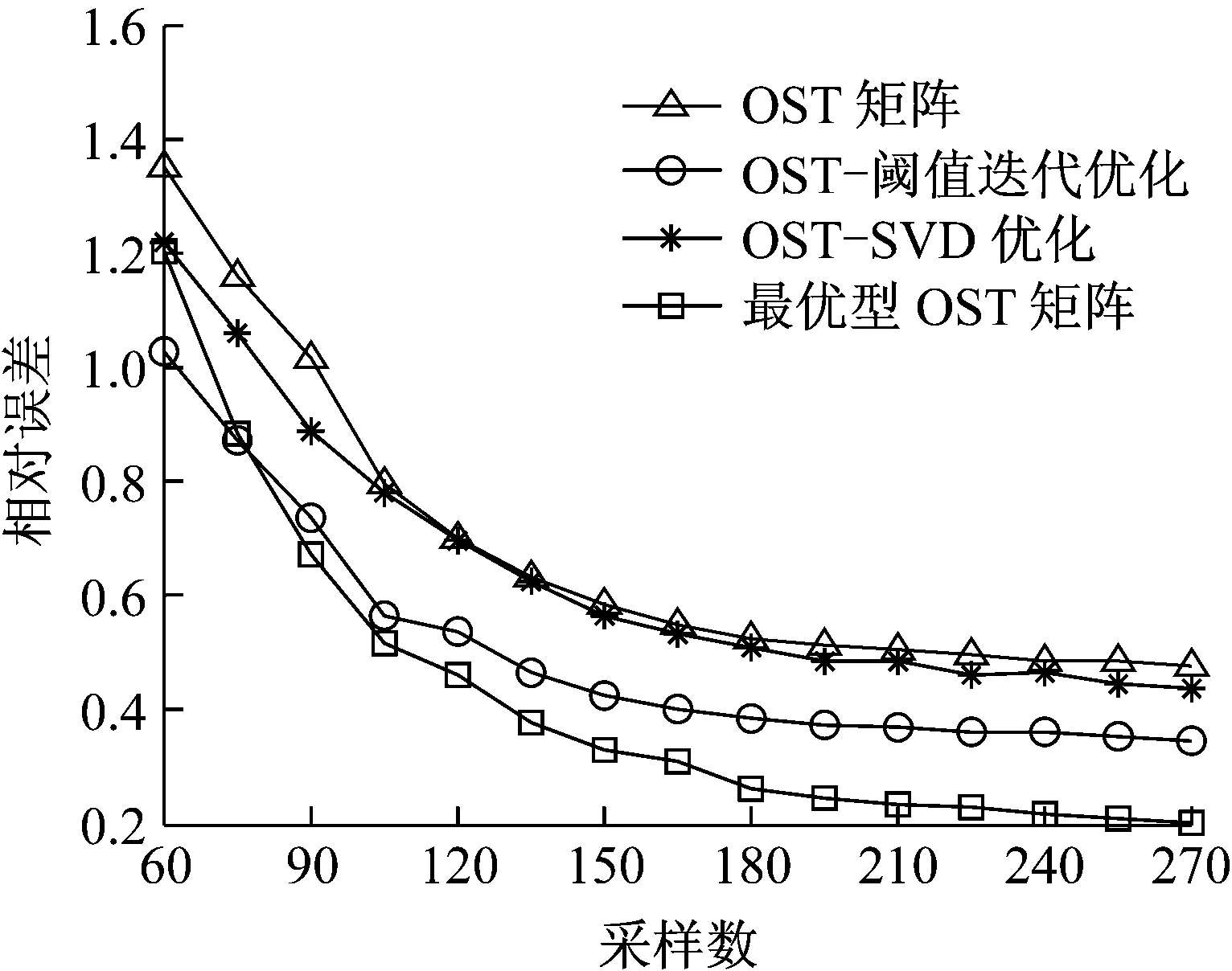
图10 不同算法优化后的OST矩阵重建误差

Fig.10 The reconstruction error under different OST matrices with different optimization algorithms

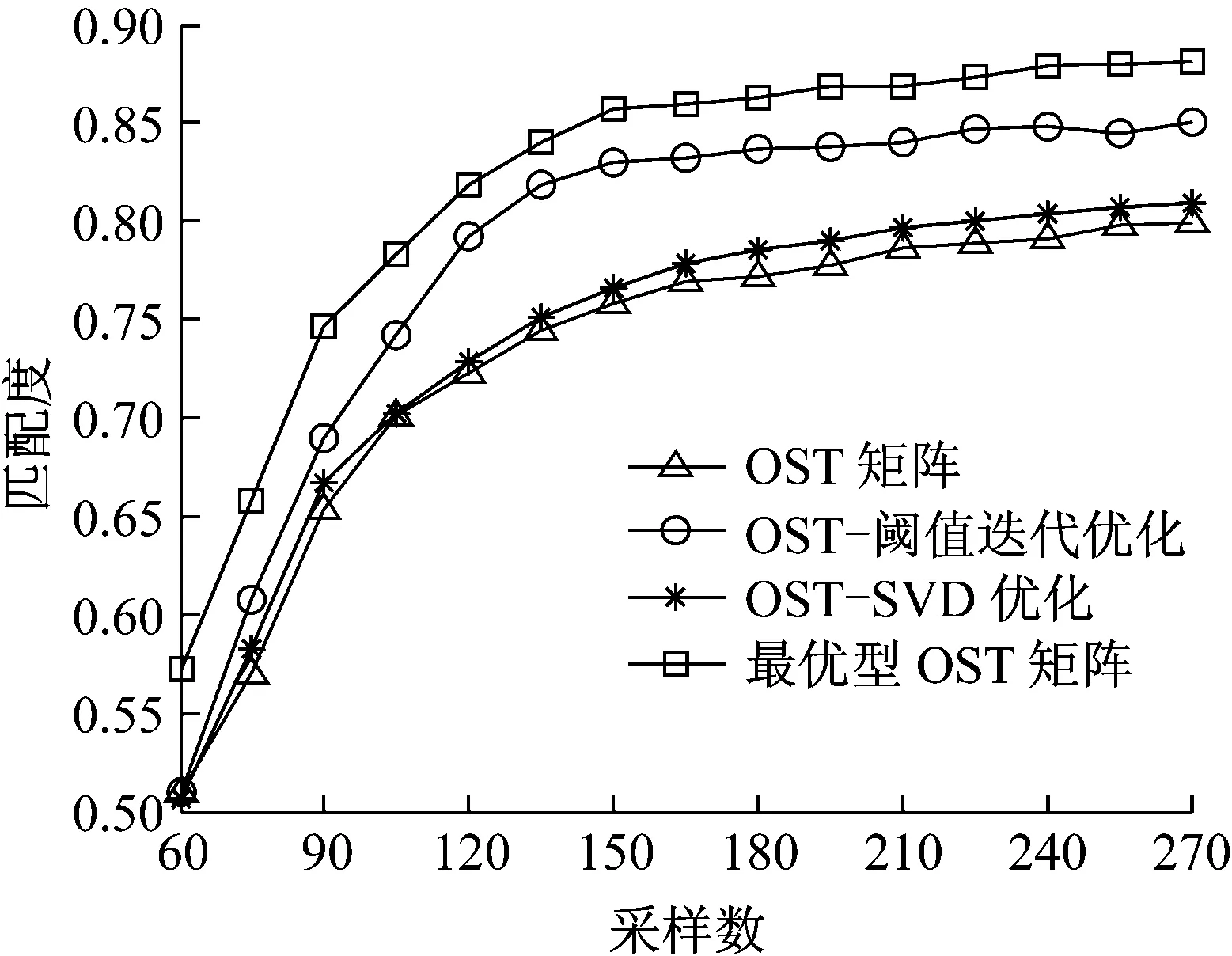
图11 不同算法优化后的OST矩阵重建振动信号的波形匹配度

Fig.11 The reconstructed vibration signal’s degree of waveform matching under different OST matrices with different optimization algorithms

图10表明：相比于未优化的OST矩阵，SVD算法优化的OST矩阵相对误差略有减小，阈值迭代优化的OST矩阵重构误差更小，两种优化方式结合下的最优型OST矩阵的重建误差最小。图11表明：最优型OST测量矩阵下重建信号的波形匹配度最高，说明该矩阵用于振动信号的压缩采集性能最好。

表4表明：随着压缩率的逐渐增大，测量数目逐渐减小，各矩阵的重建误差值也逐渐变大，相比于未优化的OST矩阵，优化后的OST矩阵的重建误差数值明显减少，其中，最优型OST矩阵的重构误差最小，在压缩率为60%时，相对误差值已减小到了0.230 9，同条件下的Toeplitz矩阵重构误差值为0.924 4，同条件下的高斯矩阵重构误差值为0.560 7，明显可以看出最优型OST矩阵相比于Toeplitz矩阵、高斯矩阵及优化前的OST矩阵应用于振动信号的压缩采集有着更好的性能。

表4 不同矩阵的相对误差值Tab.4 Relative errors under different matrices

6 结 论

针对依据传统的奈奎斯特采集定律采集机械振动信号时，需要非常高的采样频率及巨大存储空间的问题，本文将压缩感知理论应用于机械振动信号的采集过程中去。针对压缩感知随机矩阵不易硬件实现的问题，以确定性的Toeplitz矩阵为基础，采用OST测量矩阵对振动信号进行压缩测量。为了解决确定性测量矩阵重构精度较低的问题，采用阈值迭代和SVD分解算法联合优化的方式对OST测量矩阵进行优化，得到的最优型OST测量矩阵可以很好地适用于振动信号的压缩测量，且重构性能优于高斯矩阵、Toeplitz矩阵和优化前的OST矩阵。本文设计的最优型OST测量矩阵和振动信号压缩采集方案具有一定的理论意义与应用价值，针对OST矩阵结构简单易构造的特点，后期将更深层次地开展OST测量矩阵应用于振动信号压缩采集硬件实现的研究。