加载速率对钢筋混凝土梁受剪性能影响的试验研究
2019-04-22易伟建
袁 健, 易伟建
(1.中南林业科技大学 土木工程学院,长沙 410004;2.湖南大学 土木工程学院,长沙 410082)
钢筋混凝土梁在冲击、爆炸等动力荷载作用下会产生高应变率,但由于惯性效应的存在导致难以评估材料应变率对其力学性能的影响[1]。采用接触式单调加载方式并以较快的速率进行钢筋混凝土梁破坏试验,不仅可使构件产生与动力荷载作用效应相当的材料应变率,还能避免惯性效应的干扰,是一种较好的试验手段。
Mahin等[2]进行了4根钢筋混凝土梁受力性能试验研究,结果表明加载速率的增大会使钢筋混凝土梁中钢筋首次屈服时对应的正截面受弯承载力提高,但对构件极限承载力、延性和耗能能力的影响不大。Takeda等[3]、Mutsuyoshi等[4]发现静载作用下钢筋混凝土梁发生弯曲破坏,而加载速率较快时却发生剪切破坏;Kulkarni等[5]的试验研究却得到了相反的结论,解释其主要原因为:不同试验所采用钢筋材料的应变率敏感性存在差异,从而导致出现相反的试验现象。Otani等[6]对4根钢筋混凝土悬臂梁的试验研究发现,加载速率的提高引起纵向受拉钢筋应变率的增大,从而使梁正截面受弯承载力提高7%~20%,但梁的破坏模式未发生改变。Adhikary等[7-9]进行了不同加载速率下72根钢筋混凝土梁受力性能的试验研究,其中最大加载速率为2.0 m/s,纵向受拉钢筋和箍筋应变率的变化范围为10-5~100/s。结果表明,梁的极限承载力、刚度和耗能能力随加载速率的增大而提高;相同速率作用下梁的极限承载力随配箍率的增大而提高;加载速率对梁极限承载力的影响程度随配箍率增大而降低。李敏[10]采用两种不同速率(5.0×10-5m/s和3.0×10-2m/s)进行的16根钢筋混凝土梁正截面受弯性能试验研究发现,梁的承载力随加载速率的增大而提高;随着加载速率的提高,梁的延性和刚度会下降;加载速率未改变梁的破坏模式,但改变了裂缝的分布;材料应变率效应是梁的承载力随加载速率增大而提高的主要原因,而惯性效应可以忽略。肖诗云等[11]以1.0×10-4m/s~1.0×10-2m/s的速率进行了5根钢筋混凝土梁力学性能试验,结果表明不同加载速率下所有梁的破坏形态基本一致,均为弯曲破坏;随着加载速率的提高,梁的开裂荷载、极限荷载、耗能能力、跨中位移以及位移延性系数均明显增大。由此可见,关于加载速率对钢筋混凝土梁破坏模式影响的问题存在分歧,以致结构构件抗震设计及分析时一般未考虑该因素的影响。
为此,本文采用单调加载的方式开展不同速率下6根无腹筋和12根有腹筋矩形截面简支梁受剪性能试验,主要研究加载速率对梁破坏形态和极限承载力的影响,并结合已有的试验数据分析加载速率对钢筋混凝土梁受剪承载力影响的规律。
1 试验概况
1.1 试件设计
本试验设计了六组不同的试件,每组包括3根试验参数完全相同的梁,主要试验参数见表1。其中,试件底部配置3根直径为20 mm的HRB400级纵向受拉钢筋,竖向箍筋采用实测直径为6.3 mm的HPB300级钢筋。

表1 试件主要参数Tab.1 Main parameters of specimens
通过试配确定混凝土配合比,浇筑试件时严格控制材料用量并在同一天内完成。每批混凝土留置6个边长为150 mm的立方体试块,与试件同条件养护至试验阶段。按照《普通混凝土力学性能试验方法标准》[12](GB/T 50081—2002)的规定,以0.6 MPa/s的加载速率实测出混凝土立方体抗压强度平均值fcu,m=46.2 MPa。基于《金属材料拉伸试验—第1部分:室温试验方法》(GB/T 228.1—2010)[13]的相关规定,实测得到纵向受拉钢筋和箍筋试样的准静态屈服强度分别为455 MPa、327 MPa,统一取弹性模量Es=2.0×105N/mm2,则相应的屈服应变分别为2 275 με、1 635 με。
受试验设备加载能力的限制,仅实测了准静态应变率下混凝土和钢筋试样的力学性能参数,而材料的动态强度则根据下列经验公式进行推算。
文献[15]的研究结果表明,应变率对钢筋弹性模量的影响不大,动态屈服强度可按下式进行换算:
(1)
cf=0.170 9-3.289×10-4fym,s
(2)
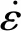
1.2 试验装置和数据量测
为避免产生冲击效应,将作动器前端与梁的上表面完全接触后再进行加载,加载装置如图1所示。
经调试发现,在作动器前端与梁之间增设“垫块”(见图2),可在一定程度上提高梁受力过程中的平均加载速率。其中,垫块由蝶形弹簧、20 mm钢板和5 mm橡胶片组成。为考察垫块的受力性能,将垫块放置在混凝土立方体试块上并利用万能试验机进行加载。结果表明,当加载至18.0 kN时,垫块中的蝶形弹簧大致被压平,垫块的总变形约为2.5 mm。此外,还设计了一套平衡支座用于测试梁的支座反力,如图3所示。图3中支座底板两端各设置一个圆孔,导向轴伸至圆孔深度的一半处并预留一定的间隙。支座直接放置在荷载传感器上,上部荷载全部由荷载传感器承担,导向轴仅起限位作用。
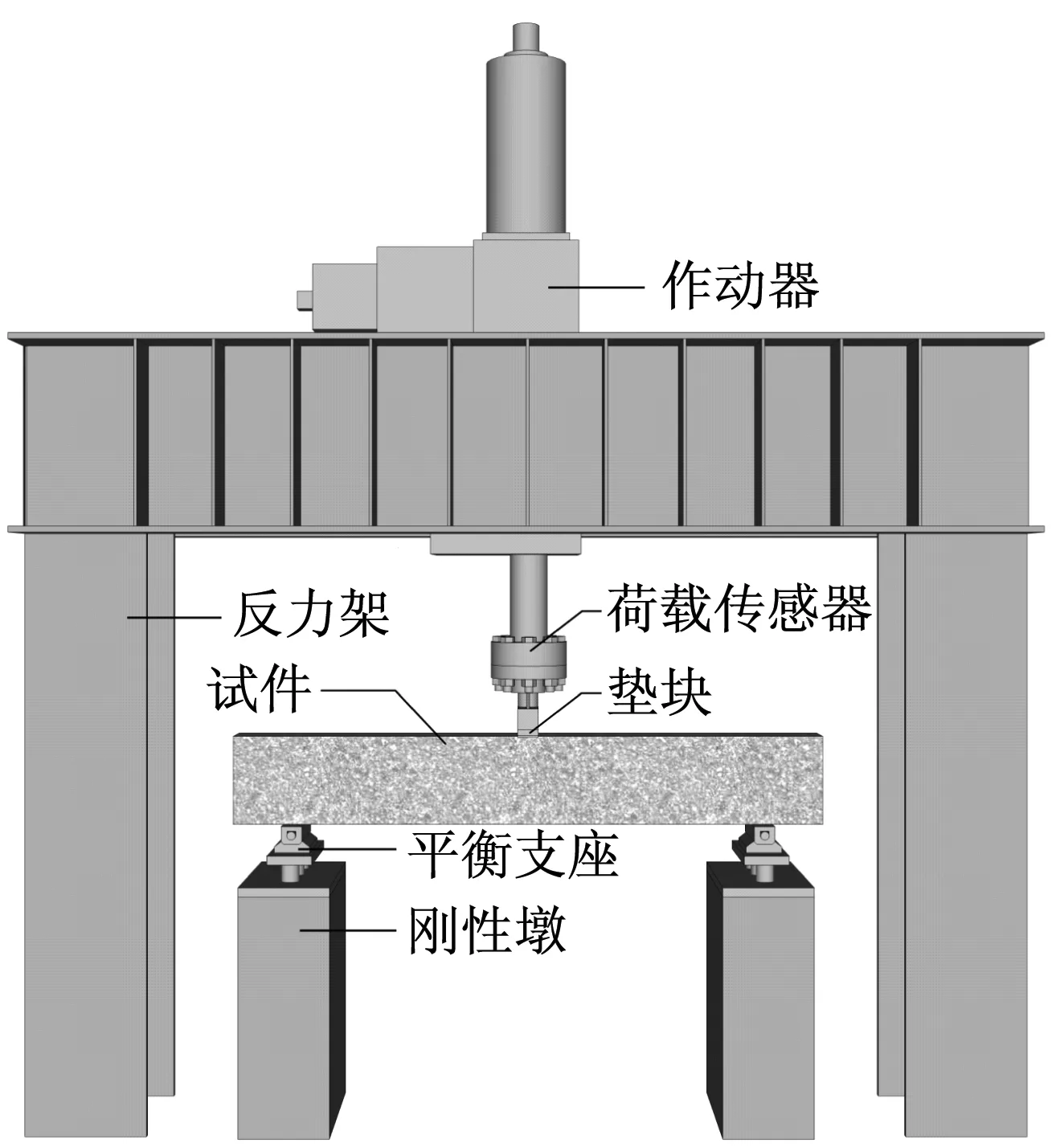
图1 试验装置Fig.1 Test set-up

图2 垫块Fig.2 Block

图3 平衡支座Fig.3 Balance support
以电液伺服试验系统的最佳性能进行梁的预试验,得到梁跨中位移时程曲线,如图4所示。结果表明,当加载至8.8 ms时,梁所受到的荷载为18.0 kN,此时蝶形弹簧已被压平,梁跨中位移仅0.14 mm。经分析,梁的主要受力过程(A~B点之间曲线)的平均加载速率为3.5×10-1m/s。
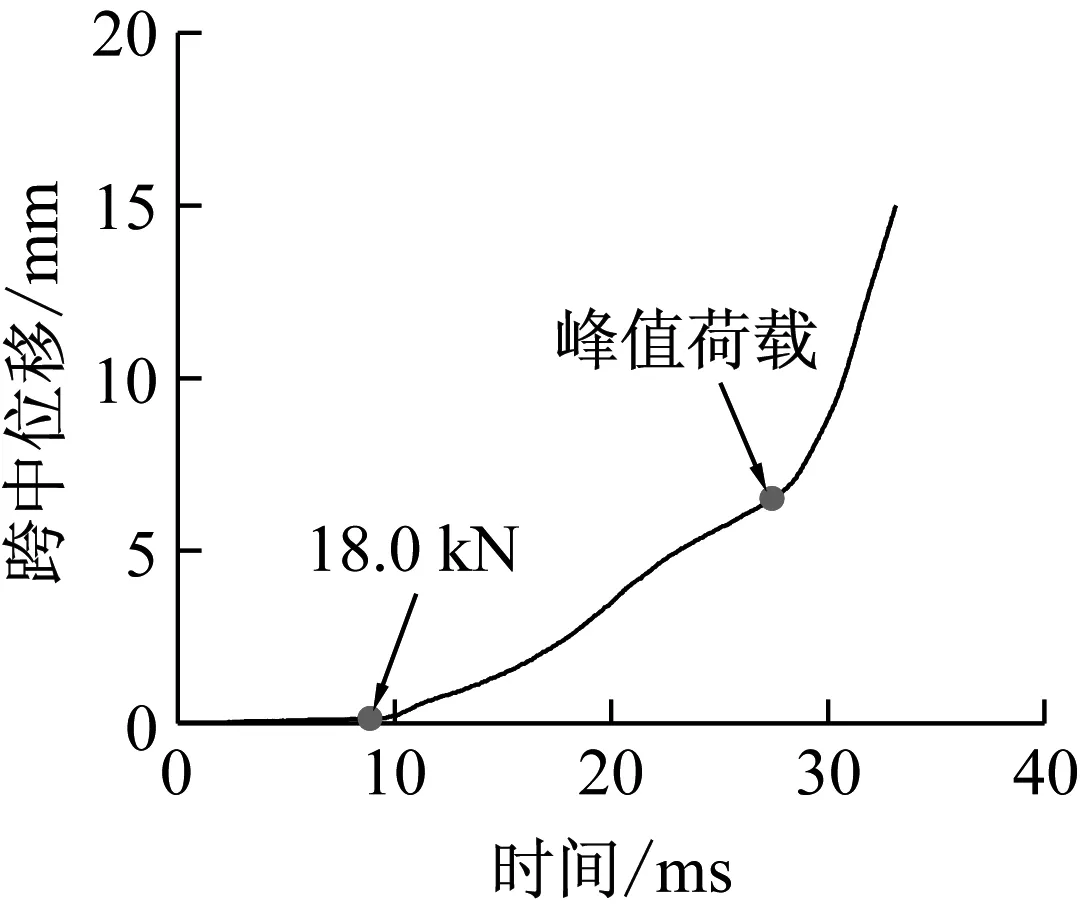
图4 预试验梁的跨中位移时程曲线Fig.4 Midspan displacement-time curve of trial test beam
在梁的上表面且距跨中h0/2处粘贴混凝土应变片,纵向受拉钢筋的跨中处及箍筋的一半高度处布置钢筋应变片,在跨中处安装电子尺测量梁跨中截面的实际位移。试验过程中,采用高速摄像机记录破坏形态,本试验设置为1 000帧/秒。试验采用位移控制进行接触式单调加载,加载波形为三角波,目标位移设置为30 mm,试验时采用的加载速率和采样频率见表2。其中,准静态速率、中等速率和快速加载分别采用S、M和H进行标识。

表2 加载速率及采样频率Tab.2 Loading rate and sampling frequency
2 试验结果与分析
2.1 加速度响应及惯性效应分析
为考察快速荷载作用下梁的惯性效应,在剪跨比为2.3的无腹筋梁侧面安装7个加速度传感器测试梁的竖向加速度,如图5所示。

图5 加速度传感器布置Fig.5 Arrangement of accelerometers
以蝶形弹簧被压平的前1 ms为起点,通过低通滤波(上限频率取1 000 Hz)得到加速度时程曲线,如图6所示。其中,负值表示向下的加速度,正值表示向上的加速度。图6表明,随着测试截面距跨中距离的增大,加速度响应依次出现了延时。尽管延时程度并不显著,但在一定程度上反映了快速荷载作用下梁中应力波的传播过程。A2~A6的初始加速度方向向下,且传感器距跨中越远,加速度峰值越大;A1、A7的初始加速度方向向上,当达到峰值后下降并改变方向。10 ms以后,A3和A5产生了较大的加速度,这与测点附近出现了斜裂缝有关。

(a) A1~A4

(b) A4~A7图6 加速度时程曲线Fig.6 Acceleration time history curves
将跨中荷载、支座反力和惯性力时程曲线进行比较,如图7所示。其中,跨中荷载指作动器在梁跨中处施加的集中荷载,以向下为正;支座反力指两个平衡支座中压力传感器的读数之和,以向上为正;惯性力以向上为正,并近似按下式计算:
A5(t))×0.20+(A2(t)+A6(t))×0.205+
(A1(t)+A7(t))×0.19]
(3)


图7 跨中荷载、支座反力和惯性力比较Fig.7 Comparison of mid-span load, support reaction and inertia force
图7表明,支座反力及惯性力之和能较好地与跨中荷载吻合。5 ms以内,由于作动器处于加速过程而导致支座反力与跨中荷载相差较大;5 ms后至梁破坏,支座反力与跨中荷载吻合较好。经比较,截止于跨中荷载达到峰值时刻(19.62 ms),惯性力的变化范围为-18.5~25.5 kN。其中,13.04 ms至19.62 ms阶段,惯性力与跨中荷载之比恒小于5.0%。由此可见,快速荷载作用下梁的惯性效应不显著,可忽略不计。
2.2 无腹筋梁的试验结果及分析
2.2.1 无腹筋梁的破坏形态
由于采用位移控制加载方式且目标值远大于梁破坏时的位移,故需从录像中截取梁的破坏形态,如图8所示。受高速摄像机像素的限制,竖向弯曲裂缝几乎看不清楚,但主要斜裂缝都非常明显。其中,BN-3.0系列梁的一侧剪跨段破坏时,另一侧剪跨段内还未出现任何斜裂缝,为典型的斜拉破坏。BN-2.3系列梁出现斜裂缝后,仍能继续承载直到发生剪压破坏。
此外,图9所示试件BN-2.3-H的斜裂缝发展过程为:5 ms时,在加载点下方附近的梁腹部出现了“八字形”斜裂缝,但未向加载点和梁底贯通;8 ms时,又相继在外侧出现了两条斜裂缝并向加载点和支座附近延伸,其中一条斜裂缝将发展成临界斜裂缝;18 ms时,临界斜裂缝已完全形成且受压区混凝土也被严重压碎,从而导致试件发生剪切破坏。

(a) BN-2.3系列

(b) BN-3.0系列图8 无腹筋梁的破坏形态Fig.8 Failure modes of beams without web reinforcement

图9 试件BN-2.3-H的斜裂缝发展过程
Fig.9 Development process of diagonal crack of specimen BN-2.3-H
2.2.2 无腹筋梁的主要试验结果
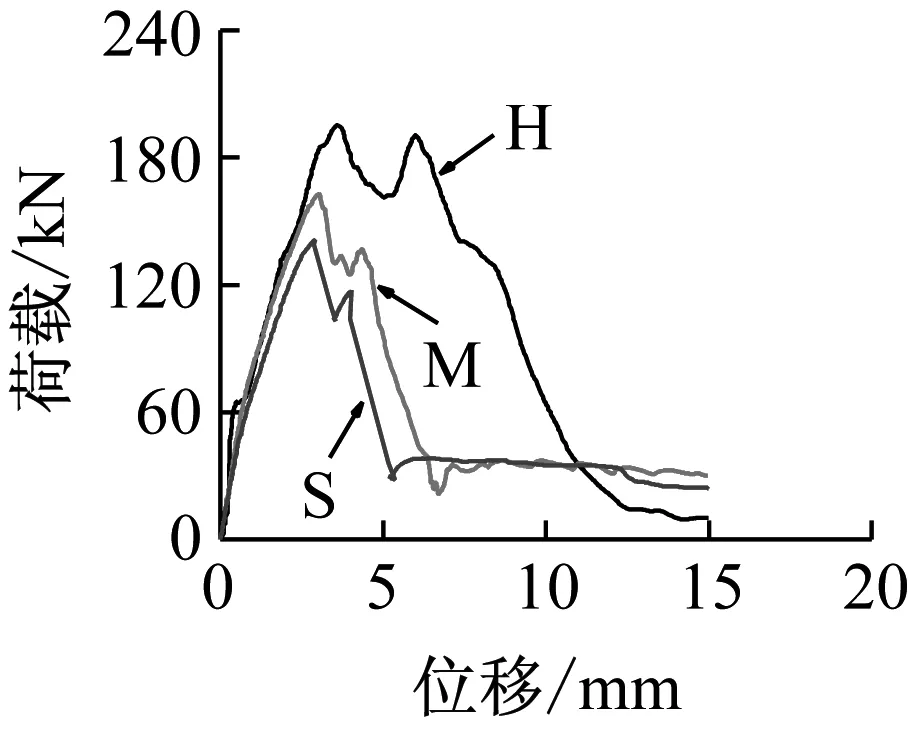
不同加载速率下无腹筋梁的荷载-跨中位移曲线如图10所示,主要试验结果见表3。自开始加载至峰值荷载,无腹筋梁跨中处纵向受拉钢筋应变与位移的关系,如图11所示。
(a) BN-2.3系列
(b) BN-3.0系列图10 无腹筋梁的荷载-跨中位移曲线Fig.10 Load-midspan displacement curves of beams without web reinforcement
结合图10和表3可知,达到峰值荷载前,不同加载速率下无腹筋梁的荷载-跨中位移曲线基本重合,峰值荷载及对应的跨中位移均随加载速率的提高而增大。实测得到的纵向受拉钢筋应变率量级为10-4~10-1/s、受压区混凝土应变率量级为10-5~10-2/s,相当于从准静态荷载至地震作用下的材料应变率[16-18]。相同量级的加载速率下,BN-2.3系列梁的受剪承载力增大系数CIF值高于BN-3.0系列梁,表明加载速率对剪跨比较小的无腹筋梁受剪承载力的影响更加显著。

表3 无腹筋梁的主要试验结果Tab.3 Test results of beams without web reinforcement

(a) BN-2.3

(b) BN-3.0图11 无腹筋梁的纵向受拉钢筋应变-跨中位移关系
Fig.11 Relationship of strain of longitudinal tensile reinforcement and midspan displacement of beams without stirrups
图11表明,当达到峰值荷载时,试件BN-2.3-H的纵向受拉钢筋已达到屈服强度,而其余试件的纵向受拉钢筋均未屈服。纵向受拉钢筋屈服引起较大变形使得混凝土裂缝进一步发展并导致受压区混凝土被压碎而发生弯剪破坏,破坏时的剪力大小在一定程度上取决于梁的抗弯屈服能力。由此可见,加载速率的提高,已改变了无腹筋梁的抗剪机理。无腹筋梁受剪承载力随加载速率的提高程度不能简单地在准静态作用时的计算式中考虑材料应变率效应后直接算出,而应根据试验结果确定。
2.3 有腹筋梁的试验结果及分析
2.3.1 有腹筋梁的破坏形态
不同加载速率下钢筋混凝土有腹筋梁的破坏形态,如图12所示。与准静态速率相比,快速荷载作用下梁的斜裂缝数量增多且受压区混凝土被压碎的现象更加严重,其中剪跨比较小的梁中该现象尤为突出。由于箍筋的作用,临界斜裂缝下端沿纵向受拉钢筋撕脱的现象没有无腹筋梁那么明显。

(a) BS-2.3-1系列

(b) BS-2.3-2系列

(c) BS-3.0-1系列

(d) BS-3.0-2系列图12 有腹筋梁的破坏形态Fig.12 Failure modes of beams with stirrups
2.3.2 有腹筋梁的主要试验结果
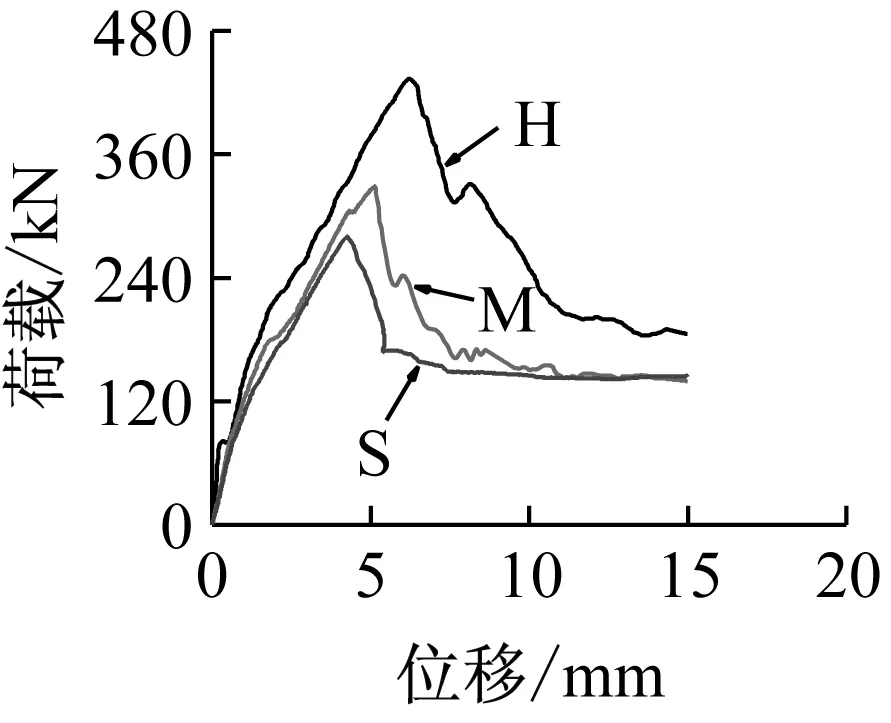
不同加载速率下钢筋混凝土有腹筋梁的荷载-跨中位移曲线见图13,主要试验结果见表4。当荷载为1/4Pmax、2/4Pmax、3/4Pmax和Pmax时,有腹筋梁的纵向受拉钢筋应变-位移变化趋势如图14、图15所示;箍筋应变变化趋势如图16、图17所示。图14~图17中的虚线表示钢筋屈服应变,图16和图17中的横坐标代表箍筋位置(箍筋距左支座中心的距离)。
(a) BS-2.3-1

(b) BS-2.3-2

(c) BS-3.0-1

(d) BS-3.0-2图13 有腹筋梁的荷载-跨中位移曲线Fig.13 Load-midspan displacement curves of beams with stirrups表4 有腹筋梁的主要试验结果Tab.4 Test results of beams with stirrups
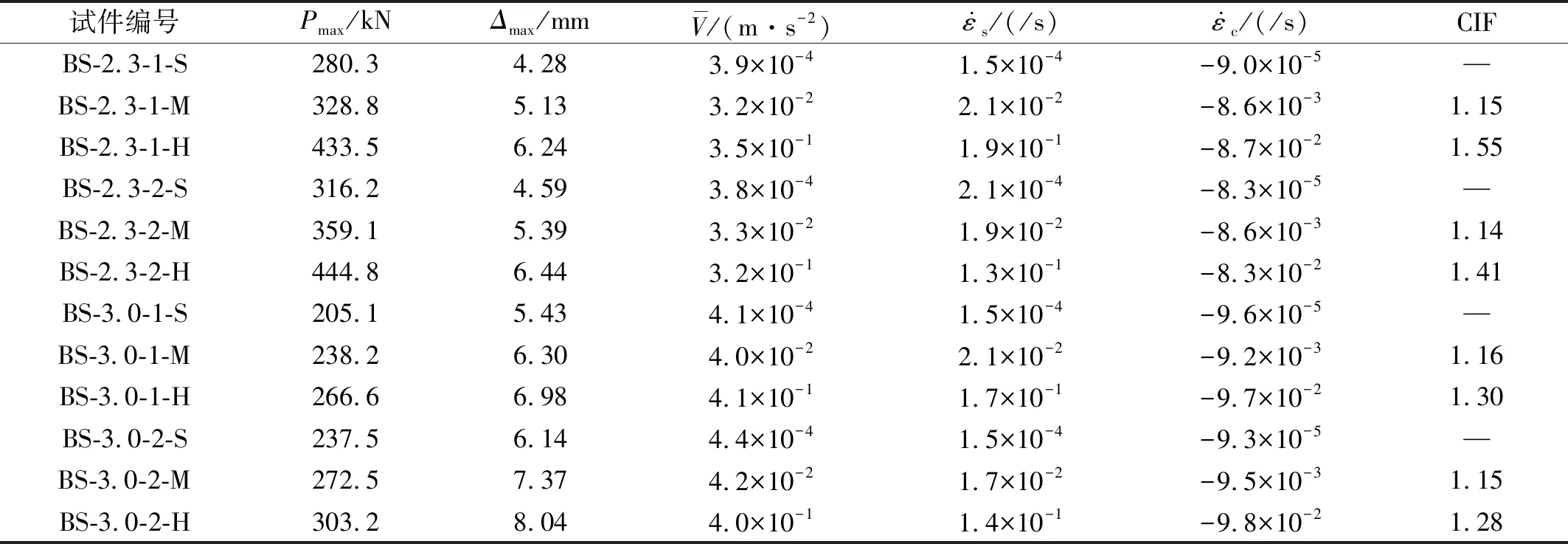
试件编号Pmax/kNΔmax/mmV/(m·s-2)ε·s/(/s)ε·c/(/s)CIFBS-2.3-1-S280.34.283.9×10-41.5×10-4-9.0×10-5—BS-2.3-1-M328.85.133.2×10-22.1×10-2-8.6×10-31.15BS-2.3-1-H433.56.243.5×10-11.9×10-1-8.7×10-21.55BS-2.3-2-S316.24.593.8×10-42.1×10-4-8.3×10-5—BS-2.3-2-M359.15.393.3×10-21.9×10-2-8.6×10-31.14BS-2.3-2-H444.86.443.2×10-11.3×10-1-8.3×10-21.41BS-3.0-1-S205.15.434.1×10-41.5×10-4-9.6×10-5—BS-3.0-1-M238.26.304.0×10-22.1×10-2-9.2×10-31.16BS-3.0-1-H266.66.984.1×10-11.7×10-1-9.7×10-21.30BS-3.0-2-S237.56.144.4×10-41.5×10-4-9.3×10-5—BS-3.0-2-M272.57.374.2×10-21.7×10-2-9.5×10-31.15BS-3.0-2-H303.28.044.0×10-11.4×10-1-9.8×10-21.28

(a) BS-2.3-1-S
(b) BS-2.3-1-M
(c) BS-2.3-1-H

(d) BS-2.3-2-S

(e) BS-2.3-2-M
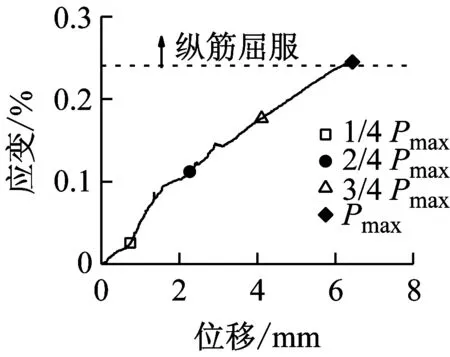
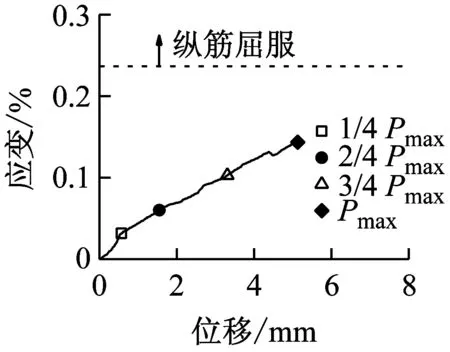
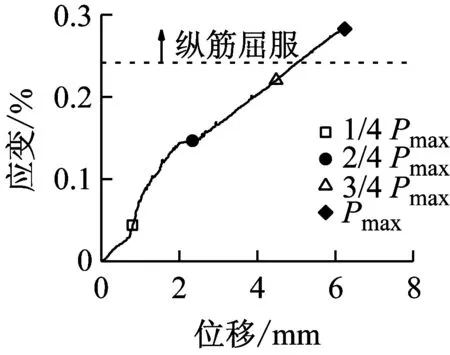
(f) BS-2.3-2-H图14 BS-2.3系列梁的纵筋应变-跨中位移曲线Fig.14 Strain of longitudinal tensile reinforcement-midspan displacement cures of specimen BS-2.3
由图13~图17和表4可知,有腹筋梁的峰值荷载和跨中位移均随加载速率的提高而增大;当荷载达到峰值后,有腹筋梁的荷载-位移曲线突然下降。加载点两侧的剪跨段都出现了斜裂缝,且箍筋均先于纵向受拉钢筋达到屈服强度,表明所有试件发生剪压破坏。从整体上看,剪跨比较小的有腹筋梁受剪承载力随加载速率增大而提高的幅度更显著。
比较表3和表4可见,随着加载速率的提高,大多数有腹筋梁的受剪承载力增大系数小于无腹筋梁的。从机理上看,加载速率对无腹筋梁受剪承载力的影响与剪切破坏形态及剪跨比有关,且混凝土材料的率敏感性高于钢筋,导致无腹筋梁受剪承载力随加载速率增大而提高的幅度更显著。此外,尽管试件BS-2.3-1-S和BS-3.0-1-S的配箍率略小于最小配箍率,但其受剪承载力比相应的无腹筋梁分别提高了63.8%、45.2%,说明箍筋较好地发挥了作用。
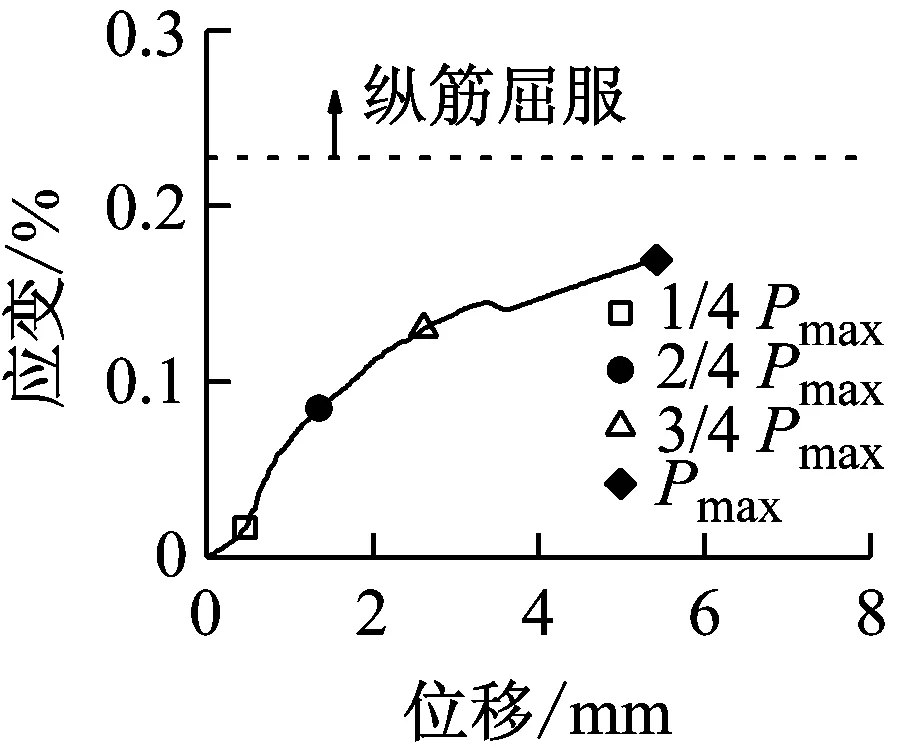
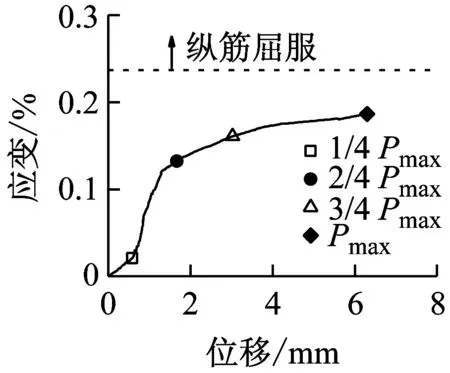
图14和图15表明,随着加载速率的提高,峰值荷载对应的纵向受拉钢筋应变呈增大趋势。当达到峰值荷载时,有腹筋梁的纵向受拉钢筋在准静态和中等速率荷载作用下均未屈服,而快速荷载作用下都达到屈服强度。从图16和图17可以看出,各试件中均有部分箍筋达到屈服强度,且箍筋应变呈非均匀分布。部分箍筋受局部应力或斜裂缝闭合的影响而处于受压状态,导致其应变随着荷载的增大反而减小,甚至出现压应变。对于准静态和中等速率荷载作用下的有腹筋梁,箍筋应变基本上在剪跨段呈现出大致对称的两个峰值,而加载点附近的箍筋应变相对较小;对于快速荷载作用下试件BS-2.3-1-H和BS-2.3-2-H,其箍筋应变仅在跨中位置附近出现单峰,这是由于加载点附近的混凝土首先被压溃,从而导致箍筋弯折而达到屈服强度。
(a) BS-3.0-1-S
(b) BS-3.0-1-M
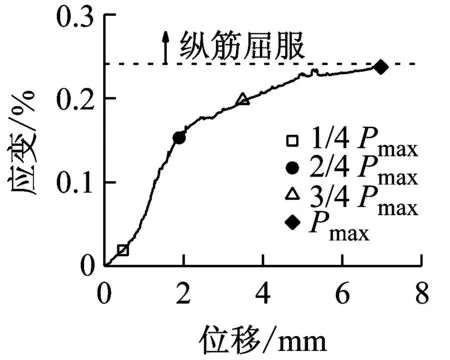
(c) BS-3.0-1-H

(d) BS-3.0-2-S
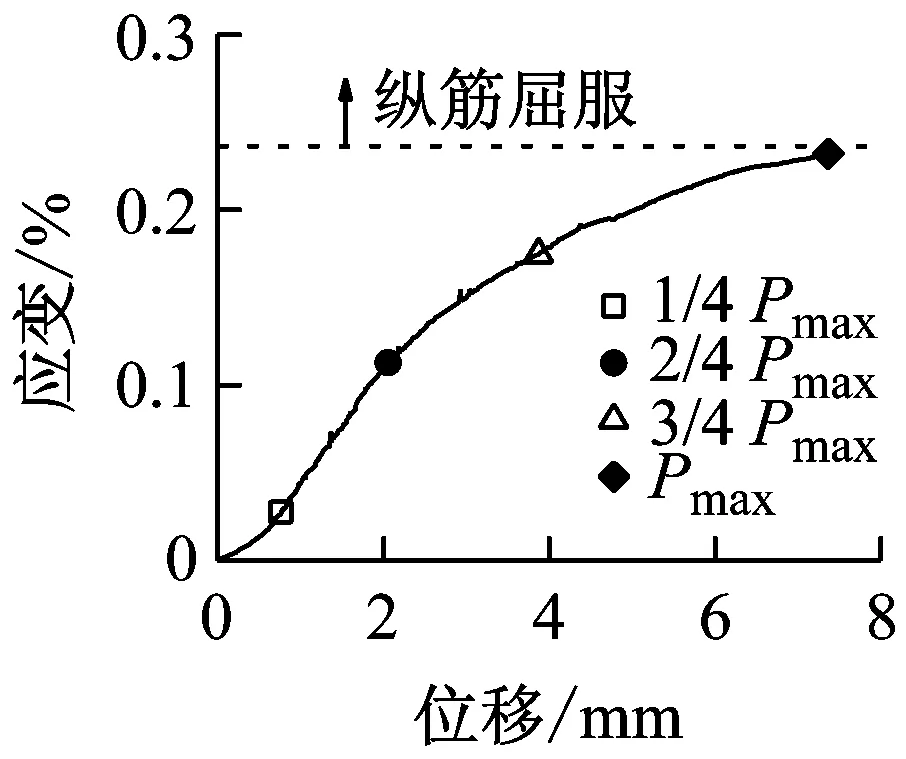
(e) BS-3.0-2-M
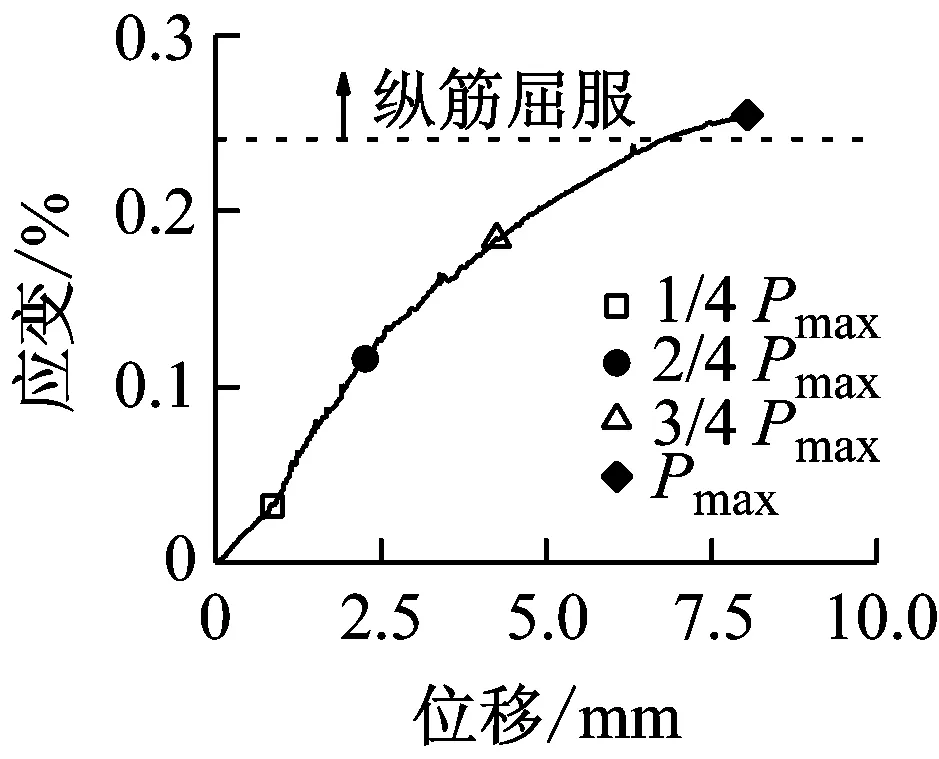
(f) BS-3.0-2-H图15 BS-3.0系列梁的纵筋应变-跨中位移曲线Fig.15 Strain of longitudinal tensile reinforcement-midspan displacement cures of specimen BS-3.0

(a) BS-2.3-1-S

(b) BS-2.3-1-M

(c) BS-2.3-1-H

(d) BS-2.3-2-S
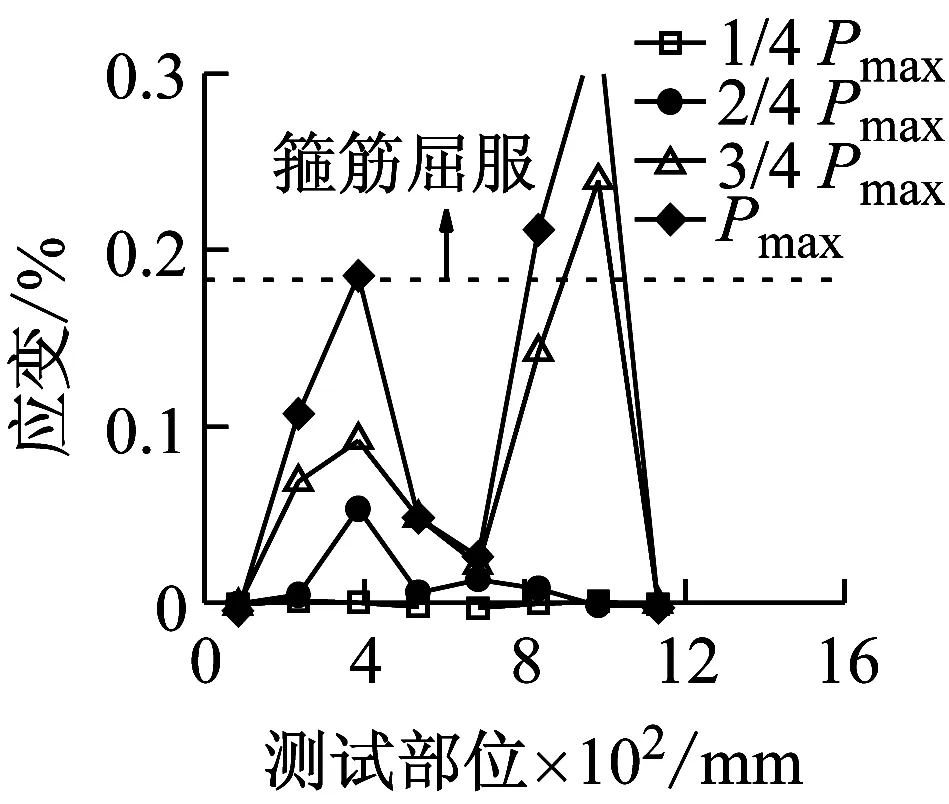
(e) BS-2.3-2-M
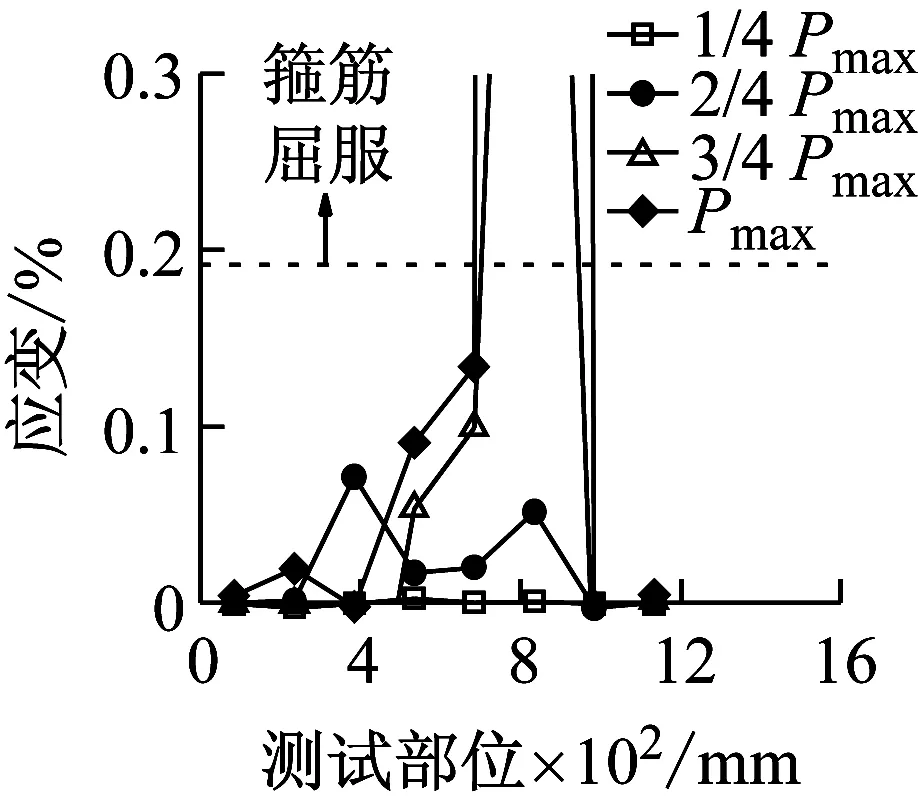
(f) BS-2.3-2-H图16 BS-2.3系列梁的箍筋应变分布Fig.16 Strain of stirrup-midspan displacement cures of specimen BS-2.3
3 加载速率对钢筋混凝土梁受剪承载力的影响分析
文献[9,19]收集整理的不同加载速率下钢筋混凝土矩形截面简支梁试验数据中,Fujikake等[20]完成的6根冲击荷载作用下钢筋混凝土梁也被纳入了。由于冲击荷载试验的惯性效应显著,在支座反力未知的情况下难以将其排除,故应区别对待这两类试验。
本文按以下准则进行筛选试验数据:①发生剪切破坏;②试验参数完整,能满足分析需要;③采用接触式加载;④同条件的梁至少为两根,采用两种或多种不同速率进行加载,且其中一根梁为准静态荷载试验。整理得到无腹筋和有腹筋矩形截面简支梁各27根,数据来源见表5。需要说明的是,Adhikary等[9]于2014年完成的24根梁均未直接给出峰值荷载值,本文通过量测荷载-跨中位移曲线确定其极限承载力。
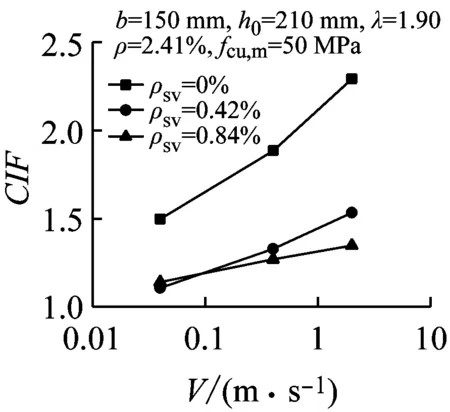
经整理,钢筋混凝土梁受剪承载力增大系数CIF随加载速率的变化趋势,如图18和图19所示。结果表明,不论是无腹筋梁还是有腹筋梁,其受剪承载力增大系数都随加载速率的提高而增大。当其他条件相同时,剪跨比较小的梁受剪承载力增大系数明显高于剪跨比较大的梁。除图19(d)中ρsv=0.15%系列梁以外,其余试件的受剪承载力增大系数呈现出随配箍率提高而减小的趋势。
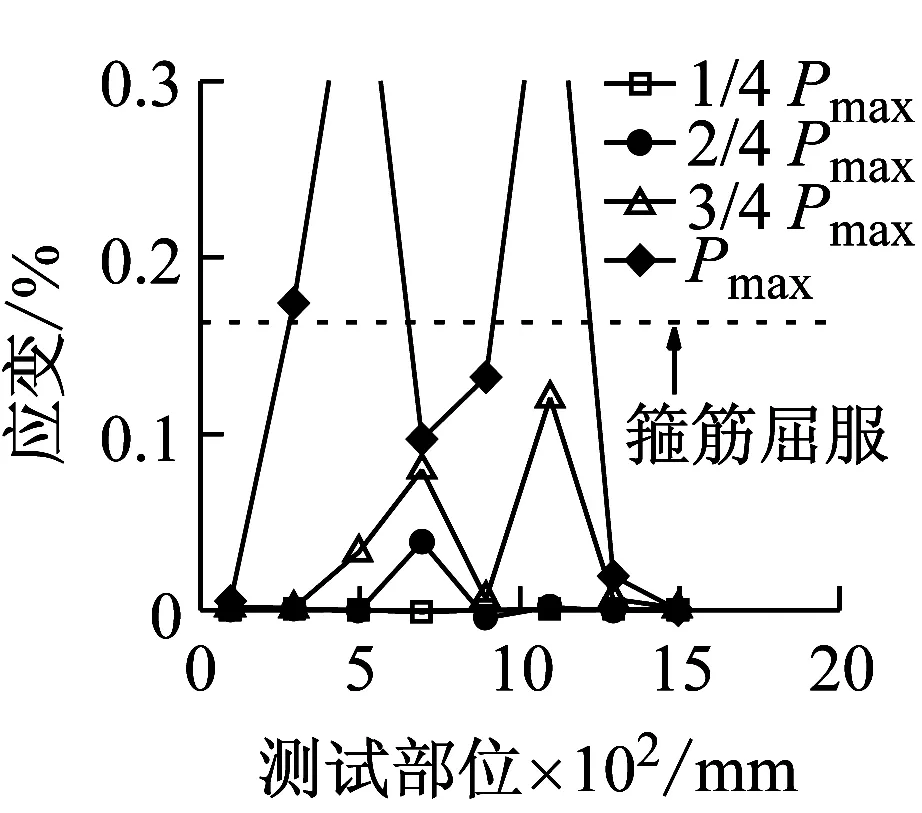
(a) BS-3.0-1-S

(b) BS-3.0-1-M
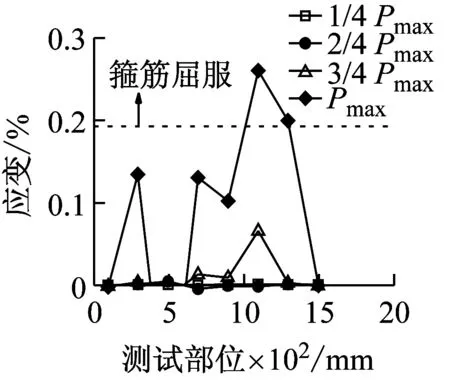
(c) BS-3.0-1-H

(d) BS-3.0-2-S

(e) BS-3.0-2-M
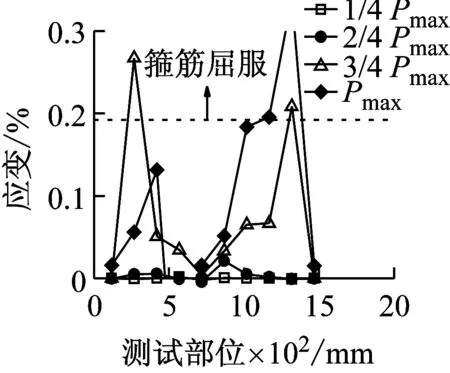
(f) BS-3.0-2-H图17 BS-3.0系列梁的箍筋应变分布Fig.17 Strain of stirrup-midspan displacement cures of specimen BS-3.0表5 不同加载速率下钢筋混凝土梁受剪试验数据统计
Tab.5Statisticsoftestdataofreinforcedconcretebeamsunderdifferentloadingrate

数据来源试件总数按准则①~③筛选筛除数量未引用的依据不满足准则④的数量引用数量无腹筋梁有腹筋梁文献[4]27141)6770文献[5]1491)3220文献[7]2481)—1688文献[8]2472)—17611文献[9]24121)—1248

(b) 文献[7-9]的数据图18 加载速率对无腹筋梁受剪承载力的影响
Fig.18 Effect of loading rate on shear capacity of beams without web reinforcement
4 结 论
(1) 采用电液伺服试验系统以3.5×10-1m/s的速率进行接触式加载,实测得到钢筋混凝土梁的惯性效应不显著,可忽略不计。

(a) 本文试验数据

(b) 文献[7]的数据
(c) 文献[8]的数据

(d) 文献[9]的数据图19 加载速率对不同配箍率梁的影响
Fig.19 Effect of loading rate on shear capacity of beams without web reinforcement
(2) 随着加载速率的提高,梁的峰值荷载及跨中位移均增大,材料的应变率也随之增大;梁的破坏形态出现从纵向受拉钢筋屈服前的剪切破坏向弯剪破坏的转变,同时也改变了裂缝的分布。材料应变率效应是快速荷载作用下梁受剪承载力提高的主要原因。
(3) 钢筋混凝土梁受剪承载力增大系数随加载速率的提高而增大。当加载速率相同时,剪跨比较小的梁受剪承载力增大系数明显高于剪跨比较大的梁,且受剪承载力增大系数总体上随配箍率提高而减小。
(4) 由于抗剪机理发生变化,钢筋混凝土梁受剪承载力随加载速率的提高程度不能简单地在准静态作用时的计算式中考虑材料应变率效应后直接算出,而应根据试验结果确定。
