C形环在超高压大直径容器密封上的适应性研究*

(1.西南石油大学机电工程学院 四川成都 610500;2.石油天然气装备教育部重点实验室 四川成都 610500;3.宝鸡石油机械有限责任公司 陕西宝鸡721002)

随着能源需求的不断增加，产业向深海拓展是未来石化发展的必然趋势；另外在研的11 000 m级载人潜水器“彩虹鱼”拟于2019年挑战马里亚纳海沟，这些工作在超高压工况环境下的大直径容器对密封性能提出更高的要求。因此，针对大直径容器要求和超高压工况环境下密封组件的研究有着重大实践意义。目前成熟的超高压密封方式很难满足直径超过2 m的大直径压力容器密封需求，为解决大直径密封难题，本文作者借鉴已成功运用在直径4 m的反应堆压力容器中的内置弹簧金属C形密封环，来探讨C形环在超高压大直径容器密封上的应用。

当前国内外对C形密封环进行一些研究，SASSOULAS等[1]使用二维轴对称模型较系统地研究了C形密封环的密封性能；李文静等[2]建立了C形密封环三维弹塑性有限元分析模型，通过实验验证该理论模型的可靠性，并分析弹簧结构参数对C形密封环力学行为和密封性能的影响；贾晓红等[3]建立了C形密封环的三维有限元模型，分析了接触区域和接触压力的变化规律；LIU等[4]讨论了C形密封环的可重复使用性，通过二维非线性有限元分析，从理论上验证了密封环重复使用的可能性；LIN等[5]采用三维模型分析了反应堆压力容器在不同温度下的瞬态接触密封分析；励行根等[6]介绍反应堆压力容器用C形密封环的主要制造工艺和技术关键。

目前，国内外对C形密封环的研究相对偏少，且主要是针对C形密封环在压缩工况下的力学性能和密封特性研究，外压影响密封特性的研究较少，且尚无在超高压环境中的研究和使用。因此本文作者针对超高压大直径压力容器建立C形密封环二维轴对称模型，利用Abaqus进行有限元分析，对金属C形环的弹塑性接触变形进行了研究，为超高压环境下密封环的使用提供了理论参考。

1 C形密封环模型的建立

以外径D=318 mm的C形密封环为算例进行分析[7]，其结构如图1所示，各材料基本属性[8]如表1所示。建模分析选定的组合密封环基本结构参数如表2所示。

图1 C形密封环截面结构图

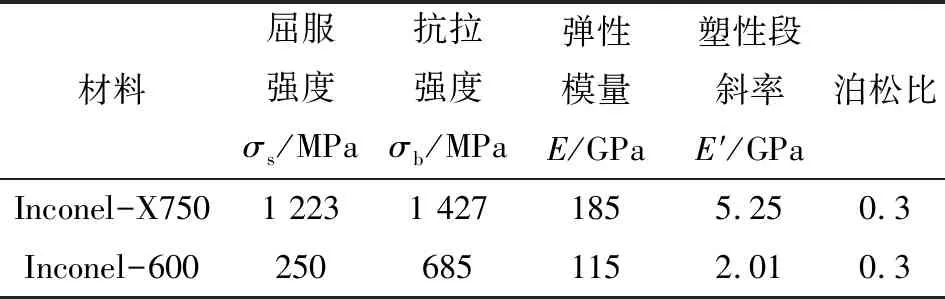
材料屈服强度σs/MPa抗拉强度σb/MPa弹性模量E/GPa塑性段斜率E′/GPa泊松比Inconel-X7501 2231 4271855.250.3Inconel-6002506851152.010.3

表2 C形密封环结构参数

C形密封环沿周向对称，建立密封环和上下筒体的二维轴对称模型。常见的C形密封环截面由内到外分别为螺旋弹簧、内层金属包覆层和外层包覆层3部分。外层包覆层通常选用质地较软的银层(厚度0.3 mm)，其良好的延展性可以弥补接触密封面的缺陷，但高压会使银层发生毁坏，高压下应去除银层，保留螺旋弹簧和内层金属包覆层。文中对比分析了有银层和无银层C形密封圈的压缩回弹特性，以验证银层对密封环压缩特性的影响，并验证模型的正确性[9]。

有限元模型中上下筒体设为解析刚体，考虑到C形环变形时材料发生塑性流动和塑性硬化，采用双线性等强度强化材料模型模拟材料的弹塑性。在压缩加压过程中，C形环和弹簧以及C形环与密封面之间接触会产生摩擦，因此在各接触表面建立摩擦接触对。在流体介质为水的情况下，金属摩擦副的摩擦因数通常在0.1～0.3之间，文中分析时摩擦因数选择为0.15[10]。密封环在工作中因压缩和超高压会使网格严重扭曲，因此模型采用减缩积分单元CAX4R网格。

图2所示为密封件的压缩回弹加载过程和压缩加压的密封过程。

图2 C形密封环不同加载情况

如图2(b)所示，密封过程分为压缩和加压这2个阶段：加载时，上刚性面整体向下压缩，该过程模拟密封圈的初始密封状态；加压时，将170 MPa压力逐渐加载至C形密封环，该过程模拟C形密封环受到超高水压的密封状态。

2 有限元结果及分析

2.1 有限元模型验证

压缩回弹特性是衡量C形环力学性能的重要指标之一，也是验证模型正确性的重要方法。对无银层和有银层C形密封环分别施加1.05和1.10 mm的压缩量，以保证两者在压缩阶段有相同的压缩率[7]，并选取实验数据[2]进行压缩回弹特性对比。处理有限元仿真结果，可以得到如图3所示的C 形密封环的压缩回弹曲线。

图3 有银层和无银层C形密封环压缩回弹结果比较

由图3可知：有银层和无银层的2条模拟曲线变化规律基本一致，这表明银层对C形密封环的压缩特性没有实质性影响。对比模拟曲线和实验曲线可知：仿真结果与实验具有一致性，验证了理论模型的正确性，因此有限元模型可以进行简化。

2.2 定常动态分析

C形密封环依靠与筒体的变形实现密封，所以研究密封组件的接触应力分布是密封分析中的重要一环。为研究万米深海高压舱的超高压密封问题，选取压力170 MPa为定常压力参数，并以压缩回弹分析中1.05 mm的压缩量为定常压缩参数，研究在各阶段的动态密封情况。

由图4可以看出：压缩阶段时，接触应力先上升而后缓慢下降，压缩量过小则接触应力较小，无法满足进入加压阶段时的密封要求，压缩量较大时，接触应力减小；在加压阶段，接触应力先下降后上升，这是因为随着压力的增加，压力在使密封环起自紧作用的同时，有一部分压力充当了开启力，当工作压力增加到一定的值时，接触压力达到最小值，密封环发生了径向移动，同时密封环的接触应力均远大于密封所需的基准值，可以保证良好的密封性能。由此可以看出压缩量和外压值在很大程度上能影响密封环的密封性能。

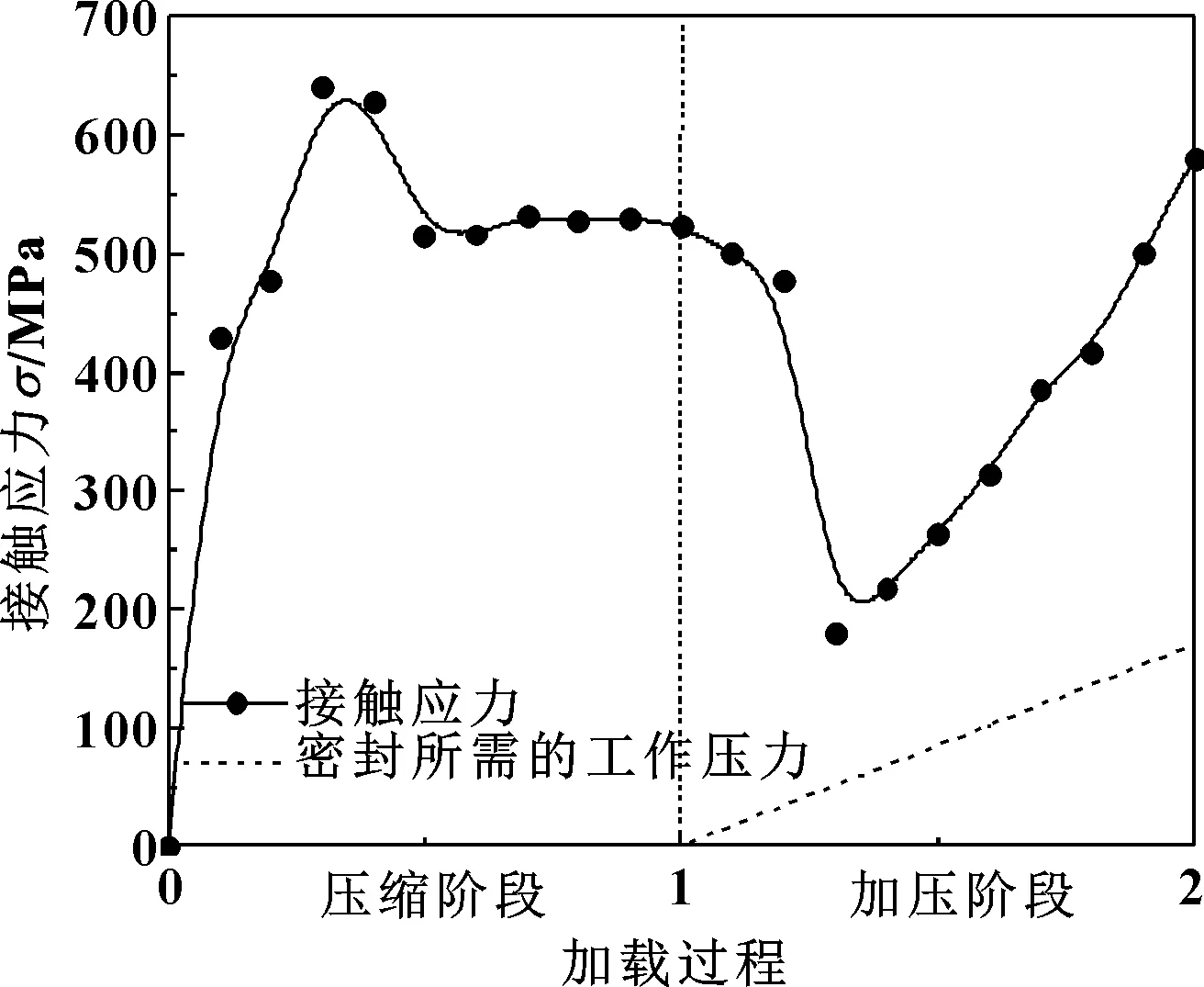
图4 压缩阶段和加压阶段接触应力

2.3 压缩量对密封性能的影响

压缩量对于密封环能否实现密封有重要的影响，若初始压缩量过小，密封环不足以填塞密封面的变形和表面粗糙度，在微观上就会形成界面泄漏的微小通道，压缩量过大，大到一定的程度密封环会发生塌陷，失去回弹性能，引起密封失效[11-12]。

图5示出了不同压缩量下C形密封环最大Mises应力分布。可以看出：包覆层的最大Mises应力先减小，在压缩量为0.65 mm时，应力达到最小值，而后随着压缩量增大，应力随之增加；弹簧层最大Mises应力随压缩量增加呈线性增加，在压缩量小于0.85 mm时最大Mises应力小于屈服强度，可保证密封件的安全性。

图5 不同压缩量下最大Mises应力分布

图6示出了不同压缩量下最大塑性应变分布。随着压缩量增大，包覆层和弹簧层最大等效塑性应变缓慢增加，压缩量为0.85 mm时，应变曲线斜率增大，因此压缩量过大会加速材料塑性硬化。比较包覆层和弹簧层在同一压缩量下的应变值，可以看出，密封过程中包覆层产生的塑性变形量较大，较弹簧层更易发生破坏。

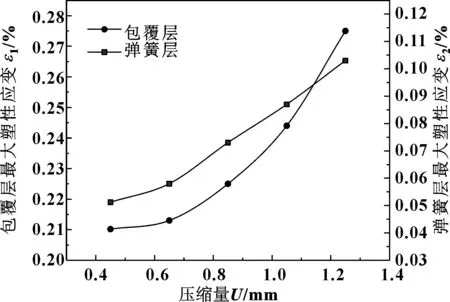
图6 不同压缩量下最大塑性应变分布

加压完成后选取图7中C形环路径并提取接触应力分布数据，得到密封环的接触应力分布图。可知：接触宽度随压缩量的增长而增加，并分布均匀；接触应力分布在450～780 MPa范围内，远大于工作压力(170 MPa)具有优良的密封性能。

图7 不同压缩量下接触应力分布曲线

综上，压缩量过低，包覆层与刚体接触面积较小，施加外压后会产生应力集中从而导致包覆层损坏；压缩量过高，弹簧层受到的轴向载荷过大，等效应力过高会引起失效；包覆层塑性变形较大，更易损坏；不同压缩量下接触应力远大于工作压力，C形密封环具有良好的密封性能。

2.4 外压对密封性能的影响

取压缩量为1.05 mm，分析外压在90～190 MPa范围内变化时C形密封环的密封性能变化情况。

图8给出了包覆层和弹簧层在不同外压作用下的最大Mises应力曲线。可以看出：包覆层等效应力曲线变化平缓，基本不随外压变化而变化，其最大Mises应力稳定在680 MPa，接近极限强度；弹簧层等效应力曲线随外压增加呈线性增长，皆小于极限强度，若外压持续增加弹簧层的最大等效应力将随之增加，会造成弹簧层损坏。

图8 不同外压下包覆层与弹簧层最大Mises应力

选取如图7所示路径并提取数据，得到如图9所示的不同外压作用下密封环的接触应力分布。可知：接触宽度稳定在1.75～2.15 mm之间且分布均匀；最大接触应力在330～620 MPa范围内，远大于工作压力；外压增大，接触应力也随之增加，可以满足超高压密封要求；由于外压的推动作用，最大接触应力点分布在中间位置偏右侧。

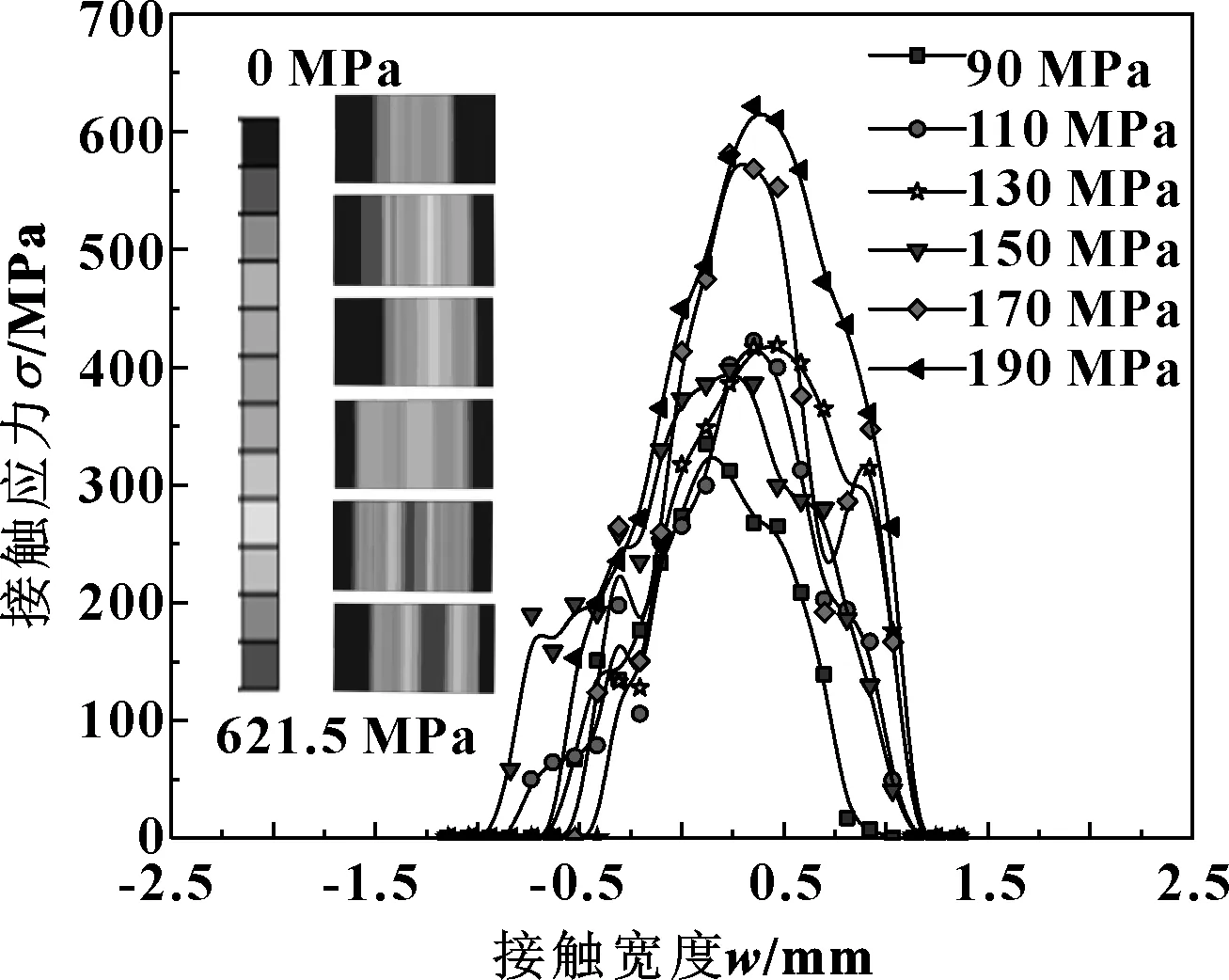
图9 不同外压下C形环接触应力分布

综上，外压对密封环的安全性能有一定的影响，过高外压会使材料损坏从而导致密封失效，但可以提高最大接触应力值以满足严苛的密封要求。

3 结论

(1)利用有限元软件Abaqus建立C形密封环的二维轴对称模型并进行仿真。结果表明：银层和无银层密封环模型的压缩回弹特性结果吻合，表明银层对C形密封环的压缩特性影响较小；模拟结果与试验数据相近，验证了无银层的C形密封环模型准确性。

(2)对密封环在定常条件下接触特性分析表明，在加压阶段，由于密封环发生了径向移动，一部分压力充当开启力，接触应力先减小后增加；在170 MPa超高压环境下接触应力远大于工作压力，可以满足超高压密封要求。

(3)外压为定值、压缩量增加时，压缩量过低，包覆层与刚体接触面积较小，施加外压后会产生应力集中从而导致包覆层损坏；压缩量过高，弹簧层受到轴向载荷过大，等效应力过高会引起失效；包覆层塑性变形较大，更易损坏；不同压缩量下接触应力远大于工作压力，C形密封环具有良好的密封性能。

(4)压缩量为定值、外压值增大时，包覆层最大Mises应力基本稳定在接近极限强度值，而弹簧层最大Mises应力随外压增大而增大；最大接触应力呈线性增加，可以保证良好的密封特性。