螺杆定子衬套热老化本构参数及内腔变形规律研究*

(西南石油大学机电工程学院 四川成都 610500)

螺杆钻具(Positive Displacement Motor，PDM)作为石油天然气开采中的主要动力工具之一，在我国年使用量超过2万套[1]。但螺杆钻具电动机在工作超过100 h后，其机械效率往往会从50%下降到35%左右，在深井高温环境中更是如此，其性能衰退的主要原因是定子橡胶的热老化[2]。目前国内外关于螺杆钻具定子橡胶力学性能的研究已有一定的进展，但是关于深井高温环境下定子衬套材料氢化丁腈橡胶力学性能的研究还不充分。随着我国深井、超深井钻探数量的增多，亟需研究深井高温环境下衬套橡胶热老化过程中的力学性能变化，以及对螺杆钻具定子衬套线型变形规律的影响。

国内外学者的研究表明，橡胶的热老化过程实际上是高分子材料发生化学交联的过程，交联度和交联密度随着温度的升高及老化时间的增加而变化，它们共同影响着橡胶硬度及其力学性质的变化[3]。叶卫东等[4]利用经验公式得到Mooney-Rivlin模型参数，模拟了橡胶材料力学参数对螺杆泵密封性能的影响。WOO等[5-6]基于单轴拉伸试验和等双轴拉伸试验研究了天然橡胶的力学性能，预测了天然橡胶的寿命。王明起[7]总结了橡胶力学性能试验的相关方法，提出了橡胶定子疲劳寿命预测方法。曹婷婷[8]进行了密封圈橡胶材料老化试验，并建立了相关的有限元模型。文献[9-11]对橡胶疲劳特性和螺杆泵结构参数开展了研究。然而，目前学者对石油装备中螺杆钻具定子橡胶衬套的系统研究仍较少，对螺杆钻具力学性能研究的相关文献也不多。

本文作者基于ASTM材料试验标准，制备螺杆钻具定子衬套采用的氢化丁腈橡胶试样，并进行热老化处理及拉伸试验；基于Mooney-Rivlin模型和Yeoh模型理论拟合了本构模型参数；建立了定子衬套有限元模型，并模拟了不同井深下的定子衬套变形规律。

1 橡胶本构模型及参数拟合

目前橡胶材料超弹性本构模型种类较多，文中仅讨论在工程计算中应用较多且在各应变区间计算精度不同的Mooney-Rivlin和Yeoh 2种本构模型。

1.1 Mooney-Rivlin模型

该模型假设橡胶材料应变能密度W可以分解为应变偏量能和体积应变能两部分，在未变形状态下其弹性是各向同性的，且完全不可压缩的，那么W的函数形式如下：

(1)

式中:Cij(C00=0)为常数;I1为第一应变不变量;I2为第二应变不变量;I1、I2和第三应变不变量I3与3个方向的主拉伸比λ1、λ2、λ3关系如下：

(2)

按Mooney-Rivlin模型的常用简化形式能够将硫化橡胶应变能W表示为

(3)

对于不可压缩的橡胶材料，I3=1。橡胶材料主应力τi与其主生长比λ之间的关系为

(4)

在单轴拉伸试验中，上式中τ2=τ3=0，可得到：

(5)

并且应力差关系如下:

(6)

不难发现式(6)中的偏导式可由式(1)两边分别对I1、I2求偏导得到，并能得到如下结论：

(7)

将式(7)代入式(6)中可以获得如下关系:

(8)

在力学中，真实应力τ与实际应力σ有如下关系：

τ=λσ

(9)

最后使用工程应力代替实际应力，获得工程应力和工程应变的关系：

(10)

利用式(10)确定C1、C2的方法为：以1/λ为横坐标，以σ/[2(λ-1/λ2)]为纵坐标，将试验得到的数据拟合为一条直线，该直线截距即为C1，斜率即为C2。

1.2 Yeoh模型

在研究橡胶材料应力应变关系的过程中，Yeoh模型对单轴拉伸应力与应变之间的关系进行了一定的简化，使用了一个3次应变能函数来描述这种关系：

(11)

式中:N一般为3，即为三次应变能函数；对于橡胶类不可压缩材料，J取值为1；Ci0为Yeoh模型系数。

因此上式等号右边可以省略一半，对W求I1、I2的偏导，可得下式：

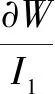
(12)

由于都是单轴拉伸试验，将式(12)代入式(8)可得到τ与I的关系，再由式(2)获得I与λ的关系，最后用式(9)将τ转化为σ，获得σ与λ的关系式如下：

(13)

式(13)即最后用于Yeoh模型的试验数据处理公式。利用式(13)确定C10、C20和C30的方法为：以(λ2+2/λ-3)为横坐标，以σ/[2(λ-1/λ2)]为纵坐标，拟合出一条二次曲线，C10即最低点(最高点)的纵坐标，C20即1/2一次项系数,C30即1/3二次项系数。

1.3 橡胶热老化试验及本构模型参数拟合

试验用氢化丁腈橡胶试样、老化试验箱和橡胶拉伸试验仪如图1所示。

图1 试验试样及设备

按照ASTM标准，将氢化丁腈橡胶试样放置于老化试验箱内，分别在70、100、130、150 ℃温度下进行热老化处理，然后在橡胶拉伸试验仪上进行拉伸试验，得到橡胶试样的工程应力-工程应变数据。每种试验条件下重复5次试验，取平均值。

按照橡胶本构模型理论中的应力-应变处理方式，计算出Mooney-Rivlin模型数个横纵坐标点，并拟合直线，结果如图2所示。

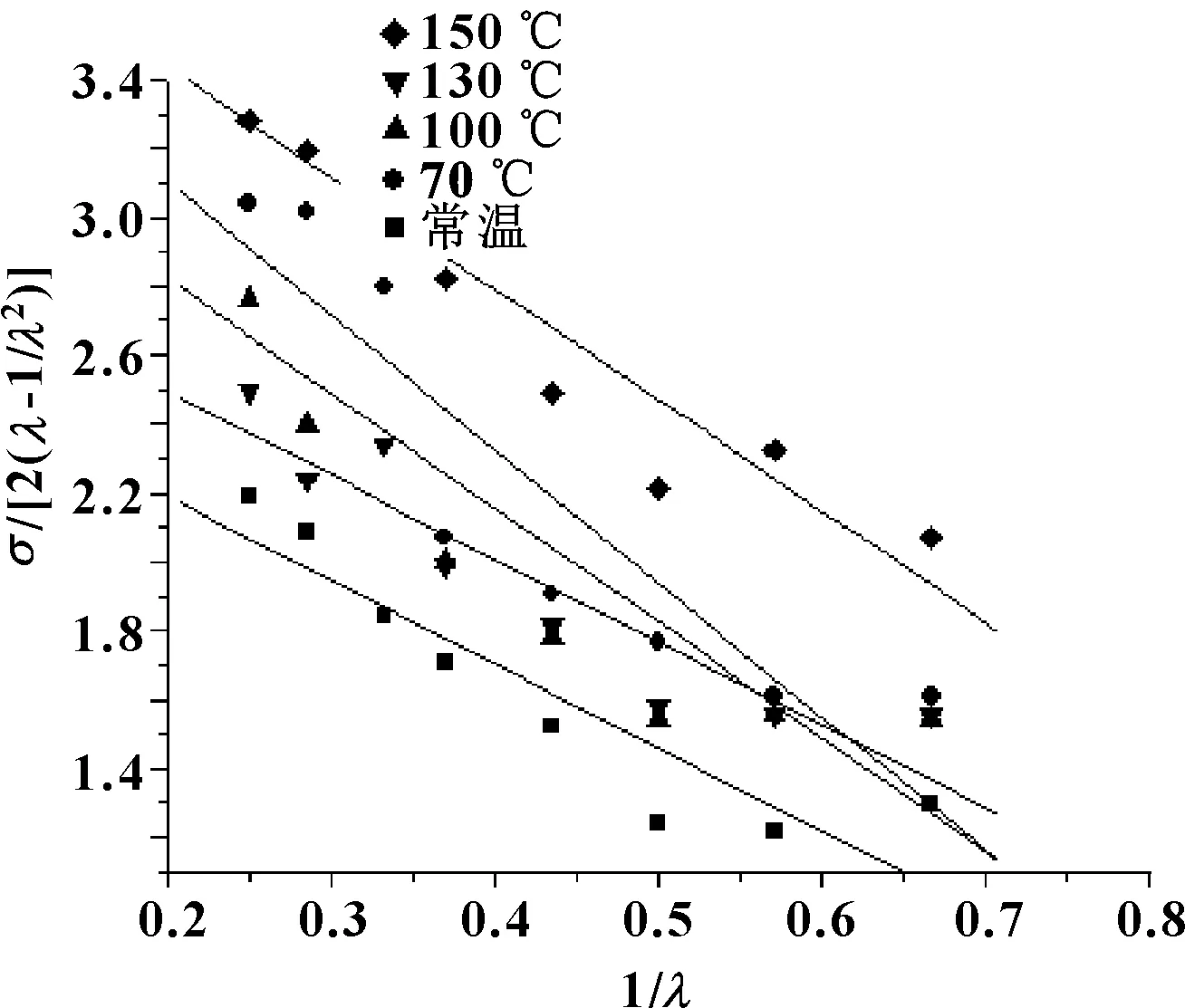
图2 Mooney-Rivlin模型的拟合直线

图2中拟合直线的截距即为Mooney-Rivlin模型参数C1，直线斜率即为模型参数C2。不同温度下氢化丁腈橡胶Mooney-Rivlin模型参数如表1所示。可以看出，Mooney-Rivlin模型的参数C1、C2随着温度增加均表现出先减小后增大的变化趋势。

表1 不同温度下氢化丁腈橡胶Mooney-Rivlin模型参数

Yeoh模型横纵坐标点计算方法同上，对得到的散点拟合二次曲线，结果如图3所示。

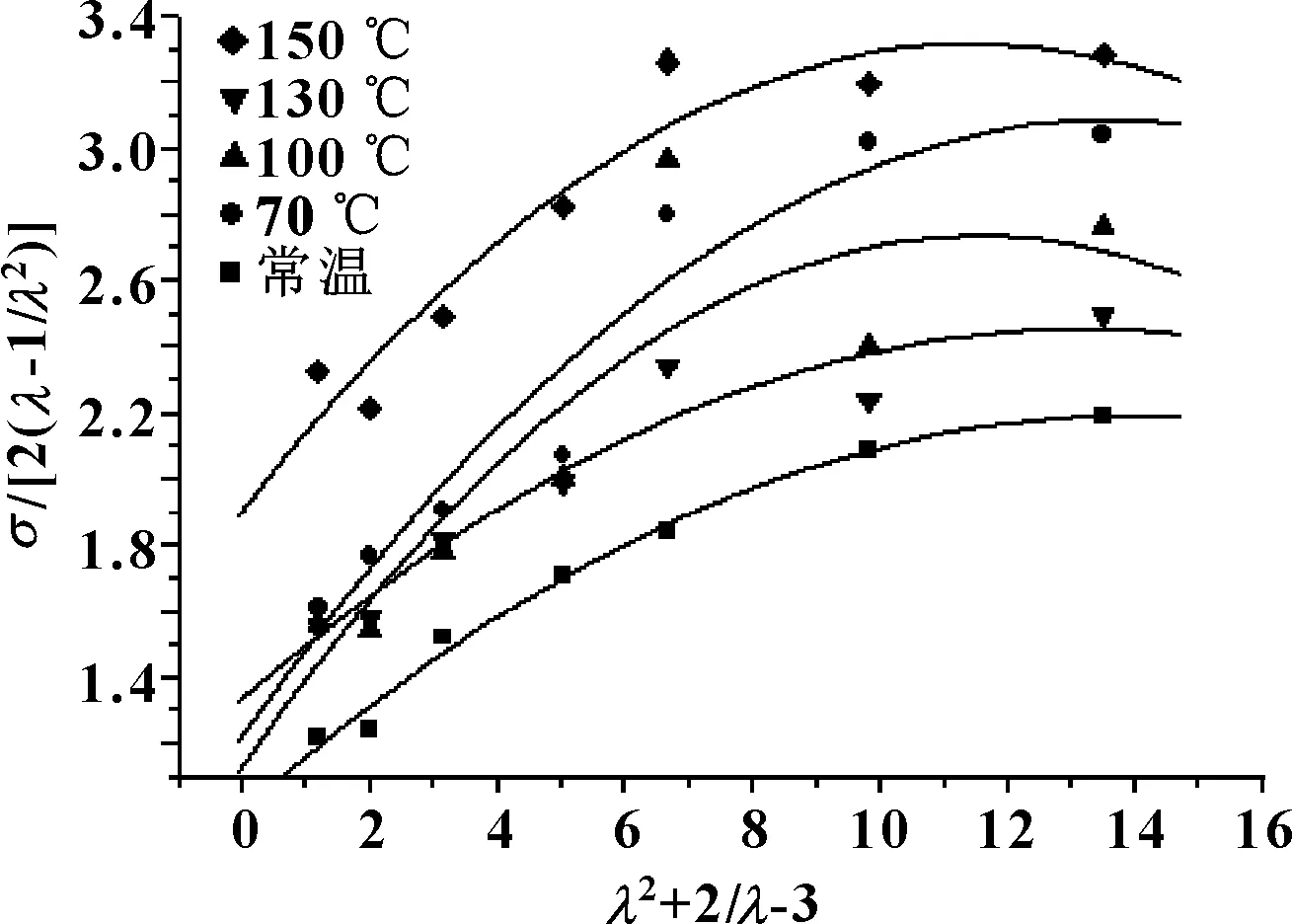
图3 Yeoh模型的拟合二次曲线

Yeoh模型参数可由图3所示曲线获得，取拟合曲线最低点(或最高点)的纵坐标为参数C10，一次项系数的1/2为参数C20,二次项系数的1/3为参数C30，得到的不同温度下氢化丁腈橡胶Mooney-Rivlin模型参数如表2所示。可以看出，随温度升高Yeoh模型参数C10、C20均呈现出先增加后减小再增加的波浪形趋势，而参数C30则相反。

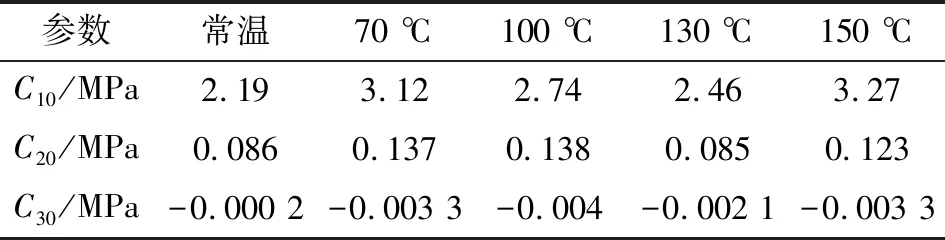
表2 不同温度下氢化丁腈橡胶Yeoh模型参数

2 Mooney-Rivlin和Yeoh模型参数拟合精度评价

深井高温环境下螺杆钻具定子衬套橡胶本构关系的恰当选取及其模型参数拟合精度的正确评价是保证有限元计算结果准确的关键。

2.1 本构模型参数拟合精度评价方法

对式(1)中的势能函数W在单轴拉伸状态下的拉伸率求导，可求得该状态理论工程应力。如式(14)所示。

(14)

式中：λ为单轴拉伸的拉伸率；σ为理论工程应力；W为应变能函数；I1、I2分别为第一、二应变不变量。

式(14)中应变不变量I1、I2由下式计算：

(15)

本构模型的拟合精度由式(16)计算。

(16)

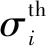
将所测量的单轴拉伸的应力-应变数据代入式(14)、(15)、(16)可计算出Mooney-Rivlin模型以及Yeoh模型拟合精度。具体计算结果如表3所示。可以看出：两本构模型的误差随温度升高均表现出先增大后减小的趋势，均在130 ℃达到误差最大值；不同温度下Yeoh模型的误差均比Mooney-Rivlin模型的误差小，因此，对于橡胶超弹性材料，Yeoh模型的计算精度优于Mooney-Rivlin模型。

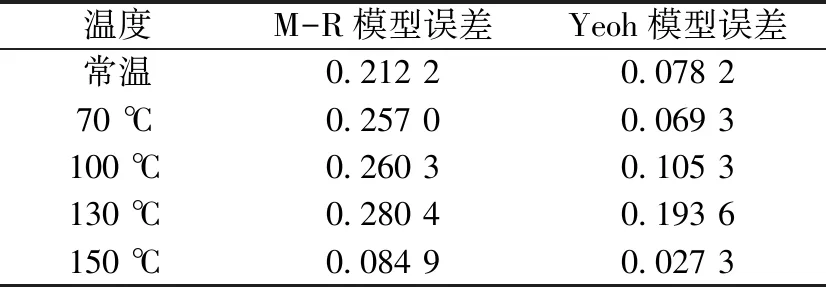
表3 氢化丁腈橡胶Mooney-Rivlin和Yeoh模型拟合误差

2.2 本构模型参数拟合精度校核

为检验2种本构模型拟合精度，通过仿真分析研究了最贴近真实的螺杆电动机定子橡胶变形。建立的有哑铃型有限元模型如图4所示。将模型左端边界设置为全约束，右端施加位移条件，分别设置材料属性为Mooney-Rivlin和Yeoh模型参数。考虑到温度跨度较大，因此进行常温和130 ℃两组仿真。设置应变条件，获得了两组温度下的应力数值，如图5所示。可见，Yeoh模型比Mooney-Rivlin更能反映实际情况。

图4 哑铃型试片仿真模型

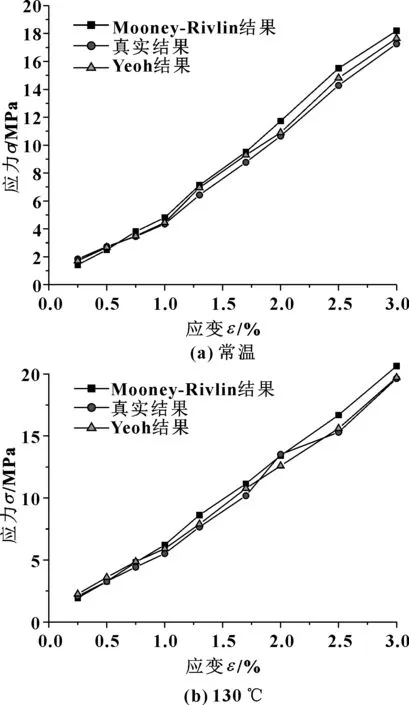
图5 Yeoh模型和Mooney-Rivlin模型仿真结果

综合本构模型参数拟合精度的评价和校核结果，确定Yeoh模型能更真实地反映氢化丁腈橡胶的力学特性。

3 橡胶热老化本构参数对定子衬套内腔变形规律研究

以国内应用较为广泛的5/6头螺杆钻具定子衬套为研究对象，开展仿真研究。有限元模型如图6所示，该模型外壳体为φ172 mm，橡胶衬套内壁等距圆半径R=13.2 mm，偏心距e=7.99 mm。文献[12]采用三维螺杆电动机模型进行了力学性能有限元分析，对比相同条件二维模型的分析结果，发现两者差距很小。因三维模型运算量较大，因此文中使用二维螺杆电动机定子衬套模型研究内腔变形规律。

图6 定子衬套仿真模型

为了模拟螺杆电动机在井下的工作环境，设置该定子的外侧边界为全约束,在螺杆电动机定子衬套内部施加均匀压力，压力数值根据螺杆钻具所在井深和地层压力梯度计算确定。

根据经验公式，取井下地温梯度为每2.113 ℃/100 m。试验中，橡胶拉伸试验温度70、100、130和150 ℃可以对应井下深度2 460、3 880、5 300和6 246 m。钻井液密度为1 200 kg/m3，按液体压力公式p=ρgh计算内腔壁压力，得到4个温度下对应的内腔压力为27.1、44.7、62.3和74.1 MPa。

定子真实位移数据采集路径如图7所示，由内壁上方中央开始顺时针逐一选点绕内壁一周，常规定子和等壁厚定子路径相同。图8、9分别示出了考虑和不考虑老化时常规定子和等壁厚定子在4种井深条件下的真实位移。可见：在同一井深条件下，无论是常规定子还是等壁厚定子，不考虑老化(使用常温下氢化丁腈橡胶Yeoh模型参数)的真实位移比考虑老化时的真实位移要大，并且随着温度的增加，这个差值表现出先增大后稳定再增大的趋势，差值在6 246 m井深时甚至达到了70%。由此说明，在仿真分析时应考虑老化因素的影响。

图7 截面路径典型点

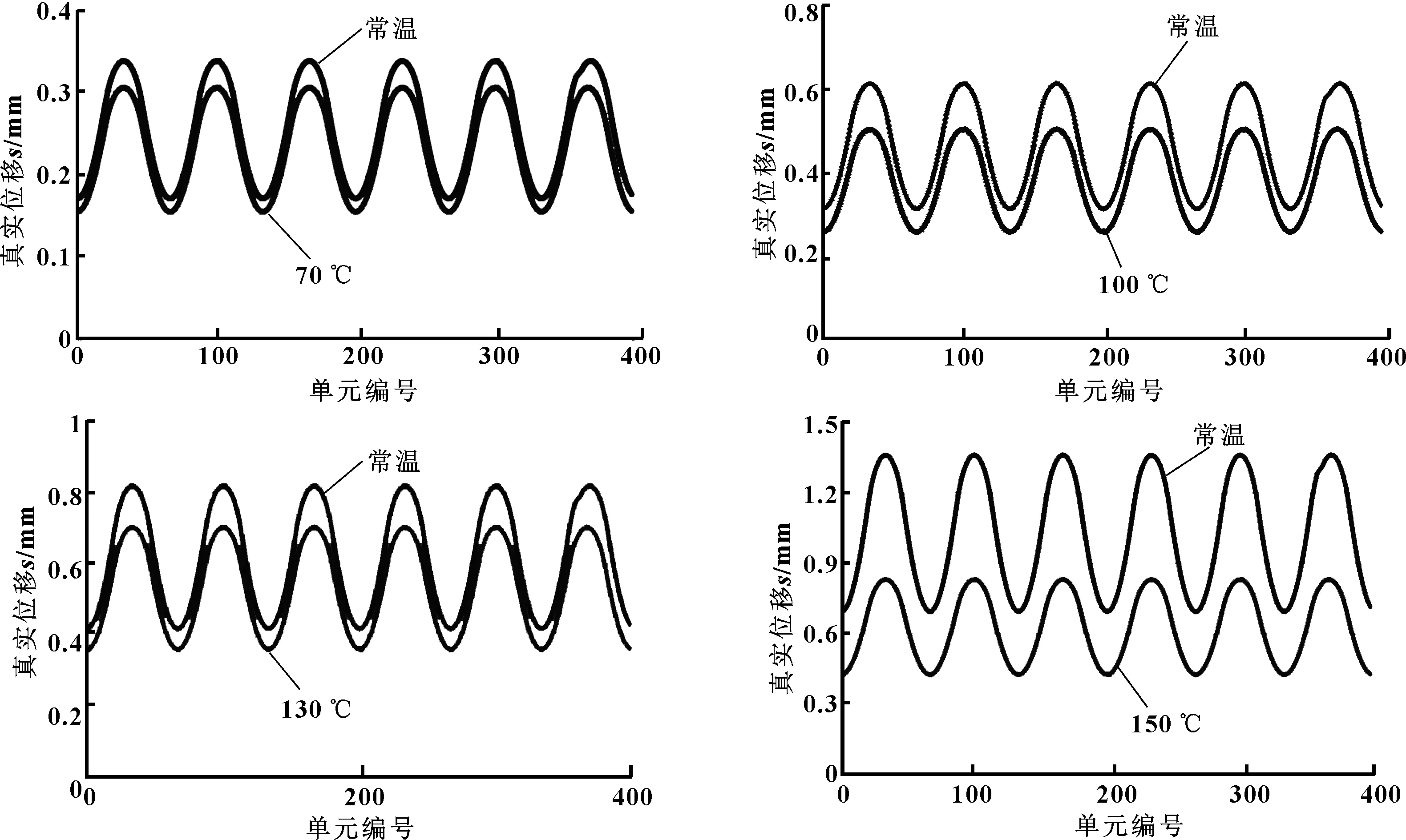
图8 考虑和不考虑老化时不同井深下常规定子的真实位移

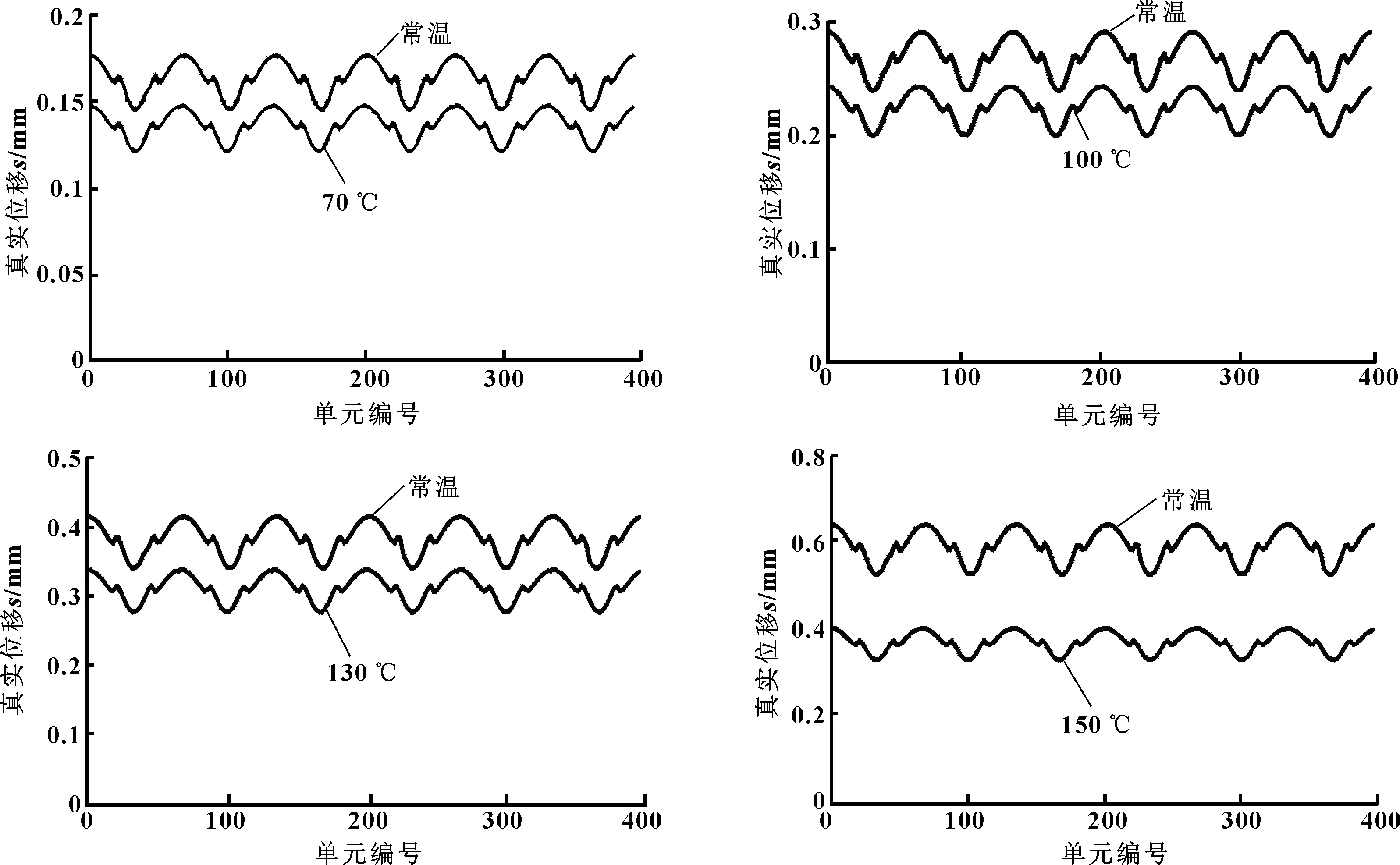
图9 考虑和不考虑老化时不同井深下等壁厚定子的真实位移

常规定子和等壁厚定子的真实位移最大值、最小值位置几乎完全相反，如何综合2种定子结构使运动更平稳以延长螺杆钻具的使用寿命将成为一个研究方向。

图10比较了不同井深下定子的真实位移。常规定子的真实位移随着井深的增加而增加，位移幅值也随着井深的增加而增加，在6 246 m井深处定子位移幅值比2 460 m井深处增加了170%。等壁厚定子的真实位移同样随着井深的增加而增加，且其位移幅值增长率与常规定子几乎相同。但同温度下常规定子是等壁厚定子的幅值的5倍，等壁厚定子可用较小过盈量满足密封要求，以降低定子衬套磨损，并提高单级承压能力。

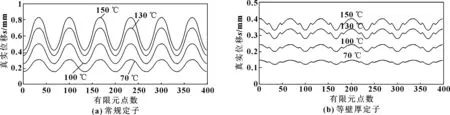
图10 不同井深下定子的真实位移

4 结论

(1)通过热老化和单轴拉伸试验，获得了氢化丁腈橡胶试样不同温度下的本构模型参数。其中Mooney-Rivlin模型的参数C1、C2随着温度增加均先减小后增大；Yeoh模型参数C10、C20均呈现出先增加后减小再增加的波浪形趋势，而参数C30则相反。

(2)利用计算误差评价方法和仿真校核方法比较了2种本构模型参数拟合精度，最终确定Yeoh模型更能真实地反映氢化丁腈橡胶的力学性能。

(3)无论常规定子还是等壁厚定子，随着井深的增加，常温本构模型与热老化本构模型的差值不断增加，因此在仿真分析时应考虑老化因素的影响。

(4)相同温度下常规定子的位移幅值是等壁厚定子的5倍，等壁厚定子可用较小过盈量满足密封要求，以降低定子衬套磨损，并提高单级承压能力。

(5)对于螺杆钻具电动机的后续研究，可基于深井高温环境，建立螺杆钻具电动机热-机耦合三维动力学模型和数值模拟方法，进一步揭示电动机工作效率衰退及漏失机制，为合理选择定子衬套橡胶材料、匹配螺杆钻具定转子结构参数及线型优化设计提供理论基础。