响应曲面法优化封隔器胶筒密封性能参数的研究*

(天津科技大学机械工程学院，天津市轻工与食品工程机械装备集成设计与在线监控重点实验室 天津 300222)

封隔器胶筒是油气勘探时压裂用封隔器的关键部件，利用径向膨胀时胶筒与套管壁之间产生的接触压力起密封作用[1]。 胶筒的密封性能对提高压裂用封隔器的工作性能和保证分层开采工艺的有效实施具有重要意义。胶筒的密封能力取决于弹性胶筒在轴向工作载荷作用下，外径受限约束时的径向扩张变形情况，而胶筒的变形与胶筒的结构参数、材料参数、工况参数等相关。特定工况下某种材料的胶筒，施加工作载荷时，胶筒的变形主要依赖于胶筒筒高、端面斜角、胶筒的厚度及子厚度等结构参数，每一个结构参数的改变都会使胶筒的变形发生变化，从而影响胶筒与套管间的接触压力。因此，研究胶筒与套管之间的接触压力与胶筒结构参数之间的定量关系非常重要。

胶筒变形过程的几何、材料及状态的非线性，给理论研究带来很大难度，加之实验研究的耗时和昂贵，因此，封隔器胶筒的密封性能主要通过有限元模拟仿真研究。周先军等[1]利用有限元对3种胶筒接触应力进行分析，得到了接触应力沿胶筒轴向的分布情况。文献[2-4]在利用有限元软件对常用的三胶筒结构进行密封性能分析的基础上，提出了胶筒的改进设计方案。吴晋霞等[5]利用有限元软件分析了胶筒厚度、端面斜角和材料特性结构参数对胶筒密封的影响，并提出了胶筒的改进设计方案。刘永辉等[6]通过分析端面斜角和筒高对胶筒接触应力的影响，确定了胶筒合理的结构参数。在数值模拟计算方面，AL-HIDDABI等[7]基于压力法建立了扩张型胶筒密封的闭式解求解模型，并分析了胶筒的压缩率、胶筒壁厚、材料特性对胶筒密封性能的影响；HU等[8]通过建立胶筒材料的有限元模型，分析了不同壁厚和不同工作压差下，不同胶筒材料对密封性能的影响；仝少凯[9]建立了胶筒坐封过程中的力学模型，分析了其坐封状态时的接触应力大小，并研究了胶筒的密封性能。但现有胶筒密封性能的研究，仅研究了单一结构参数变化对胶筒密封性能的影响，忽略了参数间的交互作用。事实上，胶筒的密封性能是在多参数相互作用下实现的。

响应曲面法[10](Response Surface Methodology，RSM)是指通过合理安排实验和分析实验数据，以获得使响应变量达到最优化的各因子最佳水平范围的数理统计方法。为了研究和优化胶筒密封性能的结构参数，本文作者首先利用有限元分析软件，分析了胶筒单因子结构参数对最大接触应力的影响；然后利用有限元分析的结果，通过响应曲面法实验，研究了多因子不同水平下胶筒最大接触压力响应的变化情况；最后建立了不同胶筒结构参数下，反映胶筒密封能力的最大接触压力预测模型，并给出了实现最大接触压力的胶筒各结构参数的最佳组合方案。

1 胶筒密封结构及模型建立

1.1 胶筒密封的结构及参数

以某型号封隔器的压缩式密封胶筒为研究对象(如图1所示)，其结构和参数如图2所示。

图1 压缩式封隔器结构图

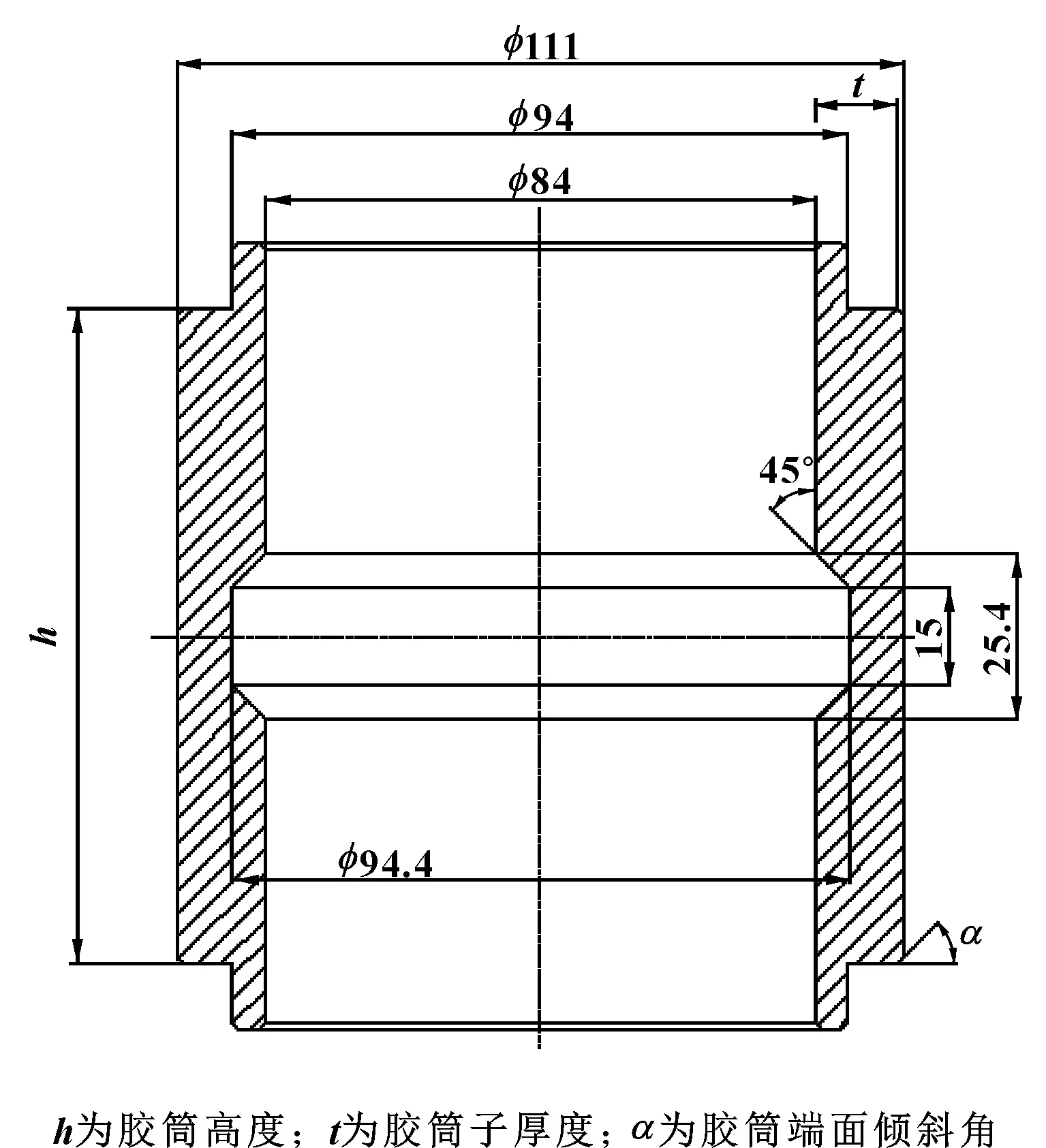
图2 胶筒结构图

1.2 胶筒密封的有限元建模

建立胶筒有限元模型时，其他封隔器零部件，如中心管、支撑环等均采用轴对称单元；胶筒受单向轴向载荷，方向由下压环向上施加，另一端固定。中心管、套管、上下压环和支撑环的材料选择变形量较小的40CrMnMo；而胶筒材料为氢化丁腈橡胶，属于超弹性材料。

超弹性胶筒的材料采用Mooney-Rivlin模型，选国际硬度IRHD为90，经计算模型参数C01=1.925 56 MPa，C10=0.962 8 MPa，弹性模量为17.33 MPa，泊松比为0.499；中心管等其他零部件的弹性模量为206 GPa，密度为7.85 g/cm3，泊松比为0.25。

建立的胶筒二维有限元模型如图3所示，胶筒采用四结点双线性轴对称四边形CAX4RH单元划分网格，而中心管、套管等以CAX4H为单元划分网格。

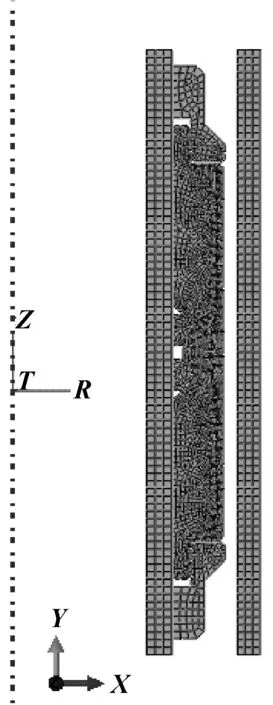
图3 胶筒结构有限元模型

2 胶筒单因子参数对密封性能的影响

封隔器靠管柱压重(或张力)或水力载荷来压缩胶筒，使胶筒封隔环形空间，从而实现密封[11]。有限元分析选取了端面倾斜角、子厚度、筒高和摩擦因数4个因子，分析其对胶筒密封性能的影响。由于胶筒密封属于接触密封，套管壁与胶筒之间的接触应力在一定程度上可以反映胶筒的密封性能。

2.1 端面倾斜角的影响

橡胶属超弹性材料，胶筒在承受较大载荷时，其端面斜角处最容易发生过大变形，即“肩突”，产生应力集中，导致胶筒端部产生裂纹，破损的密封元件会降低密封效果。因此，端面斜角α的优化对提高胶筒与套管间接触应力，减小肩突具有重要作用。

对端面倾斜角为45°的压缩式胶筒施加53.85 MPa轴向载荷(相当于施加42 MPa工作压差)，得到胶筒的主应力分布云图如图4所示。

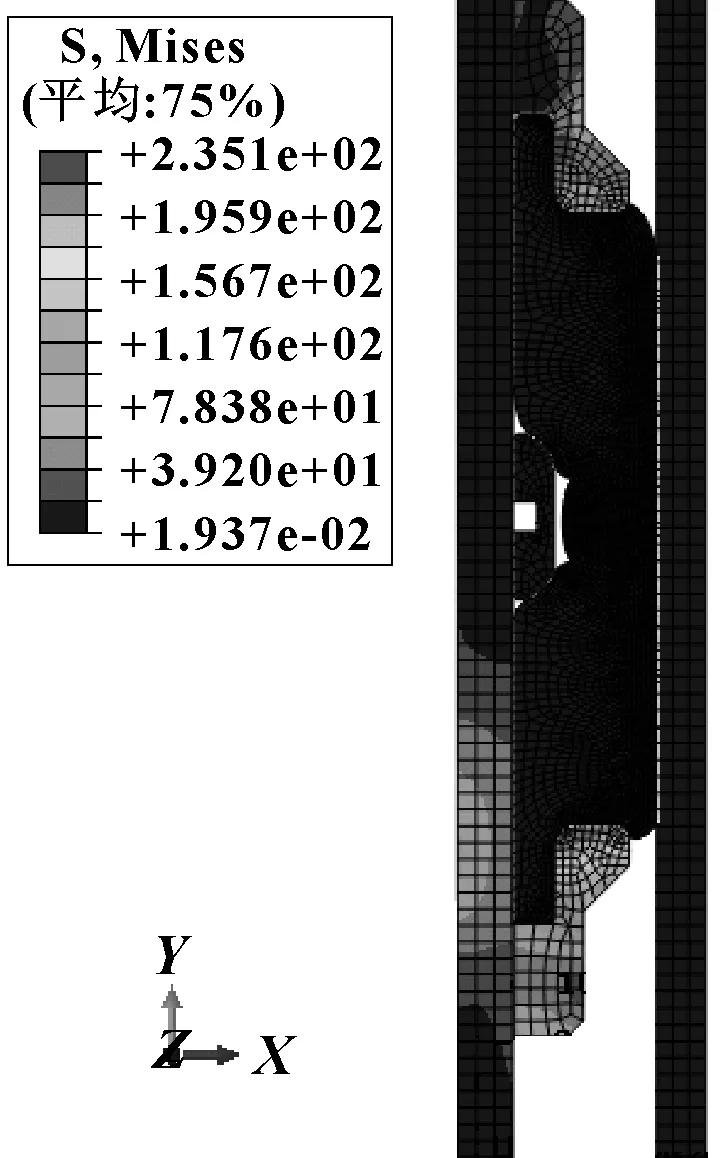
图4 胶筒主应力分布云图(MPa)

为研究端面倾斜角对胶筒与套管最大接触应力的影响，取胶筒端面倾斜角的变化范围为25°～70°，根据有限元分析结果绘制了端面倾斜角与最大接触应力之间的关系图，如图5所示。

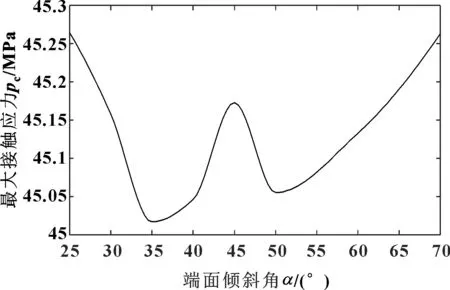
图5 端面斜角与最大接触应力的关系曲线

可见，在其他参数不变的条件下，端面倾斜角度在25°～35°时，最大接触应力随端面倾斜角的增大而减小；在50°～70°时最大接触应力随端面倾斜角的增大而增大；在35°～50°之间，端面角等于45°时获得较高最大接触应力值。

2.2 子厚度的影响

胶筒的子厚度t是胶筒结构的一个重要参数，在不改变胶筒总厚度和端面斜角的前提下，分析胶筒子厚度对胶筒密封性的影响。取子厚度在7.5～12.5 mm范围内变化，经有限元分析得到最大接触应力值与子厚度间的关系曲线，如图6所示。

图6 胶筒子厚度与最大接触应力的关系曲线

从图6可以看出：子厚度在7.5～9 mm范围时最大接触应力随子厚度的增加而增大；在9～10 mm范围时最大接触应力随之减小；但子厚度在大于10 mm后，胶筒与套管的最大接触应力变化不大；当胶筒子厚度为9 mm时，胶筒与套管间的接触应力最大。

2.3 筒高的影响

保持胶筒其他参数不变，仅改变胶筒的筒高h，研究胶筒高度对接触应力的影响。分析得到的胶筒高度在60～160 mm内变化时，与之相应的最大接触应力之间的关系如图7所示。

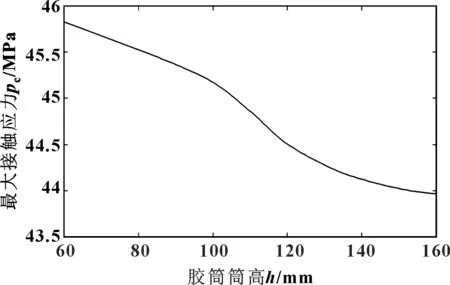
图7 胶筒筒高与最大接触应力间关系曲线

图7表明，在同等轴向载荷作用下，胶筒与套管之间的最大接触应力与胶筒筒高呈单调递减的关系，胶筒高度越高，最大接触应力值越小。

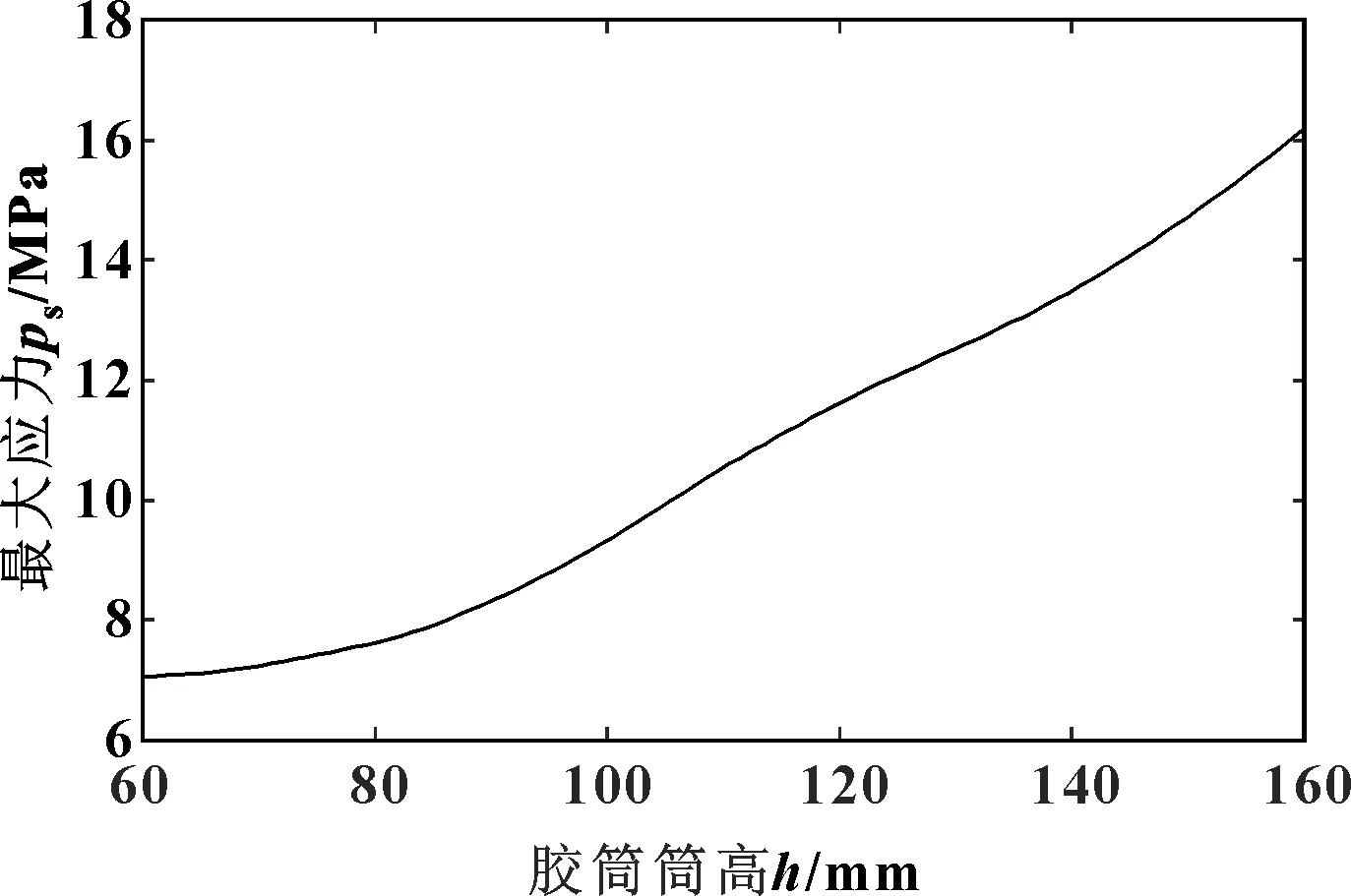
图8 胶筒筒高与应力关系曲线

胶筒筒高与应力值的关系曲线如图8所示，随筒高的增加，胶筒的最大应力值从7.08 MPa快速增长到16.19 MPa，而较大的应力值会加速密封件的损伤，缩短其使用寿命，给安全工作带来隐患。因此，在选择胶筒高度时，要综合考虑胶筒的使用寿命和密封的可靠性。

2.4 摩擦因数的影响

井下工况条件复杂，套管内部有时附着的泥沙、碎屑，以及胶筒的不同材质或中心管的表面形貌等因素，都会影响胶筒与套管等接触面间的摩擦因数，影响胶筒与套管接触处微动时的摩擦力，从而影响胶筒的形变过程及其密封性能。因此，分析摩擦因数对胶筒密封性能的影响是必要的。

建立摩擦分析模型，在模型的相互作用接触属性中调整摩擦因数的变化范围为0.1～0.8，得到的胶筒与套管之间最大的接触应力变化如图9所示。

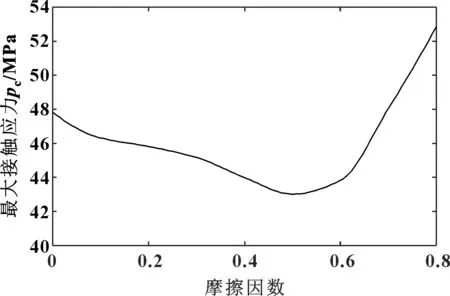
图9 摩擦因数与最大接触应力的关系曲线

从图9可以看出：摩擦因数小于0.5时，胶筒与套管之间的最大接触应力随摩擦因数的增大而缓慢减小；当摩擦因数大于0.5后，接触面之间的摩擦力对胶筒的形变过程产生明显的阻碍作用，使胶筒与套管之间的最大接触应力在摩擦因数大于0.5后急剧增大。

图10所示为不同摩擦因数下胶筒侧面的最大应力分布情况。可见，胶筒侧面的最大应力随摩擦因数增大而增大，较大的摩擦因数会增大胶筒的破损风险。

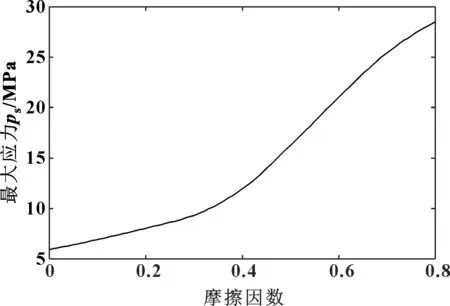
图10 摩擦因数与应力关系曲线

因此，当摩擦因数在0.1～0.3的范围内选取时，可满足胶筒的密封需求，接触应力分布合理。

3 基于响应曲面法的胶筒密封结构参数优化

3.1 影响胶筒密封性能的结构参数

根据有限元分析得到的胶筒端面倾斜角、子厚度、筒高、摩擦因数对密封性能影响的结果，可提取响应曲面设计的分析数据，选取恰当的评价响应的影响因子，其水平如表1所示。并以Box-Behnken试验设计方法对胶筒的密封性能进行试验设计，试验模拟方案如表1所示。

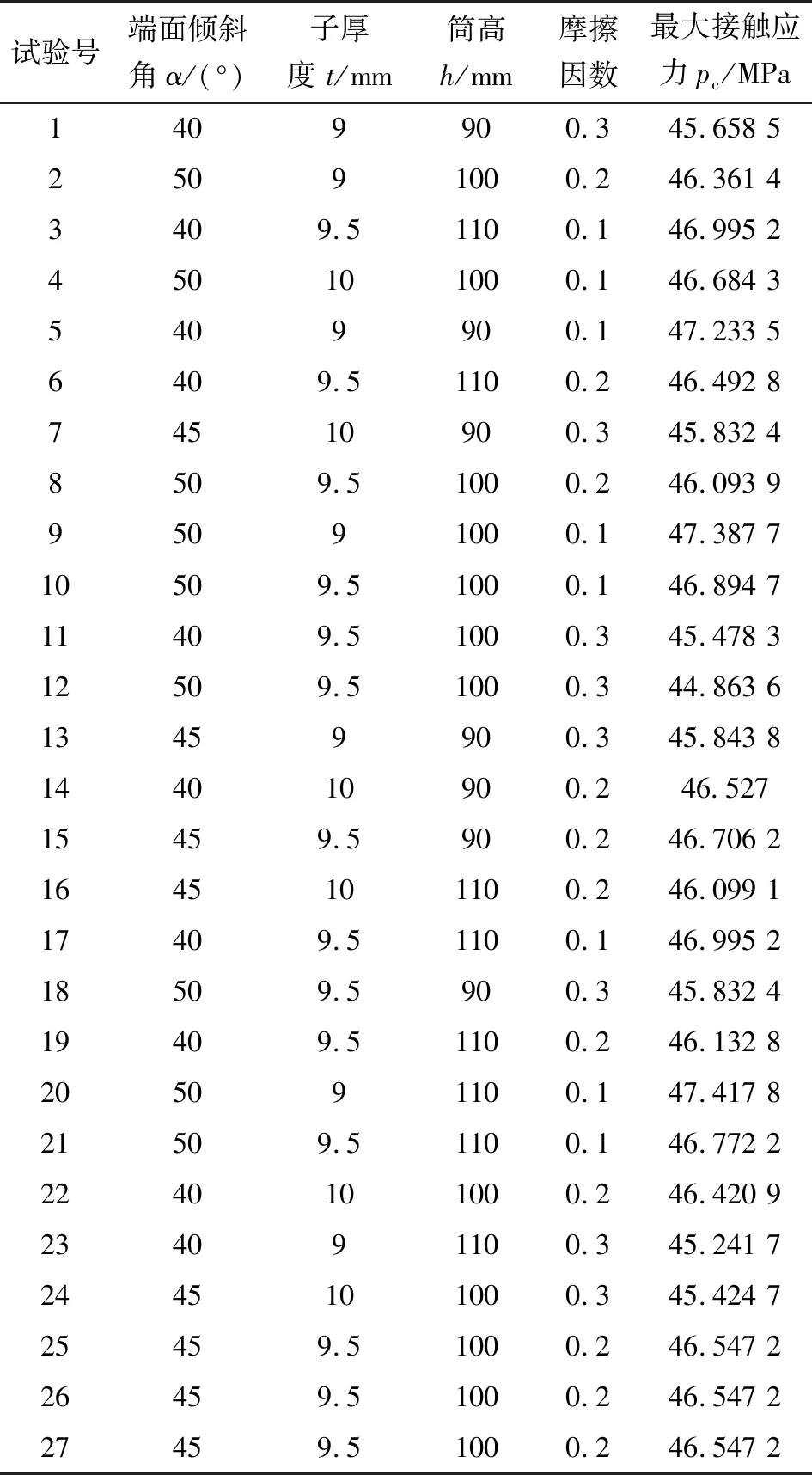
表1 胶筒密封试验设计方案

利用Minitab软件对胶筒密封性能有影响的4个因子作试验设计分析，并将响应数据进行多元拟合，得到胶筒的端面倾斜角(A)、子厚度(B)、筒高(C)、摩擦因数(D)的多元二次回归方程：

Y=30.18+0.87A-1.23B+0.15C-5.84D-0.005 9A2-24.96D2-0.003AC-0.31AD+4.47BD-0.21CD。

表2给出了胶筒最大接触应力方差分析结果。根据回归方程中各项系数及方差分析结果可知，一次项A、B、C、D均对最大接触应力有显著影响，二次项A2、D2和交互项AC、AD、BD、CD对最大接触应力也具有显著性影响。采用田口设计方法研究了4个因子对最大接触应力的影响程度，由表3信噪比的响应分析可知，在所选试验水平范围内，对胶筒最大接触应力影响最大的因子是摩擦因数，最小的是筒高。

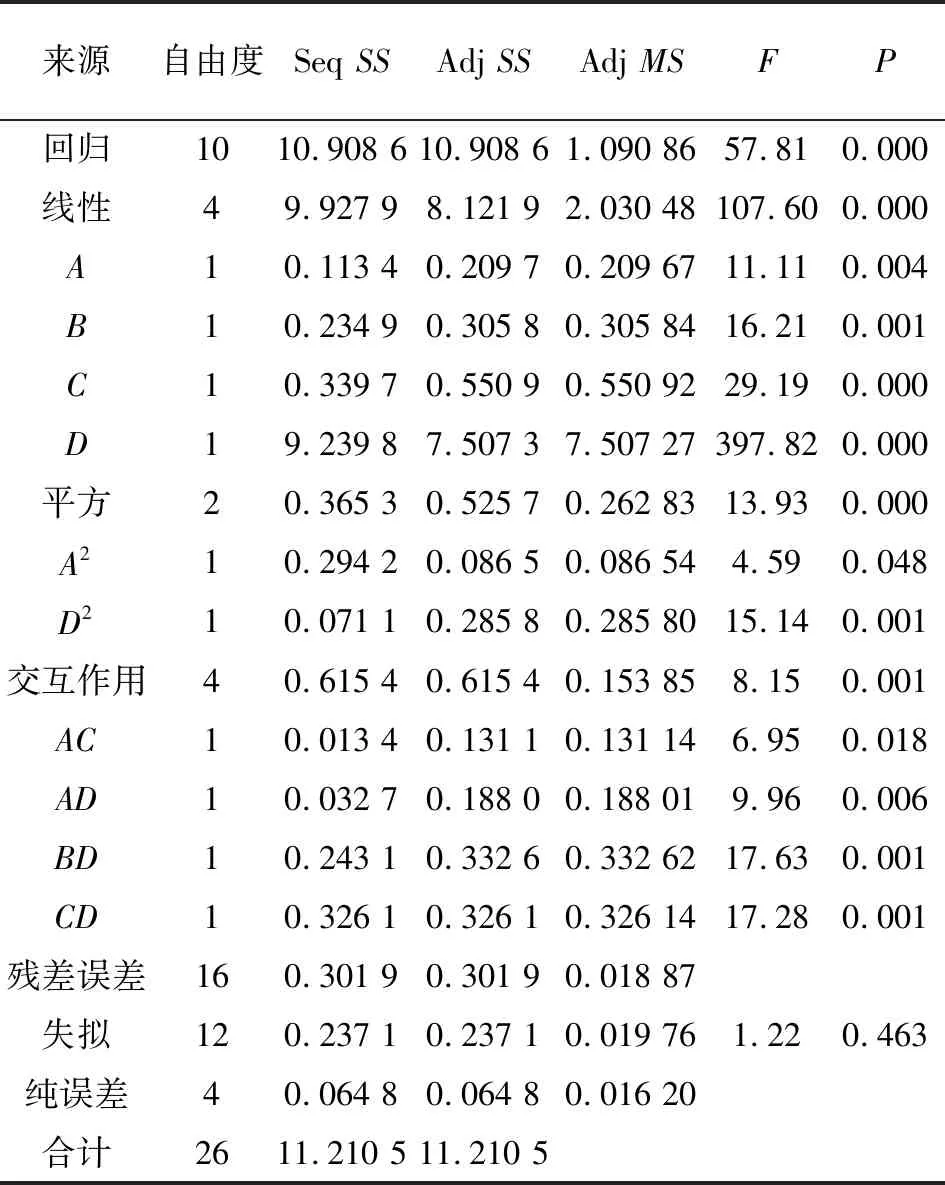
表2 胶筒最大接触应力方差分析表

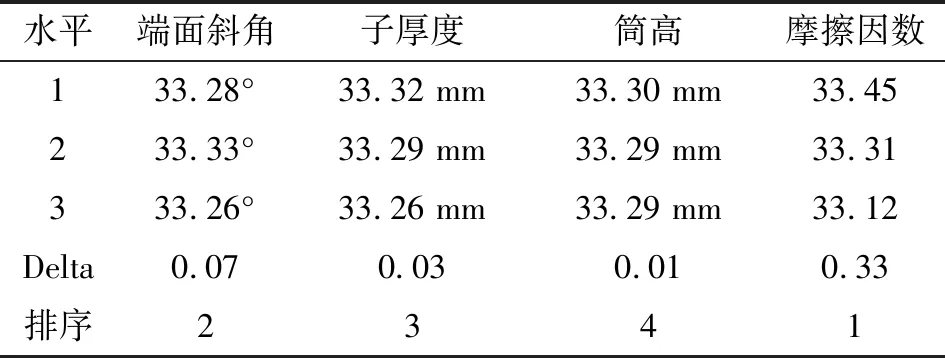
表3 胶筒最大接触应力信噪比响应分析结果

在对该模型简化后的方差分析中(如表2所示)，模型主效应及二因子交互效应P值都小于0.05，因此认为模型是有效的。

3.2 响应曲面结果分析

输出有交互作用因子AC、AD、BD、CD的响应曲面图如图11—14所示。

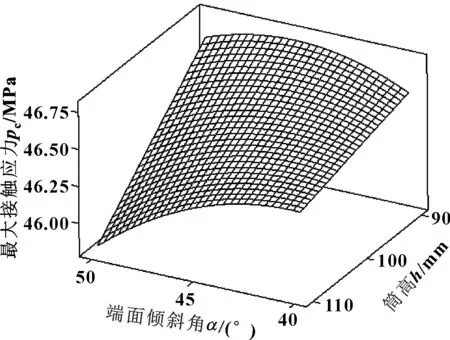
图11 端面倾斜角与筒高对最大接触应力的响应曲面

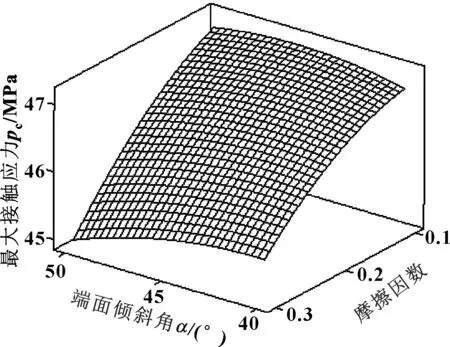
图12 端面倾斜角与摩擦因数对最大接触应力的响应曲面

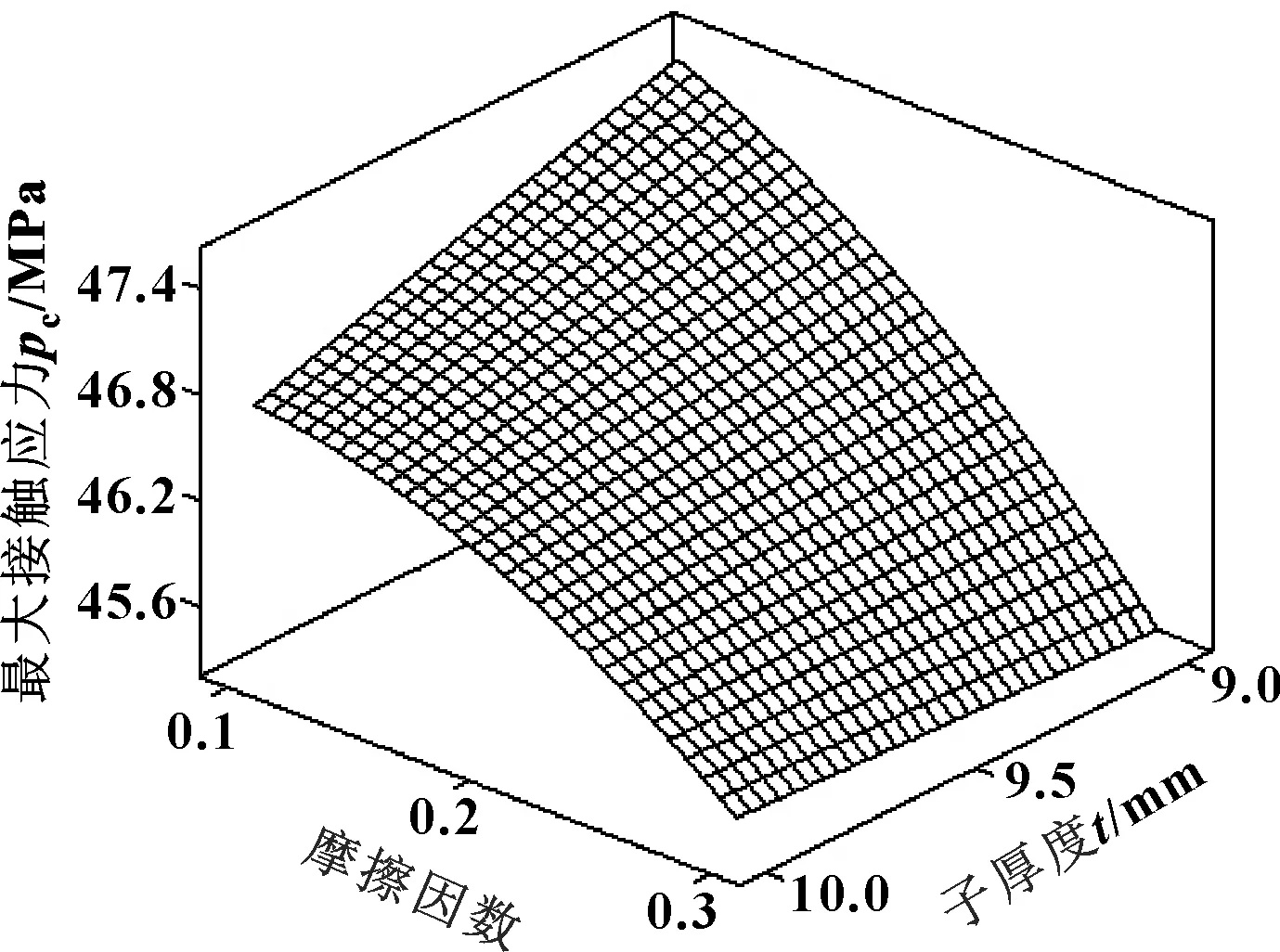
图13 摩擦因数与子厚度对最大接触应力的响应曲面

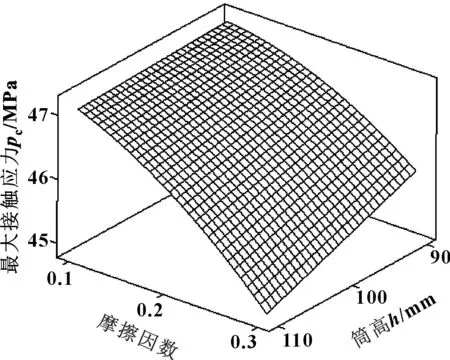
图14 摩擦因数与筒高对最大接触应力的响应曲面

从图11—14中可看出：二因子交互作用的曲面都偏离平面，并且呈较陡的“爬坡”趋势，表明所研究的4个因子交互效应对于响应变量最大接触应力的影响确实是显著的。

根据二因子交互作用的取值范围，在响应优化中对响应变量最大接触应力进行优化分析，结果如图15所示。

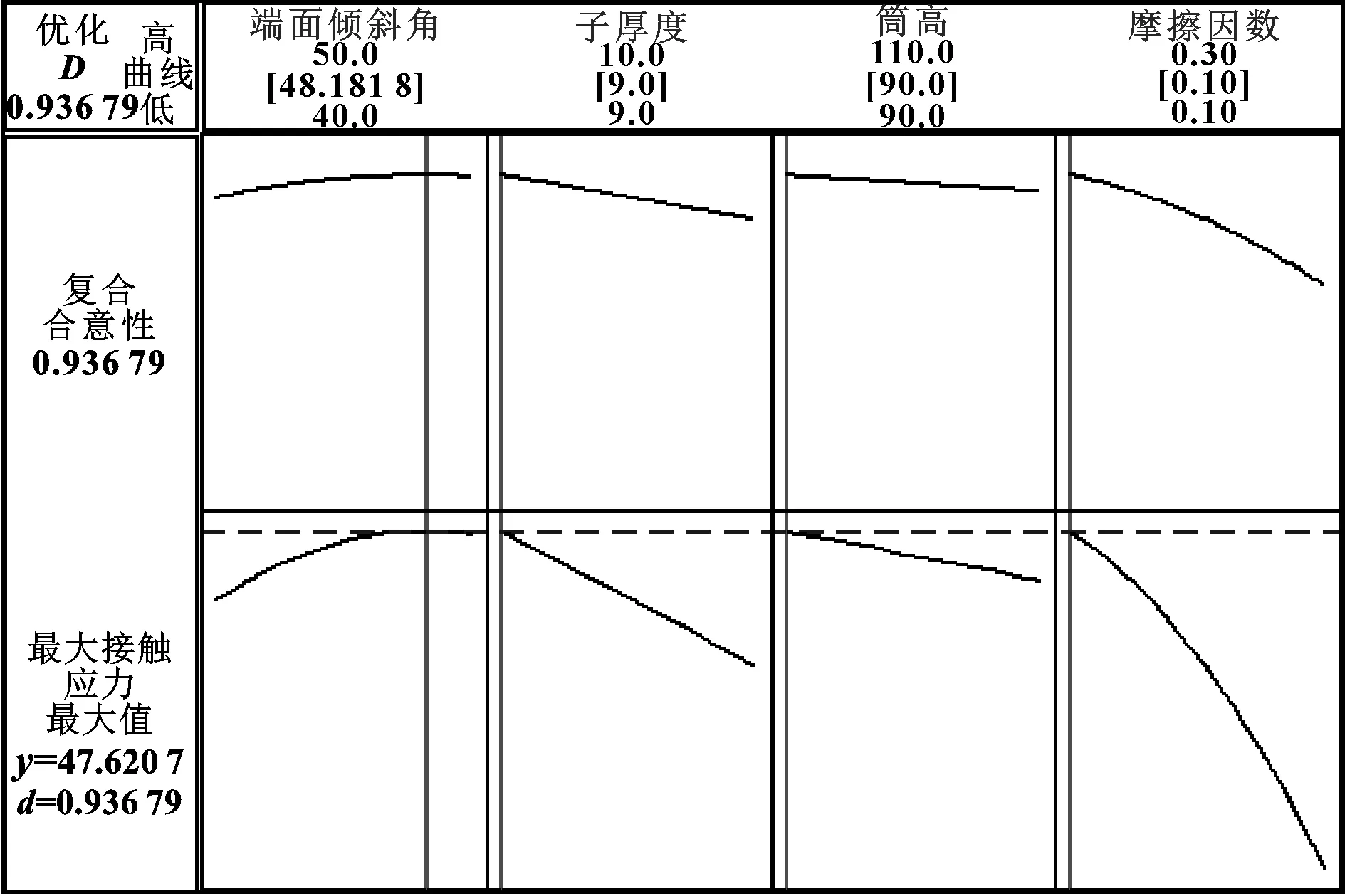
图15 响应变量优化图

优化分析渴求响应效果取得最大值，由d=0.936 79知，响应值十分接近设定目标，因此认为已达到目标值。得到新的因子水平为：

端面倾斜角α=48.2°,子厚度t=9 mm,筒高h=90 mm,摩擦因数μ=0.1;指标最大接触应力pc=47.620 7 MPa。

3.3 响应设计试验验证

将获得的端面倾斜角、子厚度、筒高、摩擦因数的最佳参数值代入有限元中进行验证，得到最大接触应力值为47.351 4 MPa，位于平均值的95%置信区间内，如表4所示，证明响应设计试验结果是有效的，说明模型正确，预测结果也可信。

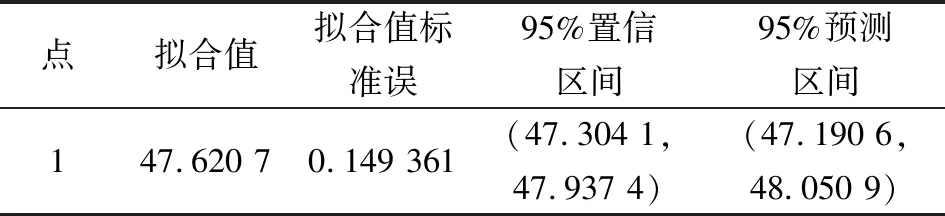
表4 新因子水平的响应预测结果

对比响应优化前后的胶筒与套管接触面接触应力分布(如图16所示)，发现响应优化后新因子水平下的胶筒接触应力整体提高，分布更加均匀，最大接触应力也从45.172 8 MPa提升至47.351 4 MPa，提升了胶筒的密封效果，为安全高效生产提供了保障。

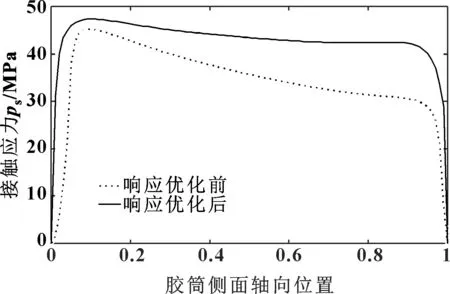
图16 响应优化前后接触应力分布对比

4 结论

(1)在研究的端面倾斜角25°～75°范围内，随端面倾斜角的增大最大接触应力呈W形分布，在端面角等于45°时获得较高最大接触应力值。

(2)在研究的子厚度在7.5～12.5 mm范围内，最大接触应力随子厚度的增加先增大后减小，最后趋于稳定，在胶筒子厚度为9 mm时，封隔器的密封性能较好。

(3)轴向载荷下，胶筒与套管之间的最大接触应力会随胶筒筒高的的增大而减小；但胶筒接触面的最大应力值则随之快速增大。在选择胶筒高度时，要综合考虑胶筒的使用寿命和密封的可靠性。

(4)在研究的0.1～0.8摩擦因数范围内，胶筒与套管之间的最大接触应力值随摩擦因数的增大先缓慢减小后急剧增大，而胶筒侧面的最大应力会快速增大。摩擦因数在0.1～0.3范围内，接触应力分布合理。

(5)通过响应曲面设计分析发现摩擦因数对其密封性能影响最大，筒高影响最小，交互项端面倾斜角和筒高、端面倾斜角和摩擦因数、胶筒子厚度和摩擦因数、筒高和摩擦因数对响应具有显著性影响。当端面倾斜角为48.2°、子厚度为9 mm、筒高为90 mm、摩擦因数为0.1时，密封面的接触应力值最大。响应优化前后的结果表明，胶筒的密封性能得到显著提高。