平板式固体氧化物燃料电池封接气密性的LBM模拟与分析*

2019-04-22

润滑与密封 2019年4期

(华中科技大学能源与动力工程学院湖北武汉430074)

固体氧化物燃料电池(Solid Oxide Fuel Cell，SOFC)是一种全固体结构的高温燃料电池，具有结构简单、能量转换效率高、燃料适应性广等优点，目前正成为洁净发电技术领域极具前景的技术之一[1-3]。然而平板式SOFC在封接技术方面仍面临着巨大挑战。如何确保高温下燃料气和氧化气、内部和外部气体间的有效隔绝，正成为制约其发展的关键技术瓶颈[4]。研究者针对SOFC的密封材料和封接技术展开了广泛研究[5-7]，其中，采用金属、云母和陶瓷等封接材料的压缩密封技术是目前SOFC最常用的密封方法[8-9]。文献[10]指出，压缩密封技术的开发对平板式SOFC的发展至关重要，特别是密封稳定性和密封寿命等问题。

就密封机制而言，压缩密封属于接触硬密封。例如金属材料压缩密封，是将压缩应力作用在具有一定变形能力的金属密封材料上，尽可能减小两个接触表面之间的间隙，以消除泄漏路径。实际上，能够达到零泄漏的理想接触是难以实现的。机加工表面呈现出的复杂粗糙特性使得两个接触硬表面间的连接区域或多或少存在一些孔隙，这些孔隙就是导致泄漏的主要原因。正因为如此，研究者开始通过实验和理论研究的方法对这一连接区域的流体传输特性进行研究，以明确不同工况下封接材料的密封稳定性。一些泄漏模型，如平行平板模型、三角沟槽模型、多孔模型以及分形模型等相继被提出[11]。这些模型的发展在一定程度上反映了人们对接触密封泄漏机制认识的不断深入。

现有泄漏机制模型在实际应用方面还存在不少局限性。例如平行平板模型、三角沟槽模型，采用了简化的泄漏通道，不能反映实际接触过程中泄漏路径的复杂性、随机性；多孔模型[12]和分形模型[13]中，泄漏通道微观参数的实际测量以及与宏观接触模型之间的有效关联还存在不足。文献[14]首次将计算流体动力学(CFD)方法引入接触界面传输特性研究，并基于粗糙表面数值重构技术，通过大量数值计算分析了粗糙表面统计学参数对气密性的影响。文献[11]将分形多孔介质输运理论引入金属垫片泄漏特性研究，提出了金属垫片泄漏率的理论预测模型。这些工作大大拓展了粗糙界面间隙流动的研究方法。

近年来，基于介观尺度的格子玻尔兹曼方法(LBM)被广泛应用于微细空间的流动与传热研究[15]，如多孔介质输运现象[16]、微尺度流动与传热[17-18]、两相流及多相流[19]等，具有算法简单、并行性好且容易处理复杂边界条件等优点，可很好地反映复杂边界对流动与传热的影响。本文作者将LBM引入密封间隙流动的研究，结合粗糙表面数值重构技术以及单粗糙峰微观接触力学分析，建立了SOFC密封结构泄漏率预测模型。该预测模型可实现不同工况、不同工作介质间泄漏率的计算和转换，可为SOFC封接结构精密设计提供理论指导。

1 三维粗糙表面数值模型

文中针对SOFC的金属压缩密封结构进行研究，其封接结构如图1所示，封接位置位于阴阳极两侧气体通道与外界连接处。为与接触力学分析更好地耦合，在泄漏通道构造过程中，两个粗糙表面在粗糙程度相差不大时，可被转化为一个复合粗糙表面与一个理想光滑表面之间的接触；粗糙程度相差很大的情况下，可直接将粗糙程度较小的表面简化为光滑平面。

图1 SOFC密封示意图

研究[20]表明，实际粗糙表面空间各点高度符合高斯分布，文中即采用高斯法来模拟真实的粗糙表面，则表面各点的空间坐标概率密度P(z)可表示为

(1)

实际粗糙表面上相邻各点的高度值并不是完全相互独立的，而是相关的，而且距离越近的点相关性越大。对于粗糙表面上在x、y方向上距离分别为τx、τy的任意两点，相关性计算时的加权值P(τ)：

(2)

式中:σ是粗糙表面的均方根高度，即粗糙度；T为两点间的自相关长度。

应用MATLAB生成符合方程(1)和(2)点阵，再通过快速傅里叶变换和逆变换技术，即可得到数值高斯粗糙表面。

图2示出了粗糙度σ对粗糙表面形貌的影响。可以看出：σ越大，粗糙表面起伏越为剧烈，表面越粗糙；反之，粗糙表面起伏则较为平缓，表面愈趋平滑。总体来说，粗糙度σ对表面形貌有着较大影响，也必然对压缩密封接触界面区域微孔结构产生较大影响。

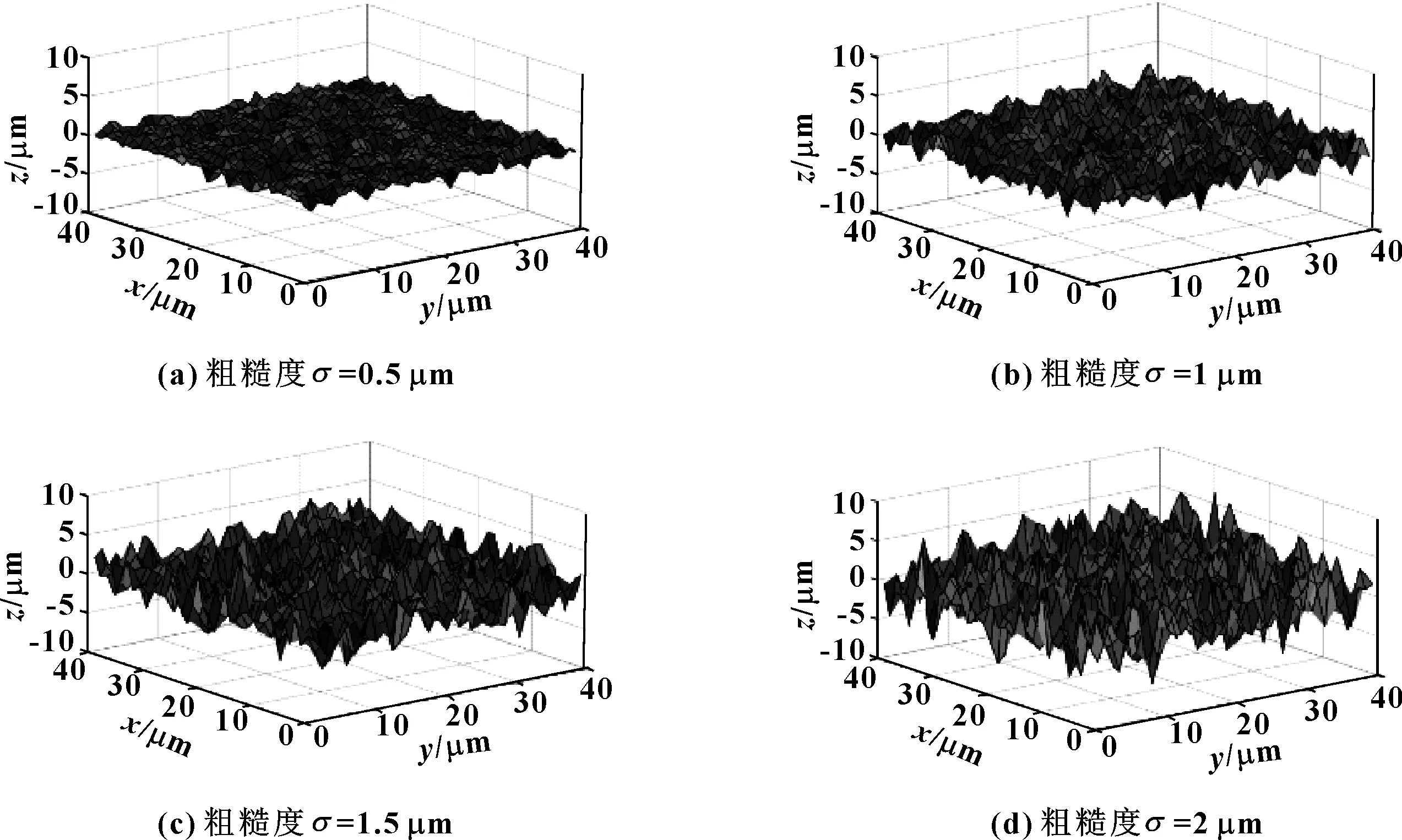
图2 粗糙度σ对粗糙表面形貌的影响

2 间隙流动的格子Boltzmann模型

2.1 D3Q19模型

针对三维流动问题，文中采用了单松弛D3Q19模型[21]，即将间隙流动划分成具有19个速度方向的三维正方体网格。有研究[22]表明，当Knudsen数Kn≤0.047 6时，可忽略气体滑移流效应对泄漏率的影响，文中所研究尺度范围均满足此要求，故采用非滑移的边界条件——反弹格式处理碰撞边界，其中模型中各方向矢量为

(3)

通过单松弛BGK近似的波尔兹曼方程可以离散为

gα(xi+cα·Δt，t+Δt)-gα(xi,t)=

(4)

式中：τ为松弛时间;gα为是沿α方向的单粒子速度分布函数。

对于不考虑热交换的流体，D3Q19模型的平衡分布函数由下式给出：

(5)

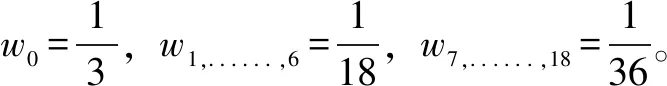
宏观密度ρ和速度u与分布函数相关：

(6)

使用Chapman-Enskog扩展，可以将方程(4)恢复成二阶精度下的Navier-Stokes方程，得出运动黏度为

(7)

2.2 平行平板间隙流动的LBM分析

为验证模型的准确性，将上述D3Q19模型应用于平行平板间隙流动的模拟，并进行了计算分析。该平行通道的高为h，长为l，宽为B，由泊肃叶流动解析式，体积泄漏率QV公式为

(8)

采用LBGK-D3Q19模型，改变间隙高度模拟的体积泄漏率与理论解的比较如图3所示。

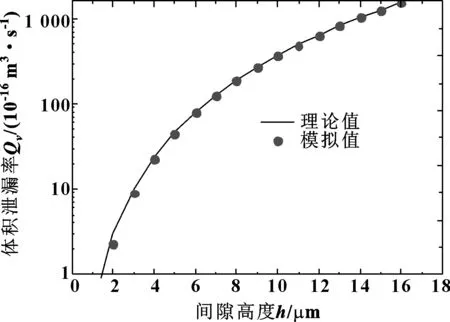
图3 不同间隙高度下平行平板流泄漏率模拟值与理论值比较

可以看出，LBGK-D3Q19模型对三维平行平板间的间隙流动具有较高的准确性，模拟值与理论值相差极小，且随着间隙高度的增加，准确性越来越高。

2.3 粗糙间隙内流动的LBM分析

考虑到所研究区域内粗糙间隙高度远小于泄漏长度和宽度，对于间隙空间和流体介质做出如下假设：

(1)金属表面的粗糙度各向同性、均匀分布，即不考虑加工纹理(即自相关长度T取1 μm)；

(2)忽略体积力的影响，如重力。

满足上述假设的间隙流动可认为是流动特性均匀一致。这样，可以通过对一个包含足够多粗糙峰信息的微小表征区域进行数值分析，进而推算出整个区域的泄漏率。文中选取40 μm×40 μm的计算区域，并进行了尺寸独立性检验。

两个紧密接触的粗糙表面，当粗糙程度相当时，真实接触状态难以模拟，借助摩擦力学[23]中常用的方法，将两个粗糙表面的无摩擦接触用一个光滑平面和一个复合粗糙表面的接触来代替，即把泄漏通道上下两侧的两个粗糙表面简化成一个光滑表面和一个等效粗糙表面，计算模型及边界条件如图4所示。图中，上表面为等效粗糙表面，下表面为理想光滑表面，均设置为无滑移反弹边界条件；左右设为对称边界条件；进出口为zou-he压力边界条件；间隙高度定义为上基准面与下表面之间的距离。

图4 模型计算域及边界条件

为有效分析粗糙度σ和间隙高度h对泄漏率的影响规律，文中共构建了55个不同参数的计算区域，其中粗糙度σ取值有5个，分别为1.4、1.56、1.7、1.85、2 μm，间隙高度取值共11个，等距离分布在5～15 μm之间。模拟过程中，所有表面自相关长度T均为1 μm。

图5为不同高度截面速度分布图。可以看出：粗糙峰的存在对流体流动有较大影响，流动比较大的区域集中在粗糙峰占比较小的截面，如图中z=4 μm处。随着粗糙峰占比的增大，如z=5 μm和z=6 μm处，流体的流动路径蜿蜒曲折，远远偏离了泊肃叶流动。当z=7 μm时，由于孔隙空间的急剧减少，流动仅在局部地方发生。图5的结果说明，考虑三维模型以及采用基于介观尺度的LBM来研究粗糙壁面间隙流动是十分必要的。

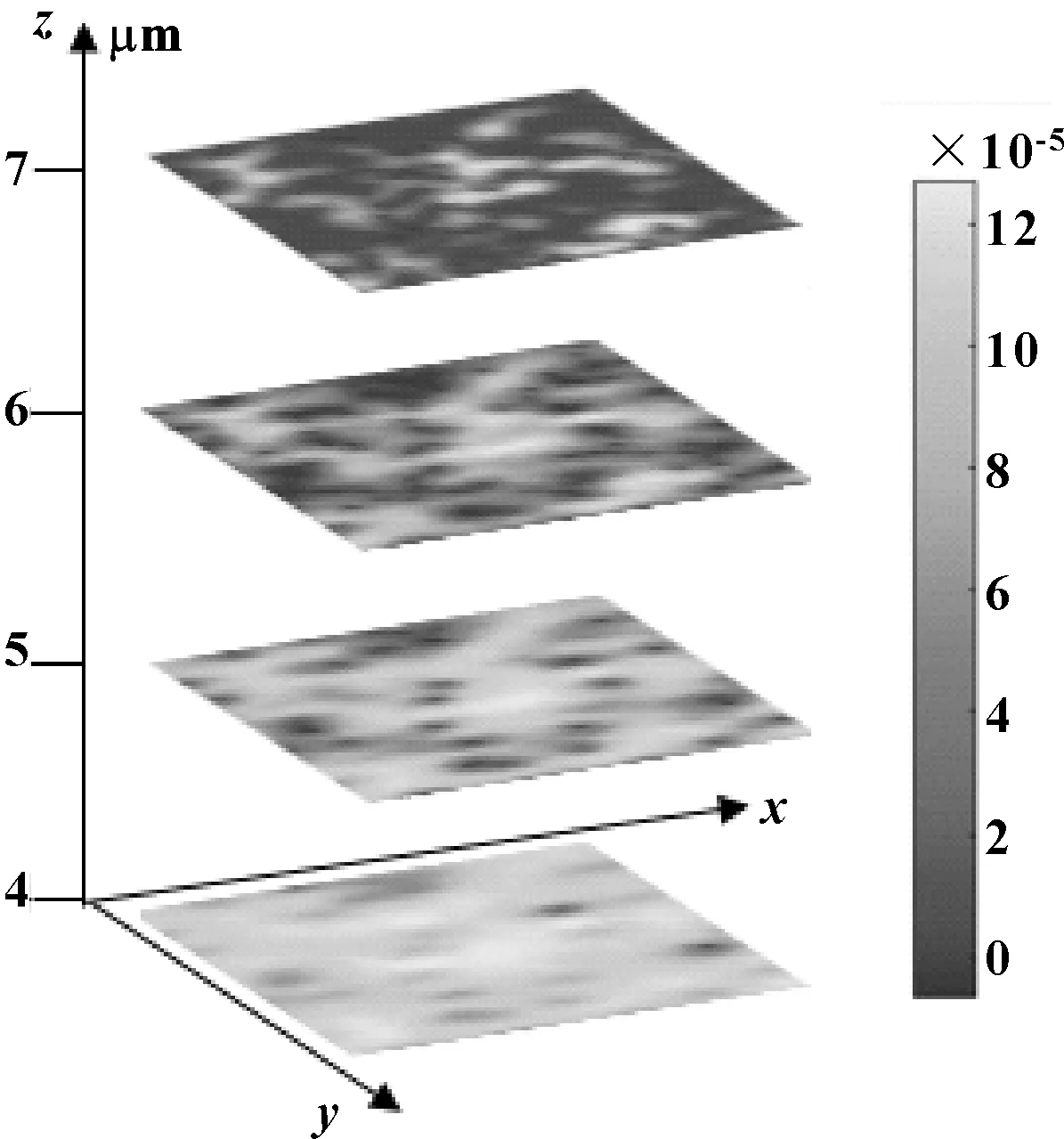
图5 沿间隙高度方向截面量纲一速度场分布(h=8 μm,

图6给出了给定内外压差的条件下，间隙高度和粗糙度对体积泄漏量的影响。可以看出：同样间隙高度条件下，粗糙度越大，体积泄漏率越小；不同粗糙度下泄漏率随间隙高度变化的规律十分相似，在间隙高度较小时，与泊肃叶流动偏差较大；当间隙高度较大时，与泊肃叶流动偏差较小。可见，粗糙峰形貌是造成粗糙壁面间隙流动与平行平板流动差异的主要原因。因此，可以引入流量因子Φ来表征二者流量的差异，即:

(9)

式中：Q和Qp分别为间隙高度相同的粗糙间隙与光滑间隙的体积泄漏率。

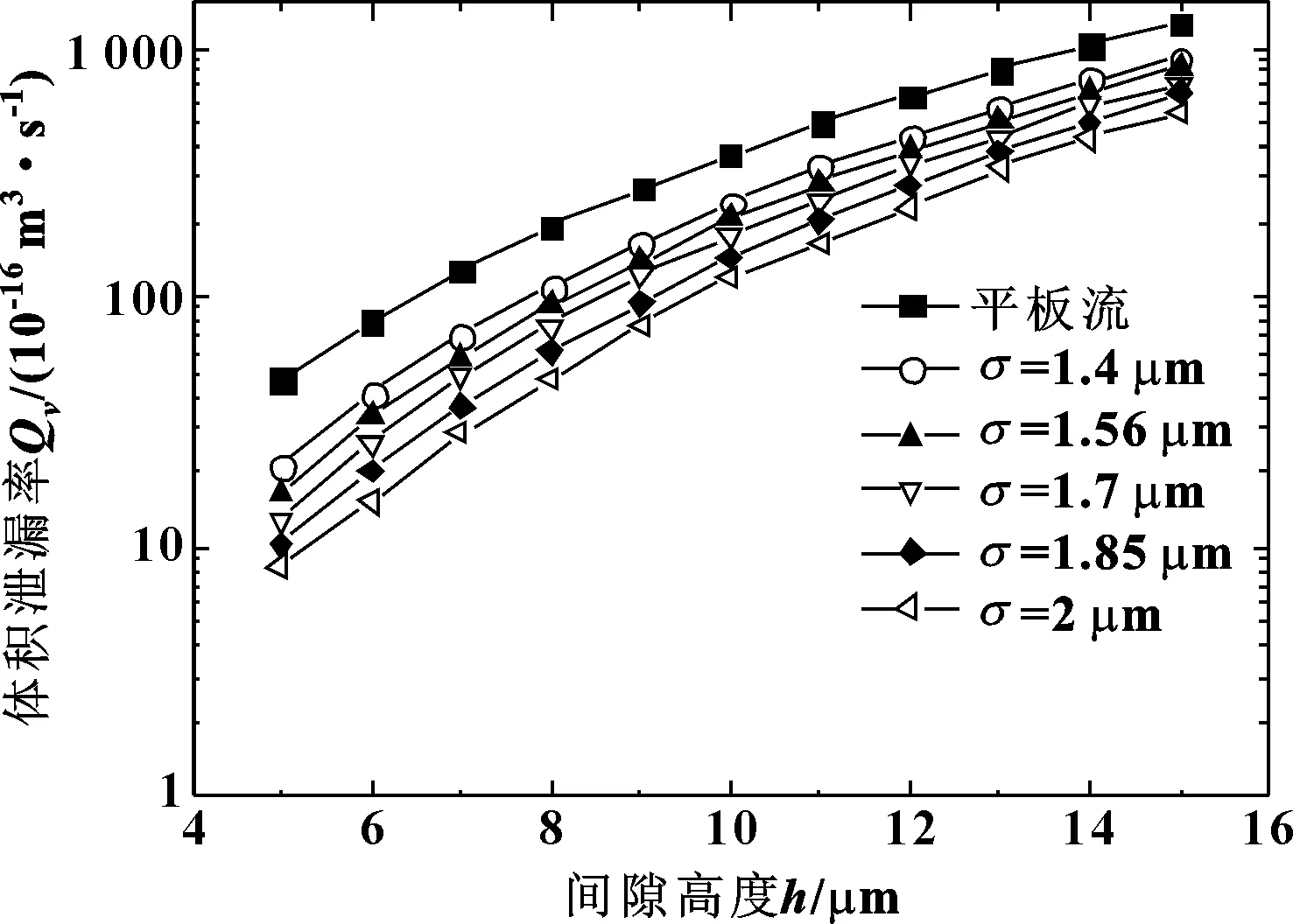
图6 间隙高度和粗糙度对体积泄漏量的影响

流量因子Φ反映了粗糙度对流体流动的影响，与粗糙度σ、间隙高度h有关，根据LBM模拟结果整理可得如下拟合公式：

(10)

3 接触状态下的泄漏率预测

3.1 密封间隙高度随应力变化

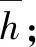
(11)

式中:SG为接触区的平均压力，MPa;h0为初始密封间隙高度，取为5倍于粗糙度。

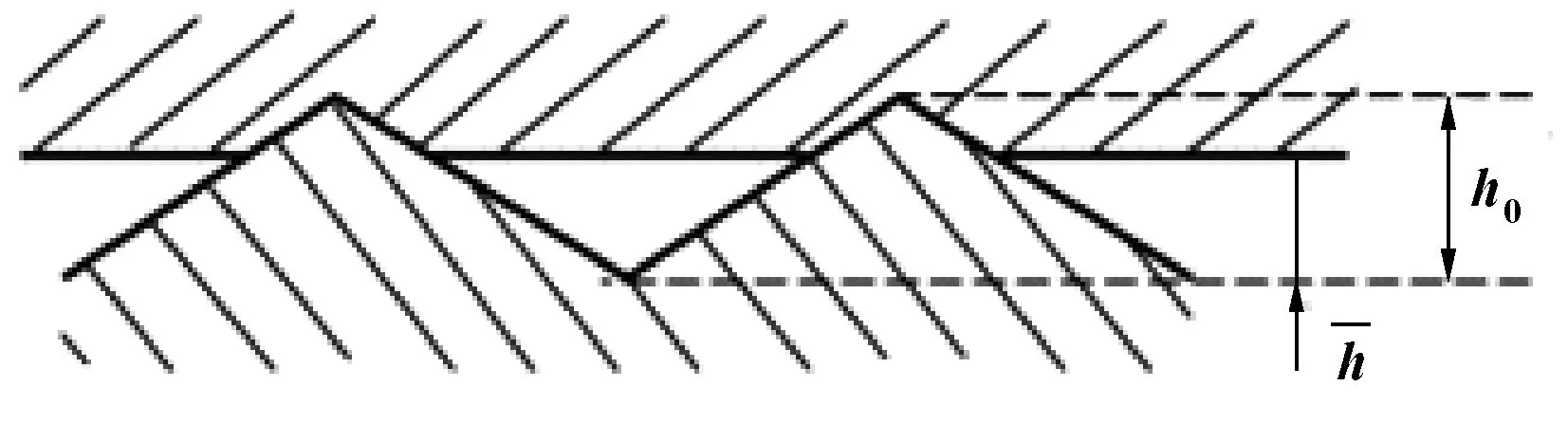
图7 接触状态下粗糙界面接触示意图

3.2 预测模型及验证

为了验证所提出的泄漏率预测模型的正确性，将不同工作条件下SOFC密封泄漏率的预测值与文献[25]报道的实验数据进行比较。为模拟燃料电池的工作状态，实验在25、250、500 ℃ 3个温度下进行，内外压力差为2.0 kPa，工作流体为氦气，其流动方向设计为仅沿径向。金属材质分别为因科镍合金及奥氏体不锈钢。测试的2个不锈钢试样分别用100和600目砂粒工具加工，对应于粗糙度分别为1.85和1.56 μm。因科镍合金加工精细，粗糙度较小，视为光滑表面。实验模型简化示意图如图8所示，实验参数见表1。

图8 实验示意图

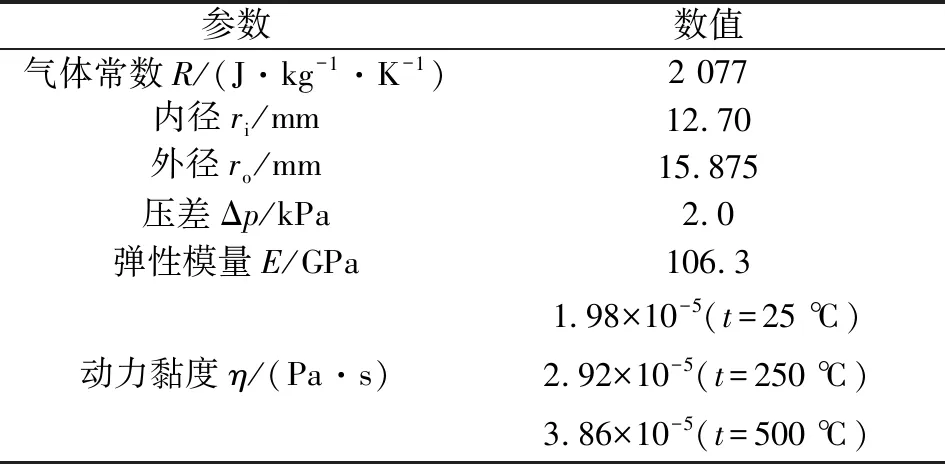
参数数值气体常数R/(J·kg-1·K-1)2 077内径ri/mm12.70外径ro/mm15.875压差Δp/kPa2.0弹性模量E/GPa106.3动力黏度η/(Pa·s)1.98×10-5(t=25 ℃)2.92×10-5(t=250 ℃)3.86×10-5(t=500 ℃)

表2和图9分别给出了模型预测值与实验值的数值和趋势比较。由表2可以看出：模拟值与实验数据非常吻合，特别是针对载荷较大且温度较高的工况，二者的误差相当小。图9给出了σ=1.85 μm时泄漏率随温度变化的模拟结果及相应的实验值，可以看出：模型预测的泄漏率随温度变化趋势与实验测量结果完全一致，温度的升高会导致泄漏率的降低，降低的趋势先快后缓。上述结果反映了预测模型的准确性。

表2 泄漏率模拟值与实验值比较

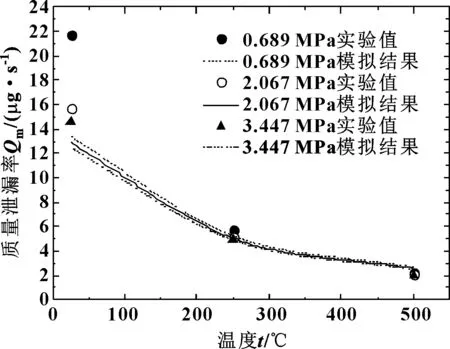
图9 不同载荷下泄漏率随温度变化实验值与模拟值

Fig 9 Experimental results and simulation values of leakage rate with temperature under different loads

3.3 泄漏率的影响因素

利用文中提出的预测模型，针对各种实际工况，在给定粗糙度、工作介质以及接触平均载荷情况下，通过式(8)、式(10)以及式(11)可以计算得到相应泄漏率，可以反映表面粗糙形貌、工作介质、载荷、温度对泄漏率的影响。

图10给出了由计算得到的泄漏率随各种影响因素的变化趋势。总体而言，随温度的升高，质量泄漏率会呈现下降的趋势，主要原因在于泄漏介质密度与温度成反比关系。需要指出的是，虽然从正常工作状态来看，温度升高对泄漏率减小是有利的，然而实际工况下，温度过高会导致密封结构失效。这是因为，温度升高会影响密封结构的力学特性，以及不同材料热膨胀系数差异会引起界面应力减小或增大。文中提出的模型结合了这些材料力学特性，因而可以很好地给出预测，这方面将在今后的研究中进行详细讨论。

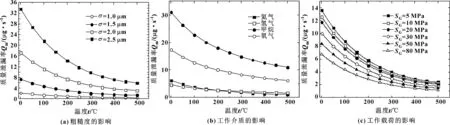
图10 不同温度下表面粗糙度、工作介质、载荷对泄漏率的影响

图10(a)表明，相同温度相同载荷下粗糙度越小，泄漏率越小，且随着粗糙度的减小，温度对泄漏率的影响逐渐越弱。此处与前文3.3节并不矛盾。在3.3节中，并未涉及接触分析，是在同一有效间隙高度h下进行的模拟，此时粗糙度σ对泄漏率的影响体现在偏离平板流的程度，h相同，σ越小，粗糙面越接近光滑平板，泄漏率就越大。而图10(a)中是将粗糙表面界面流动分析和微观接触分析耦合后得到的结果，由式(8)可知泄漏率与h的3次方成正比，而由微观接触力学分析得h与σ成正比，所以σ越小，h就越小，故而泄漏率越小。图10(b)表明，介质的物性变化(主要是黏度和密度)对泄漏率亦会产生较大影响，其中甲烷的质量泄漏率最大，氢气与氦气泄漏率较小，主要是因为相同情况下其运动黏度较大。图10(c)则表明，在所考虑应力范围内，压缩应力对泄漏率的影响并不是很大。温度较低时，应力从5 MPa变化到80 MPa，泄漏率降低50%；而当温度较高时，泄漏率整体偏低，压缩应力的影响并不明显。平均应力的作用不明显，主要与金属材料在所考虑应力范围内产生的变形量极小有关。