T形槽气膜密封槽底粗糙度有序造型的扰流效应*

2019-04-22晨屹

润滑与密封 2019年4期

晨屹

(1.淮海工学院机械与海洋工程学院江苏连云港 222005；2.江苏省海洋资源开发研究院江苏连云港 222005；3.南京天一航空科技有限公司江苏南京 210012)

干气密封的低磨损、长寿命特点使其应用范围日趋广泛[1]，但受加工水平的制约，干气密封槽底面精度一般只能达到0.8 μm，与正常运转时密封副间膜厚仅差1个数量级，在启动或停车阶段甚至为同一数量级，因此干气密封的研究必须考虑表面粗糙度的影响[2-3]。1978年，PATIR和CHENG[4]提出“平均流动模型”的概念，通过引入流量因子表征粗糙度建立了PATIR-CHENG模型，为研究表面粗糙度的润滑效应提供了重要手段。此后ELROD[5]、TRIPP[6]、TONDER[7]、HU和ZHENG[8]、MAKINO等[9]对PATIR-CHENG模型进行了持续研究和完善。

国内相关研究团队也做了较多开创性工作。彭旭东教授团队的研究结果表明：端面不同区域的表面粗糙度对密封性能影响规律差异较大，且转速的影响不可忽视[10]；一定工况条件下，粗糙表面密封开启力、气膜刚度和摩擦扭矩均大于同条件下的光滑表面[11]。近期，该团队还研究阐述了滑移现象的产生与气体分子平均自由程、粗糙度的关系[12]。宋鹏云教授团队[13-15]近年的研究表明：当膜厚与粗糙度均方根的比值大于3～4时，可基本忽略表面粗糙度对密封性能的影响；较大粗糙度可以提升开启力和气膜刚度，但泄漏率也会显著加大。

2016年，SLAWOMIR和ANDRIY[16]研究了干气密封微槽道、微孔隙及表面纹理的改变对密封介质层动态属性的影响，指出合理的设计和表面形貌有助于提高干气密封稳定性。

综上，干气密封表面微造型的合理重构对密封性能具有直接影响。但通过该领域国内外文献及专利情况检索，目前国内外研究人员尚未涉及干气密封槽底界面有序设计下的扰流效应研究，这是干气密封稳定性研究中亟需解决的问题。

1 激光加工模型的建立

现有加工水平下干气密封动环非开槽区及静环表面的粗糙度一般为0.1 μm[10]，槽底区域的粗糙度一般为Ra0.8 μm[17]。假设模型非开槽区及静环区为光滑表面，槽底粗糙度表面为各向同性，示意图如图1所示。

图1 槽底粗糙面三维轮廓图

相关文献[18-19]研究表明，表面粗糙度纹理方向对表面摩擦学性能和密封性能有重要影响。采用激光加工技术根据扫描路径可实现一定的纹理结构，假设扫描路径依据流体泵入方向呈一定有序，则雕刻后的槽型槽底粗糙度将整体呈有序性造型，如图2所示。

图2 有序微造型示意图

激光雕刻过程中，影响槽底加工精度(深度和平面度)的参量主要有焦距、步长、功率及频率。为保证精度，在焦距调整完成后，一般初始雕刻采用高功率、大步长、低频率进行高效雕刻，而在开槽结束阶段，为保证较好的底面粗糙度，采用降低功率、减小步长、提高频率进行精细雕刻。这种加工方法虽然可以在一定程度上确保精度，但效率低、成本高，具体加工方法如图3所示。而对于具有微造型的干气密封，由于槽底槽型本身微造型的存在，可免去开槽最后阶段进行的精细雕刻过程，采用固定雕刻参数即可，如图4所示。

图3 无微造型干气密封开槽基本步骤

图4 具微造型开槽基本步骤

本文作者以具有微造型的T形槽干气密封(简记MT-DGS)为例，通过对干气密封槽底粗糙度进行有序重构及系统研究，探索粗糙度有序造型对密封性能的影响机制。

2 模型设计

2.1 流态计算说明

目前，对干气密封微尺度流场流态属于层流或湍流仍存在争论。部分学者的研究表明[20-21]，当入口压力pin=0.4～0.5 MPa、转速n=10 000 r/min左右时，实际流态选择为层流与实际更为符合；而部分学者[22-23]在压力较高(pin=4.585 2 MPa)、转速n=10 000 r/min左右时，则选用湍流形式进行求解计算。但整体而言，流态选择的不同对计算结果具体的数值影响较大，但不会改变相关参数影响的规律性。鉴于文中压力和速度取值较大，所以将干气密封副间流体流态视为湍流流动。

2.2 基本假设

(1)密封副间气体为连续介质流动；

(2)密封副间流体属于牛顿湍流流体[20]；

(3)流场内润滑层温度、黏度相等；

(4)气体分子与密封表面牢固吸附，无相对滑移；

(5)忽略密封环变形对气体流动的影响；

(6)忽略气体的惯性力和体积力；

(7)密封副在运行过程中始终保持平行，除T形槽底面之外，其他表面均为光滑表面。

2.3 几何模型

图5所示为开槽几何模型和采样计算区域。若槽数为Ng，则可选择整个密封端面的1/Ng份(图中区域ABCD)作为计算区域。

图5 开槽端面几何结构示意图

如图6所示，依据流体泵入方向及流体力学原理，拟定槽型的流线型微造型结构。有序造型位于槽底且沿槽形均匀分布，忽略密封环曲率的影响，将粗糙度有序造型简化为矩形微造型。考虑粗糙度的复杂性，通过改变微造型的宽度、间距和深度近似表征不同粗糙度(图中粗糙度为放大表示)。

图6 有序造型示意图

2.4 计算模型

根据假设条件和几何模型，选用YAKHOT和ORZAG提出的RNGk-ɛ湍流模型，表达式[21]如下

(1)

(2)

2.5 边界条件

密封槽入口ro处为介质高压侧，用pout表示，为外界压力(变量)；出口ri处为环境低压侧，用pin表示，为恒定大气压。控制方程在计算区域内满足周期性边界条件[25]：

对称边界Γ1和Γ2处压力相等：p|Γ1=p|Γ2，即p(θ+2π/Ng)=p(θ)。根据质量流量守恒，流过对称边界Γ1和Γ2处的质量流量也分别相等：q|Γ1=q|Γ2。

3 仿真计算

3.1 建模及网格划分

鉴于微造型模型的复杂性，其径向与厚度方向尺寸差距达4个数量级。在建模时将厚度方向放大1 000倍后导入Gambit中进行网格划分，如图7所示；采用逐层拉伸的形式将面网格拉伸成体网格，依次是非槽区、槽区和微造型部分，可精确保证网格的一致性且避免了Interface的设置；3个部分的网格层数通过Interval count分别定义为6、6、4；最后导入Fluent中，通过scale设置可实现模型厚度还原。

图7 网格划分

3.2 边界设置

如图8所示，周期边界为2组，出口边界1个，进口边界为2(非槽区气膜及槽区进口)+n(微造型数量)个，气膜底面为Static wall，其余面为Rotational wall。

图8 边界条件设置

3.3 求解设置

仿真计算选择三维双精度求解器，密封介质为空气，压力速度耦合采用SIMPLEC算法。扩散项的离散格式采用中心差分格式，对流项的离散格式采用二阶迎风格式，以提高计算结果的精度。模型采用的迭代精度设为10-5。

4 参数选择

4.1 验证性实验

为验证方法的正确性，选择文献[26]中的参数进行计算。选择端面开启力Fo和泄漏率Q为参量。

表1 验证性参数

4.2 分析性实验

为研究槽底有序造型设计对密封扰流性能的影响，槽型几何参数及微造型参数列于表2和表3。

表2 分析性参数

表3 微造型参数

5 计算结果与分析

5.1 验证性分析

图9所示为依据表1参数得出的膜厚为2.03 μm时的压力分布图。可以看出：T形槽一侧形成高压区，另一侧为低压区。槽型的对称性使得当转速方向变化时，高压侧和低压侧具有转换性，密封实际动压效应不变，这是非对称槽型不具备的可双向旋转特性。

图9 T-DGS压力分布云图 (δ=2.03 μm)

图10、11分别示出了采用文中计算方法得到的开启力和泄漏率与文献值[24]的比较。可以看出：在较大膜厚时文中计算结果与文献值很接近，且变化趋势和规律性也与文献符合较好，验证了该方法及参数设置的正确性。

图10 开启力对比

图11 泄漏率对比

5.2 具微造型性能分析

图12示出了MT-DGS与T-DGS性能对比。可知，具微造型干气密封MT-DGS与T-DGS规律变化趋势一致，在小膜厚时MT-DGS的开启力略高。鉴于膜厚的变化区间较小，无法充分反映性能参数的变化规律和具体区别，选择小膜厚时(δ=1 μm)及其他微尺度工况进行进一步性能分析。

图12 MT-DGS与T-DGS性能对比

5.3 微尺度下的性能分析

图13示出了微尺度下T形槽干气密封开启力分析结果。

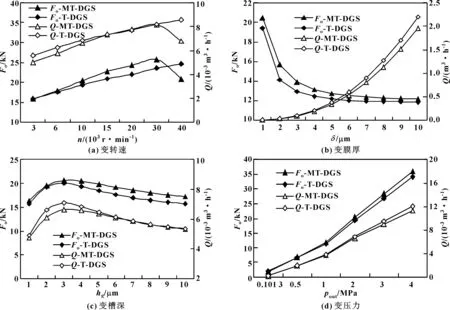
图13 微尺度下T形槽干气密封开启力分析

从图13中可以看出，微尺度下MT-DGS较无微造型T-DGS具有良好的增压减漏效果。几何参数和工况参数的变化对MT-DGS和T-DGS都有一定的影响，具体为：开启力随转速和压力的升高而增大，随膜厚的增大而减小；泄漏率随转速、压力和膜厚的升高都呈增大趋势，MT-DGS较T-DGS的增压减漏效果随转速、压力、槽深、膜厚的增大愈加明显；存在一定的槽深(图示为5～7 μm)使得具MT-DGS的泄漏率不大且兼具良好的开启性能。值得关注的是，如图13(a)所示，微造型结构在高转速下具有一定的抑制泄漏率作用，可能的原因是槽底微造型的存在形成的扰流作用具有抑漏效果，关于这一点下文将继续探讨和研究。

6 微造型扰流效应分析

文中所述扰流指工况条件变化时槽底产生的流动流体的相互干扰，即文献[27]中研究结果表述的动压叠加效应。对于干气密封，理想的流体流动形式(层流或湍流)都是有助于形成密封副间的开启力，出现动压效应叠加时(扰流)可能产生流体回流、空化等降低密封开启性能的因素，所以应对其进行深入研究。

图14所示为MT-DGS与T-DGS在不同槽深和膜厚下随转速变化时的开启力对比结果。可知：槽深和膜厚的变化对二者的开启力都有较大影响；在槽深hg=1 μm时MT-DGS与T-DGS的开启力受扰流效应影响较大，都随转速升高开启力逐渐减小；在槽深hg=3 μm时二者的开启力随转速升高呈现先增大后减小趋势；在槽深hg≥4 μm时T-DGS的开启力随转速升高而增大，MT-DGS的开启力则呈现先增大后减小趋势。

图14 不同槽深时T形槽干气密封开启力变化(pout=2 MPa)

微造型结构在槽深hg≥3 μm时扰流效应在一定转速下是有益于密封开启性能的，随着转速的增大，扰流效应逐渐起到主导作用，降低了微造型结构的开启力，开启力下降拐点随槽深增大逐渐由20 000 r/min升高至30 000 r/min；槽深hg=1 μm时，微造型结构由于受扰流效应影响，开启性能较差；膜厚越小，微造型的开启力提升效果越明显，一定膜厚(δ≤2 μm)及槽深范围内(hg≥3 μm)，MT-DGS的开启性能优于T-DGS；分析图14(a)、(b)所示的开启力的变化趋势可以发现，MT-DGS随转速升高开启力的变化幅度更大，说明微造型结构对速度变化更加敏感。

图15所示为不同槽深和膜厚时MT-DGS和T-DGS泄漏率的对比结果。可知：MT-DGS和T-DGS的泄漏率变化趋势一致，随膜厚的增大泄漏率呈增大趋势。较大膜厚时，泄漏率随转速的增大而减小的可能原因是扰流效应下气体的回流效果造成的。在膜厚逐渐增大时，微造型结构干气密封的减漏效果愈加明显，同样说明具有微造型的T形槽受扰流影响的程度大于无微造型T形槽结构。