基于QPSO-SVR和声发射信号的机械密封寿命预测*
2019-04-22
(西南交通大学机械工程学院 四川成都 610031)
机械密封作为大型旋转设备中必不可少的装置,因其体积小、泄漏量小、可靠性高等优点,广泛地应用于石油化工等过程工业大型旋转设备[1]。据调查显示,在旋转设备中其使用率高达90%。机械密封的性能状态直接影响生产过程中的安全和效率,因此对机械密封进行状态监测和寿命预测尤为迫切。
长期以来,众多学者致力于机械产品性能监测方法的研究,而寿命预测是机械密封健康监测中的重要组成部分,它对避免重大事故的发生和预知性维修具有重大意义。常用的寿命预测方法有2种:一是基于产品失效机制进行寿命预测;二是在数据驱动下通过机器学习或人工智能算法,对观测数据进行深度分析、挖掘及融合,得到产品的退化曲线,从而得到剩余使用寿命。由于机械密封涂层摩擦副的退化过程很难建立相应的物理失效模型,考虑到机械密封失效机制是基于累积损伤的退化过程,通过得到完整的寿命周期数据,确定失效阈值,就可以使用支持向量回归预测模型建立退化模型[2-3]。
声发射检测方法是一种无损检测方法,作为非接触式传感方式,被大量应用于工业现场实时监测作业。声发射实质上是应力波,是由于材料局部能量快速释放而产生的瞬态弹性波[4]。CHOUDHURY和TANDON[5]利用声发射参数对轴承故障进行了诊断和预测。单一的声发射参数虽然分析速度较快,但是分析准确度低,易受环境影响[6-7]。
支持向量回归(SVR)是近年发展起来的统计学习理论,具有泛化能力强、训练时间短、全局优化和抗干扰能力强等优点,在工程领域有着广阔的应用。传统的参数选择方法具有一定的盲目性,小幅的参数变化将会导致结果的巨大偏差[8-10]。面对大量数据样本时,普通SVR算法的复杂度会大量增加,导致预测准确度和模型泛化能力急剧下降[11]。
针对上述问题,本文作者以金刚石涂层机械密封为研究对象,通过声发射技术建立设备运转时的声发射信号与密封性能之间的关系,提出了基于声发射特征融合的退化指标和QPSO-SVR寿命预测模型的机械密封剩余寿命预测方法。实验证明,该模型能对机械密封寿命做出较好的预测,从而为机械密封寿命预测的工业应用提供了良好的技术支撑。
1 金刚石涂层机械密封寿命实验
1.1 密封失效形式分析及检测方式的选择
机械密封失效成因包括化学损坏、热损坏和机械损坏,分别体现为腐蚀、过热和磨损[12]。文中实验对象为金刚石涂层机械密封,它的退化过程实质上是涂层脱落和磨损,进而导致密封性能下降,最终导致密封泄漏量增大。声发射技术是一种无损测量手段,可以在不破坏密封物理结构的情况下连续实时地监控密封运行状态,并且涂层的磨损和脱落过程伴随着大量的应力波释放,而声发射现象的实质正是应力波,所以采用声发射技术建立设备运转时的声发射信号与密封性能之间的关系。
1.2 实验装置
实验对象为金刚石涂层机械密封摩擦副,采用声发射传感器监测其声发射信号。机械密封的金刚石涂层厚度为2~4 μm,电机转速稳定在1 790 r/min。实验时对机械密封施加100 N的轴向压力,声发射传感器安装在最靠近机械密封的表面,采样频率为2 MHz。
图1所示为实验中使用的金刚石涂层机械密封环。

图1 金刚石涂层机械密封环
1.3 实验结果
图2、图3是密封匀速旋转时所测得的声发射信号,其中包含了大量的噪声,淹没了有效信息。因此为了提高信噪比,突出寿命信息,将对信号采用小波降噪和特征提取。

图2 声发射信号时域波形
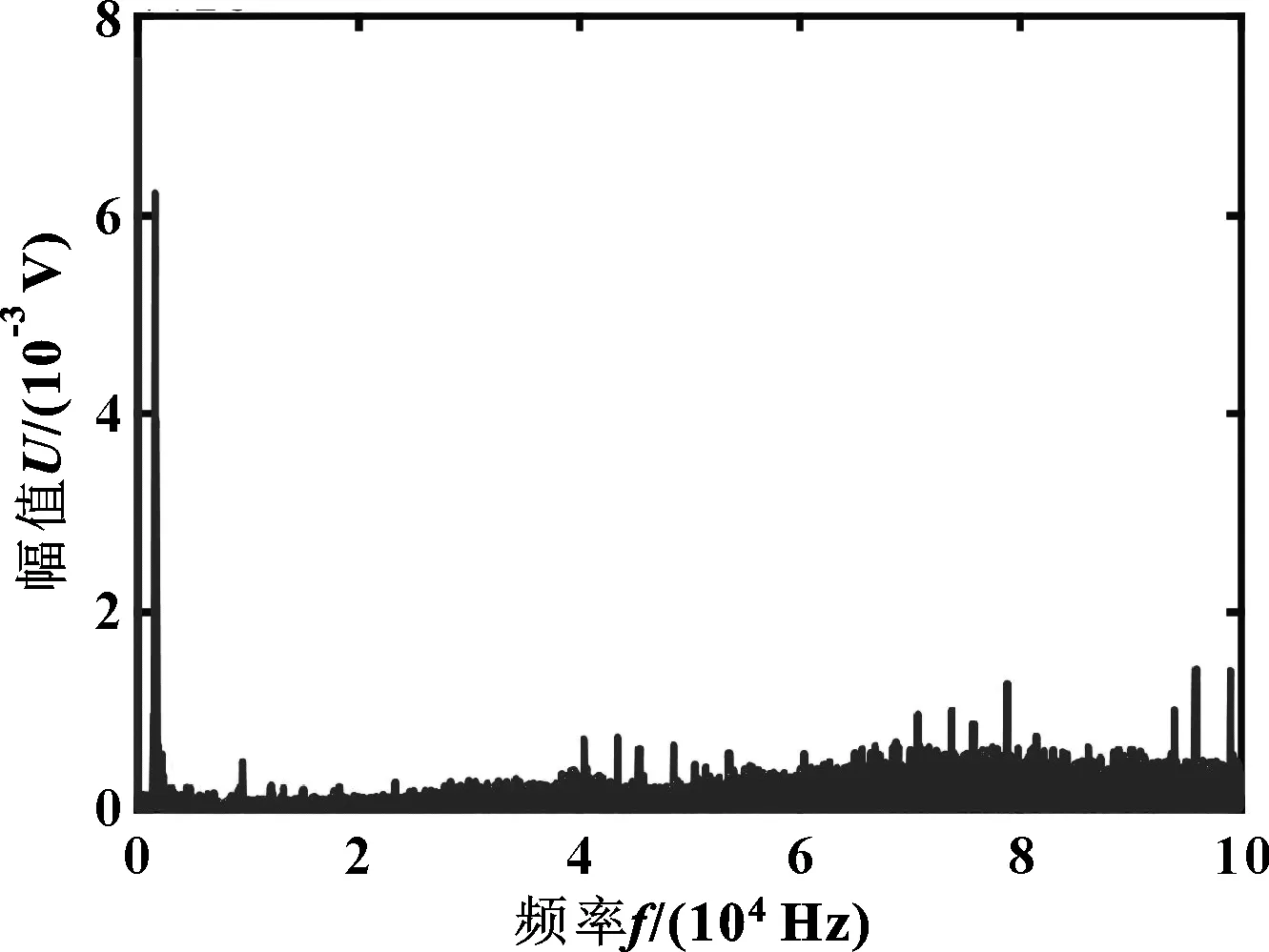
图3 声发射信号频域波形
2 研究方法
由于声发射信号易受环境影响,信噪比较低,难以直接得出有效信息。采用传统声发射参数分析法结合KPCA,将特征进行优化,并且利用马氏距离得出寿命信息,这样不仅降低了特征维数,还削弱了特征之间的非线性相关程度。针对传统SVR预测准确度低、预测效率低且泛化能力差的问题,提出QPSO优化SVR的预测模型,自适应进行参数寻优,对寿命信息进行有效利用,较之普通的SVR有更高的预测准确度。
2.1 特征选择
声发射参数分析法是利用声发射信号的特征参数对声发射源进行定性识别、定量评价[13],主要是在时间域和频率域内对信号进行放大、滤波、统计特征提取等。由于涂层密封的失效形式主要表现为涂层脱落和表面磨损,结合声发射信号的参数分析法,采用的评价指标及评价意义如表1所示。

表1 声发射特征选取
2.2 退化指标
马氏距离是衡量服从同一分布且有着协方差矩阵的随机变量之间的差异程度。假设共有m个样本向量(X1,X2,......,Xm),其中Σ为总体的协方差矩阵,则向量Xi与Xj之间的马氏距离定义为

(1)
2.3 量子行为粒子群算法(QPSO)
量子行为粒子群算法是一种应用度广、适应性高的优化算法。其主要思想是通过在解空间初始化一个粒子群,以适应度函数评价粒子的优劣,用最优个体更新迭代,最后得到一个全局最优解[14]。
假设一个包含m个粒子的粒子群在D维解空间中飞行,在t时刻,第i个粒子位置表示为Xi(t)=Xi,1(t),Xi,2(t),......,Xi,D(t),其中i=1,2,......,m。第i个粒子在D维解空间中的历史最优位置表示为Pi(t)=[Pi,1(t),Pi,2(t),......,Pi,D(t)],群体的全局最优位置表示为G(t)=[G1(t),G2(t),......,GD(t)],且G(t)=Pg(t),其中g是全局最优位置粒子的下标,g∈1,2,......,m。个体最优位置的平均表达式为
(2)
对于最小化问题,目标函数值越小,对应的适应值越好,故第i个粒子的个体最优位置Pi(t)表达式为
(3)
群体的全局最优位置G(t)为
(4)
粒子位置进化方程为
Pi,jt+1=φj(t)·Pi,j(t)+1-φj(t)·Gj(t)φj(t)∈U0,1
(5)
Xi,jt+1=Pi,j(t)±α·Mbest(t)-Xi,j(t)·ln1/ui,j(t)ui,j(t)∈U0,1
(6)
其中,φj(t)、ui,j(t)为(0,1)区间均匀分布的随机数,若ui,j(t)大于0.5,α前取负号,否则取正号。
2.4 支持向量回归

(7)
再引入惩罚参数c和拉格朗日乘子,对w、b求偏导,则可以将w和b的求解问题转换为一个凸二次规划问题:
(8)

选择适当的核函数Kxi,x代替上式中的内积运算φ(xi),φ(xj),即可构造出回归函数:
(9)
支持向量回归最大的特点是以统计学习理论为基础,实现小样本条件下的学习方法和统计规律,而且结构简单,在机械密封寿命预测方面有一定的优越性。
2.5 量子行为粒子群算法优化支持向量回归(QPSO-SVR)
传统的SVR需要输入惩罚参数c和核函数参数g,这2个参数与支持向量回归的预测准确度息息相关。针对这种情况选用广义交叉验证(GCV)风险函数作为QPSO优化支持向量回归的适应函数,通过目标函数最小化来选取渐进最优参数c和g。其主要步骤为
(1)对最佳惩罚参数和最佳和函数参数进行编码;
(2)确定适应函数为CGV风险函数;
(3)初始化粒子群,确定迭代次数;
(4)输入样本数据,计算粒子的适应度;
(5)判断粒子适应度是否达到要求,如果达到要求就进行解码,如果未达到要求重新计算粒子群的平均最优位置,继续进行迭代,直至满足条件;
(6)将解码后的最佳惩罚参数和核函数参数用来建立支持向量回归模型;
(7)利用该模型进行寿命预测。
2.6 机械密封寿命预测方法
针对传统声发射参数分析方法准确度较低、易受环境影响,模型预测准确度不高的问题,对机械密封声发射信号进行了如下处理:首先对数据进行小波降噪处理,再对降噪信号进行小波包分解,对各频带的子信号进行特征抽取,得到大量声发射特征,再利用KPCA对特征矩阵降维处理,得到贡献率高的少量特征,再利用马氏距离进行特征融合,最后利用QPSO算法优化SVR支持向量回归进行寿命预测。
3 声发射信号处理
3.1 信号的特征提取
由于有环境噪声的产生,从实验采集的样本可以看出低频部分有很多毛刺。为削弱背景噪声的影响,突出有用信号,对样本数据采用小波降噪,滤掉了低频噪声信号,保留了高频有用信号,降噪效果非常明显,如图4所示。

图4 降噪前后声发射信号对比
由于表征声发射信号特征众多,以及缺乏明确的退化指标,故采用特征融合的方式建立所需的退化指标。首先对每个频带的子信号提取表1中的特征,共计得到120个特征。然后将得到的高维特征进行降维处理,通过核主成分分析(KPCA)把贡献率大于90%的特征提取出来,特征如图5所示。

图5 KPCA优化特征
为了得到唯一的退化指标,利用马氏距离对KPCA后的特征进行融合。经过磨合期和平稳期后机械密封性能急剧退化,该过程随时间变化,如图6所示。

图6 融合后的马氏距离
对剩余3组全寿命数据采用同样的信号处理方法,得到相应的退化指标。
3.2 寿命预测
将退化指标分为训练样本集1、2、3和测试样本集4。利用训练样本集对量子行为粒子群算法优化支持向量回归机(QPSO-SVR)进行训练,再利用测试样本集对该模型的预测能力和有效性进行校验。其中设置QPSO-SVR的种群数量为30,迭代次数为300,选择RBF核作为SVR的核函数,确定惩罚参数c和核函数参数的取值范围均为[0,100]。通过样本集的训练,得到最终的惩罚参数c为0.324,核函数参数g为0.841。
经过计算,得到如表2所示预测模型对训练数据的预测误差。表中数据表明,预测误差较小,预测结果较好。将预测样本集输入QPSO-SVR模型,得到表2所示结果,证明了该模型有着较高的准确度。

表2 QPSO-SVR模型预测结果
为了进一步说明QPSO-SVR模型在参数优化和预测准确度方面的效果,建立普通的SVR模型进行寿命预测。人为设定惩罚参数c为1,核函数参数g为1.2,采用上述预测过程,同样训练样本为1、2、3,测试样本为4。QPSO-SVR和SVR预测曲线如图7所示,绝对误差对比图如图8所示,结果如表3所示。经过QPSO改进后的SVR预测模型比普通的SVR预测模型更加接近真实的寿命退化过程,预测准确度高于普通的SVR预测模型。
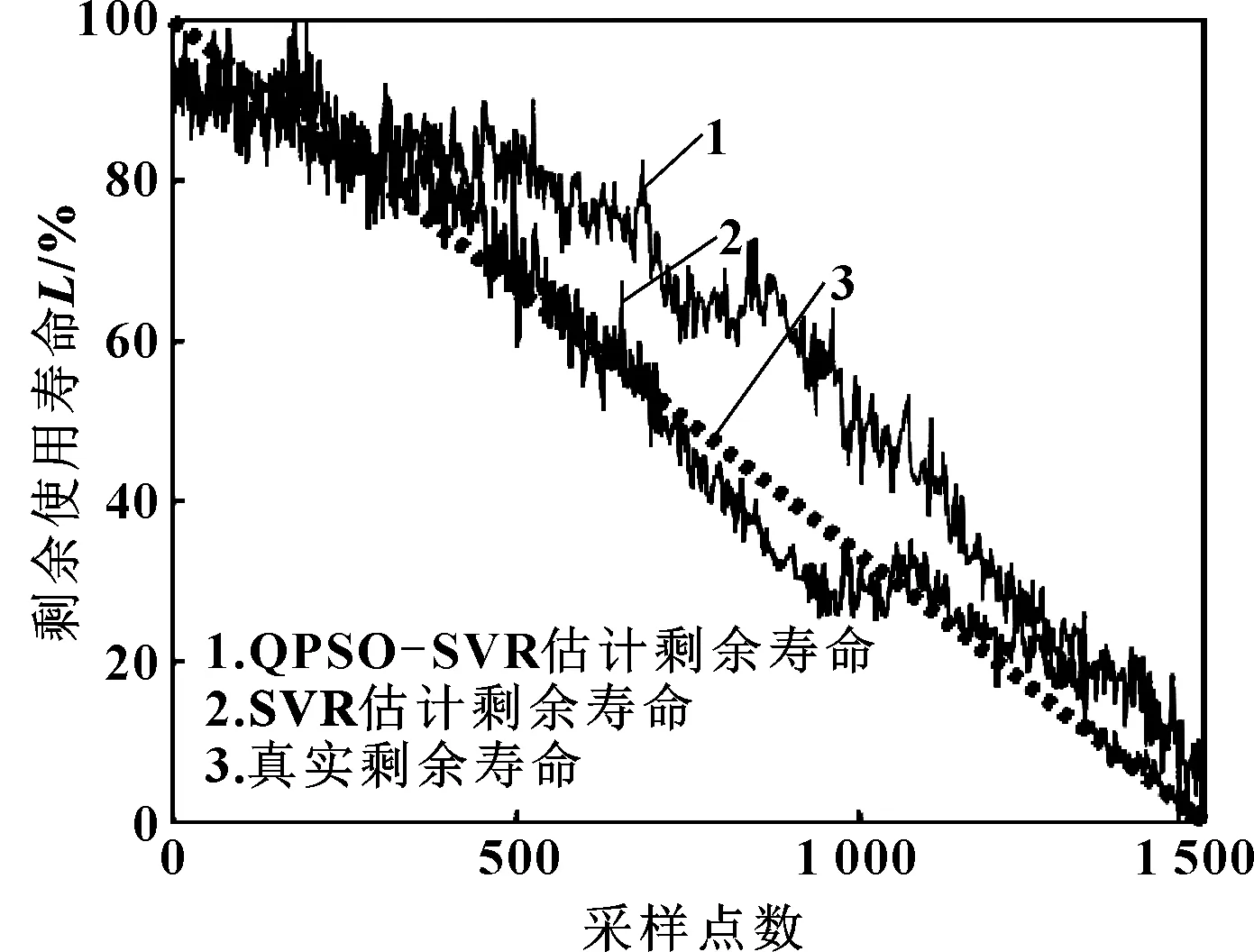
图7 QPSO-SVR与SVR估计剩余寿命以及真实寿命对比

图8 QPSO-SVR与SVR估计剩余寿命的绝对误差对比
表3 QPSO-SVR和SVR模型预测结果
Table 3 Prediction results of QPSO-SVR model and SVR model

名称SVRQPSO-SVR惩罚参数10.324核函数参数1.20.841相对误差11.84%4.7%
为了证明QPSO-SVR模型在有着良好的泛化能力,在原声发射信号的基础上加入高斯白噪声,用训练好的QPSO-SVR模型和SVR模型进行寿命预测。QPSO-SVR和SVR预测曲线如图9所示,绝对误差对比图如图10所示,结果如表4所示。经过QPSO改进后的SVR预测模型比普通的SVR预测模型具有更高的精度。通过原信号和加噪信号两组不同信号的预测结果对比,说明了QPSO-SVR模型不仅有着更高的精度,同时有着良好的泛化能力。
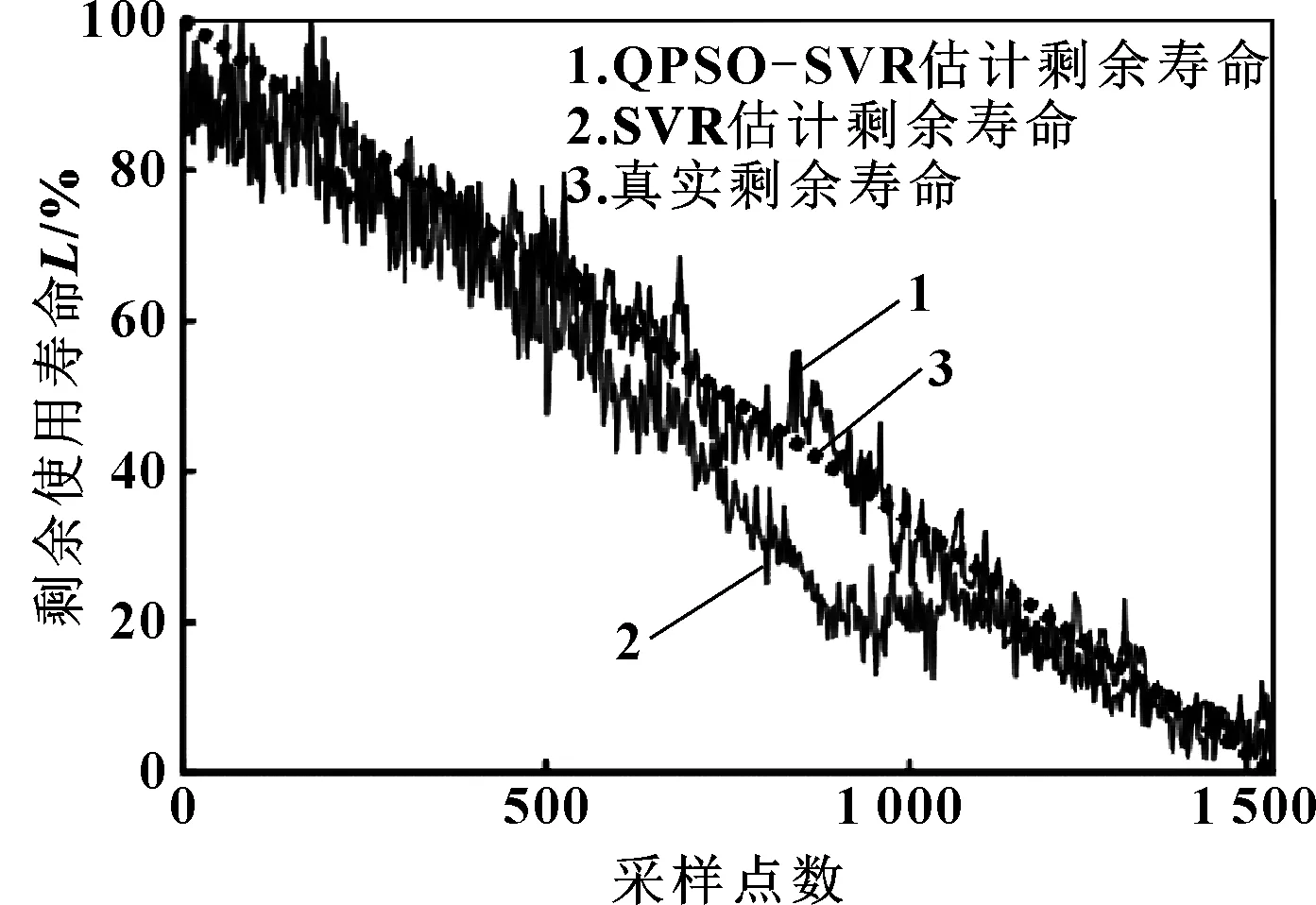
图9 加入高斯噪声后QPSO-SVR与SVR估计剩余寿命以及真实寿命对比

图10 加入高斯噪后QPSO-SVR与SVR估计剩余寿命的绝对误差对比
表4加噪声后QPSO-SVR和SVR模型预测结果
Table 4 Prediction results of QPSO-SVR model and SVR model after adding Gauss noise
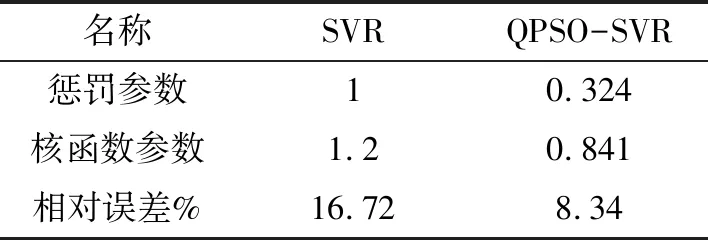
名称SVRQPSO-SVR惩罚参数10.324核函数参数1.20.841相对误差%16.728.34
4 结论
(1)采用多种统计特征,结合特征之间的优缺点,利用KPCA进行特征优化,得到主要的特征成分。通过马氏距离融合出退化指标,表征机械密封性能退化过程,简化了模型训练的输入参数。
(2)对比普通SVR模型和QPSO-SVR模型的效果,结果表明,QPSO-SVR避免了参数设定的盲目性,应用QPSO方法寻找到全局最优的参数值,模型有着较好的泛化能力和预测准确度,得到了较好的回归模型,对金刚石涂层机械密封寿命预测具有一定意义。
