一类高阶分数阶微分方程边值问题的Lyapunov不等式研究

杨子发， 马德香

(华北电力大学 数理学院, 北京 102206)

对于下列边值问题：

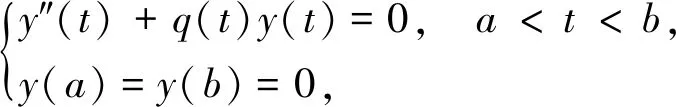
(1)

其中q(t)是实连续函数。在文献[1]中有如下结论：若式(1)有非零解，则下列Lyapunov不等式成立:

(2)

Ferreira[2]将上述结论推广到一类含Caputo导数的分数阶微分方程的边值问题：

(3)

(4)

显然，当α=2时，式(4)即为式(2)。

自文献[2]以后，分数阶微分方程的Lyapunov不等式被广泛研究,如Ferreira[3]得到了下列微分方程边值问题的Lyapunov不等式:

(5)

(6)

的存在性。Surang Sitho等[5]研究了Lyapunov不等式

(7)

的存在性。Nassir Al Arifi等[6]研究了Lyapunov不等式

(8)

的存在性。Yang Liu等[7]研究了Lyapunov不等式

(9)

的存在性。更近的结果见文献[8-10]。

受以上文献的启发，本文研究下列高阶分数阶微分方程边值问题的Lyapunov不等式:

(10)

1 准备工作

为方便起见，首先给出Riemann-Liouville分数阶积分和Riemann-Liouville分数阶导数的定义。

定义1 函数u(t)的α阶Riemann-Liouville分数阶积分定义如下：

定义2 函数u(t)的α阶Riemann-Liouville分数阶导数定义如下：

其中α>0，n=[α]+1，[α]表示不大于α的最大整数。

由定义1和2，易得下列结论：

(13)

2 主要结果

(14)

(15)

由u(i)(0)=0可知Ci=0，i=2，3，…，n，则

(16)

结论得证。

引理2 当β∈[0，1]时，G(t，s)有如下性质：

(i)G(t，s)≥0，(t，s)∈[0，1]×[0，1]；

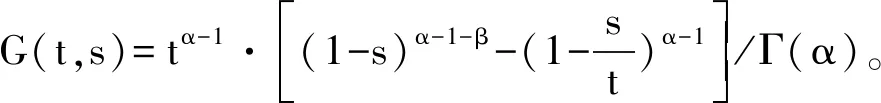
(17)

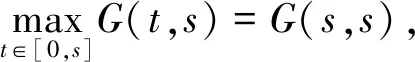
(18)

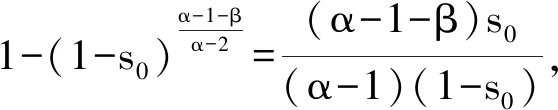
结论得证。

定理1 当β∈[0，1]时，若式(10)有非零解u(t)，则

(19)

定理得证。

引理3 当β∈[α-1，1]时，G(t，s)有如下性质：

(i)G(t，s)≥0，(t，s)∈[0，1]×[0，1]；

(ii) ∀s∈[0，1]，G(t，s)≤G(1，s)，t∈[0，1]；

证明(i)的证明同引理2(i)，略。

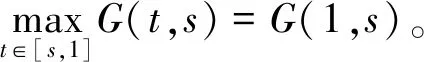
(20)

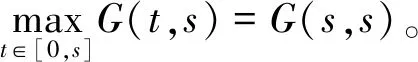
(21)

由式(20)和(21)知∀s∈[0，1]，G(t，s)≤G(1，s)，t∈[0，1]。结论得证。

结论得证。

定理2 当β∈[1，α-1]时，若式(10)有非零解u(t)，则

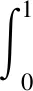
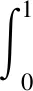
(22)

定理得证。

推论1 若微分方程边值问题

存在非零解u(t)，则

证明在定理1中取α=n，β=0，则由定理1的结论可得推论1成立。

推论2 若微分方程边值问题

存在非零解u(t)，则

证明在定理2中取α=n，β=n-1，则由定理2的结论知推论2成立。

3 应 用

3.1 特征值问题

讨论下列特征值问题.

(23)

其中n≥3，α∈(n-1，n]，β∈[0，α-1]。

由定理1与定理2，可得到下列结果。

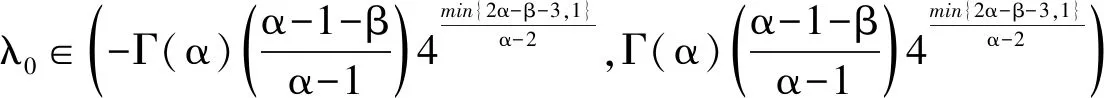
(ii)证明同(i)，略。

3.2 Mittag-Leffler函数的实根

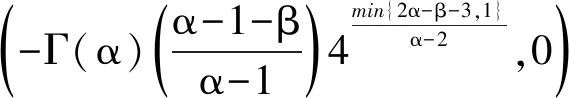
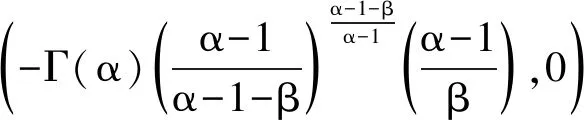
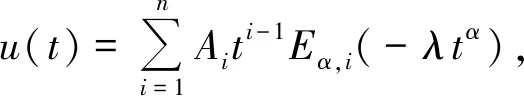
(ii) 证明同(i)，略。