基于蚁群算法的QoS路由模型的设计与优化

高新成， 刘德聚， 王莉利， 马树轩

(1.东北石油大学 现代教育技术中心， 黑龙江 大庆 163318; 2.东北石油大学 计算机与信息技术学院， 黑龙江 大庆 163318)

随着计算机网络的飞速发展，当前网络的多样化应用对网络传输的高性能和高质量提出了更高的需求。传统网络采用“尽力而为”的传输方案很难保证数据的传输质量，还会造成网络资源的浪费，因此必须要对网络进行优化，使其在满足多约束的前提下保障网络资源的最大化配置[1-2]。QoS路由就是典型的一种路由优化手段，它不仅能保证重要的业务数据进行及时可靠地传输，避免发生延迟和丢弃现象，同时还能保证网络的高效流通[3]。QoS路由问题属于特殊的组合优化问题，用传统的数学规划和统筹的思想难以有效解决。通过研究发现，使用蚁群算法等元启发式算法解决QoS路由问题已经成为当前网络优化领域的热点之一[4-8]。本文以蚁群算法解决网络路由问题为研究内容，实现基于蚁群算法在网络路由中的应用。

1 蚁群算法模型

求解规模为n个城市、m只蚂蚁的TSP问题，建立蚁群算法模型[9]。模型符号描述如下：

模型算法对每只蚂蚁的行为要求如下：

(1)使用各条路径上的信息素浓度作为指导值，通过计算各条可选路径的转移概率来决定下一步的行进方向；

(2)本次循环已经走过的路径禁止作为下一次被选择的路径，使用一个禁忌表(tabu list)来实现；

(3)每次循环结束，根据得到的路径长度来指导信息素的释放量，并根据更新规则完成走过路径上的信息素浓度的更新。

1.1 转移概率

每个蚂蚁个体在开始进行搜索时，由于每条路径上的信息素浓度都为设定的初始浓度，即πij(0)=C。蚂蚁k(k=1,2,…,m)在搜索前进的过程中，通过各条可选路径上的信息素浓度来决定下一次转移的方向。在t时刻，位于某一城市的蚂蚁k一次只能选择一个城市作为下一个目标城市，n次后返回起点完成一次循环。那么在t时刻，蚂蚁k从城市i移动到城市j的转移概率公式为

(1)

allowedk={C-tabuk}表示在t时刻蚂蚁可以选择的城市集合，即未访问的城市集合；tabuk(k=1,2,…,m)记录蚂蚁k已经走过的城市集合；α为信息启发因子，表示存留下来的信息素相对重要程度；β为期望启发因子，表示能见度的相对重要程度。

1.2 信息素的更新

为了避免信息素含量过多而影响启发信息发挥作用，所以要求每只蚂蚁完成对n个城市的遍历后必须严格依照某个规则对路径上的信息素进行更新，这样才能保证随着时间的推移，以前留下的信息素会逐渐消失。信息素的更新公式为

πij(t+n)=(1-ρ)πij(t)+Δπij(t)，

(2)

(3)

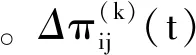
(4)

式中Q为常数，表示信息素增加的强度；Lk表示蚂蚁k完成此次循环后经过的路径总长度。

2 基于ACO的QoS路由模型设计

2.1 QoS路由问题描述

网络模型通常抽象为一个无向赋权图G=，其中V表示无向赋权图中的所有节点组成的集合，E表示无向赋权图中节点间链路的集合，其中每一条链路代表相邻两节点间的直通路径。QoS路由定义为从源节点到目的节点间找出一条满足QoS约束，且代价最小的最佳路径。实际问题中通常使用延时、延时抖动、带宽、费用、丢包率5种度量参数作为网络中的QoS约束[10-11]。对网络拓扑中的节点V和链路E定义描述如下：

(1)对于任意网络节点n∈V，定义延时、延时抖动、丢包率如下所示(R+表示非负实数集)。

延时函数delay(n):E→R+，表示IP包每次在网络中传送花费的平均时长。

延时抖动函数delay_jitter(n):V→R+，表示IP包传送时间的长短变化。延时和延时抖动均可能会造成网络传输质量的下降。

丢包率函数packet_loss(n):V→R+，表示在传送的过程中可能会出现IP包的损坏或丢失，该参数值越高表示数据受到的损害概率就越大。

(2)对于任意网络中链路e∈E，定义延时、延时抖动、带宽、费用4种度量，如下所示。

延时函数delay(e):E→R+。

延时抖动函数delay_jitter(e):E→R+。

带宽函数bandwidth(e):E→R+。

费用函数cost(e):E→R+。

(3)给定一个源节点和目的节点，通过算法如果能找到一条费用最小的路径即路由请求L，同时满足下述条件，则该条路由请求可被接受。

带宽约束：在路由请求L上的每条链路上，bandwidth(e)≥B。

丢包率约束：在路由请求L的每个节点n上，packet_loss(n)≤PL。

D、DJ、B和PL分别表示QoS路由中对延时、延时抖动、带宽、丢包率的约束值；VL为路由请求L上的节点集合，EL为路由请求L上的链路集合。

2.2 QoS路由模型建立

QoS路由模型定义G中节点总数为n=|V|，给定源节点s∈V，目的节点d∈|V-|s||[12]。对无向赋权图G中任意一个节点n∈V，定义3种度量属性:延时函数delay(n)、延时抖动函数delay_jitter(n)和丢包率函数packet_loss(n)。对于途中任意一条链路e∈E，定义4种度量属性，即延时函数delay(e)、延时抖动函数delay_jitter(e)、带宽函数bandwidth(e)和费用函数cost(e)。

路径p(s,d)上的总延时函数定义为

路径p(s,d)上的最小带宽定义为

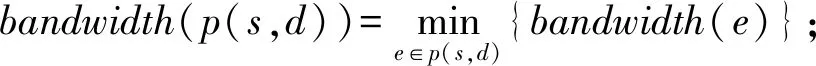
路径p(s,d)上的延时抖动定义为

路径p(s,d)上的丢包率定义为

路径p(s,d)上的费用定义为

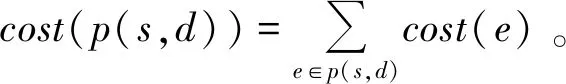
路径p(s,d)表示源节点s与目的节点d之间所有满足QoS约束的路径，则QoS路由问题为找到满足条件delay(p(s,d))≤D、delay_jitter(p(s,d))≤DJ、bandwidth(p(s,d))≥B和packet_loss(p(s,d))≤PL的最佳路径。

2.3 基于ACO的QoS路由算法

应用蚁群算法模型求解QoS路由算法的具体实现过程如下。

Step1:给出指定网络拓扑图，设置图中各节点和每条边的参数值，以及QoS约束中的D、DJ、B、PL的取值，并对蚁群算法中相关参数进行如下设置。

Set t=0

NC=0 {NC是循环计数器}

NC_max，m {NC_max为循环最大次数，m为蚂蚁个数}

W=s {当前节点为起始点}

Path=s {路线初始化}

PD=0 {路线延时初始化}

cost=0 {路线费用初始化}

Step2：寻找蚁群中每只蚂蚁寻找的最优路径。

For NC=1 to NC_max

For k=1 to m

初始化禁忌表tabu及相应参数；

寻找可选节点集；

计算蚂蚁k向各可选节点的转移概率；

用转盘赌法确定转移节点j；

If节点j是目的节点d

则清空所有tabu列表，进行下一只蚂蚁的遍历；

Else

计算出蚂蚁k移动到节点j之后的D、DJ和B等参数进行比较；

If不满足约束条件

则重新选择节点j；

Else

将蚂蚁k移动到节点j，将节点j插入tabuk(s)，并进行信息素浓度的更新；

End

End

End

End

Step3：迭代寻找最短费用的路径cost，输出最短费用的路径path。

cost=costs(1,1,1) {最短费用路径初值}

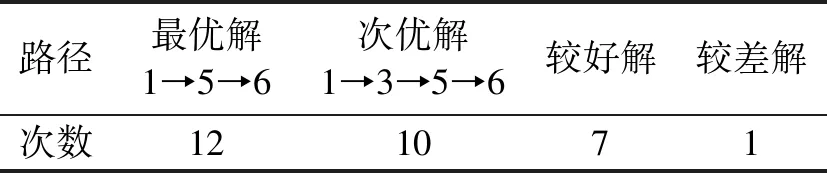
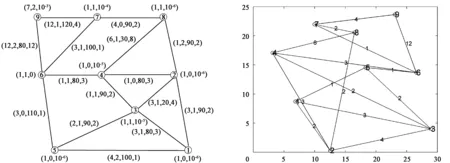
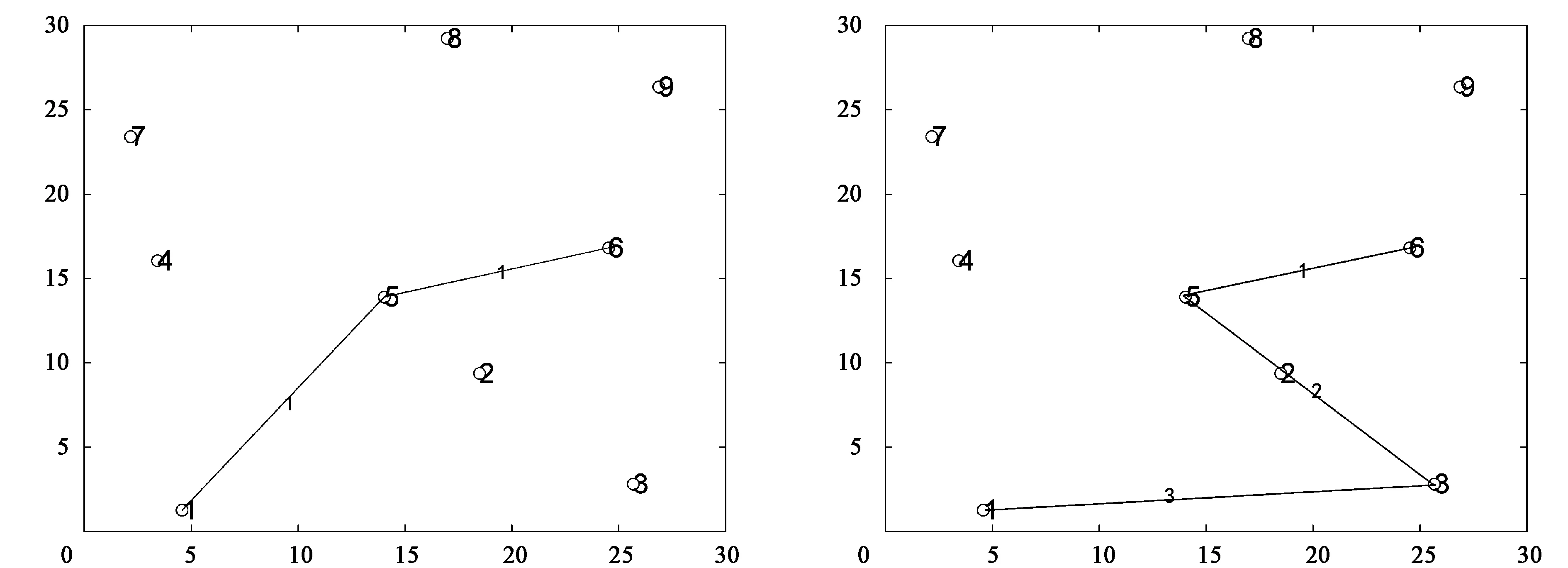
if costs(p,k,m)

cost=cost(p,k,m)

path=routes{p,k,m} {找出最短费用路径}

3 仿真实验与优化分析

3.1 实验参数设置

针对QoS路由模型进行仿真实验，预定网络拓扑如图1所示。图中每个节点特征用三元组(d,DJ,PL)表示，即延时、延时抖动、丢包率，每一条链路特征用四元组(d,DJ,B,cost)表示，即延时、延时抖动、带宽、费用[10]。参数设置如表1、表2所示。

表1 蚁群算法参数

表2 QoS路由参数

3.2 实验结果分析

实验给定的路由请求为源节点1到目的节点6，实验中预定网络拓扑的建立是通过邻接矩阵的形式绘制，如图1所示。程序运行绘制的实验拓扑如图2所示，其中节点间链路的数值为该条链路的费用。实验运行共30次，产生最优解(1→5→6)的仿真结果如图3所示。产生次优解(1→3→5→6)的仿真结果如图4所示。

表3 实验运行结果

图1 预定网络拓扑图 图2 实验网络拓扑图

图3 最优路径(1→5→6) 图4 次最优路径(1→3→5→6)

运行程序30次所得的仿真结果，如表3所示。

通过算例仿真实验结果表明：本文设计的基于蚁群的QoS路由算法在实际网络路由中能够准确发现最优解和次优解，同时也验证了该算法在求解QoS网络路由问题上应用效果良好。

3.3 参数优化分析

在实验过程中，针对影响算法解质量的参数进行不同的设置并进行仿真实验，实验参数的不同取值仿真结果，如表4所示。

通过实验结果可知，蚁群算法参数值设置对精确求解影响较大，优化参数选择能够提高最优解和次优解的出现概率，保证质量较差解出现的概率最小，具体参数优化分析如下：

(1)信息启发因子α的取值越大表示蚂蚁个体选择之前经过的路径的概率就越高，降低算法搜索路径的随机性，加快了算法的收敛速度，导致算法容易过早的进入局部最优状态。

(2)期望启发因子β的取值越大表示蚂蚁选择局部最优路径的概率就越高，降低算法搜索的随机性，同时造成算法的收敛速度加快，使算法容易进入局部最优的状态。

(3)信息素挥发度ρ的取值过大时，将会导致信息素消失过快，容易导致之前选择过的路径被再次搜索到，造成算法搜索随机性和全局搜索能力降低。当ρ的取值过小时，随着时间推移信息素含量变化很小，算法搜索的随机性和全局搜索能力虽然有所提高，但会造成算法的收敛速度降低。通过实验反复测试得到ρ的取值在0.5～0.9之间最佳。

表4 不同参数值得仿真结果

(4)蚂蚁个体数m取值较大，信息素的正反馈效应得不到很好体现，虽能提高搜索的随机性，但收敛速度得不到保证；反之，m取值较少，在解决规模较大的问题时，虽然会加快收敛速度，但会导致算法搜索的随机性下降，造成算法稳定性的降低，提高了算法早熟的概率。

4 结 论

针对蚁群算法求解QoS网络路由优化问题，通过分析QoS网络路由具体问题，建立相应QoS路由模型，并进行仿真实验。实验结果表明，本文提出的基于蚁群算法解决QoS路由问题的方法是有效的，并具有很好的求解效果。同时对蚁群算法信息启发因子、期望启发因子、信息素的挥发程度等参数取值进行优化分析，给出最佳取值范围，提高了求解精度与运算效率。