数学探究 乐在其中

江苏省如皋中学高二(1)班 (邮编：226500)

江苏省如皋中学 指导老师 范栋志 (邮编：226500)

笔者对2018年南通市高三第二次调研试题第13题有关向量数量积的问题进行了深度探究.从最初的思考起步，扣住关键，不断优化，自我设问，大胆尝试，逐层深入.在探究的过程中不断完善知识网络体系，更深层次地认识到基础知识、基本方法、基本能力在解题中的重要作用.在探究的过程中有烦恼，更有乐趣，并乐在其中.

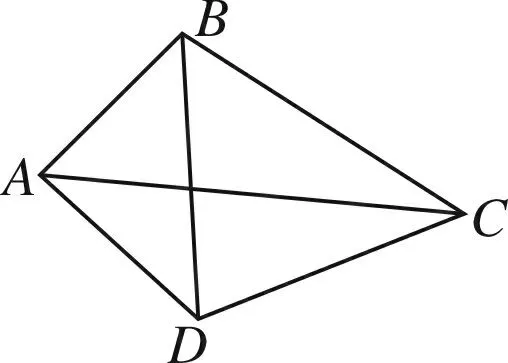
图1

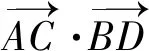
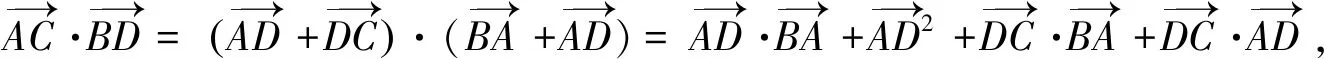
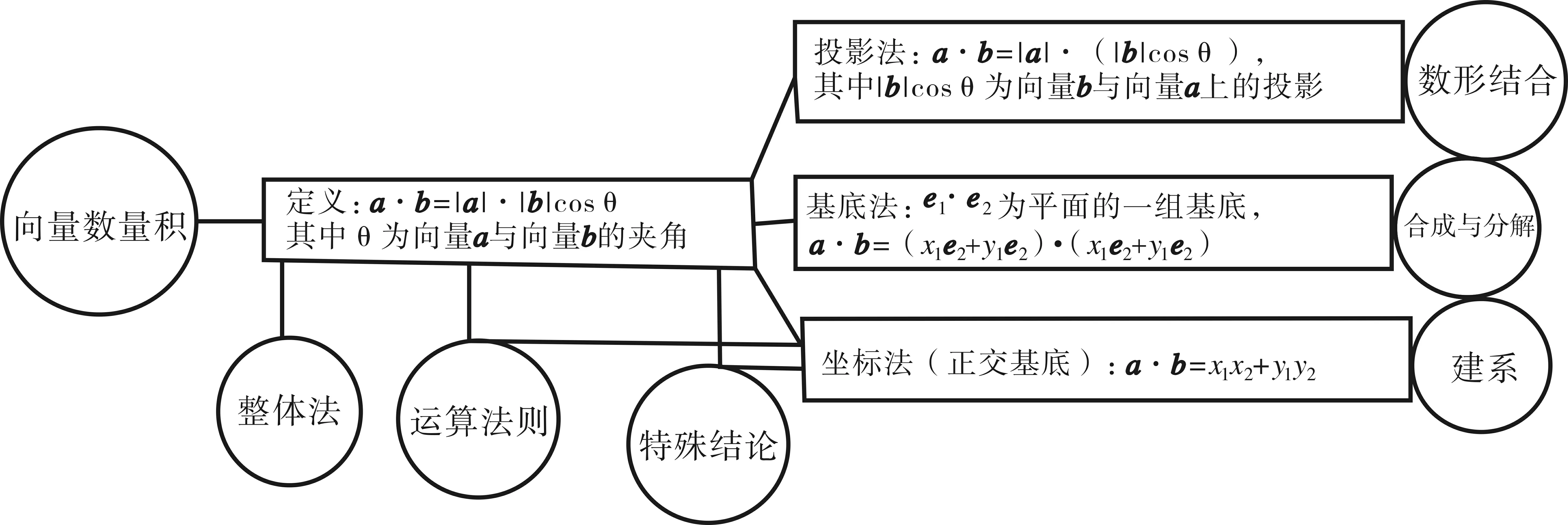
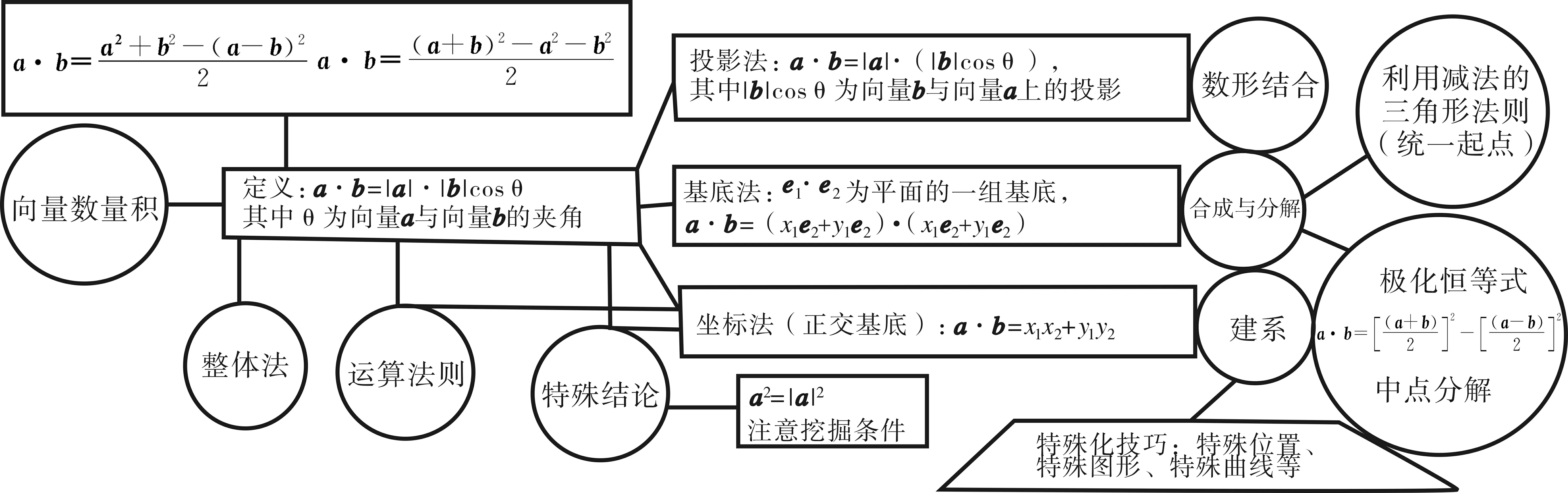
自我梳理向量数量积有多种运算方法，破解渠道，值得细细思考.下面是向量数量积的知识网络图.

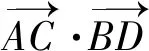
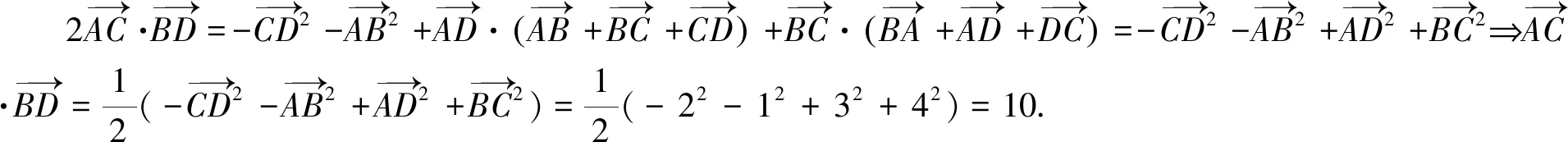
优化二上述方法先合成与分解，再利用数量积的定义，结合余弦定理，化简要使得两向量有一个共同的点，这样夹角的余弦才能借助余弦定理求得.据此可在第一次合成与分解时实现，避免二次麻烦.

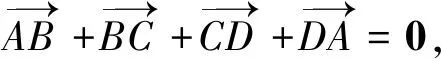
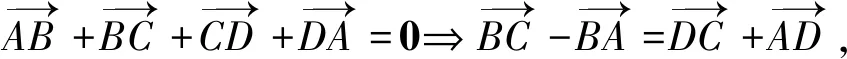
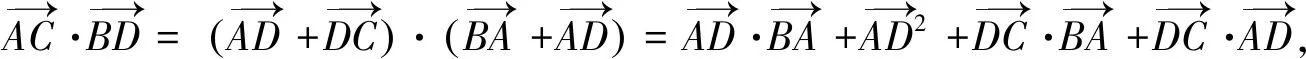
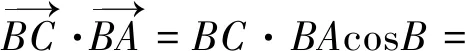
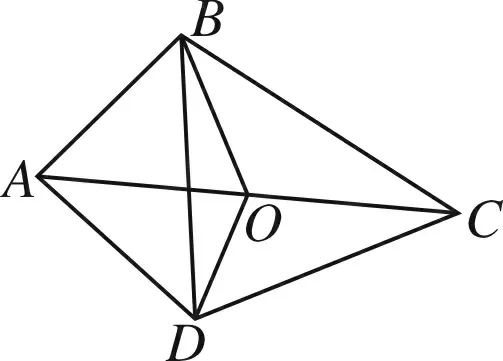
图3

优化七从上述的解题过程可以发现，O为平面上的任意一点，那么可以尝试在四边形的四个顶点之中选择将更简单.选择点A进行尝试.

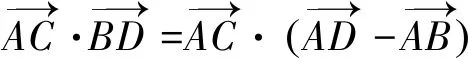
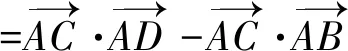
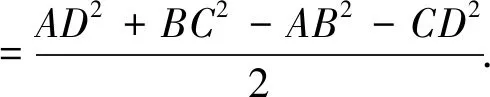
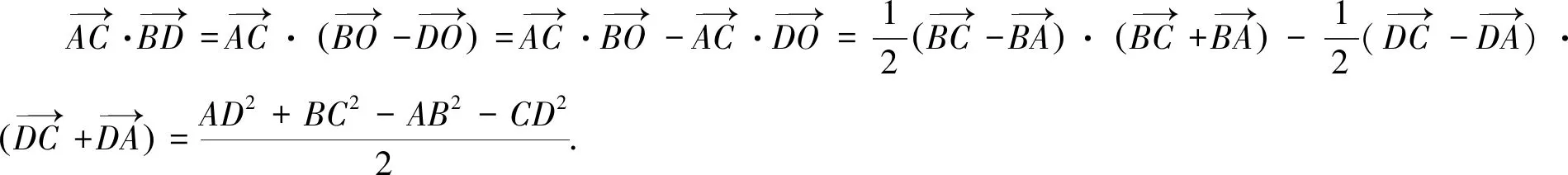
注一次次的深入思考过程中，解法更灵活，既简化了运算，更渗透了本质，真是美的享受.

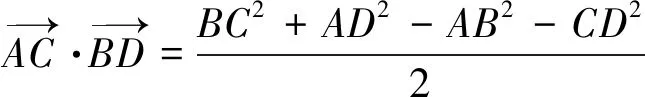
优化九坐标法

设∠ABC=θ，以B为坐标原点，BC边所在直线为x轴，建立平面直角坐标系xOy，

则A(cosθ，sinθ) ，C(4，0).设D(x,y)，

则由AD=3，CD=2，得

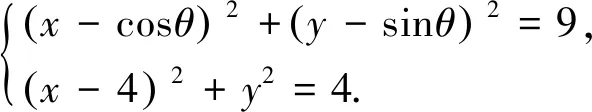
将两式相减，即得(4-cosθ)x-ysinθ=10，

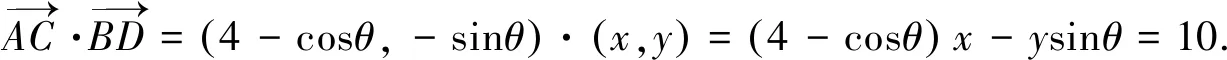
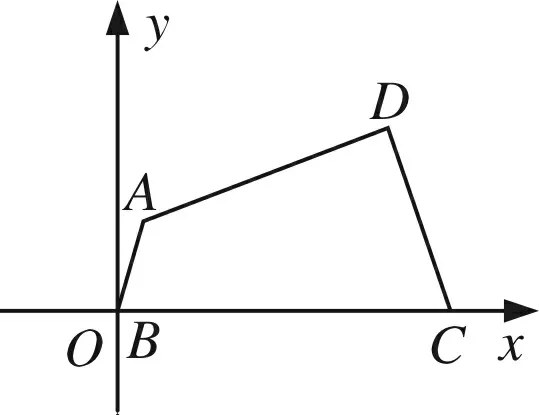
图4

注经分析可知本题的图形是一个动态图形，而解题目标是求定值，故可采用特殊化策略，如取θ=90°.

优化十

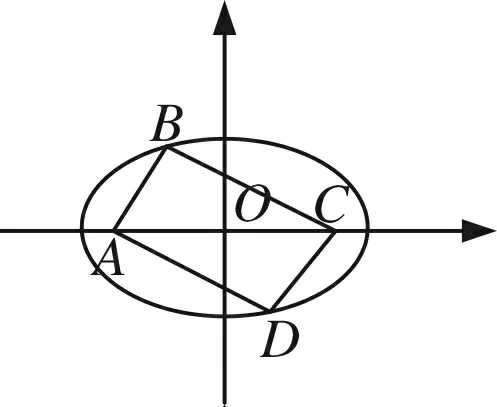
图5

因为AB+BC=CD+DA=5,不妨构造焦点在x轴上的椭圆(如图)，

设B(x1,y1),D(x2,y2)，则AB=1,BC=4,CD=2,DA=3，利用焦半径公式，得

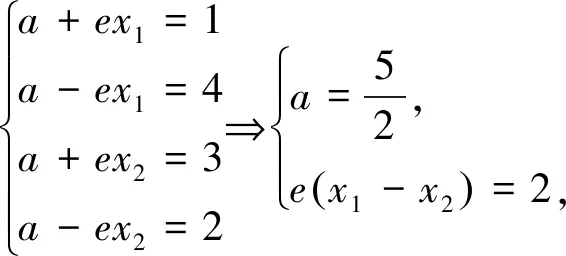
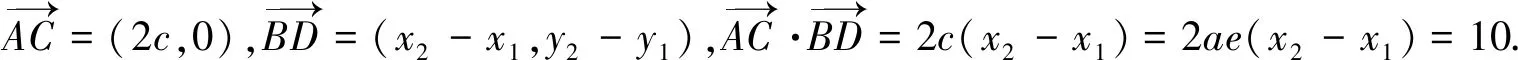
自我再梳理通过上述优化的过程，有很多感受，探究优化中学到很多新的技能，对今后的学习有很大的帮助，下面来完善一下数量积最初的知识网络图吧.

基本方法的理解与灵活运用还需在解题过程中得到深刻，解题能力的提升必须依靠解题，笔者百度了下面几道类似的题目，牛刀小试，希望能够日渐锋利.

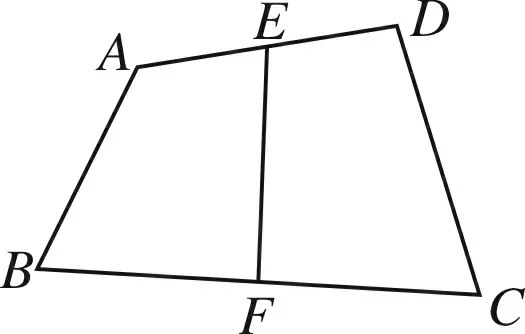
图6

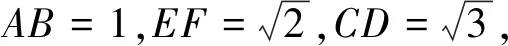
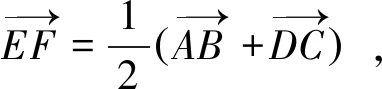
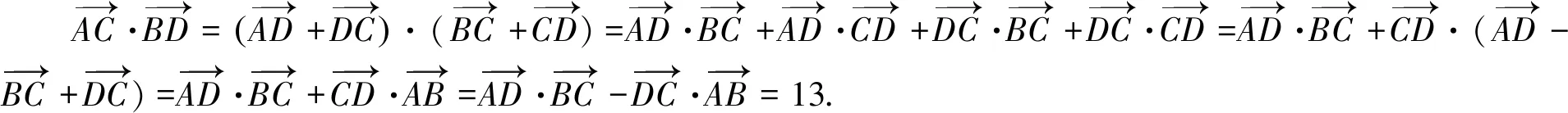
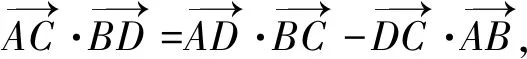
(1)

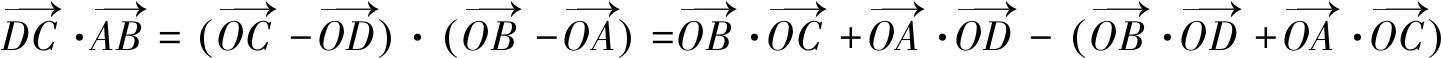
(2)

(3)

只要将(1)-(2)可得(3)

方法三对角线定理

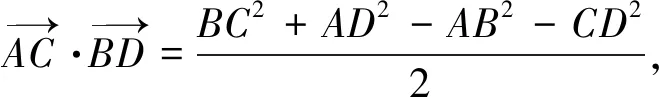
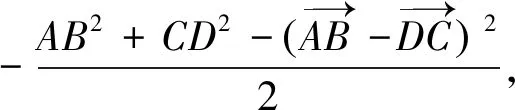
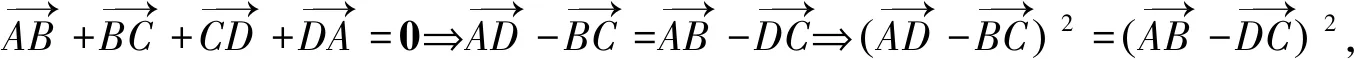
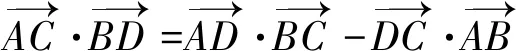
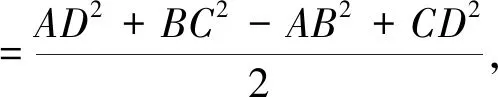
通过牛刀小试题的处理，进一步加深了数量积相关知识的理解，熟练应用数量积知识网络图处理数量积相关问题，使知识方法进一步系统化、网络化，让思维可视，让发散更自然.我愿意在数学探究这条道路上一直走下去，享受其中的乐趣.