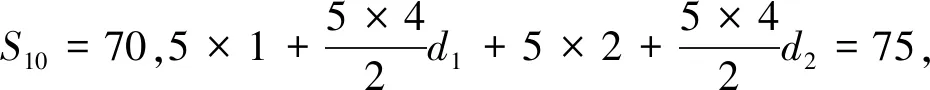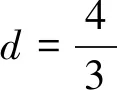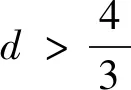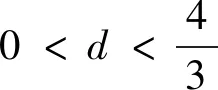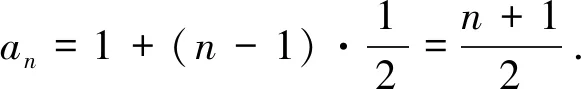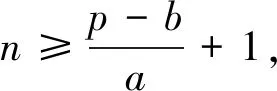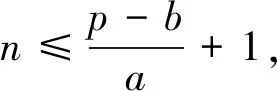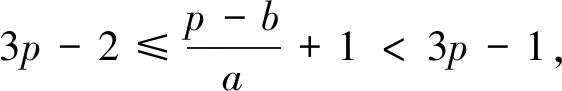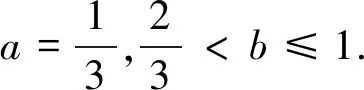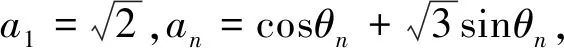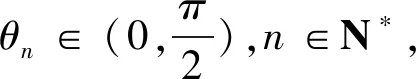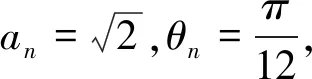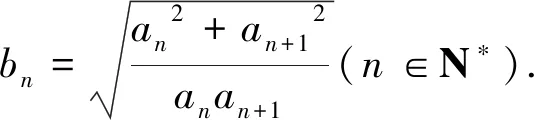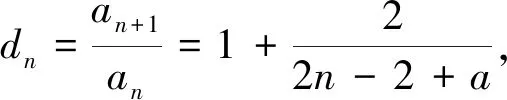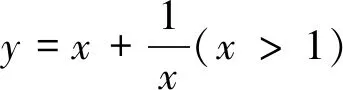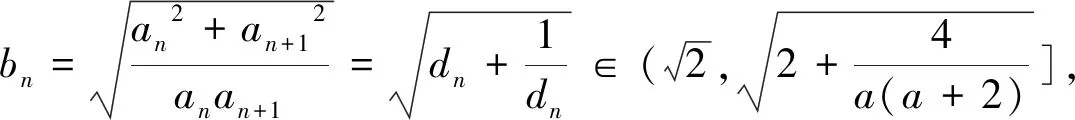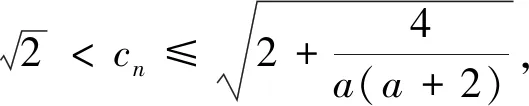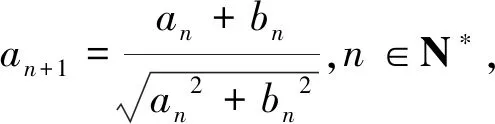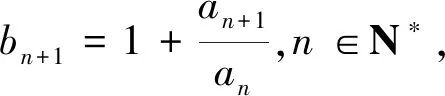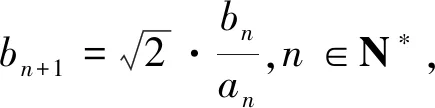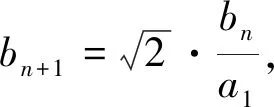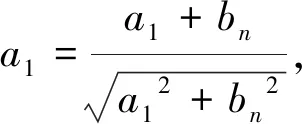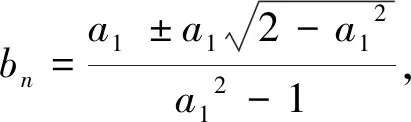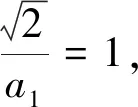与常数列相关的两个结论的妙用

江苏省姜堰中学数学组 (邮编：225500)

众所周知，如果一个数列既是等差数列又是等比数列，那么它一定是非零常数列.其实，以下两个与常数列相关的结论，看似简单明了，解题中如果巧妙运用，常可以另辟蹊径.

结论1 设A、B是已知常数，若无穷等差数列{an}满足：A

结论2 设A、B是已知正常数，若无穷正项等比数列{an}满足：A

例1 (2016年江苏省竞赛初赛题)已知数列{an}的奇数项依次构成公差为d1的等差数列，偶数项依次构成公差为d2的等差数列，且对任意n∈N*，都有an

解析依题意，a2n-1=a1+(n-1)d1,a2n=a2+(n-1)d2,a2n+1=a1+nd1,

由a2n-1

根据结论1可知，等差数列{(d2-d1)n}为常数列，所以d2=d1，

例2 (2018年南京高三三模试题)已知数列{an}是等差数列，a1=1，对任意正整数n，有an

解析设an=1+(n-1)d,d>0，代入an

(2d2-d)n>d2-3d+1，且(d-2d2)n>2d2-d-1均对任意正整数n恒成立，

例3 (2013年连云港高三期末试题)已知数列{an}的通项公式an=a(n-1)，问是否存在实数a、b，使得对于任意正整数p，数列{an}中满足an+b≤p的最大项恰为第3p-2项？若存在，求出a、b的取值范围；若不存在，请说明理由.

解析因为an=a(n-1)，由an+b≤p得a(n-1)+b≤p，

若a=0，不合题意，舍去；

因为{an}中满足an+b≤p的最大项恰为第3p-2项，

根据结论2可知，数列{cn}是常数列，其公比q的值为1.

解析(1)证明过程略；

又由于

根据结论2可知，{an+1}是常数列，从而等比数列{an}是常数列，各项为a1，