由一个45度角想到的
2019-04-18江苏省昆山市费俊龙中学邮编215300
江苏省昆山市费俊龙中学 (邮编:215300)
关键字 45度;旋转;相似;全等
45度角是初中几何经常碰到的特殊角,遇到45度角,往往会联想到等腰直角三角形、正方形等特殊的几何图形,并进而衍生出一系列有意思的结论.在平时的解题中,如果我们做到解法多样,同时找到题目的原始模型,并进行适当的变式训练,掌握正确有效的解题方法,相信就可以避免题海战术,从而增加解题的乐趣.
1 问题原型
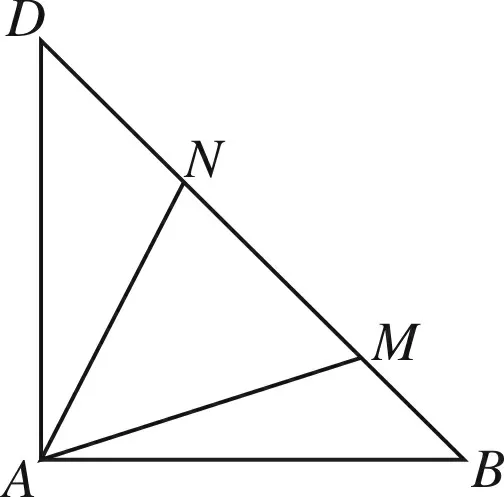
图1
例1 如图1,已知等腰直角三角形ABD中,点M和点N在斜边BD上,且满足∠MAN=45°,求证:BM2+DN2=MN2.
证法1 旋转法
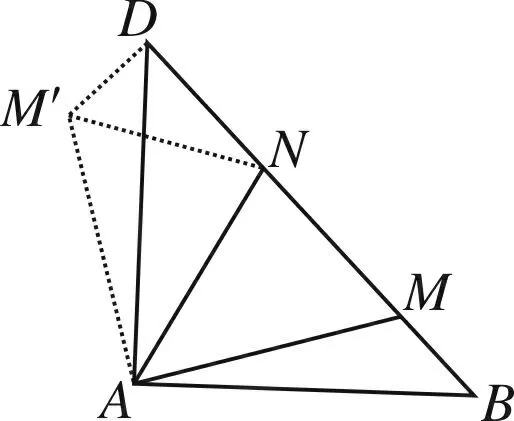
图2
如图2,将△ABM绕点A逆时针旋转90度得到△ADM′,可得△ABM≌△ADM′,所以∠ADM′=∠B=∠ADB=45°,故∠M′DN=90°,所以DM′2+DN2=M′N2,因为∠BAM+∠DAN=45°,所以∠DAM′+∠DAN=45°,即∠M′AN=45°,由SAS可得△M′AN≌△MAN,所以BM=DM′,MN=M′N,故BM2+DN2=MN2.
证法2 对称法
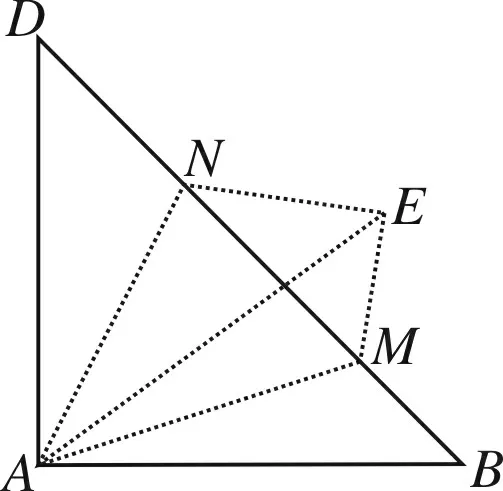
图3
本题是等腰直角三角形及正方形45度角模型中的一道经典题目,下面笔者想针对这一模型对例1做进一步的推广和研究,我们发现有关这个模型的结论可以说是“源源不断,用之不竭”.
2 拓展1
本例主要是借助与正方形有公共点的45度角模型,运用旋转的相关知识,抓住旋转前后的一些对应关系来挖掘出一系列结论.
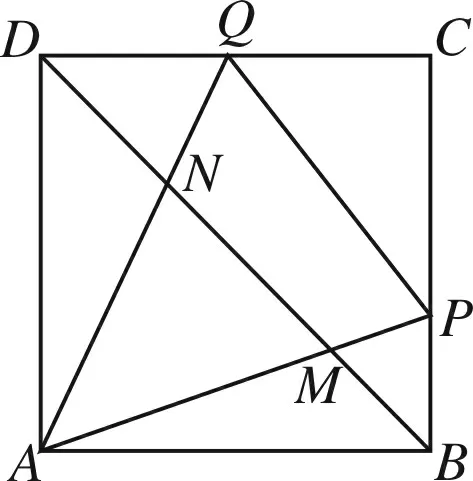
图4
例2 如图4,如果将等腰直角三角形ABD沿BD翻折,我们可以得到正方形ABCD,若∠MAN=45°,延长AM与BC交于点P,延长AN与CD交于点Q,设正方形边长为1,我们可以进一步证明以下结论:
(1)BM2+DN2=MN2;
(2)△CPQ的周长等于2;
研究对象选自2015年12月至2017年12月本院诊治的急性糜烂出血性胃炎大出血患者100例,随机对其进行分组,分成50例研究组和50例对照组,所有患者均知情同意参与本次研究。其中研究组50例患者中男性患者34例,女性患者16例;年龄在52-80岁,平均年龄(69.81±11.2)岁;主要临床表现为呕血和便血。对照组50例患者中男性患者33例,女性患者17例;年龄在51-79岁,平均年龄(68.34±10.93)岁;主要临床表现为呕血和便血。研究组与对照组在性别、年龄以及主要临床表现等方面对比无明显差异,P>0.05,无统计学意义。
(3)PQ=BP+DQ;
(4)点A到线段PQ的距离等于1;
(5)AN=NP;
(6)AM=MQ;
(7)连接MQ,NP交于点O,则AO所在直线垂直于PQ;
(8)△AMN的面积为△APQ面积的一半;
(10)PQ2=2(BM2+DN2).
证明(1)结合例1,易证.
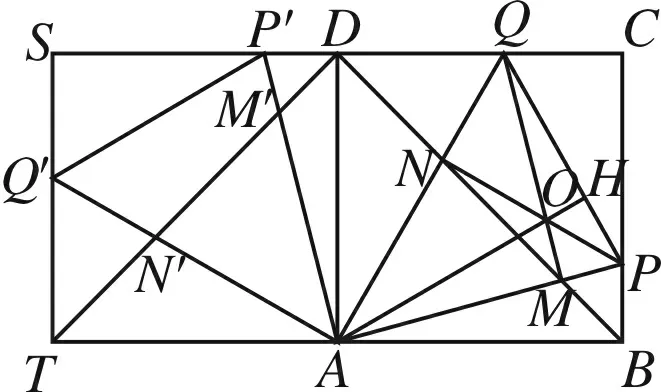
图5
(2)如图5,将正方形ABCD绕点A逆时针旋转90度得到正方形ADST,因为∠PAP′=90°,所以∠PAQ=∠P′AQ=45°,又因为AQ=AQ,PA=P′A,根据SAS可得△PAQ≌△P′AQ,所以P′Q=PQ,所以△PCQ的周长=PC+CQ+PQ=P′S+CQ+P′Q=2.
(3)由旋转的性质可得P′D=BP,PQ=P′Q,因为P′Q=P′D+DQ,所以PQ=BP+DQ.
(4)因为△PAQ≌△P′AQ,所以∠AQP′=∠AQP,同时∠ADQ=∠AHQ=90°,AQ=AQ,根据AAS可得△ADQ≌△AHQ,所以AD=AH=1.
(5-6)因为∠PAQ=∠DBC=45°,故A、B、P、N四点共圆,由此得∠ABD=∠APN=45°,故△APN为等腰直角三角形,即AN=PN,同理可得AM=QM.
(7)设线段PN,QM交于点O,由(5-6)可得AN⊥PN,AM⊥QM,所以点O为△APQ的垂心,根据三角形的三条高交于同一点,可得AO⊥PQ.
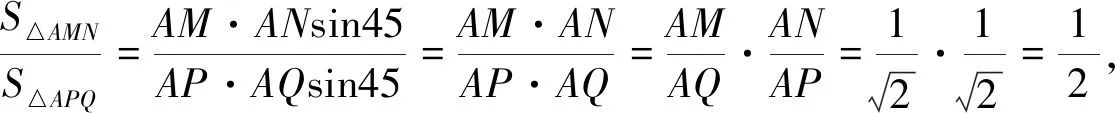
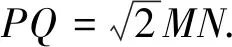
(10)由于BM2+DN2=MN2,因为由(9)得PQ2=2MN2,所以PQ2=2(BM2+DN2).证毕.
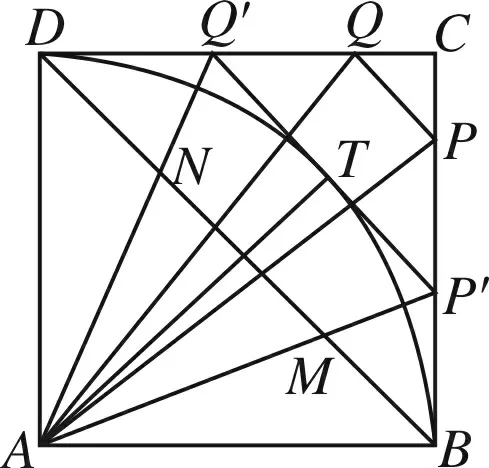
图7
思考接下来我们探究如何寻找点P、点Q,使之符合上述题目条件.如图6,以A为圆心,线段AB长度为半径作圆弧,易知必经过点D,在圆弧上任取一点T,过点T作圆A的切线,根据切线长定理可得PB=PT,QD=QT, ∠BAP=∠TAP,∠DAQ=∠TAQ,易证∠PAQ=45°,反之如图7,若PQ所在直线与圆A相离,做直线P′Q′∥PQ且与圆O相切,可得∠PAQ<∠P′AQ′,故∠PAQ<45°.同理若PQ所在直线与圆A相交,可得∠PAQ>45.
综上我们得到以下结论:当且仅当PQ所在直线与圆A相切时,∠PAQ=45°.
3 拓展2
类似地,等腰直角三角形及正方形45度角模型,我们可以从轴对称的视角构造出全等三角形,同样可以发现很多有意思的结论.
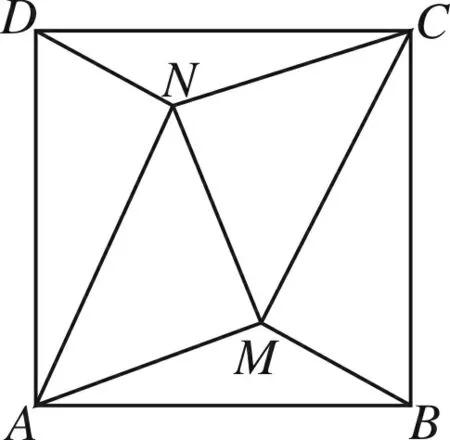
图8
例3 如图8,正方形ABCD中,∠MAN=∠MCN=45°,求证:(1)BM2+DN2=MN2;(2)S△MCN+S△MAB+S△NAD=S△MAN+S△MBC+S△NCD.
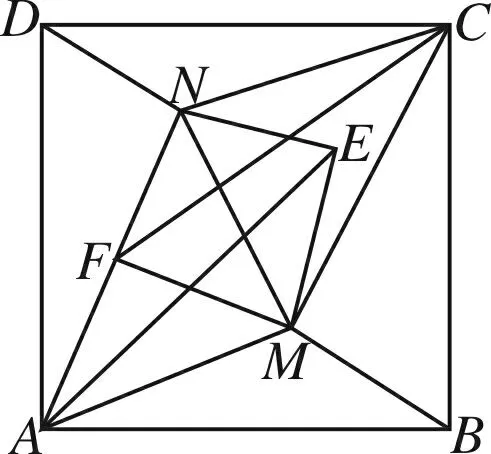
图9
证明(1)如图9,将△ABM沿AM翻折至△AEM,所以BM=EM,设∠BAM=∠EAM=x,可得∠DAN=∠EAN=45-x.同时AD=AE,AN=AN根据SAS可得△DAN≌△EAN,所以DN=NE.
将△BCM沿CM翻折至△FCM,所以BM=FM,同理可得△DCN≌△FCN,所以DN=FN,
由上得EM=FM,EN=FN,由SSS可得△MEN≌△MFN,因为∠MEN+∠MFN=180°,所以∠MEN=∠MFN=90°,根据勾股定理ME2+NE2=MN2,可得BM2+DN2=MN2.
(2)如图9,S△MCN+S△MAB+S△NAD=S△MCN+S△AME+S△ANE=S四边形AMCN+S△MEN,同理我们可以得到S△MAN+S△MBC+S△NCD=S四边形AMCN+S△MFN,所以S△MCN+S△MAB+S△NAD=S△MAN+S△MBC+S△NCD.
4 拓展3
前面我们主要从几何变换的角度来探究等腰直角三角形及正方形45度角模型,下面我们换个角度,用相似的眼光,来进一步探究此模型会给我们带来哪些结论.
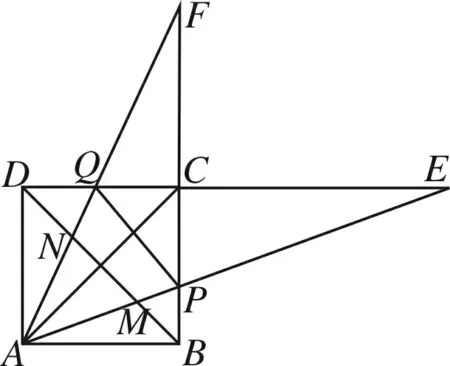
图10
例4 如图10,正方形ABCD中,∠PAQ=45°,延长AP交CD的延长线于E,延长AQ交BC的延长线于F,求证:
(1)AC2=CE·CF;
(2)AB2+BP2=PC·PF,AD2+DQ2=CQ·QE.
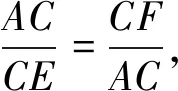
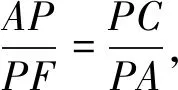
通过上述探究分析过程,我们可以发现,等腰直角三角形及正方形45度角模型中,蕴含着丰富而巧妙的几何关系,本文中所涉及的可以说只是冰山一角,关于此类模型的图形宝库中肯定还有很多有意思的结论值得挖掘.
