设计“惊异型”课堂提问 彰显数学神奇魅力

浙江衢州市教育局教研室 (邮编：324002)

浙江省衢州一中 李 盛 (邮编：324000)

理想的数学学习，是让学生忘记自己在学习，进入一种忘我的投入状态中，在无意识或潜意识中记忆、领会或“再创造”大量的数学知识.这样就要求我们在课堂教学中，要让数学知识和数学的思想方法，“进入学生骨子，流入学生心田”，让学生全身心投入数学学习之中，这样才能达到学习的高境界，并一辈子都难忘记.

提出具有震撼力的令人惊异型的数学问题，适当地对数学问题进行夸大，设置悬念，是吸引学生课堂注意力，让学生尽快进入理想数学学习的一条重要途径.通过惊异型数学问题的教学，可以化神奇为平凡，化复杂为简单，化抽象为直观，加深学生对数学的理解，让学生充分体会到数学的美妙,激发学生的创造性思维火花，提升数学核心素养.

1 惊异型数学问题的概念

查阅百度在线词典，惊异的意思是：感到意外，奇怪;惊奇诧异.令人惊异的数学问题,就是先将疑问悬在那儿，让学生念念不忘，存有种种猜想，在蓄积了一段时间后，再解开“悬念”，给出结果.目的是通过设置悬念，在问题的某一部分设置一个疑问或矛盾冲突，以造成学生某种急切期待和热烈关心的心理，吸引学生的注意力.

惊异型数学问题深刻反映了数学是深奥的,变化莫测又让人捉摸不透特点，就是突破常规，在兼顾教育和教学功能的同时，更为注重数学问题的独特风格，以及富有创造力的表达方式与手法，使数学问题具有“爆炸性”，具有瞬间动人心魄的震撼力和独特的魅力.设计优秀的惊异型数学问题，给学生带来的不仅是听觉和视觉冲击．而是心灵的震撼，可以提高学生对数学课的兴趣，改变学生对数学课枯燥无味的刻板印象.

2 惊异型数学问题的设计原则

要让课堂数学问题具有惊异性，关键是要提高数学问题的震撼力，让提问变成“高层次”的提问，确实能震动学生的心灵.其中最重要的一环，是惊异型数学问题的创作设计，需遵循如下创作原则.

2.1 科学性原则

设计惊异型数学问题，无论是文字表述的形式还是问题创意，都必须是科学的，不会出现歧义.

2.2 新颖性原则

提问的新颖性，能导致创造性理解.惊异型数学问题的设计一定要新颖, 要与时俱进地保持对社会、事物等高度的关注与前瞻性的思考，充分发挥想象力，采用各种创作手段，用一种与众不同的视角，将自己的教学观念表达和教学风格淋漓尽致地施展于问题创作中，道出自己的个性思考.让数学问题以更具个性化、更具创新意识的表达方式和更具创新的表现手法，迈向科学性、艺术性、实验性等更为广泛的探索之路.

2.3 “震撼”性原则

创意是数学问题的灵魂.所以“惊异型”数学问题的设计，要突出创意“惊异”的震撼作用：让它对于学生来说，应该有一定的内涵，耐人寻味，有时惊奇诧异有时疑，最后如同醍醐灌顶，直指人心.它不是潺潺溪水细细流淌，也不是和风细雨润物无声．而是暴风骤雨电闪雷鸣.精彩与深刻，尢如豁然打开了一扇智者进出的头脑风暴“旋转门”，在一瞬间让学生豁然开朗，有所顿悟，正是惊异型问题的优点所在.

2.4 主题性原则

“惊异型”数学问题的设计必须切主题，与教学内容紧密相联，能够对数学课堂教学有一定的暗示或提示作用.要以精炼性的文字,螺丝壳里做道场，要简洁，完整，有力，深刻，丰富，强有力地表达出问题的特殊心理效应，隐含令人震撼深思的主题，给学生带来强烈的心灵撼动，这是惊异型数学问题的永久魅力所在.

2.5 简练性原则

一个好的构思得来不易，“惊异型”数学问题的设计要简短而精练，方便地传达设计者的创作意图.

简，要简得明白，练要体现干练. 尽量追求一种含蓄、凝练的意境，突出本质，把丰富的含义和多样化的形式统一在一个简约的整体结构中，用最少的字将令人拍案叫绝的构思给学生最明确的意义和问题指向，言简意赅，达到了简约和含蓄的完美结合.

由于很多学生对文采非常敏感而且也很看重，“惊异型”数学问题有一定的文采，短小精悍，读起来自然会赏心悦目，无疑会一下子唤出学生心中那份珍藏的美感，让学生领悟到比短短几句话更多的内容.

总之，“惊异型”数学问题的设计，要题不惊人思不休，经过许许多多次的反复雕琢,精益求精，才能成为精髓.

3 惊异型数学问题的作用

“问题是数学的心脏”,数学问题在数学教学中占有不可忽视的重要位置.许多著名数学问题，我们总是津津乐道、如数家珍.它们会在潜移默化中充实我们的心灵、深刻影响我们的数学审美情趣，甚至理性思维方式和行为方式.

我们曾以“你的课中所提数学问题，震撼过学生的心灵吗？”为题，对数学教师进行访谈式调查，结果给我们的是顶级震撼，很多数学教师认为：数学问题一般不可能震撼学生心灵.但一滴水，在一些人看来，也许是微不足道的.然而，当它在极其干旱的环境中，与一些“极其渺小”的生命个体联系起来产生的效应却能直叩人们的心灵，其产生的力量也会重重地撞击人的心扉.一个好的数学问题，犹如炒菜中的味精，能起到决定性的惊异震撼作用.下面我们用实例来加以说明：

3.1 让学生感受数学的神奇魅力

有惊异型数学问题的课会很精彩!不是刻意炒作，也不要怀疑课堂中学生的激动是否理智，只要弄明白这个惊异型数学问题有着怎样的独特之处，让学生怀揣着急切和疑惑走向数学问题的发现，心中的疑惑也就有了答案.

案例1(“向量方法在立体几何中的应用”第一课时引入，李世杰课堂教学实录):

(1)师:写出与向量a={1，2，3}平行的一个向量.

生:{2，4，6}

(2)师:再写出与向量a={1，2，3}平行的一个向量.

生:{3，6，9}

(3)师:你一分钟内能写出一千个与a平行的向量吗？

一千个平行向量，这似乎是一个宏大的数学问题，也是充满神秘感且独具魅力的一个数学问题，让学生深感惊异.课堂内飘逸的空气中透着静谧和谐，因为这个问题带给学生的震撼实在太多了，学生惟一不变的动作是张大着嘴，那种场景令人叹为观止.

生1:只有一分钟,写不出来.一个个地写,时间来不及.

生2:不可能.

师:你现在不能做到的事情,想一想用数学的方法能不能做到，再想一想.

生3:ta.

师:对.应用参数的方法可以写出一千个与a平行的向量.但怎么表示呢?书面表达非常重要.

引导学生总结出两种表示方法:

答案12a,3a,…,1001a.

答案2ta,t=3,4,…1002,t∈N.(为本节课中直线的向量方程作伏笔)

师小结生活中遇到解决不了的问题,就想一想用数学的方法能不能解决.如上面问题的解决,充分体现了数学的简洁性和应用的广泛性.

注上述数学问题是从学生意想不到的角度提出的，在课堂上学生往往认为这是根本不可能做到的.课堂教学实践表明: 通过这一惊异型数学问题的解决,让学生切实感受到数学的神奇魅力，提高学生对数学课的兴趣，并切身体验数学知识应用的广泛性.

3.2 加深学生对数学的理解

惊异型课堂提问，可以深化学生对数学知识本质的理解,沟通知识之间的相互联系,在知识获得的同时,加深情感体验，培养数学能力.

案例2(李盛课堂教学简录) 写出一万个对数函数.

师分析题目要求写出的是对数函数，根据定义，一定具有y=logax这种形式，而对数函数里的x、y是不变的，因此，要写出一万个对数函数，只要给出一万个不同的a值就行了.问题是：怎样表述这一万个对数函数？

引导学生总结出两种表述策略：

方法1(列举式)y=log2x,y=log3x,y=log4x,…,y=log10001x.

方法2(体现函数思想)y=logax,a=2,3,4,…,10001,a∈N.

上面廖廖数笔，就写出了一万个对数函数，学生感到十分新奇，震撼，并产生共鸣.显然，方法2更能体现数学的简洁性，由于让a动了起来，可以让学生很好地体验对数函数细微的深刻内涵，既培养了学生的函数感，又加深了学生对对数函数的理解.

这在课堂中是一分钟的惊异！充分显示了数学问题的震撼力，这种简约之下的数学震撼，也是数学的艺术魅力所在！

也许有学生会提出：y=logax,a=1,2,3,4,…,10000,a∈N.这里可提示学生思考：有没有问题？学生们容易发现a=1不符合规定，可加深学生对对数底数不能为1的理解.

注案例1和案例2中的数学问题，让学生领略到了什么是惊异性数学问题,往往也是大气的数学问题(主要是指数量大、规模大、场面大、含量大而视觉冲击力强、心理震撼力大的数学问题)，它给学生视觉、心理的冲击、震撼非常大，并给学生留有悬念和无限的想象空间，能在短短的几秒钟内抓住学生的心，让学生产生欲罢不能、先睹为快的强烈冲动，吸引学生急着去了解事情的真相.

因此，从某种意义上讲，这种惊异型的数学问题，是一种不可多得的“抓心”艺术，能有效触动学生的心灵，让灵动的智慧和人文的光辉溢满课堂，使课堂教学高潮迭起，容易激发学生的兴奋点，带给学生一种全新的体验，为学生创造广阔的想象空间，经历一次美好的精神旅行，自然提升了数学问题的教学价值和审美价值.

3.3 培养学生数学化的观念

在一定程度上，数学问题是我们认识世界、把握世界和改造世界的一种方式.对实际问题的背景进行数学化处理，可以让学生用数学的观念认识世界，用数学的语言描述世界，通过数学化解决，可以充分发挥数学对生活的指导作用，化神奇为平凡，用数学的方法改造世界，产生“变不可能为可能”的奇迹，是发展和培养学生应用意识和应用能力的关键.

案例3一个小和尚,早晨上山,到山顶后在寺内寄宿一夜,第二天早晨仍按照原路下山,和尚的速度不一定,在路上可以走走、停停、跑跑，请问和尚上山和下山时经过的时间相同的点的个数是( )

A.0个 B.1个

C.2018个 D.A、B、C都有可能

分析初看这个问题与数学无关.实际上是数学中的存在性问题，利用交轨模型可以获得解决.

把一个和尚上山下山问题，改为等价的一个和尚上山，另一个和尚下山的轨迹相交问题，这样“和尚上山和下山时经过的时间相同的点的个数”，等于两个和尚分别上山和下山时的相遇点个数.

(1)第一层次答案:由于路程与时间的关系， 0个.如：第一天小和尚6点上山，用了1个半小时到山上,第二天小和尚8点下山，用了1个小时，9点到山下.这样和尚上山和下山时经过的时间相同的点就不存在；

(2)第二层次答案:刚好相遇，和尚上山和下山时经过的时间相同的点为1个；

(3)第三层次答案:如果和尚是个调皮的小和尚，来回跑动，相遇交点就可以为任意个(有限个).

知识的作用在于应用.从本例可见,神奇的数学知识，可以应用在人生的每个方面，亦可以应用在生活的每个细节上.掌握数学知识的迁移与应用规律，实现学以致用,可以提高数学的综合能力.

3.4 改进学生的学习方式

案例4(李盛课堂教学实录)你一分钟能解一万道数学题吗？

课堂中提出该问题的时候，多数学生都认为：这是不可能的.但教学的效果是惊人的.经过反复引导，学生们给出了如下几个答案：

答案1一万个数学计算题

0×a=,a=1,2,…,10000.

万题同答案：0.

答案2一万个方程组

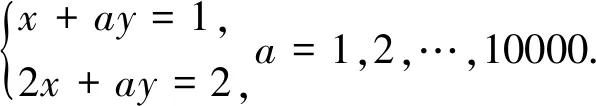
万题同一解：

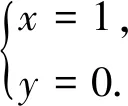
答案3一万个周期函数

求函数f(x)=cosax(a=1,2,…,10000)的最小正周期.

实际上，这只是一般化的数学结论具有的一万个特例,是学生们平常都会做都会求的数学常识，只是没有从这样的视角去分析挖掘而已.

追问1你一分钟能解的一万个数学题，会是什么样的数学问题？

引导学生总结出：具有共性的批量数学问题.

批量解题，打开了数学创造之门，这是数学创造的奇迹.

追问2如果你一分钟能解一万个数学题，用的是什么数学思想方法？

引导学生提炼出：对字母参数进行功能开发，将一般性结论中的字母参数“动态化”，是函数思想的创造性应用.

当然，这是开放性问题，答案不惟一.

注一个惊异型数学问题，具有磅礴大气，课堂上再配上整齐排列的重磅大字，会强烈地刺激着学生的兴奋点.从视觉效果上看，有一种恢弘的气势，让学生产生一种“大江东去”的豪迈和“飞流直下三千尺”的痛快淋漓，可以有效改变学生的思考方式，经常把数学知识与生活实际联系起来，加深知识内涵的理解，同时也改进了学生的学习方式，让学生切实意识到数学是有用的，数学处处有神奇.

4 惊异型数学问题的创作来源

4.1 改造常规课堂提问

案例5在“两角差的余弦公式”教学中，教材引入设计的是测电视塔高度问题.开课后精心设计悬念式诗意导言：“我们能不能，不上山测得山高，不过河测得河宽，不爬上电视塔测得塔高，这是什么神秘武器？学习了本节课的内容后，你就会知道结果了”.这句导言激发了学生极大的探索热情.

注教学中不以纤巧华美的词藻取胜，而是以平易通俗、准确有力、能为所有学生接受的语言征服学生，取得令人拍案叫绝的结果.

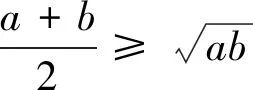
①

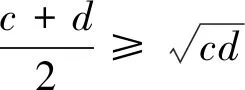
通常把上式写成a>0,b>0,c>0,d>0时，

②

提出问题 对于二个正数，有不等式①成立；对于四个正数， 有不等式②成立，我们自然会猜测:对于三个正数，也存在类似的不等式，即

③

想一想能否直接由不等式①推出不等式③？不等式①也是不等式③的特殊情形吗？

试一试类似于上面做法，应用不等式②推证8个正数的类似不等式(通常称为算术——几何平均值不等式)，并通过特殊化得到5个，6个，7个正数的类似不等式(通常称为算术——几何平均值不等式)，它的一般情形也是成立的.

评注通过加一加，不仅获得了新的不等式，还让学生学到了创新的一般技法：加一加，乘一乘，变一变，想一想，试一试.问题设计巧夺天工，结果出人意料，由四元，八元基本不等式来反推出小于四元，八元的基本不等式，结论还可推到一般形式，学生会震撼问题奇特而耐人寻味.这种反向论证的新方法，既让学生体验了n元平均不等式证明的历史脉络，又学到了数学创新的方法.

4.2 精心预设, 光芒四射

经过精心预设，我们可以将一些普通数学问题改造成让学生惊异的数学问题.如：

案例7(李世杰课堂教学实录)在函数模型教学中, 讲授折纸中的学问.

师:数学真神奇，现代高科技本质上是数学技术.古希腊物理学家阿基米德说过:“给我一个支点,我能撬动地球.”这句话运用了夸张和比喻等修辞方法，作为一名教师,总希望能找到这样一个四两拨千斤的支点,撑起整个课堂,最大限度的点燃学生的主体性.我们数学中能不能想到类似说法.

生:沉思,默想.

师:给我一张纸，送你上月球.

生1:不可能.

生2，生3，生4众说纷纭:我给你一张纸,你送我上月球.

师:如果怎么简单,就能把你送上月球,那还要航天部门干什么?显然,这是一个虚拟的数学问题,下面我们进行数学化剖析.

(出示问题) 一张厚度为0.1毫米的薄纸，不断对折，折51次后，纸叠得有多厚？

想象一下，你手里有一张足够大的白纸.现在，你的任务是，把它折叠51次.那么，它有多高？

一个冰箱？一层楼？或者一栋摩天大厦那么高？不是，差太多了，这个厚度超过了地球和太阳之间的距离.

师生一起探讨, 发现:不断对折，折51次后，纸叠得有多厚？

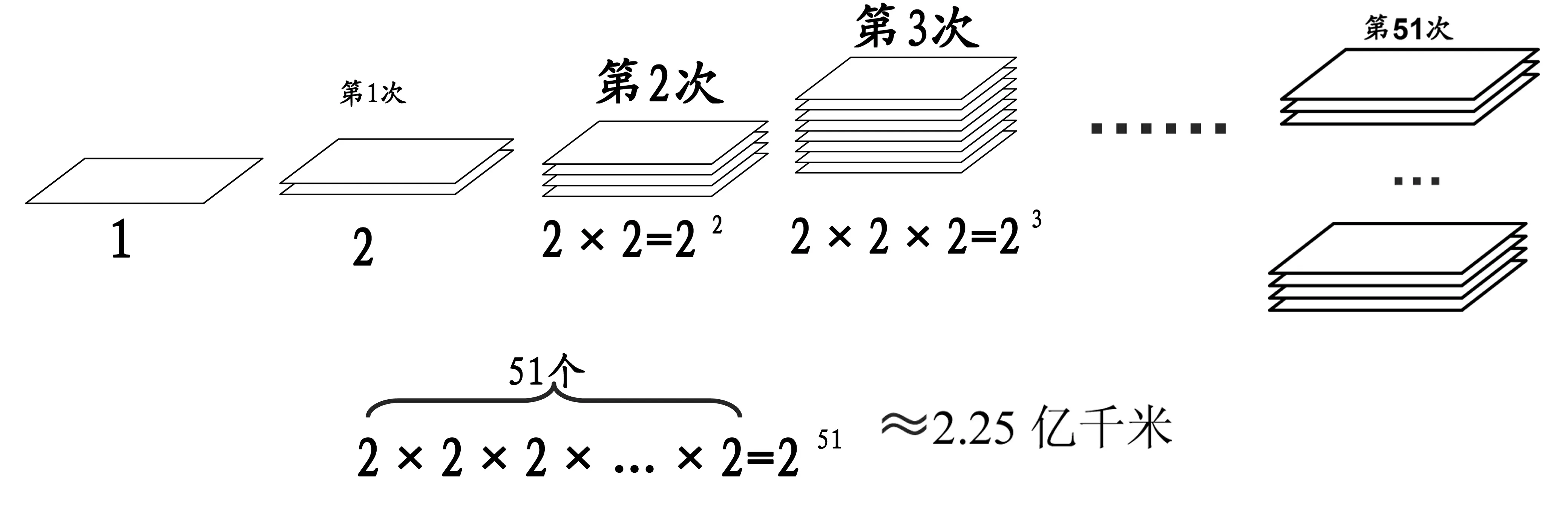
图1

现在要把这一张纸对折51次,其厚度的计算就应该为0.1毫米的2的51次方倍，计算后的答案是：2.25亿千米！2.25亿千米是什么概念？

地球的赤道长度是40075.24千米，2.25亿千米就相当于绕赤道56189.3圈！太阳与地球之间的距离是1.5亿千米左右(在远日点，距离是1.5亿公里；在近日点，距离在1.47亿公里以内)，2.25亿千米相当于太阳与地球之间的距离的1.5倍！

一般地，对折x次后,厚度的增长规律满足函数模型y=0.1×2x.

注数学与生活的联系是这么密切，这个问题蕴含着深刻的数学道理，潜藏着神奇的数学奥秘.高中学生虽已读了十几年数学知识了，但可能都是纸上谈兵，只会做题和考试，而建模是去解决实际问题.从书中到书外，从理论到实践，这是一次飞跃.每张纸对折一次，厚度就翻一倍.而随着厚度的增加，折了七八次后，折叠起来的纸张就会很厚了，而可供折叠的纸面积就越小，再想继续对折就不可能了 (参见文献3) .这类案例在数学中数不胜数，而此问题绝对是一枝奇葩.处处绽放着数学智慧的幽默之花，充满了浓郁的人文关怀气息，别有另一番风味，让学生感悟生命、享受震撼，惊异到无语.使学生经历了无与伦比的情感历程.相信即使到老，这批学生也不会忘却这一个动人的数学问题.

4.3 抓住课堂现场的细微契机生成

教学不是完全根据教师的事先预设按部就班地进行.在课堂中发现和关注可以开发的课堂细节，反映教师的睿智和思想；捕捉和利用细节，则体现教师的实力和功力. 只有师生的思维在碰撞中产生了“火花”，课堂教学才能不断生成.

案例8(李盛课堂教学实录)在上函数定义域用区间表示时，初次引入无穷大“∞”符号，有学生嘀咕：无穷大是什么东西？

师：(灵机一动追问)无穷大与我们的生活有关吗？

很多学生的回答是：无关.太大了.

师：真的无关吗？

生：沉思

师：实际上，无穷大与我们的生活密切相关.如我们任意走过一步，就包括“无穷”多个位置.只是由于习惯成自然，没有这样去思考联想罢了.

注这是让学生惊异的一个数学问题，它具有简约精悍的独特风格和扣人心弦的震撼魅力.拉近了学生生活与“无穷大”概念的距离，加深了学生对所学知识的理解.

4.4 开发体现数学知识与思想方法应用价值的提问

案例9《体外震波碎石机》的工作原理见示意图，它是如何将碎石的能量输入人体内的？

如图2，在焦点A位置固定一个火花塞，在某一瞬间通入几万伏的高压电，发生电火花，电火花的能量足够将处于第二焦点的坚硬如钢结石打碎.

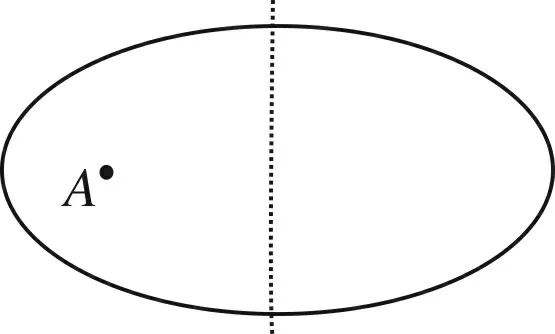
图2

知识背景电火花的能量经半椭球反射杯进行聚焦，能量传送到第二焦点.如果结石刚好位于该处，则被此能量击碎.

评注问题尽管不大，但能很好体现焦点的应用价值，留给学生无限感叹.

4.5 依托数学创新理论进行设计

一个数学新概念的出现，往往能带来一个全新数学领域的诞生.

案例10 函数与方程是重要的数学模型，它们以“解集”的方式刻画自然形态.不等式也有解集，我们能用不等式的解集来表述大自然千姿百态的美丽吗？

答案是肯定的.借助高级软件和编程，我们得到了令人惊异的结果，举二个实例：

图4

图3

(1)不等式[1+(x+y)4][1+(y-x)4][1+(3-2y)4]≤82的解集图案(如图3)，形似金元宝，我们把此不等式称为金元宝不等式；

(2)不等式sinx+siny+cos(x+y)≥1+4sinxsinycos(x+y)的解集图案(如图4).

图5

整个图案是由“环环相扣”的基本图案(如图5)通过上下左右周期性平移组成. 我们把此不等式称为环环相扣不等式.

评注一个个枯燥的不等式演变成一张张精美生动的几何图形，精美绝伦,美伦美奂, 这是“数学之美”的新发现,在文献[2-8]中也作过研究.这些惊异型数学问题的教学，不仅从形式上触及学生的视觉网膜，而且有“视觉冲击力”和“情感震撼力” ，其创意穿过学生头脑，触及学生的心灵. 有助于增强课堂教学的感染力和效果，寓教于乐，大大激发了学生学习的热情，学生不仅用聆听，还用心去体会享受.

5 惊异型数学问题的教学实效及有待继续研究的问题

惊异型数学问题的教学，不仅从形式上触及学生的视觉网膜，而且有“视觉冲击力”和“情感震撼力” ，其创意穿过学生头脑，触及学生的心灵, 增强课堂教学的感染力和效果，将会开辟出一个数学教育新天地.寓教于乐，大大激发了学生学习的热情，学生不仅用聆听，还用心去体会享受.高中数学课堂教学实践证明：有意识用一些恰当的惊异型数学问题引导教学，能够很好地体现数学的神奇魅力，只要适时恰当使用，能提高课堂教学的艺术性，有效提高课堂教学效率.用问题惊异性震撼课堂，学生能更深刻感受数学思想方法的精妙绝伦.有待研究的问题有以下三个.

5.1 要紧紧围绕教学内容进行设计

一个好的惊异型数学问题，源于对教材内容准确、深刻地解读，和宽阔、深厚的数学文化构建，要紧紧围绕教学内容进行设计，关键是如何和内容有机结合，使之水乳交融，浑然一体，要按照美的规律来创造，作为美的信息载体，成为人类文化情感和美质的积淀. 且比常规教法更适合学生，这样可以充分发挥师生双方的积极性.

惊异型问题并不一定适用于所有的课堂教学，问题设计不当会导致不好的后果.所以对惊异型问题所具有的极强的感染力和渗透力，应该综合认识和运用.

5.2 内容选用要精美

课堂教学是一门艺术，课堂教学中惊异型数学问题的成功运用同样也是一门艺术.数学是一座智慧的城堡，在这神秘的世界里有许多惊异型数学趣题，教学中选用的内容一定要精美,要有教学魅力，体现在可吸引学生的注意力继续学习，有审美价值，有长久深远的感染力、穿透力与亲和力.

但一个惊异型数学问题的集聚，有些像一个镜子的碎片重新收录在一起，从不同向度看，映出的镜像都会不同，这就要求我们在选用时要作深层次的思考.

5.3 使用时机要恰当

惊异型数学问题使用的时机要恰当，是在上课之初，还是在快下课时，是在讲授前，还是在讲授中或讲授后，都要根据教学内容和授课实际精心安排.

6 结语

本文提出了“惊异型”数学问题的概念，讨论了惊异型数学问题的设计原则，揭示了惊异型数学问题在教学中的作用，总结了惊异型数学问题的创作来源，最后提出几个有待继续研究的相关问题.

教学实践证明：创设有效的惊异型数学问题，能够很好地体现数学的神奇魅力，适时恰当使用,能有效提高课堂教学效率.我们的研究仅仅是冰山一角，希望能起到抛砖引玉的作用.乐于见到有更多更好的超级惊异型数学问题的出现，以提高数学的震撼力，用那精巧的情节和简练中透出的深度，在课堂中一下子就能击中学生的内心，撼动学生的心灵，让他们体会到：数学这么有用，数学真神奇！相信惊异型数学问题的生命力会很强，在数学园地会占据一席之地，焕发着勃勃生机,不但能够承载思想，传播真理，而且能够改变人的思维方式，震撼心灵.