创造性挖掘试题 针对性提升素养——关于一道高考模拟解析几何题的评讲

广东省东莞市麻涌中学 (邮编：523000)

1 引言

目前，教学一线的高三复习课仍然以老套路“教师选取奇、巧、新、特等题目+教师包办例题解答，不暴露解题思维+学生机械模仿重复训练+教师总结解题技巧”的教学模式为主，这样不但禁锢了学生的思维，对培养学生数学核心素养鲜有作用，而且加重了学生的负担，影响学习积极性和自信心[1].2019年佛山高三一模理科数学解析几何题是对2018年全国I卷理科数学第19题改编而来，是培养学生数学核心素养的绝佳载体.该试题的讲评以问题为核心，探究为主线，学生自主探究与合作探究相结合，充分调动各方面的积极因素参与课堂教学，培养学生核心素养.

2 试题评讲

2.1 试题背景分析—落实数据分析

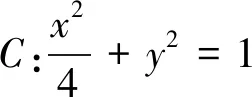
(1)若x1=0，求△OAB的面积；

(2)在x轴上是否存在定点T，使直线TA、TB与y轴围成的三角形始终为等腰三角形.

本题考查椭圆的标准方程及简单性质，直线与椭圆的位置关系，三角形面积，直线关于x轴对称等，考查学生的推理论证能力、运算求解能力，考查数形结合，化归转化思想，考查的核心素养是逻辑推理、直观想象、数学运算、数据分析.试题的重点是题设几何条件的代数转化，难点是选择恰当的化归方式优化运算.第(1)问满分5分，班级平均为4.2分，第(2)问满分7分，班级平均为1.6分.因此本题着重讲评第(2)问.

问题1同学们要善于观察，认真审题，你从这道题中获取了哪些信息？解题的突破口在哪里？

学生独立思考处理信息，小组同伴相互交流，教师巡堂、观察，适时点拨.

设计意图数学解答题，尤其是压轴题有大量的数据，信息量很多，并且数据间联系盘根错节，教师必须引导学生通过数形结合，合理猜想，严谨推理，对获取的信息进行有效辨析、重组，才能形成解题思路的雏形.学生能否高效正确地解答试题，取决于学生分析试题时是否将数据分析的数学素养落实到位.本题的核心结论是“TA、TB与y轴围成的三角形始终为等腰三角形”，明显可见题目的问法“隐藏”了多种信息，譬如∠OTA与∠OTB互补，TA与TB的倾斜角互补，kTA+kTB=0等，若能高效对题目设问的辨识，转化，重组为kTA+kTB=0，自然而然就有许多可供选择的解题路径.而如何优化解题将是数学运算的主题了.

2.2 试题解法选取—优化数学运算

下面通过投影第一小组学生1的解答来点评.

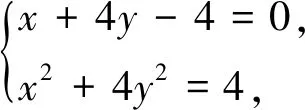
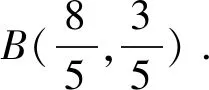
(2)由题知，直线l的斜率k存在，且k≠0，设直线l方程为y=kx-4k.联立

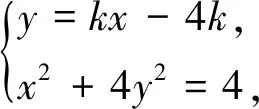
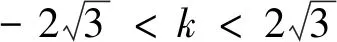
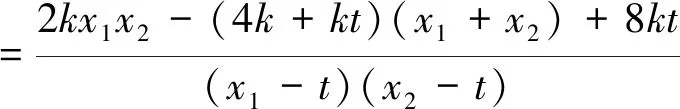
故在x轴上存在定点T(1,0)，使得直线TA、TB与y轴围成的三角形始终为等腰三角形.

师：哇，第一小组的解答太完美了，简直就是标准答案，太棒啦，让我们一起为第一小组喝彩！

此时班级响起了雷鸣般的掌声……

师：其他小组还有更好的方法吗？

即刻第二小组的学生2站在来分享小组的成果.

生1：我们小组的解答第(2)问的方法本质与第一小组的是一样的，只是我们根据以往过x轴上定点(t,0)的直线设法为x=my+t来优化运算.

学生2投影第二小组的解答过程.

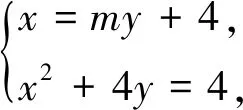
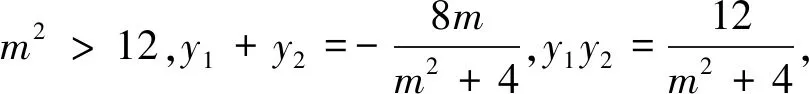
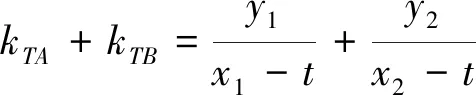
要使直线TA、TB与y轴围成的三角形始终为等腰三角形，则kTA+kTB=0，

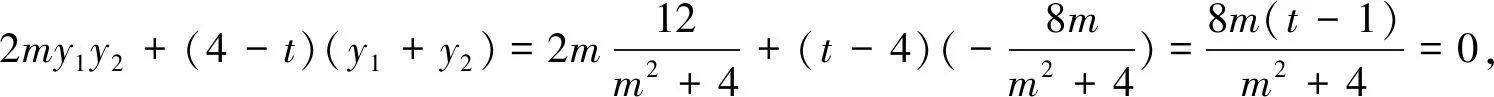
故在x轴上存在定点T(1,0)，使得直线TA、TB与y轴围成的三角形始终为等腰三角形.

师：你们都很棒，都做得很漂亮，老师佩服你们，为你们感到骄傲！这两个小组所用的方法都是破解此类解析几何题的通性通法：一是“图形”引路，一般需画出大致图形，把已知条件翻译到图形中，利用直线方程的点斜式，即可迅速表示出直线方程；二是“转化”桥梁，即会把求的“在x轴上是否存在定点T，使得直线TA、TB与y轴围成的三角形始终为等腰三角形”，根据图形特征，转化为斜率之间的关系，再把直线与椭圆的方程联立，利用根与系数关系，以及斜率公式即可求出定点.但在代数运算中，第二小组设的直线方程使得计算简化了好多！

设计意图数学运算是对试题中的数据分析，形成正确的解题思路后，选择最优化的运算方法，求得运算结果.在代数运算中需要选择恰当的代数形式，即需考虑直线的方程式对于优化运算的价值.本题中方程形式1：y=k(x-4)(k≠0)，方程形式2：x=my+4，将直线l的方程代入椭圆C的方程，利用韦达定理解答，比较上述两种方程形式，第二种韦达定理表达要简洁许多，同时目标式也很简洁，因而运算过程也简洁许多.从而促进学生数学运算核心素养的发展.

2.3 试题的来源—巧借数学抽象

试题2(2018年全国I卷理科数学第19题)设椭圆

的右焦点F，过F的直线l与C交于A、B两点，点M的坐标为(2,0).

(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明: ∠OMA=∠OMB.

问题2请同学们思考试题2，并比较试题1与试题2有什么联系与区别？解题思想方法类似吗？联系高考题，比较两题的异同，能让我们更好地把握命题规律.

设计意图试题1、试题2虽呈现的方式不同，但考查的核心知识点是一致的，仍然考查直线与圆锥曲线有两个交点的位置关系，都是“方程”与“直线倾斜角互补”问题，试题1是把试题2穿上了一层是否存在型的外衣，另外两题直线过的定点不同.在强调高考改革的今天，通过改编、创新等手段赋予高考典型试题新的生命，这成为高考命题的一种新走向，因此在高考备考中，要注意对高考真题考查核心知识和思想方法进行深度挖掘，把握其本质，掌握其规律，规范其步骤，做到“胸中有高考真题”，那么就能做到以不变应万变.让学生解答试题2并深度比较两题的异同，激发学生的探究乐趣，为进一步深挖试题的本质，培养学生的直观想象、逻辑推理、数学抽象、数学运算等核心素养做好铺垫.

教师巡堂，适时对各小组点拨引导，几分钟后，第三小组学生3举手分享小组合作探究成果.

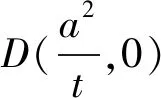
师：哇，第三小组同学太棒了，你的想法太富有想象力了，极具创造性，让我们再次为他们喝彩！同学们在学习过程中就是要敢于猜想，善于猜想，这样才能有所发现，有所创造！但猜想仅仅是建立在直观想象与归纳的基础上的，只有严密地推逻辑推理才能获得最本质、最核心的结论.

此时，学生心中已燃起了探究的火花，于是教师抛出了问题3.

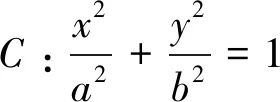
各小组根据解答试题1、2的通性通法开始紧张地小组合作探究，过了5分钟，第四小组通过严密的逻辑推理得出了结论1，并向全班同学投影证明过程并解释.

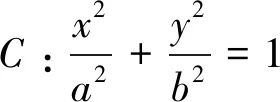
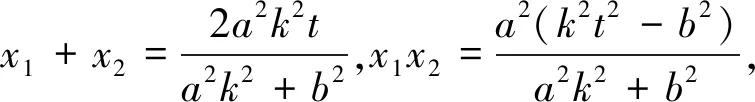
所以kAQ+kBQ=0，即∠OQA=∠OQB.

笔者大力表扬了第四小组的学生后，乘势而上，给出了问题4.

问题4结论1逆过来成立吗？请同学们继续思考、探究.

学生小组合作探究，教师巡视，也参与各小组的讨论，很快师生便共同得出了结论2并给出了证明.

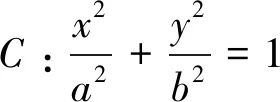
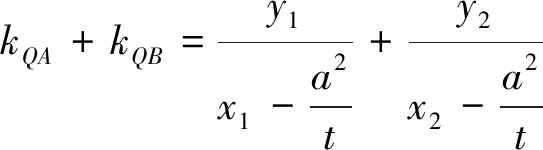
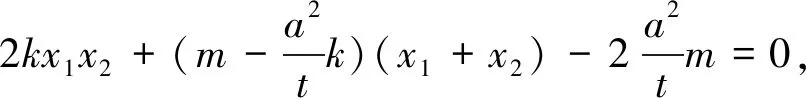
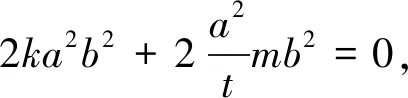
所以直线l恒过(t,0).

设计意图学生在问题2中比较试题1、2异同，教师鼓励学生根据椭圆的基本量与定点之间的关系合理猜想，培养了学生直观想象、数据处理的核心素养，然后给出了问题3、4，引导学生对一般点的探究，抽象出更一般的结论，目的是培养学生数学运算，数学抽象，逻辑推理等核心素养.

课堂进行到此时，试题1、2得到了一定程度的挖掘，但学生的探究激情已被点燃，意犹未尽，如果此时停止对试题本质的进一步挖掘，实属可惜，于是教师继续引导学生探究，给出了问题5.

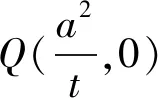
学生通过探究发现了结论3、4.

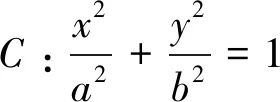
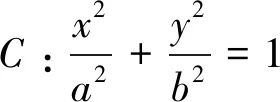
由椭圆类比到双曲线、抛物线，教师继续鼓励学生深度探究.

问题6根据我们已有的经验，椭圆、双曲线、抛物线的性质一般是统一优美的，刚才我们探究得出了椭圆的4个优美的一般性结论，在双曲线与抛物线中是否也存在呢？请同学继续展开探究.

学生小组合作探究，教师适时点拨，发现了如下结论.

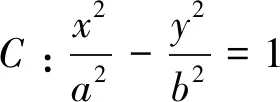
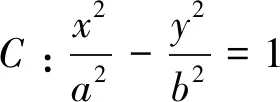
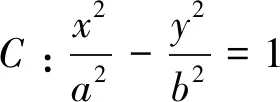
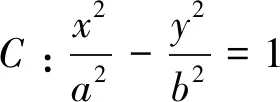
结论9抛物线C:y2=2px(其中p>0)，若点P(t,0)，点Q(-t,0)，过点P的直线l与抛物线相交于A、B，则 ∠OQA=∠OQB.

结论10抛物线C:y2=2px(其中p>0)，点Q(-t,0)，直线l与抛物线相交于A、B，且满足∠OQA与∠OQB相等,l不垂直于x轴，则直线l恒过定点(t,0).

结论11抛物线C:y2=2px(其中p>0)，若点P(t,0)，点Q(-t,0)，过点Q的直线与抛物线相交于A、B，则∠OPA与∠OPB互补.

结论12抛物线C:y2=2px(其中p>0)，点P(t,0)，直线l与抛物线相交于A、B，且满足∠OPA与∠OPB互补,l不垂直于x轴，则直线l恒过定点(-t,0).

设计意图经过师生共同探究得到椭圆的一般结论后，教师乘势鼓励学生类比探究双曲线、抛物线的一般结论.自然的想法，合理、恰当的知识迁移，学生们的探究精神在课堂上得到淋漓尽致的体现，培养了学生类比推理的能力，发展了学生逻辑推理、数学抽象、数学运算等核心素养.

此时课堂探究即将进入尾声，同学们沉浸在探究成功及发现数学美的喜悦中……教师鼓励学生课后继续探究，培养数学核心素养.

请大家选做课后习题中的其中一道：

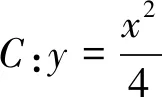
(1)当k=0时，分别求曲线C在点M和N处的切线方程；

(2)y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由.

2.(2013年陕西高考理科数学第20题)设抛物线C:y2=8x，若点B(-1,0)，设不垂直于x轴的直线l与C有两个不同交点P、Q，若x轴是∠PBQ的角平分线，证明l过定点(1,0)，反之也成立.

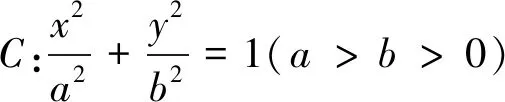
(1)求C的方程；

(2)x轴上是否存在点Q，使得k变化时，总有∠AQO=∠BQO，若存在请求出点Q的坐标，若不存在，请说明理由.

设计意图因材施教，弹性作业，巩固所学，培养学生数学核心素养.

3 评后感受

南京大学段康产教授说：“研究高考真题，典型模拟题，才能把握命题规律，它们就是最好的复习资料.”认真研究历年高考真题，典型模拟题，充分挖掘，不难找出命题轨迹，从而把握难度[2].教师在讲解高考真题或典型模拟题时不要一味地替学生读题，读完之后马上提问“该题是什么题型，用什么方法？”，这其实是造成学生不良解题习惯的根本原因.教师应当引导学生关注“本题所涉及的基本知识”，“每个条件得到什么结论？”，“求解的目标需要哪些条件？”，“本题与我们头脑里的哪些解题经验相关”，从而促进学生数据分析、逻辑推理等素养的发展.课堂上应给予学生充分的动脑、动手、动口的时间和空间，学生合作探究，教师巡视、观察，适时给予点拨，让学生上台交流解题思路，相互评价，然后教师点评，适时给予点晴之笔，追问“解决该类题目的通性通法是什么？”，“能否推广试题的一般结论”，引导学生深度挖掘试题隐藏的知识本质，不断地让学生把“触类旁通”，“举一反三”放在心上，实践于课堂，从而促进学生数学抽象、逻辑推理、数据分析、数学运算等数学素养的发展.也正如陕西师大罗增儒教授所说：要让学生通过有限的典型考题的学习去领悟无限道题的数学机智.数学解题重在一个悟字，从一个题拓展为一类题，举一反三才能触类旁通，通者方能渡过题海，登上胜利的彼岸[3].