“任意”还是“存在”
2019-04-18安徽省颍上第一中学邮编236200
安徽省颍上第一中学 (邮编:236200)
1 缘起
笔者所在学校最近进行了一次五校联考,理科第20题与文科第21题为同一题,其中第二问的参考答案引起了部分老师的质疑,并且在教研会上进行了激烈的探讨.试题及参考答案如下:
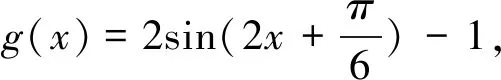
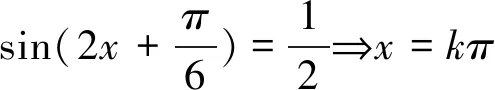
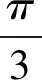
2 教研质疑与困惑
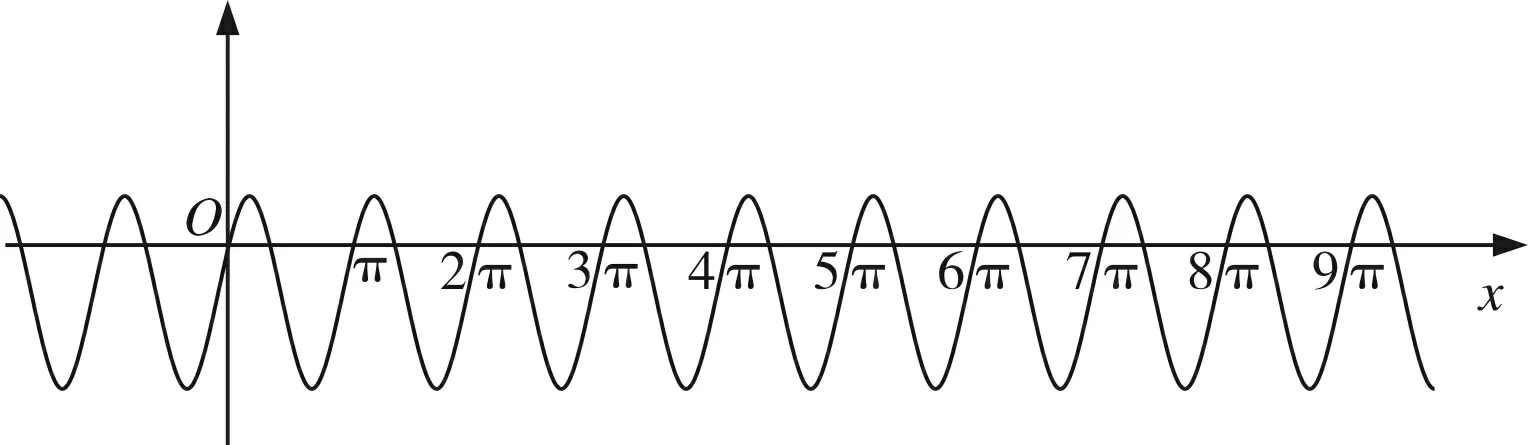
图1
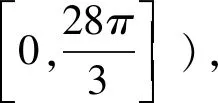
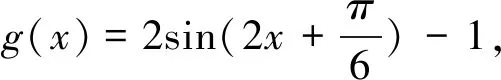
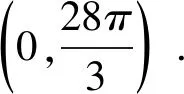
此时问题似乎聚焦到对区间[a,b]的理解上去了,那么问题1中的区间[a,b]前面被省略的量词到底是理解为“任意”还是“存在”呢?如果在问题1中重新还原被省略的量词,又该如何还原呢?大家在尝试给区间[a,b]添加量词的过程中发现,无论是添加量词“任意”还是“存在”,阅读起来都会非常拗口,而且也使得问题更加难以理解,教研一度陷入困境!
3 回归集合,再度质疑
事实上,求含参数问题的最值或取值范围时,通常不对参数附加量词,而是先将其固定为“常数”,再求它们的取值范围.笔者认为量词的添加困难主要来源于问题1中的“关系式”是从关系式所确定的“集合”中分离出来的[1],所以应该回归到集合关系.由此在教研会上提出将问题1等价转化为
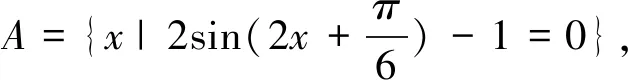
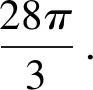
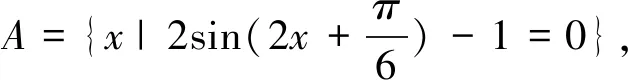
一石激起千层浪,笔者的提议很快遭到了其他老师的质疑,质疑的内容主要为两点:一是根据问题4,可以得出b-a的取值范围为(0,10π),这样就说明问题1与问题2并不是对立问题,与我们的认知相冲突;二是问题3与问题4都回避了对区间[a,b]添加量词的做法,虽然一般不对参数附加量词,但是并不代表不能附加量词.
4 深度教研,答疑解惑
为了探究问题的“真相”,笔者尝试用以下例题来加以说明.
例1设集合A={0},若(a,b)中含有A中的元素,求b-a的取值范围.
例2设集合A={0},若(a,b)中不含有A中的元素,求b-a的取值范围.
显然例1与例2中b-a的取值范围都是(0,+∞).从而写出以下两个真命题,即
命题1设a
命题2设a 由于“取值范围”具有充要性,因此命题1与命题2的否命题应该也是真命题.但是在不附加量词的情况下,容易对命题1与命题2的否命题产生误解,所以参考文献1的做法,可以分别改写成 命题3设a 命题4设a 显然,命题3的否命题是 命题5设a 而命题4与命题5并不是等价命题,所以例1与例2也就不是对立问题了.由此笔者对同仁们的质疑作出回应:首先问题1与问题2,即问题3与问题4并不是对立问题;其次问题3与问题4都可以对区间[a,b]添加量词“存在”,从而改写成 问题5与问题6表明问题1与问题2中的“至少存在”和“至多存在”是针对集合A而言的,而区间[a,b]都可以附加量词“存在”. 为什么很多教师,甚至资深老教师都会被问题1与问题2所困惑呢?笔者认为这是对区间[a,b]和数值b-a进行不等价转化而造成的,前者是集合,后者是该集合的测度,两者不可混为一谈.若设集合I={M|M⊆R},问题1中区间[a,b]∈D1,问题2中的区间[a,b]∈D2,那么D2是D1在I中的补集.但是所求问题是“b-a的取值范围”,即D1与D2中元素的测度的取值范围F1与F2,如果想当然地认为F2是F1在R中的补集,就会错误地认为问题1与问题2是对立问题.同样地,问题1可以简略地表述为:“若[a,b]∈D1,则b-a的取值范围是F1.”其中[a,b]∈D1是问题1中的条件,而不是所求问题的结论,否则就会造成理解上的困惑.所以笔者建议该类问题都应该回归到“集合”的角度去分析,这样可以有效消除问题中量词被省略后带来的理解误区.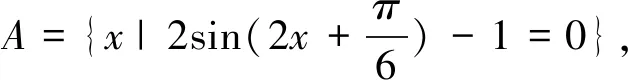
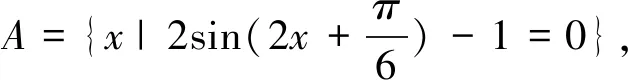
5 结束语
