核心素养下的初中数学课堂教学的实践与反思——以从算式到方程(第1课时)为例

安徽省巢湖市柘皋镇初级中学 (邮编：238062 )

在教育部近几年所颁布的《关于全面深化课程改革落实立德树人根本任务的意见》中，明确界定了核心素养，即学生应具备的适应终身发展和社会发展需要的必备品格和关键能力[1].纵观国内，发展学生核心素养逐渐成为基础教育界最令人瞩目的热点话题，因此，如何在初中数学课堂教学中培育学生的数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学核心素养就显得尤为关键.下面就以人教版初中数学教材七年级上册的3.1节的第1课时——从算式到方程的教学实践为例进行探讨：

1 教学实录

1.1 创设问题情境

问题1 一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶，客车的行驶速度是70km/h，卡车的行驶速度是60km/h，客车比卡车早1h经过B地，问A、B两地之间的距离是多少?

问题2 我国民间流传着许多趣味题，它们多以顺口溜的形式表述.请大家看这样一个数学问题：一群老头去赶集，半路买了一堆梨，一人一个多一个，一人两个少两梨，请问君子知道否，几个老头几个梨？

师：你会用算术方法解决这两个问题吗？

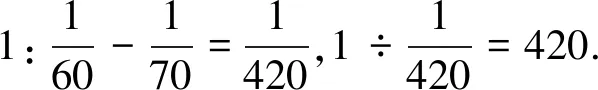
生2：2+1=3，2-1=1，3÷1=3，3×1+1=4.

师：问题中涉及哪些量，这些量之间有什么关系？

生3：问题1中的等量关系是客车比卡车早1h经过B地.

生4：问题2中的等量关系是两次分配过程中梨的总数量相等.

师：你认为应引进什么样的未知量？如何用式子表示问题中的相等关系？

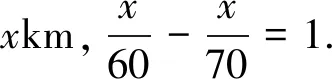
生6：设有x个老头，得：x+1=2x-2.

师：我们把列出的式子叫什么?你能归纳出它的定义吗？

生7：方程，含有未知数的等式叫方程.

师：对于上面的问题，你还能列出其他方程吗？如果能，你依据的是哪个相等关系？

生：……

设计意图首先设置两个问题情境以引导学生尝试列算式，并让他们用算术方法解决问题，然后逐步引导学生列出含未知数的式子，寻找存在的相等关系后列出方程，从而引出方程的概念，也在学生思考、交流和讨论的过程中，培养了学生的数学运算能力和数学抽象能力.学生通过思考发现问题1采用算术方法较容易解决，但却不适用于问题2，这样便产生了新旧知识上的矛盾冲突，使学生认识到了进一步学习的必要性，更引导了学生走进实际生活去感受数学的魅力.同时，通过学生之间的合作与交流，得出了问题的多种解答方法，培养了学生的创新意识以及数学抽象等数学核心素养.

1.2 设计探究活动

活动1 比较列算式和列方程解决问题各有什么特点？

师：试比较列算式和列方程解决应用题，你有什么感悟？

生8：列算式解题有多个步骤，列方程解决问题只有一步.

生9：用算术方法解题时，列出的算式用的是已知数；而用方程解决问题时，方程中既含有已知数，又含有用字母表示的未知数.

生10：算术方法解题思考方向是逆向的，方程解决问题思考方向是顺向的.

师：“从实际问题到方程”的步骤有哪些？关键是什么？

生11：(1)审——审题，找到已知量和未知量之间的相等关系；(2)设——设未知数；(3)列——根据相等关系列出方程.

生12：关键是准确找出数量之间的相等关系.

设计意图让学生通过对列算式与列方程解决问题作比较，分别归纳出它们的特点，从中感受到从算术方法到代数方法是数学的进步，有利于问题的解决，方程为我们解决问题带来方便.通过引导学生归纳列方程解决问题的步骤，培养了学生由实际问题抽象出数学模型的能力以及逻辑推理、数学建模等数学核心素养.

活动2 学习一元一次的方程的定义.

师：根据下列问题，设未知数并列出方程：

(1)用一根长24cm的铁丝围成一个正方形，正方形的边长是多少？

(2)一台计算机已使用1700h，预计每月再使用150h，经过多少月这台计算机的使用时间达到规定的检修时间2450h？

(3)某校女生占全体学生数的52%，比男生多80人,这个学校有多少学生[2]？

生13：设正方形的边长为xcm，列方程为 4x=24.

生14：设x月后这台计算机的使用时间达到2450h，那么在x月里这台计算机使用了150xh.列方程为1700+15x=2450.

生15：设这个学校的学生数为x,那么女生数为0.52x, 男生数为(1-0.52)x.列方程为0.52x-(1-0.52)x=80.

师：观察上面的例题，列出的三个方程有什么特征？

生16：只含有一个未知数x，未知数x的指数都是1，等号两边都是整式.

师：只含有一个未知数(元)，未知数的次数都是1，等号两边都是整式，这样的方程叫做一元一次方程.

设计意图通过探究例题，让学生熟练“寻找相等关系→设未知数→列出方程”的解题步骤，培养了学生的观察能力、归纳能力和分析问题、解决问题能力以及直观想象等数学核心素养.

1.3 巩固拓展训练

师：(1)下列式子哪些是方程，哪些是一元一次方程？

①x=1，②3x+2=x-7，③-a+3>0，

④-3x+1.8=3y，⑤x2+2x-6=0.

(2)根据下列问题，设未知数，列出方程，并指出是不是一元一次方程：

①环形跑道一周长400m，沿跑道跑多少周，可以跑3 000m？

②甲种铅笔每支0.3 元，乙种铅笔每支0.6元，用9元钱买了两种铅笔共20支，两种铅笔各买了多少支？

③一个梯形的下底比上底多2cm，高是5cm，面积是40cm2，求上底．

④用买10个大水杯的钱，可以买15 个小水杯，大水杯比小水杯的单价多5 元，两种水杯的单价各是多少元？

设计意图使学生对于方程与一元一次方程的概念的认识，以及列方程的基本步骤得到巩固，在教给学生数学知识的过程中，渗透了数学模型的思想方法，培养学生的思维品质和应用意识以及数学建模等数学核心素养.

2 教学反思

2.1 聚焦核心概念

概念教学是初中数学课堂教学中最重要的成分，而生成数学概念的过程是典型的数学抽象的过程.本节课的主要内容是方程及一元一次方程的概念，根据问题中的数量关系设未知数建立方程模型.在实际教学中，教师通过设计不同的问题情境，引导学生进行感知、抽象和归纳，概括出这类方程和一元一次方程的属性，有利于加深学生对于方程及一元一次方程概念的深层理解.教师有意识地按“寻找相等关系→设未知数→列出方程”的步骤组织学生进行探究，渗透数学核心素养，激发学生的学习兴趣，萌发学生的求知欲望，培养学生由实际问题抽象出数学模型的能力.

2.2 关注核心理念

《义务教育数学课程标准(2011年版)》指出：数学教学活动应激发学生兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维；另外，要注重培养学生良好的数学学习习惯，使学生掌握恰当的数学学习方法.本节课的教学难点是从列算式到列方程的思维习惯的转变.在小学，学生习惯于采用算术方法来解决问题，而对于如何设未知数，如何寻找等量关系，如何用含有字母的式子表示相等关系，虽然也有所接触，但明显不够熟悉，从算术方法过渡到代数方法的思维转变存在一定的困难.因此，本节课在实际教学时首先设置了两个问题情境，引导学生分别用列算式和列方程的方法来解决，让学生比较算术方法和方程方法的区别，使他们在解决问题的过程中体会到列方程解应用题的优越性，从而更加重视方程的学习，进而培养了学生的数学核心素养，更实现了他们的核心思维理念的转变.

2.3 培养核心素养

将实际问题中的数量关系用方程形式表示出来，就是建立一种数学模型，这种建模思想在本章中占主导地位.本节课紧紧围绕“数学核心素养”展开教学，教师出示问题串，让学生设未知数、列出方程，一方面是要分散列方程这一教学难点，化整为零地培养由实际问题抽象出方程模型的能力，另一方面是通过一些具体的方程归纳出一元一次方程的概念，培养学生的数学运算、数学抽象、数学建模等核心素养以及创新意识.学生在分组讨论、合作交流过程中，体验到方程是刻画现实世界的有效模型，初步感受到用方程解决实际问题较以前的方法更简单，并且还是一种通用的方法与手段，从而在感悟中使他们发现问题、分析问题和解决问题的能力得到升华，数学核心素养也得到全方位培养.

数学核心素养的培养是使学生得到全面发展的关键一步，作为一线数学老师，更要注重提升自身的数学素养，进一步学习数学核心素养的相关理论知识，转变教学理念，切实将培育学生核心素养融入到每一节课的教学环节中，从而实现学生的全面发展.