基于虚拟障碍物法的无震荡航路规划
2019-04-17陈天德黄炎焱沈炜
陈天德, 黄炎焱, 沈炜
(南京理工大学 自动化学院, 江苏 南京 210094)
0 引言
路径规划在移动机器人工程领域,如仿生机器人[1]、无人车[2]、无人机[3]、以及工业机械臂[4]等,是十分重要的研究内容。同时,在灾害、突发事故应急系统与军事辅助决策中也不乏有路径规划的身影[5-6]。目前,常用的路径规划方法有A*算法、人工势场法、神经网络法等[7]。人工势场法[8]作为路径规划的一种算法,其数学描述简洁、美观,在环境少知、甚至未知的情况下,可以实时求解航路点且所得航路较为平滑[9],在许多工程领域中的成功运用也证明该方法的有效性[10-12]。因此,在路径规划中,人工势场法举足轻重,受到了很大的重视。
然而由于算法本身的设计思想,局部极小值陷阱仍是传统人工势场法的严重缺点。目前,已有多种跳出局部极小值陷阱的方法,这些改进方法主要是从势函数模型本身入手,通过改变势函数模型来克服缺陷,如引入速度因素[13]、波动函数[14]、启发式搜索[15]、混沌算法[16]以及切换势函数法[17]等。这种改进思路类似于教室关门声音大,就对门进行改造来降低声音,虽然在一定程度上可以达到预期效果,但是对传统势函数模型进行了较大的改变,有的甚至已经失去了势函数法的基本思想以及算法简洁且易于实现的优势,改进后的算法需设定的参数较多且算法执行也较为复杂,而且对路径规划中存在的震荡问题并没有很好的解决。
震荡问题的出现会使得所解算出来的航路不够平滑,出现反复多次的“之”字路径[18],这严重影响了避碰效果和趋向目标的效率。震荡问题的出现主要是由于势函数法执行离散化所引起的,不是算法思想本身的问题。因此,从势函数本身出发,很难解决震荡问题。目前,针对航路点震荡问题,解决的方法还较少,现有方法多数都是通过参数设定来降低震荡程度,而并没有彻底解决震荡问题。
本文在不改变“门”的前提下,从“门”和“人”的关系入手,即人工势场法和路径规划任务的关系,对人工势场法存在的缺陷进行分析,相比已有的大部分文献,本文为保留人工势场法的优点,在不改变势函数模型的情况下,提出虚拟障碍物法和过滤震荡点法,在算法执行机制上克服人工势场法的缺陷。
1 传统人工势场法及其缺点
由于算法本身,人工势场法存在5个常见问题:1)由于局部极小值而存在陷阱区域;2)在相近障碍物之间不能识别路径;3)在障碍物前可能出现震荡;4)在狭窄通道中出现震荡;5)GNRON问题(障碍物在目标附近,目标不可及)。
出现问题1和问题3的根本原因是斥力势能非全局变量,可能会出现非目标点的零势能梯度点,即局部极小值点。由于势函数法编程实现时,一定会涉及到步长的确定,这就导致解算出的航路点不会正好为局部极小值点,而是在局部极小值点两侧来回震荡,即陷入局部极小值陷阱。当机器人、障碍物和目标点在一条直线上时,这种情形最有可能出现。也正是因为步长的存在,导致在机器人、障碍物和目标点不在一条直线上时,很可能在障碍物附近解算出的航路点是来回震荡前进的,这种震荡不是无休止的,当脱离障碍物影响范围时,也就摆脱了震荡状态。当然也可能由于步长设置与编译精度的原因,使得本应陷入局部极小值陷阱的航路点解算缓解为在障碍物前震荡多次后摆脱震荡的状态。如图1所示:障碍物影响距离ρ0为1 m,当步长l为0.2 m时,航路点解算陷入局部极小值陷阱;当步长l为0.1 m时,航路点解算在障碍物前震荡多次后摆脱震荡并到达了目标点。
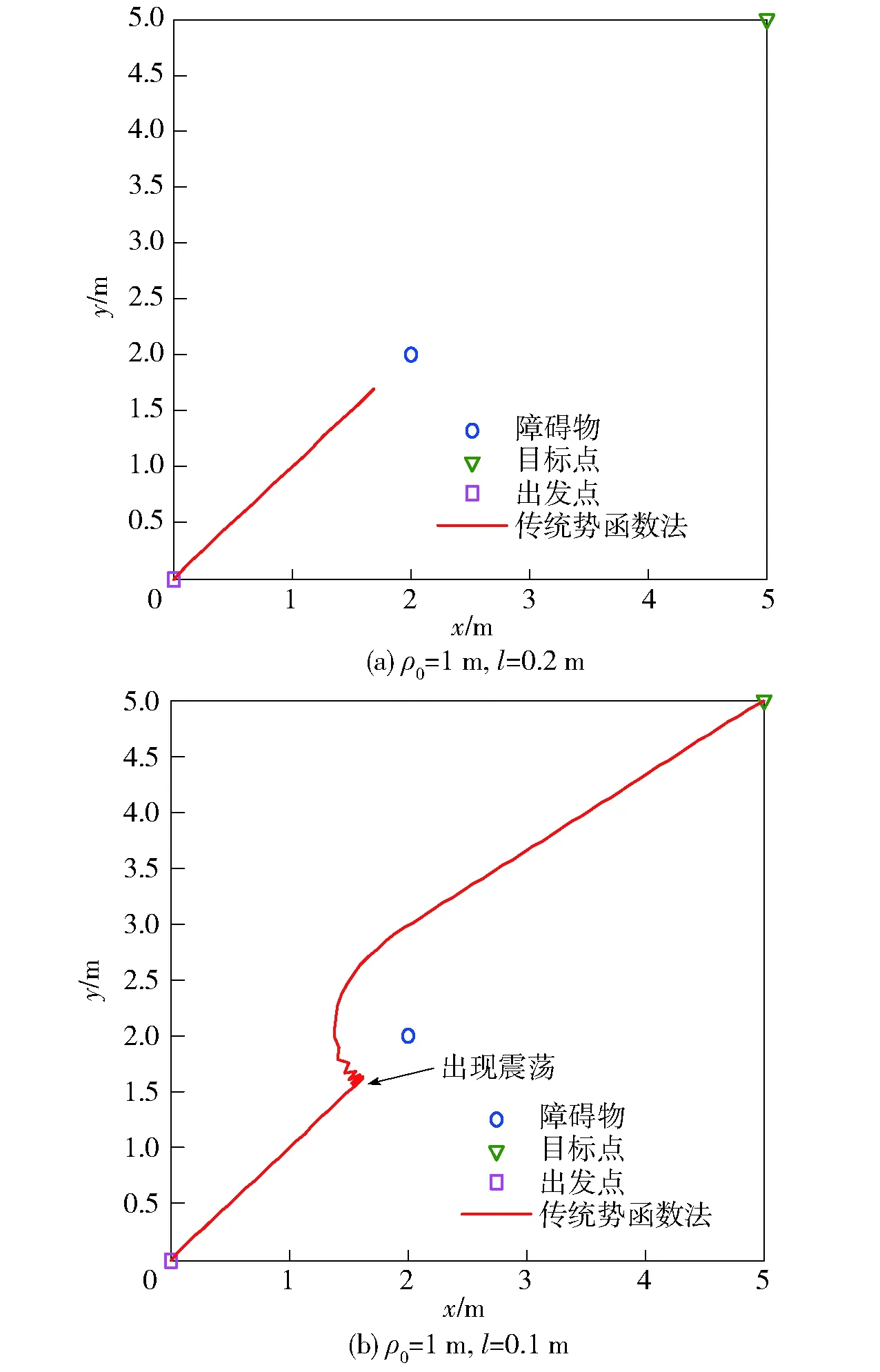
图1 步长设定的影响Fig.1 Simulated results of different step sizes
问题2相比其他问题,影响较小,主要是由于在斥力与引力的博弈中,斥力处于优势所引起的,只要势函数模型中步长、障碍物影响距离等相关参数设定得当,该问题能够避免。但是问题2没有处理好可能会升级为问题3甚至是问题1。
问题4的出现归根到底是由于算法执行的离散化,即步长设置所引起的。当然计算机精度也是离散化的标志,只是精度过高可以忽略离散的实质。因此问题4不是算法本身的问题,或者说不是算法思想的问题,仅为通过计算机语言实现算法时所引起的问题。换而言之,只要使用编程语言实现算法,该问题肯定会出现,只是严重程度不同而已。
因此以上问题可以归结为算法本身局部极小值以及算法执行所必须离散化所引起的。也就是说解决这些问题主要分为两步:第1步,在算法执行过程中,发现并解决局部极小值所引起的问题;第2步,在路径解算完后,遍历所有航路点,过滤掉因为算法执行离散化所引起的震荡航路点。
文献[19]提出虚拟障碍物的概念,当机器人陷入局部极小值陷阱时,引入虚拟障碍物,以此打破当前的力平衡状态,使得机器人摆脱局部极小值陷阱,该方法执行简单且有效。但文献[19]仅把虚拟障碍物放置在局部极小值点位置,这使得该方法在某些情况下不能高效地完成路径规划甚至有再次陷入局部极小值陷阱的危险,且也没有讨论如何求解局部极小值点,除此之外航路点震荡问题依旧没有被解决。
对于问题5,文献[20]通过在斥力势能函数中引入机器人与目标位置的距离,巧妙解决了GNRON问题,该模型被广泛应用。为了简化,假设机器人是一个质点且在二维空间内运动。机器人的位置坐标设为qr=(xR,yR)T,目标点的位置设置为qg,其引力势能函数为
(1)
式中:ξ为一个正比例系数;ρm(qr,qg)是机器人与目标点距离的m次方。斥力势能函数如下:

(2)
式中:η为一个正比例系数;ρ(qr,qo)为机器人到附近障碍物的最短距离,qo为在该障碍物上的一个点,机器人到该点的距离是机器人到该障碍物的最短距离。但该方法仅仅解决了GNRON问题,其他4个势函数固有问题仍然存在。
本文以该势函数模型为规划模型,在文献[19]所提出的虚拟障碍物概念基础上,所做的具体工作如下:1)提出陷入和逃出局部极小值陷阱的判断方法,增加虚拟障碍物放置位置的确定方法,以此形成改进型虚拟障碍物法,该算法自动识别航路点解算陷入或逃出局部极小值陷阱,综合考虑航路点解算陷入局部极小值陷阱时障碍物的当前态势并放置虚拟障碍物,以此来解决局部极小值陷阱问题,即问题1;2)对航路点震荡的原因进行分析,提出识别震荡航路点的方法,并针对航路点震荡的两种情形分别提出新航路点生成的具体方法,以此形成过滤震荡点法,对规划好的路径,该算法自动识别其震荡位置并过滤掉震荡航路点,以此消除震荡问题,即问题3和问题4.
2 虚拟障碍物法
2.1 虚拟障碍物法的原理
在一个未知环境中,使用势函数法来对移动机器人进行路径规划,当航路点解算陷入局部极小值陷阱时,由于局部极小值点是一个势场梯度为0的点,所以在该点移动机器人所受到的虚拟合外力为0,即机器人不能向任何方向移动。此时,在局部极小值点附近设置一个虚拟障碍物,它对机器人施加一个附加的斥力,以此打破当前的力平衡状态,使得陷入局部极小值陷阱的航路点解算摆脱局部极小值陷阱,从而继续进行接下来的航路点解算。
虚拟障碍物法嵌入到势函数法中后,势函数法的执行流程如图2所示。先判断当前航路点位置是否是目标点,如果是目标点,则结束路径规划,如果不是则判断当前航路点是否陷入局部极小值陷阱。如果没有陷入局部极小值陷阱,则直接进行下一个航路点的解算;如果陷入局部极小值陷阱,则放置虚拟障碍物,再进行下一个航路点的解算,并判断该航路点是否跳出局部极小值陷阱。若未跳出局部极小值陷阱,则继续放置虚拟障碍物;若跳出则撤除所放置的所有虚拟障碍物并进行下一个航路点的解算,以此循环执行下去。其中每次解算出的航路点都要先判断是否已到达目标位置,如果已到达目标位置,则进行震荡航路点的过滤并结束整个路径规划。
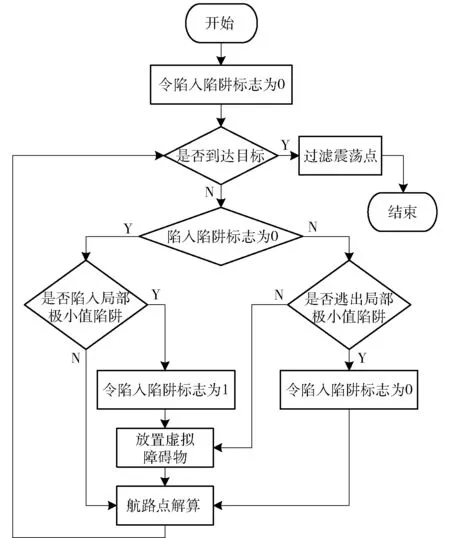
图2 引入虚拟障碍物法后的算法流程Fig.2 Flow chart of algorithm combined with the virtual obstacle method
2.2 虚拟障碍物法的步骤
2.2.1 判断是否陷入或逃出局部极小值陷阱
在静态二维空间中,由于航路点解算大体方向是指向目标位置的,即当前位置与目标点的连线方向,因此算法所得到的航路点应是不断靠近目标点的。而实际解算中偏离该方向的航路点则是由于障碍物的影响所造成的。这种影响可能会造成解算出的航路点远离目标点,而航路点解算陷入局部极小值陷阱同样也存在该现象。
目前航路点解算是否陷入局部极小值陷阱的判断方法已有一些,文献[19]给出的一个判断方法虽简单可行,但判断效率不高,会执行很多无谓的判断。本文在该方法的基础上进行了改进细化,提出一个判断算法执行是否陷入或逃出局部极小值陷阱的新方法。
当出现解算出的航路点开始远离目标位置时,则表明航路点解算可能陷入了局部极小值陷阱,此时执行更进一步的判断,否则当航路点持续靠近目标位置时,则不进行是否陷入局部极小值陷阱的判断,这样大大提高了判断的效率。由于算法执行的离散化,解算出的航路点不可能正好落在局部极小值点位置,而是在局部极小值点附近的区域内进行徘徊,因此判断是否陷入局部极小值陷阱的步骤如下:
步骤1解算第k步航路点的位置qk并计算该点与目标点的距离ρ(qk,qg)。
步骤2将计算得到的距离与上一步中航路点与目标点的距离进行比较,若ρ(qk,qg)<ρ(qk-1,qg),则令k=k+1并跳到步骤1,否则跳到步骤3.
步骤3继续解算航路点,得到第k+m步的航路点,m为算法执行的跨度值,m取20,计算第k+m步与第k步航路点之间的距离。若该距离ρ(qk+m,qk)≤d,d为一个较小的值,这里d取步长的5倍,则认为航路点解算陷入局部极小值陷阱,进行步骤4,否则令k=k+m+1并跳到步骤1.
步骤4根据当前态势,放置虚拟障碍物。
步骤5继续解算航路点,得到k+2m步航路点,计算该航路点与k+m步航路点距离以及这两个航路点与目标点的距离。若ρ(qk+2m,qk+m)>d且ρ(qk+2m,qg)<ρ(qk+m,qg),则认为航路点解算已跳出局部极小值陷阱,撤出虚拟障碍物,令k=k+2m+1并跳到步骤1,否则令k=k+m并继续进行步骤4.
步骤1到步骤3用来判断是否陷入局部极小值陷阱,步骤5用来判断是否逃出局部极小值陷阱,步骤4为放置虚拟障碍物。
2.2.2 放置虚拟障碍物
将机器人当作为一个圆,其圆心是机器人当前位置的坐标,记为qr,半径为机器人外形大小的一种体现,记为r. 虚拟障碍物放置在该圆上,即将虚拟障碍物对机器人施加的力看作机器人自身为摆脱局部极小值陷阱而采取的行动。
为了有效地使航路点解算跳出局部极小值陷阱,虚拟障碍物和当前航路点的连线应当与当前航路点和目标位置的连线相互垂直。如图3所示,虚拟障碍物位置1与位置2就是虚拟障碍物的备选位置。令机器人指向障碍物的向量为nR,O,机器人指向目标位置的向量为nR,G. 当航路点解算陷入局部极小值陷阱时,虚拟障碍物的放置需考虑实际障碍物的位置。需考虑的实际障碍物,其nR,O与nR,G的夹角为(0°,90°],根据方向不同将威胁区分成顺时针威胁区与逆时针威胁区。
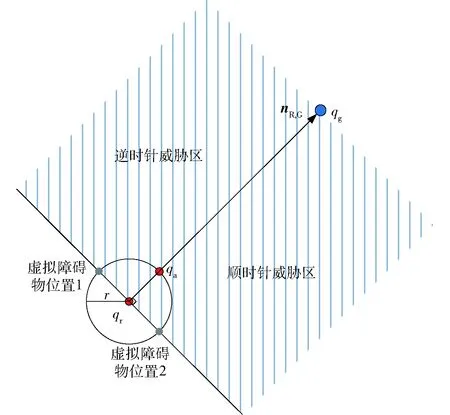
图3 机器人建模及威胁区确定示意图Fig.3 Schematic diagram of robot modeling and identification of threat zone
确定虚拟障碍物位置的具体过程如下:
步骤1判断是否陷入局部极小值陷阱,如果陷入,跳步骤2,否则结束放置。
步骤2筛选障碍物,分别计算逆时针威胁区与顺时针威胁区障碍物的个数nL、nR,以及两个威胁区中障碍物离机器人最近的距离dLmin、dRmin.
步骤3确定虚拟障碍物位置:1)nL>nR,虚拟障碍物放置在位置1;2)nL
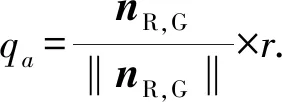
(3)
若虚拟障碍物放置在位置2,即顺时针90°位置,则
(4)
式中:方位角θ为90°.
3 过滤震荡航路点
通过势函数法解算出的路径由于算法执行离散化的影响不可避免地会出现一定程度的震荡。即使通过虚拟障碍物法使得陷入局部极小值陷阱的航路点解算摆脱了局部极小值陷阱,但大多数情况下,虚拟障碍物法仅能够将局部极小值陷阱问题减轻为在障碍物前出现有限次震荡问题。大部分震荡问题基本都是由于步长与障碍物影响距离设置不当所引起的,使得解算出的航路点一下子从障碍物影响距离以外进入影响距离以内,而后受到障碍物很大的斥力又一下子逃离障碍物的影响范围,就这样反复多次形成很大的震荡。为了算法能较好地执行,步长一定要远小于障碍物的影响距离,这样就可以降低大部分震荡的程度。若算法执行能够连续化,则斥力与引力充分博弈,所获得的航路点曲线将是非常平滑的。但由于算法程序化,离散是不可避免的,这也就导致震荡问题一定会出现,通过参数设置,可以减缓震荡的程度,但不能消除震荡。
为此,本文提出过滤震荡点法,不论震荡是由什么原因引起的,只要发生震荡,算法就会自动识别出震荡位置,并过滤震荡点。要过滤震荡航路点,首先要捕捉震荡的开始点qb与结束点qe. 设算法步长为l,k时刻的航路点位置为qk. 依次扫描所有航路点,当检测到k时刻的航路点与k-2时刻的航路点距离ρ(qk,qk-2)
当震荡的开始点与结束点位置确定后,则开始进行震荡点过滤。震荡点过滤分以下两种情况处理:

(5)

图4 异侧震荡示意图Fig.4 Schematic diagram of oscillation points on the different side
2)qe-qb为偶数,即qb与qe位于震荡的同侧,如图5所示,总体航路方向是朝向目标位置的,发生震荡即突变的点定是相对更靠近障碍物的。当ρ(qe,qb)

图5 同侧震荡示意图Fig.5 Schematic diagram of oscillation points on the same side
通过过滤震荡航路点,所获得的新航路长度为
stot=(总航路点数-1)×l+∑md+∑ms,
(6)
式中:总航路点包括起始点与目标点。
4 仿真结果与分析
假设机器人以恒定速度移动,虚拟力仅改变其运动方向。在一个10 m×10 m的开放空间中,有若干个圆形障碍物,机器人出发位置为(0 m, 0 m),目标点位置为(10 m, 10 m)。势函数中参数设定为:障碍物的影响距离ρ0为1 m,算法步长l为0.2 m,m=n=2,ξ=1,η=0.1.
当采用传统人工势场法时,如图6和图7所示,航路点解算陷入局部极小值陷阱,由于步长的存在即航路解算离散化,因此所解算出的航路点在局部极小值点附近来回震荡而无法到达目标位置。

图6 传统人工势场法的仿真结果Fig.6 Simulated result of path planning by traditional artificial potential field method
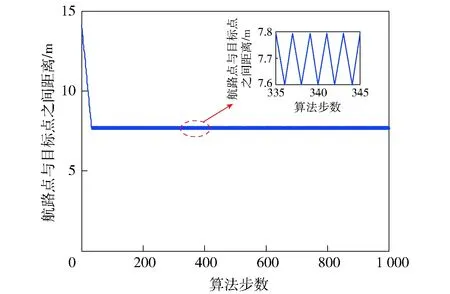
图7 传统势函数法执行过程中与目标点距离的变化Fig.7 Change of distance from the target point during the implementation of traditional potential function method
采用结合虚拟障碍物法的人工势场法进行航路规划,如图8和图9所示。算法自动识别出航路点解算已陷入局部极小值陷阱,再根据当前态势,确定虚拟障碍物的位置并放置虚拟障碍物。由于虚拟障碍物的出现,导致原本的力平衡状态被打破,航路点解算成功逃离局部极小值陷阱。但由于算法执行的离散化,虚拟障碍物法仅将局部极小值陷阱问题减轻为在障碍物前出现有限次震荡问题,此时该算法所得路径的长度为25.8 m.
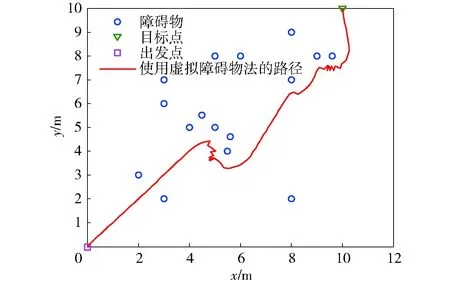
图8 结合虚拟障碍物法的势函数法仿真结果Fig.8 Simulated result of path planning by potential function method combined with virtual obstacle method

图9 使用虚拟障碍物法后与目标点距离的变化Fig.9 Change of distance from target point by virtual obstacle method
在使用虚拟障碍物法去解决局部极小值陷阱问题的同时,采用震荡点过滤的方法,如图10和图11所示,震荡点被成功消除,该算法解算出的路径长度为17.1 m.
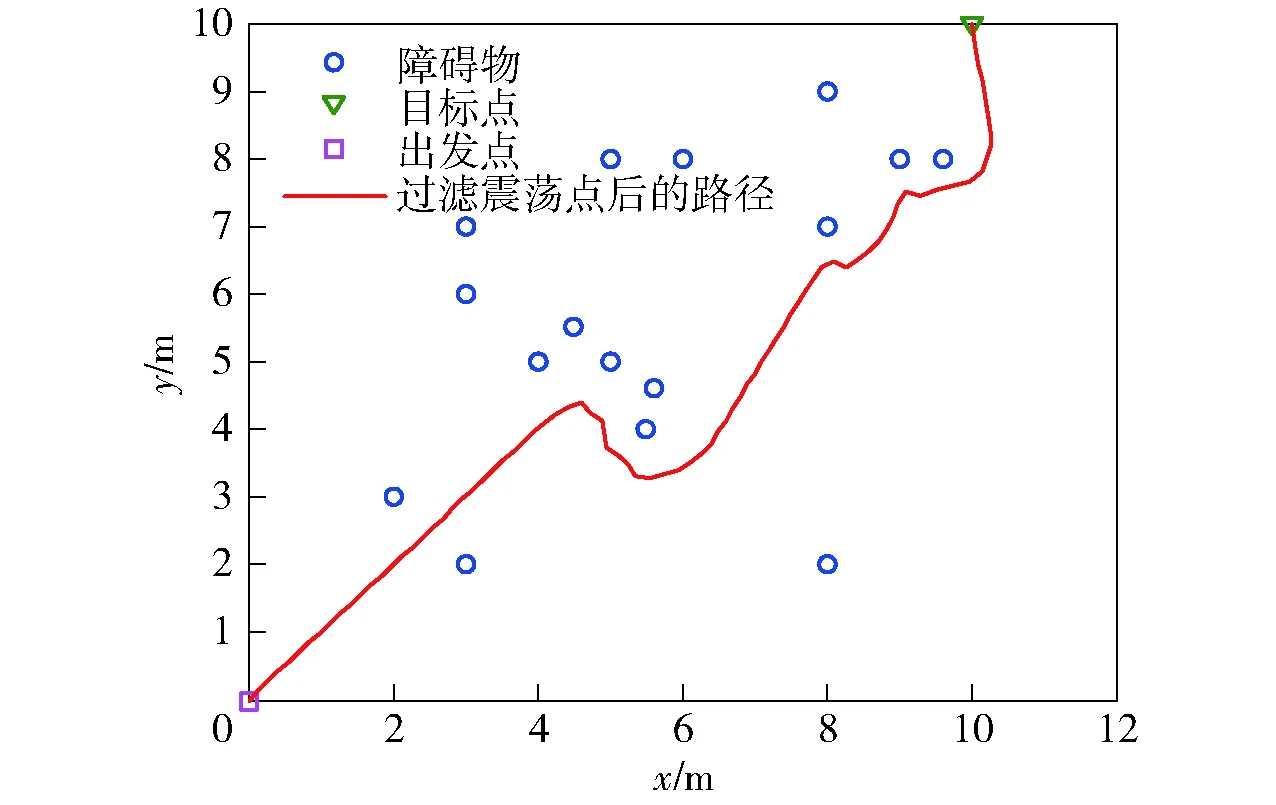
图10 过滤震荡点后的仿真结果Fig.10 Simulated result of path planning after filtering the oscillation points

图11 过滤震荡航路点后的与目标点距离变化Fig.11 Change of distance from target point after filtering the oscillation points
仿真结果表明,虚拟障碍物法能够有效地使陷入局部极小值陷阱的航路点解算成功逃脱陷阱并顺利到达目标位置,但是由于算法执行离散化,航路点震荡问题仍然不可避免,通过本文提出的过滤震荡点法,可以有效地消除震荡航路点,使规划的路径更为平滑。
5 结论
本文针对人工势场法存在的4个问题,对其进行原因分析,总结出导致这4个问题的根本原因是算法自身不可避免地存在局部极小值以及算法执行不可避免地离散化。针对两个根本原因,本文在不改变传统人工势场法的基础上:1)提出航路点解算陷入、逃出局部极小值陷阱的判断标准;2)引入虚拟障碍物概念,提出虚拟障碍物位置确定的标准;3)提出过滤震荡点法,对解算出的路径进行震荡点过滤,得到相对平滑的路径。在相同仿真环境下,对传统势函数法、引入虚拟障碍物的势函数法以及结合过滤震荡点的虚拟障碍物势函数法进行Matlab仿真。仿真结果证明,虚拟障碍物法和过滤震荡点法能够很好地解决局部极小值陷阱问题与航路点震荡问题。相比改变势函数模型来克服缺陷的改进方法,本文提出的方法在保留最纯粹势函数模型的基础上,仅从算法执行机制入手对人工势场法进行改进,保留了人工势场法数学描述简洁且易于执行的优势。
