考虑电枢与导轨实际接触状态的电磁轨道炮膛内磁场分析
2019-04-17殷强张合李豪杰杨宇鑫
殷强, 张合, 李豪杰, 杨宇鑫
(南京理工大学 智能弹药技术国防重点学科实验室, 江苏 南京 210094)
0 引言
电磁轨道炮(简称轨道炮)是一种能够将物体加速至超高速的新概念武器,它利用载流导体在磁场中受力的原理,驱动有效载荷,将电磁能转换为机械动能[1-2]。轨道炮主要应用前景包括远程精确打击、中近程防空反导、反临近空间目标等[3]。目前轨道炮主要发射动能弹,受身管寿命、热管理技术等方面的限制,发射率(单位时间内发射炮弹数量)不高,杀伤效能有限。为了实现精确打击并扩大杀伤效能,国内外已开始研究利用轨道炮发射含有引信的智能弹药或研制一体化制导弹药替换动能弹[4]。在膛内运动过程中,脉冲大电流在导轨和电枢内部流动,将在智能弹药部位产生强磁场,对其内部电子元器件产生电磁干扰,因此在设计轨道炮智能弹药时,需要对膛内磁场分布情况进行分析。
耿轶青等[5]和林庆华等[6]分析了电枢运动时产生的磁场特性,但其考察点位于导轨上方或轨道炮附近位置,并非智能弹药部位。殷强等[7-8]和李湘平等[9]分析了电枢静止状态和运动状态下智能弹药部位磁场分布情况,但他们分析的电枢并非实际发射的C型电枢,且没有考虑电枢与导轨(简称枢轨)实际接触状态。
目前,我国对于轨道炮的研究处于关键技术研究阶段,多采用中小口径轨道炮开展研究,然而由于电流量级、尺寸等参数的差异,研究成果能否外延到大口径轨道炮有待进一步研究。
本文从小口径轨道炮入手,采用实际发射使用的过盈C型电枢,分析其静止状态下枢轨接触压力分布特性,进而得到电枢内部电流分布情况,利用数值计算和有限元仿真的方法得到智能弹药部位各考察点的磁通密度值,结果与试验测量值基本吻合。在电枢运动状态下膛内磁场进行仿真和计算,得到各考察点磁通密度分布规律,在此基础上,采用模化方法,对大口径轨道炮膛内磁场分布特性进行了分析。结果表明,当满足一定相似关系时,能够实现不同口径轨道炮电枢速度和膛内磁场分布特性的近似匹配。研究结果能够为轨道炮智能弹药的电磁屏蔽设计提供参考。
1 计算模型和方法
1.1 计算模型
C型电枢轨道炮二维模型图如图1(a)所示,脉冲电流I由一侧导轨流入,流经电枢后,从另一侧导轨流出,脉冲电流在炮膛内产生强磁场B,与电枢电流作用,产生洛伦兹力F推动电枢运动。通过电枢与导轨的过盈配合来保证枢轨之间的良好接触,图1(a)中,虚线部分为初始装配时的电枢尾翼,Δ为电枢的过盈量,dt为电枢翼尖厚度,lt为电枢尾翼长度,r为电枢曲率半径,dh为电枢喉部厚度,d1为电枢前沿长度,s1为电枢前沿宽度,电枢前端为载荷,包含弹托和智能弹药,P点为智能弹药内部考察点位置,与电枢前沿的距离为d,w为导轨宽度。如图1(a)所示,电枢受到电磁力作用,向右侧炮口方向移动。考虑到智能弹药在膛内随电枢一起运动,二者之间相对静止,为了计算方便,假设电枢静止,导轨以速度v沿着-x轴方向移动,以电枢的曲率圆心为坐标原点,电枢长度方向为x轴,宽度方向为y轴,高度方向为z轴建立坐标系。从炮尾位置往炮口方向的轨道炮侧视图如图1(b)所示,s为导轨之间的间距,hr为导轨高度,ha为电枢高度,δ为导轨电流的趋肤深度。
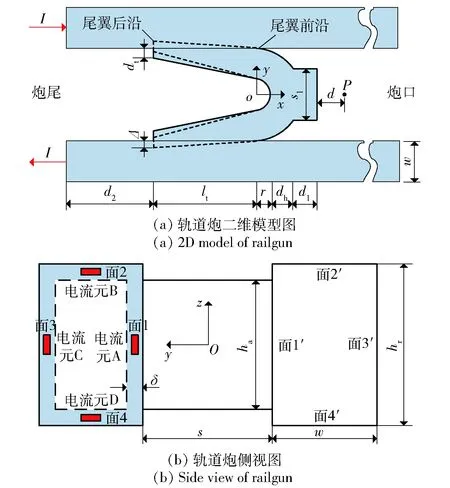
图1 轨道炮二维模型图及侧视图Fig.1 2D model and side view of railgun
1.2 计算方法
在本文计算中,忽略电枢起始运动时的边沿熔蚀和转捩等非线性作用,由于轨道炮发射系统加载的脉冲电流为低频电流,可以将轨道炮作为准静态系统进行研究[6],麦克斯韦方程的微分形式[10]为
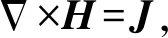
(1)
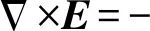
(2)

(3)
式中:H为磁场强度;J为电流密度;E为电场强度;B为磁通密度。
在图1(a)的轨道炮二维计算模型中,主要存在z轴方向磁通密度Bz,将(1)式~(3)式结合欧姆定律J=σ(E+vB),可以得到二维模型中导体的磁扩散方程为
(4)

(5)
利用毕奥- 萨伐尔定律可以求得考察点位置的磁通密度值为
(6)
式中:V为电流分布区域;r′为源点(电流元JdV)的矢径;r为场点矢径。
1.3 电磁轨道炮的模化研究方法
模化方法是指不直接研究自然现象或过程的本身,而是用与这些自然现象或过程相似的模型来进行研究的一种方法。对于轨道炮来说,目前尚未出现一种理想的模化方法可以同时实现两种不同口径轨道炮所有物理量的匹配[11]。由(4)式可以看出,速度是磁扩散方程的关键项,会影响导体内部电流密度分布,因此首先要满足速度的匹配。研究表明,在忽略摩擦力的理想情况下,当电流幅值的相似常数与几何相似常数相等(即电流线密度相等),它们同时还与时间相似常数相等时,可以实现匹配电枢速度的近似模化[12]。本文在考虑枢轨实际接触状态的条件下,首先分析不同口径轨道炮电枢速度的匹配,进而研究膛内磁场分布特性的匹配。
2 电枢静止状态下磁场分析
2.1 枢轨界面接触压力特性分析
采用30 mm×30 mm口径轨道炮进行分析,导轨间距s为30 mm,导轨宽度和高度分别为20 mm和40 mm,电枢各项参数如下:Δ为2 mm,dt为3 mm,lt为35 mm,r为5 mm,dh为7 mm,d1为13 mm,s1为16 mm;导轨材料为黄铜合金,电阻率为7.1×10-8Ω·m;电枢材料为Al-6061,电阻率为4.0×10-8Ω·m.
枢轨界面的接触压力主要由机械预紧力与电磁力组成[13]。图2为垂直于电枢尾翼的电磁力FEM,垂直于枢轨界面的电磁力分量为FNEM,将电枢尾翼近似为直线导体,A点为电流进入电枢位置点,采用文献[14]的方法,简单计算可以得到枢轨界面电磁力为
(7)
式中:lc为A点与电枢尾翼前沿的距离;L′为电感梯度,利用文献[1]中Kerrisk电感梯度计算公式可以得到L′为0.42 μH/m.
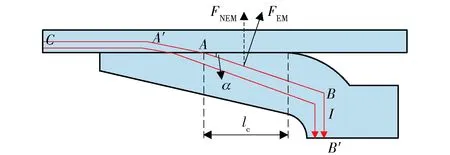
图2 垂直于电枢尾翼的电磁力示意图Fig.2 Schematic diagram of electromagnetic force perpendicular to armature trailing arm
使用有限元分析软件COMSOL Multiphysics分析过盈配合的枢轨接触,计算模型如图3所示。

图3 枢轨接触计算物理模型Fig.3 Calculation physical model for contact between armature and rail
将导轨视为刚体,电枢视为弹性变形体,杨氏模量为70 GPa,Poisson比为0.33,将电枢固定,导轨朝电枢总共移动过盈量2 mm的距离[14]。计算得到枢轨界面接触压强分布如图4所示。由图4中可以看出,装配后枢轨界面的接触压强具有极大的不均匀特性,最大接触压强为152 MPa. 位于尾翼中部边沿位置,提取尾翼边沿进行考察,得到边沿上各点的接触压强如图5中的接触压强1所示,图5中横坐标为各点与电枢尾翼后沿的距离,从中可以看出接触压强集中于7.5~27.0 mm位置,接触压强2为施加电磁力后尾翼边沿各点的接触压强。

图4 枢轨界面接触压强分布Fig.4 Contact pressure distribution on armature-rail interface

图5 电枢尾翼边沿接触压强和电流密度Fig.5 Contact pressure and current density along outer contact edge of armature trailing arm
2.2 电枢电流分布特性
输入脉冲电流如图6所示。由图6可知,电流在0.5 ms时间内上升到248 kA,随后逐渐下降,5 ms时电流为28 kA.

图6 输入电流曲线Fig.6 Input current curve
在图4基础上进一步施加电磁力,将峰值电流代入(7)式,计算得到枢轨界面的电磁力,将电磁力等效为压力载荷施加于尾翼内侧面[14],可以得到图5中的接触压强2. 从图5中可以看出:0~27 mm各点接触压强都有所增加,最大压强点保持不变,位于20 mm位置;27~35 mm各点压强始终为0,这些点与导轨不接触。
接触压力的大小直接影响着界面的接触电阻,从而影响枢轨界面的电流密度分布,Cooper-Mikic-Yovanovich (CMY)模型是一种适用最广的接触电阻模型,假设界面上的一系列微凸峰是随机分布的,凸峰高度符合高斯分布,接触表面粗糙度由粗糙平均高度和粗糙平均斜率表示[15]。将枢轨界面的接触压强代入COMSOL Multiphysics软件的CMY模型进行计算,得到枢轨界面的电流密度分布如图7所示。由图7可知,最大电流密度点位于尾翼边沿,其分布特性与接触压强分布类似。
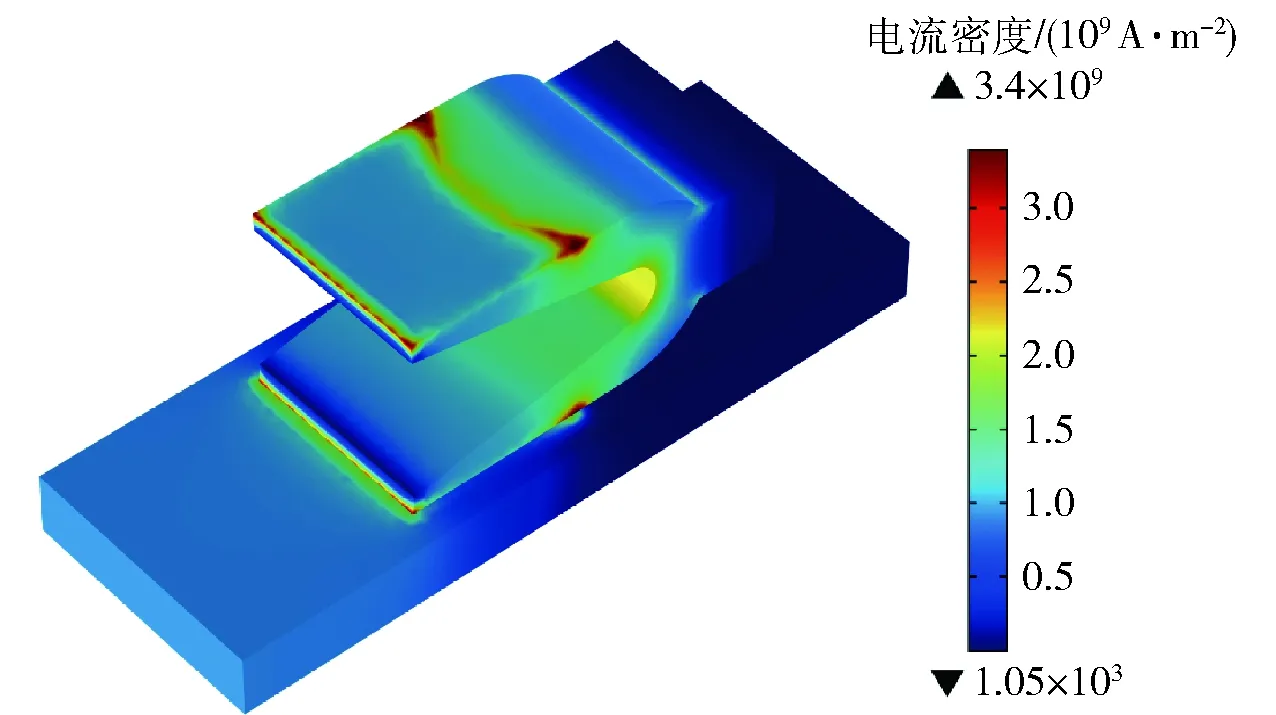
图7 枢轨界面电流密度分布Fig.7 Current density distribution on armature-rail interface
图5为尾翼边沿各点的电流密度值,最大电流密度点位于27 mm处,并非接触压强最大点的位置,这主要是由于接触压强大的区域接触电阻小,导致磁扩散速率低,并且电流主要沿着最短路径流动,因此造成枢轨接触面前沿部分电流密度大。电枢尾翼后沿也有较大的电流密度,这主要是由于导轨电阻率大于电枢电阻率。
2.3 膛内磁场数值计算与有限元仿真
参照图7中枢轨界面的电流密度分布,假设电枢内部电流为面电流分布,其中一半电枢的电流沿着图2中的电流面ABB′流动,对于斜线段AB来说(取z轴坐标为0),设A点坐标为(xA,yA),B点坐标为(xB,yB),可以求得其所在直线的方程为y=kx-kxA+yA,或者x=y/k-yA/k+xA,分别令其为f1(x)和f2(y),k为AB所在直线的斜率,k=(yB-yA)/(xB-xA), 斜线段AB电流元可以表示为Idl=Jsdxdzex+Jsdydzey, 其中Js为面电流密度,Js=I/ha. 设考察点坐标为(d, 0, 0), 简单分析可知,考察点主要存在z轴方向磁通密度,AB电流元的x轴方向分量产生的磁通密度为
(8)
式中:R为考察点至电流元的距离矢量。
产生的z轴方向磁通密度可以表示为
(9)
AB电流元的y轴方向分量在考察点产生的磁通密度Bz2为
(10)
直线段BB′产生的磁通密度为
(11)
将(9)式~(11)式相加,结果乘以2可以得到电枢电流在考察点产生的磁通密度。
电枢与导轨接触区域内部电流也采用斜线段面电流分布方式计算,如图2中的A′A,在考察点位置产生的磁通密度计算方法可参照前面所述。
导体电流趋肤深度计算公式[10]为
(12)
式中:f为电流频率。对于图6中的脉冲电流曲线,0.5 ms时计算可得频率f为200 Hz,将导轨和电枢材料的电导率代入(12)式计算可得趋肤深度分别为9.5 mm和7.1 mm.
如图1(b)所示,由于趋肤效应,导轨的4个面(面1~面4以及对应的面1′~面4′)都有电流分布,假设导轨各表面的电流分布为无厚度的面电流[16],位于导轨内部0.5δ深度。导轨电流的计算范围为炮尾到电枢尾翼后沿,长度为d2. 考虑电流的邻近效应,取导轨面1和面3(面1′和面3′)的电流分布系数比为4∶1,峰值电流时刻的δ=9.5 mm.
结合图7的枢轨界面电流密度以及计算得到的峰值时刻电枢趋肤深度,采用两种面电流坐标进行比较,分别为数值计算1:A′(-0.035 m,0.025 m)、A(-0.007 m,0.015 m)、B(0.012 m,0.006 m)、B′(0.012 m,0 m),数值计算2:将A点横坐标改为-21 mm,其他点的坐标保持不变。
利用COMSOL Multiphysics软件进行分析对比,按照导轨和电枢尺寸及材料建立仿真模型,导轨尾部到电枢尾翼后沿长度大于4倍口径,导轨和电枢接触长度为27 mm,以模拟实际枢轨接触界面,在导轨模型的两端直接导入图6所示的脉冲电流。
2.4 试验与结果分析
参照文献[7]的试验方法,将电枢固定,对电枢前端中轴线一系列点进行磁场测量试验,其横坐标为50~100 mm,测量得到各点的峰值磁通密度与数值计算和有限元仿真得到的结果进行对比,如图8所示。
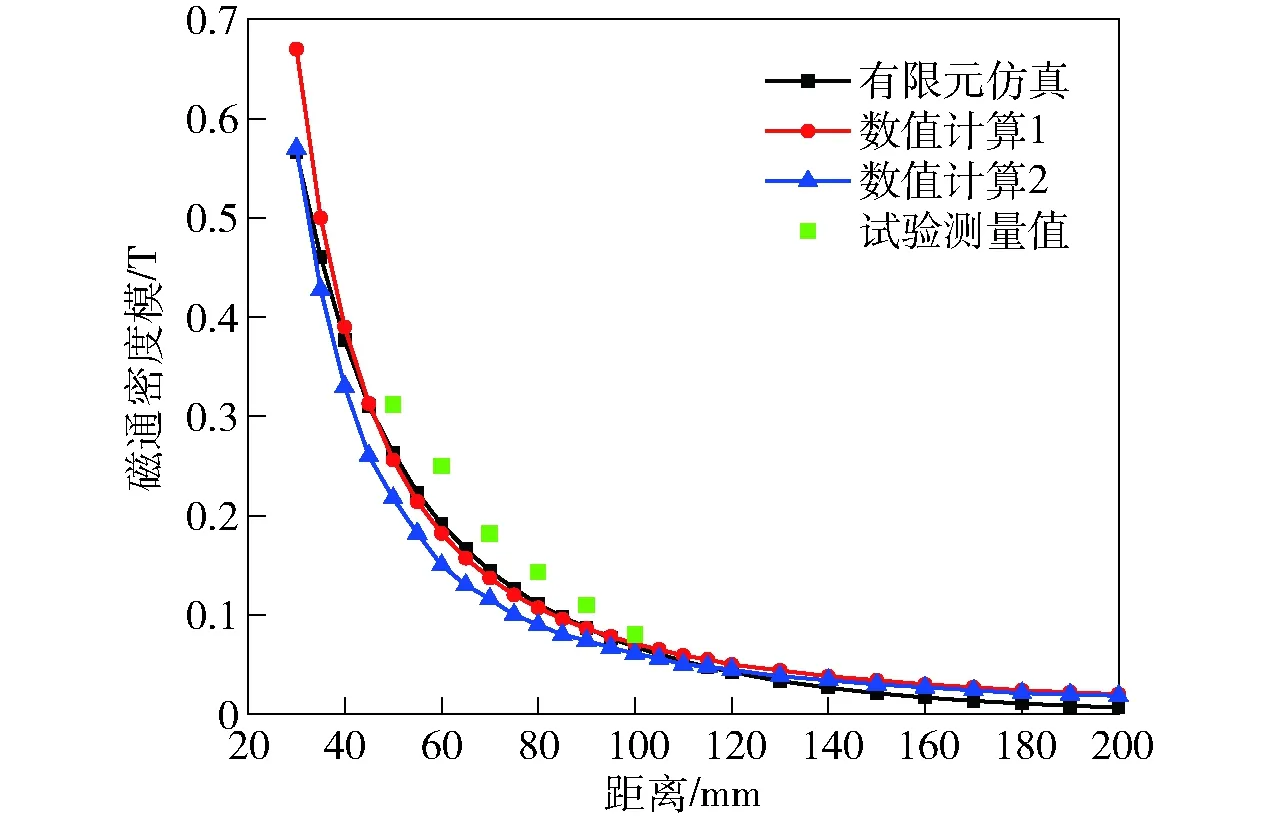
图8 各考察点峰值磁通密度模Fig.8 Peak magnetic flux density values of investigated points
由图8可知:采用数值计算1的面电流坐标计算得到的峰值磁通密度与有限元仿真结果比较接近,和试验测量值也较为吻合;数值计算2得到的峰值磁通密度与它们相比较小些,这主要是由于电枢上AB段和BB′段的y轴方向电流在各考察点产生z轴方向磁通密度,而AB段上的x轴方向电流分量产生-z轴方向磁通密度,A点位于-21 mm位置与-7 mm位置相比,在AB段上x轴分量电流产生的 -z轴方向磁通密度更大。由此可以看出,枢轨界面接触状态的变化将会直接影响各考察点的磁通密度值。
3 电枢运动状态下磁场分析
3.1 运动特性分析
电枢在膛内运动过程中,受到电磁推动力Fp、导轨和电枢间的摩擦阻力以及空气阻力共同作用,文献[17]通过研究表明空气阻力对于膛内电枢运动特性的影响较小,本文主要考虑摩擦阻力,表达式为
Ff=μFN,
(13)
式中:μ为摩擦系数,包含静态摩擦系数μs和动态摩擦系数μk,分别对应于静态摩擦力和动态摩擦力;FN为枢轨之间的接触压力,包含机械预紧力与电磁力。(7)式为静止状态下的枢轨界面电磁力计算公式,当电枢由静止变为运动状态时,lc将变为lt. 机械预紧力可以通过对图4中的枢轨界面接触压强在整个面上进行积分得到。
电枢的电磁推动力Fp=L′I2/2, 于是整个电枢和载荷受到的合力为
F=Fp-Ff.
(14)
速度可以表示为
(15)
式中:m为电枢和载荷的总质量。
位移可以表示为

(16)
式中:x0为发射时的初始位移。
输入电流波形如图9所示,对于30 mm口径轨道炮来说,上升时间为0.5 ms,峰值电流为1.5 MA. 与图6的脉冲电流相比,电流中增加了平台段,这是为了模拟实际发射电流波形,实际的发射电流是由多组脉冲电源通过时序放电的方式提供的[18]。
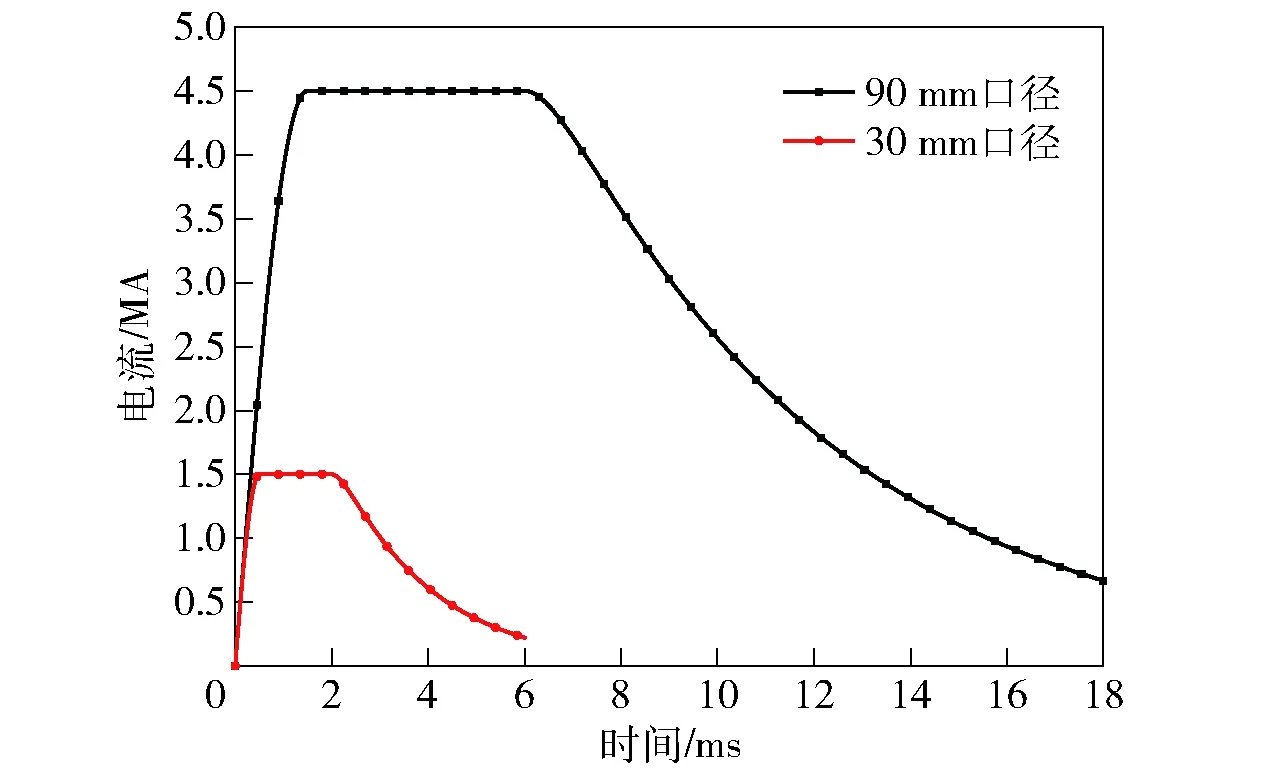
图9 输入电流曲线Fig.9 Input current curves
对于90 mm口径轨道炮来说,其几何尺寸是30 mm口径轨道炮几何尺寸的等比例放大,在本文中,二者保持相同的材料属性。将两种口径轨道炮的几何相似常数与输入电流幅值相似常数和时间相似常数保持一致,均为3,如图9所示:90 mm口径轨道炮的输入电流上升时间为1.5 ms,电流幅值为4.5 MA;30 mm口径轨道炮的长度为4 m, 90 mm口径轨道炮的长度为12 m.
同时对两种口径轨道炮进行接触压强分析,得到两种口径轨道炮的机械预紧力分别为16.266 kN和146.38 kN,30 mm和90 mm口径轨道炮电枢和载荷的总质量分别为370.37 g和10 kg,初始位移分别为0.15 m和0.45 m,取静摩擦系数和动摩擦系数分别为0.3和0.1,利用(7)式和(14)式~(16)式,可得速度和位移曲线如图10所示。从图10中可以看出:对于30 mm口径轨道炮来说,电枢出炮口时刻为3.09 ms,炮口初速为2 473 m/s;90 mm口径轨道炮电枢出炮口时刻为9.27 ms,炮口初速为2 470 m/s;对于30 mm口径轨道炮来说,t时刻电枢的运动速度与对应90 mm口径轨道炮3t时刻电枢的速度基本相同,能够实现两种口径轨道炮电枢速度匹配的近似模化。
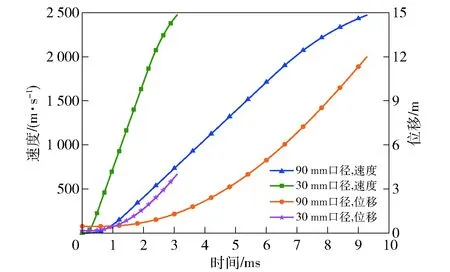
图10 速度和位移曲线Fig.10 Velocity and displacement curves
3.2 运动状态下枢轨电流分布
以30 mm口径轨道炮作为研究对象,分析在电枢运动状态下枢轨的电流分布情况。
设置导轨和电枢区域的边界条件和初始值[8],将图9中各个时刻的输入电流值和图10中的电枢速度导入COMSOL Multiphysic软件的PDE模块,对导轨和电枢区域的磁扩散方程进行求解,得到不同时刻各点的磁通密度值,再利用(5)式可以计算得到导轨和电枢区域的电流密度值。
取电枢运动过程的3个不同时刻0.5 ms、1.27 ms和2 ms进行考察,电流流线图如图11所示,由于速度趋肤效应,电流沿着导轨后端分布,且速度越大,距离电枢尾翼后沿越近,趋肤深度越小,与电枢尾翼后沿距离越远,趋肤深度越大。电流仅从与导轨接触的狭小区域流入电枢并扩散开来,比较图11中各时刻的电流线分布可以看出,速度趋肤效应对导轨中的电流分布有很大影响,但对电枢内部电流分布范围的影响不大,随着时间的增加,电枢内部电流逐渐从喉部区域向电枢前沿扩散,导轨和电枢接触区域的大部分基本没有电流通过。采用同样的方法分析90 mm口径轨道炮的枢轨电流密度分布,可以得到与30 mm口径轨道炮相同的结论。
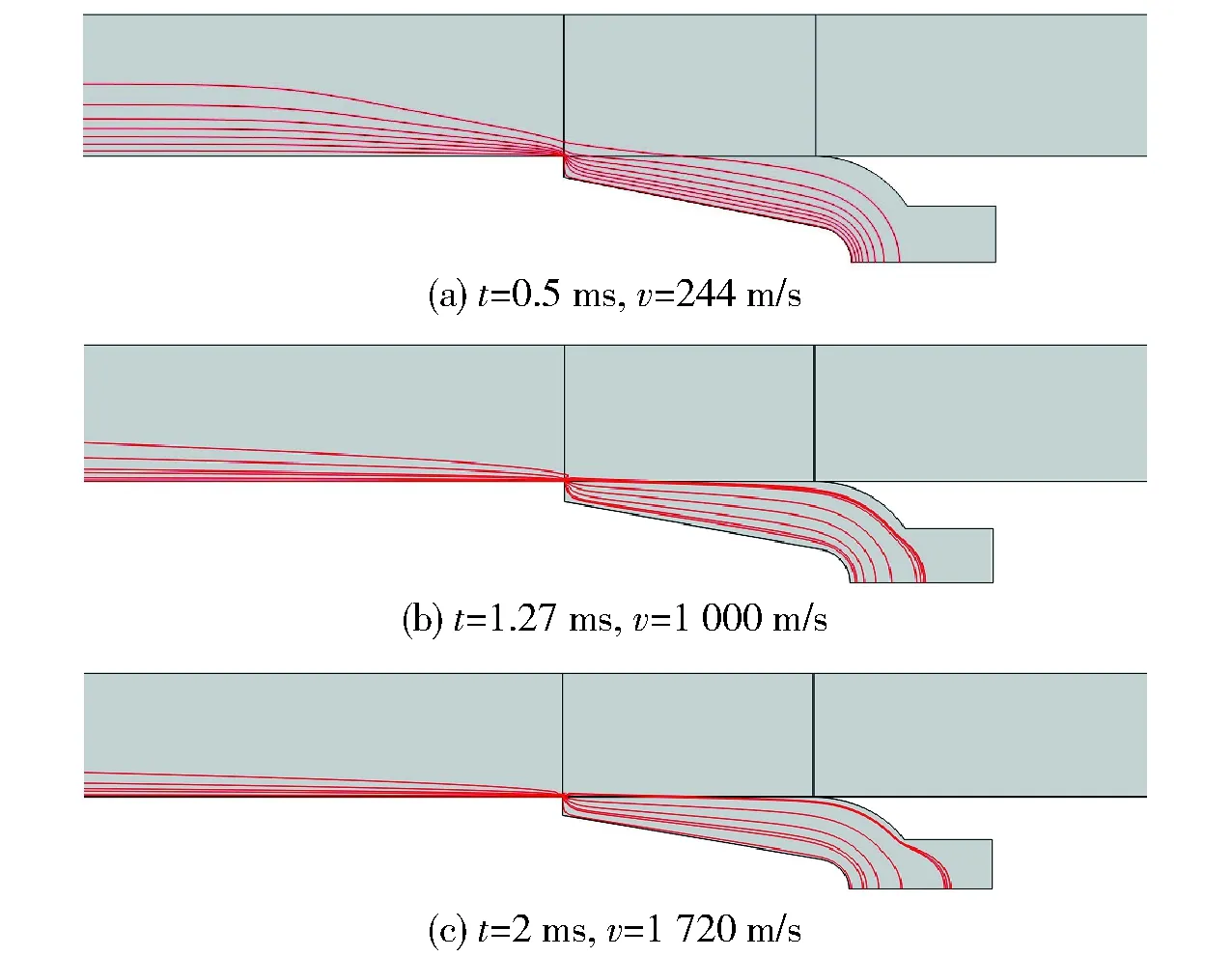
图11 0.5 ms、1.27 ms和2 ms时刻的电流流线图Fig.11 Streamline plots of current density at 0.5 ms, 1.27 ms and 2 ms
3.3 膛内磁场数值计算与有限元仿真
采用2.3节的方法,假设电枢内部电流为面电流分布,其中一半电枢的电流沿着图2中的电流面ABB′流动,以图11(a)中的0.5 ms时刻电枢电流分布为参照,不考虑电流在电枢内部的扩散效应。面电流坐标取值如下:A(-0.035 m,0.015 m)、B(0.012 m,0.006 m)、B′(0.012 m,0 m),对于导轨电流来说,取趋肤深度为4 mm,内外侧电流面电流密度比取9∶1. 取30 mm口径轨道炮前端中轴线上4个点为考察点进行分析,点1~点4的横坐标分别为30 mm、45 mm、60 mm和90 mm.
利用COMSOL Multiphysics软件进行仿真分析对比,通过设置导轨形状以及与电枢的接触长度来模拟运动状态,文献[19]推导出运动状态下枢轨之间的电流穿透距离为
(17)
式中:ρa和ρr分别为电枢和导轨的电阻率;θ为电枢尾翼倾角,θ=12°. 由图9和图10可以看出,0~2 ms时刻为电流峰值的平台段,电枢速度保持快速增加,该时间段内平均速度约为1 000 m/s,代入(17)式得到枢轨间电流穿透距离为0.5 mm.
结合图11(b)来设置仿真模型,考虑到电流在电枢内部持续扩散,按照电枢的实际尺寸作为仿真模型。对于导轨来说,取模型长度为150.5 mm(大于4.0倍口径),与电枢接触长度为0.5 mm,用来模拟运动过程的电流穿透距离;导轨宽度采取递减的方式,在炮尾位置宽度为5 mm,随着与电枢越近,宽度越小,与电枢接触长度末端位置的导轨宽度取1 mm.
数值计算和有限元仿真得到的各考察点磁通密度值如图12所示。由图12可以看出:0.5 ms时刻,数值计算得到各点的磁通密度值分别为3.19 T、1.46 T、0.80 T和0.35 T,有限元软件仿真得到各点的磁通密度值为2.74 T、1.43 T、0.87 T和0.39 T,除了点1之外,其他点的磁通密度基本吻合;由于在数值计算时没有考虑电流的扩散作用,电枢内部面电流各点坐标保持不变,因此各考察点的磁通密度曲线形状与输入电流值一致;在0.5~2 ms时刻,峰值磁通密度不变。对于有限元仿真结果来说,由于电流在电枢内部的扩散作用,0.5 ms后,考察点磁通密度值进一步增加;2 ms时,各考察点的磁通密度值分别为3.32 T、1.53 T、0.92 T和0.40 T,可以看出:对于考察点1和点2的作用比较明显;对于考察点3和点4来说,影响较小。

图12 各考察点磁通密度模Fig.12 Peak magnetic flux density values of investigated points
3.4 模化方法下磁场分布的相似性
为研究不同口径轨道炮膛内磁场分布的相似性,同时对30 mm和90 mm口径轨道炮进行仿真分析。对于30 mm口径轨道炮来说,仿真模型如3.3节所介绍,选择电枢前端中轴线上一系列考察点进行分析,各点横坐标从30 mm到175 mm,即1.0倍口径到6.5倍口径位置,考察点间隔为15 mm,即0.5倍口径长度。对于90 mm口径轨道炮来说,仿真模型的建立参照30 mm轨道炮,电枢按实际尺寸建模,导轨长度为450.5 mm,与电枢接触长度为0.5 mm,导轨宽度同样采用递减的方式,从炮尾位置的5 mm开始递减到导轨末端为1 mm. 考察点横坐标从90 mm到585 mm,各考察点间隔为45 mm. 两种口径轨道炮分别按图9中相应的输入电流进行仿真,取各自的平台段结束时刻(2 ms和6 ms)考察各点的磁通密度,按照3.3节的分析,该时刻各考察点磁通密度值最大,计算结果如图13所示。
为了更好地对不同口径轨道炮进行对比,图13中的横轴参数为各考察点横坐标与口径的比值。从图13中可以看出,两种口径轨道炮电枢前端的考察点磁通密度分布基本吻合,满足近似模化,具体到各点来说,30 mm口径轨道炮各考察点磁通密度都比相对应90 mm口径轨道炮各点稍大,从1.0倍口径到6.0倍口径位置,考察点峰值磁通密度分别为3.32 T、0.91 T、0.40 T、0.19 T、0.097 T和0.048 T,90 mm口径轨道炮各点为3.07 T、0.89 T、0.36 T、0.155 T、0.068 T和0.032 T. 随着与电枢距离的增加,各考察点峰值磁通密度迅速衰减,假设两种口径轨道炮考察点中的1倍口径位置点(30 mm和90 mm)为智能弹药的弹底位置,分别将其作为基准点,对其他各考察点与其的比值进行计算,结果见表1.
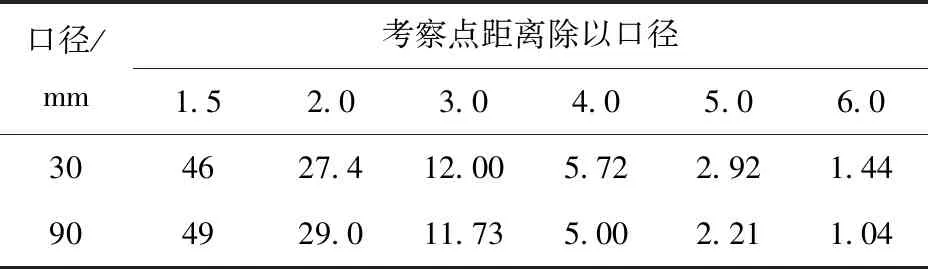
表1 各考察点和基准点峰值磁通密度比
对于30 mm口径轨道炮来说,2.0倍口径以内衰减速度最快,1.5倍口径位置的磁通密度只有1.0倍口径位置的46%;2.0倍口径位置的磁通密度只有27.4%,相当于考察点坐标从1.0倍增加到2.0倍,衰减率达到72.6%;从2.0倍口径位置开始,每增加1.0倍口径的距离,考察点磁通密度约为前者的50%;到6.0倍口径位置,磁通密度只有1.0倍口径位置的1.44%. 观察90 mm口径轨道炮的各点磁通密度比,也能够得到相同的结论。
3.5 讨论
由图12可以看出,电流在电枢内部由喉部区域扩散到电枢前沿区域会导致考察点磁通密度值的增加。下面分析电枢前沿长度变化对考察点的影响,将电枢前沿长度d1由13 mm减小为8 mm,减小的区域由非金属材料替代,假设电枢和载荷的总质量保持不变,这一改变不影响电枢在膛内的运动速度,采用与3.3节相同的导轨结构和枢轨接触长度,计算得到电枢前端各考察点的磁通密度模见表2.

表2 不同时刻各考察点磁通密度模
对比两种前沿长度的电枢在0.5 ms时刻的磁通密度值可以发现几乎没有区别,这说明此时电流主要集中于电枢喉部区域,电枢前沿区域电流较小;对比2 ms时刻可以发现,1.0倍口径考察点磁通密度有所减小,其他点基本没有影响,说明电流不会完全填满13 mm长的电枢前沿,只会扩散到一定长度;另外,电流在平台段时间电枢内部的扩散只对距离曲率圆心2.0倍口径以内的考察点有作用,2.0倍口径之外的考察点基本不受影响。
4 结论
本文从过盈C型电枢小口径轨道炮入手,分析静止状态下实际枢轨接触对电枢电流分布的影响,对电枢前端智能弹药部位考察点的磁通密度进行仿真和数值计算,并通过试验加以验证。在此基础上,分析了运动状态下膛内磁场分布特性,采用模化方法,对大口径轨道炮膛内磁场的匹配性进行了研究。得到以下结论:
1)电枢处于静止状态时,电流主要从枢轨实际接触区域前部边沿进入电枢,集中于电枢喉部区域。
2)电枢处于运动状态时,电流主要从电枢尾翼边沿的狭小区域进入电枢。通过设置几何相似常数和电流幅值相似常数与时间相似常数相等,可以实现不同口径轨道炮电枢速度和膛内磁场分布特性的近似匹配。在实际研究工作中,可以利用小口径轨道炮对大口径轨道炮进行近似模化。
3)对于电枢前端中轴线上考察点来说,各点磁通密度值随着与电枢曲率圆心距离的增加而迅速减小,从曲率圆心1.0倍口径距离到2.0倍距离时,磁通密度衰减率为72.6%,从2.0倍口径距离开始,每增加1.0倍口径的距离,磁通密度大约衰减50%,6.0倍口径考察点的磁通密度只有1.0倍口径考察点的1.44%.
4)在电流波形的平台段,电流会从电枢的喉部区域扩散到电枢前沿部分,对距离曲率圆心2.0倍口径以内的考察点磁通密度有一定的增加作用。
