基于概率定义扩展样本的机载雷达空间和时间相关海杂波数据仿真方法

毛辉煌， 谢文冲， 徐鹏， 刘畅

(1.空军预警学院， 湖北 武汉 430019; 2.中国人民武装警察部队警官学院， 四川 成都 610000)

0 引言

海杂波抑制性能是机载预警雷达在系统设计和信号处理方案选择过程中必须考虑的因素。而研究海杂波性质对于提高海杂波抑制性能具有重要的参考意义和理论价值。海杂波受多种因素影响，特征变化较大，因此需要统计大量的海杂波实测数据，提取海杂波更加深入的特征。然而持续采集海杂波实测数据会消耗大量的人力和财力资源，尤其是对于机载预警雷达。逼真的机载雷达海杂波数据仿真方法可以模拟不同海况下的海杂波数据，对于机载预警雷达研制以及目标检测算法的选择[1]具有非常重要意义。

机载雷达海杂波的仿真与模拟主要关注海杂波的分布形式和相关特性。海杂波是由雷达分辨单元内大量散射体的回波矢量叠加而成的，但其复杂多变，与雷达工作频率、分辨率、擦地角和照射区域的海情等多种因素都有关系。为此，几十年来国内外学者均对海杂波进行了深入研究，结合数学理论和实测数据的分析，提出了瑞利分布、韦布尔分布、对数正态分布、K分布、KK分布[2]、WW分布等分布模型。而机载预警雷达海杂波常常表现出空间和时间(简称空时)二维相关性[3]，其中，时间相关性对于目标检测有一定影响[4-5]，研究中常采用功率谱密度作为其等效替代研究对象，一般采用高斯功率谱模型，而当前对海杂波的空间相关性研究较少。一般来说，空间相关性和大尺度的波浪起伏有关，决定海杂波的平均功率，一般采用指数衰减模型。

到目前为止，国内外主流的海杂波仿真产生方法主要有两种：一种是无记忆非线性(ZMNL)变换法[6]，另一种是球不变随机过程(SIRP)[7]。上述两种方法能够在一定程度上仿真出符合分布特性要求和相关性要求即频谱要求的杂波，但仍然存在一些局限，例如，ZMNL变换法的非线性变换导致不能独立控制杂波的幅度分布特性和相关特性，而SIRP方法虽然能单独控制分布特性和相关性，但是其无法仿真对数- 正态分布海杂波。此外，文献[8]在SIRP方法以及海杂波成分分析的基础上，运用迭代公式产生了相关的海杂波斑纹分量，生成了空时相关海杂波，但该方法要求产生两个自相关函数相同，互相关函数为0的随机序列，增加了仿真的难度。文献[9]利用外推的方法提高了海杂波幅度分布和功率谱的准确性，但该方针耗费的时间较长。文献[10]基于Kronecker积产生了二维相关杂波，但该方法产生的幅度分布准确度欠佳。

针对传统海杂波方法存在的问题，本文基于概率密度函数的定义，在大量试验情况下，利用频数除以试验总次数约等于概率的假设，得到满足分布要求的随机矩阵X；随后通过传递矩阵将预设的空时相关杂波的二维相关性传递给X，即进行矩阵内部排序，最后得到满足空时相关要求的特定分布杂波。

1 传统方法

1.1 ZMNL方法

图1为ZMNL方法的实现流程图，其中x1为高斯随机变量，x2为预设分布随机变量。该方法由以下两个步骤组成：

1)通过二维线性滤波器对N(m,n)进行二维滤波，得到满足空时相关性的矩阵C(m,n)，其中：N(m,n)为二维高斯矩阵，C(m,n)为二维相关高斯矩阵；m为矩阵的行数，对应杂波的空间单元数；n为矩阵的列数，对应单个杂波空间单元内的采样数。

2)对C(m,n)进行非线性变换得到最终结果。

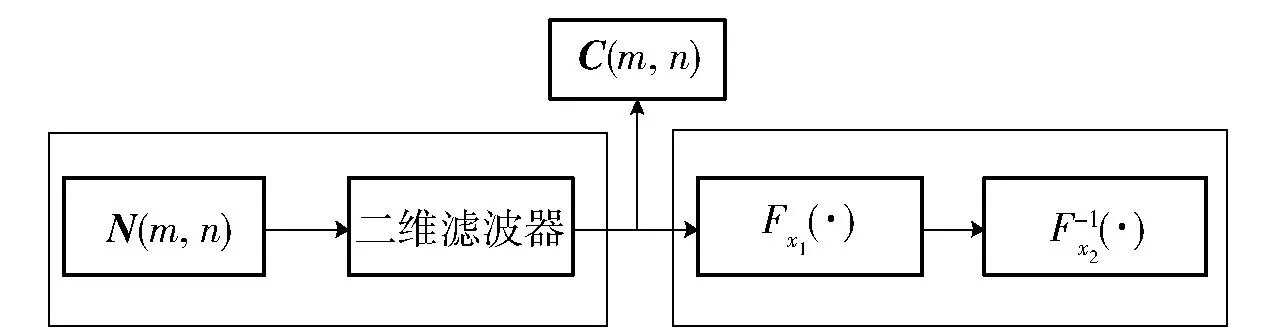
图1 ZMNL变换法流程图Fig.1 Flowchart of ZMNL

ZMNL方法很容易形成快速算法，但非线性变换将改变C(m,n)的相关性，相关性的失真度取决于杂波模型。 因此，ZMNL方法无法独立控制幅度分布和相关性。

1.2 SIRP过程

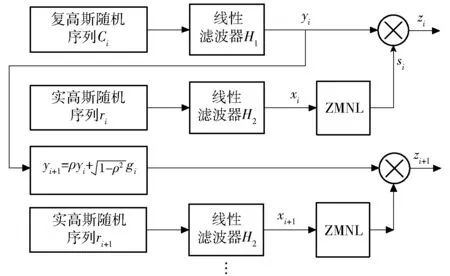
图2 SIRP方法流程图Fig.2 Flowchart of SIRP

图2为通过SIRP方法产生空时相关海杂波数据的实现流程图[5]，具体步骤介绍如下：

2)由实高斯随机序列ri+1生成散斑分量xi+1；

3)zi+1=yi+1×xi+1，zi+1为第i+1个距离单元的海杂波信号；

4)重复上述3个步骤来产生下一个距离单元的海杂波。

由于对数正态分布不满足非负单调递减特性，因此SIRP方法不能模拟对数正态分布杂波。另外，由于需要求解非线性方程，导致SIRP方法的计算量较大。

下面结合文献[6-7]进一步说明3种方法的差异，具体见表1.

表1 方法比较

1)ZMNL方法:主要是先通过线性变换产生相关高斯序列，再通过非线性变换产生符合分布的相关序列，这种做法的优点是简单快速，但同时应看到非线性变换同时也会导致相关性的变化，即该变换不能比较容易地同时控制相关性和幅度分布特性，这是因为变换前后的相关系数具有比较复杂的关系，不同的分布关系也不同，另在K分布产生过程中，对于K分布的参数选择要求为半整数，这进一步影响了利用该方法进行海杂波仿真的精度。

2)SIRP方法:主要是基于球不变随机向量的性质，该方法可以同时控制杂波的相关性和幅度分布特性，但不是所有的分布类型都符合SIRP方法产生的条件，例如对数正态分布，就不满足产生的条件，另外SIRP方法计算量较大，易受序列阶数和自相关函数的限制。

3)扩展方法:通过概率密度函数直接产生对应分布变量，同时利用相关性的传递性得到符合分布的相关序列，对任意给出概率分布函数的分布类型都是可实现的，同时产生速度相对较快，但其幅度分布特性的精度与杂波样本数目以及取整规则有关，同时受计算机内存所限。

2 海杂波的相关性

2.1 时间相关性

功率谱密度常用来描述时间相关性，常用的功率谱模型为高斯谱和N次方谱，而高斯谱是目前应用最多的功率谱模型，其形式为

(1)

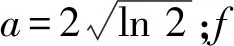
R(τ)=e-σcπ2τ2,

(2)

式中：σc为海杂波频率分布的均方根值；τ为时延。

2.2 空间相关性

海杂波的空间相关性与海面的状态密切相关，海杂波的相关距离和风速、风向以及重力加速度有关。文献[11]对影响海杂波空间相关性的因素，如海况、距离分辨率和采样率等的关系作了深入分析。常见的描述海杂波空间相关性的数学模型如下：

(3)

式中：第1个模型和第2个模型为幂律模型，第3个模型为自然指数衷减模型；m为距离单元序号；Ncor为相关距离单元数目。

3 基于概率定义扩展样本的海杂波仿真方法

针对传统杂波仿真方法存在的频谱展宽、幅度特性拟合精度欠佳及所仿杂波类型受限的问题，提出了基于概率扩展样本的蒙特卡罗杂波直接产生方法，简称扩展方法。该方法首先基于概率定义扩展成样本后得到随机非相关分布杂波，然后通过对相关矩阵进行Cholesky分解[12]产生相关杂波，再通过传递向量，将相关性传递给随机非相关分布杂波，得到相关分布杂波。

3.1 扩展方法流程图

扩展方法流程图如图3所示。

图3 扩展方法流程图Fig.3 Flowchart of extension method

下面根据流程图顺序给出相关的理论证明。

3.1.1 产生二维相关高斯杂波

由于高斯分布具有在相关(线性)变换后仍然保持高斯特性的优良性质，故采用高斯分布作为产生相关样本杂波的起始样本。

设RM×N为M×N阶高斯随机矩阵，以下简写为R. 首先根据空间相关函数和时间相关函数生成对应的空间相关托普利兹矩阵Ms和时间相关托普利兹矩阵Mt，然后对Ms和Mt进行Cholesky分解，得到如下结果：

(4)

式中：A为空间相关矩阵Cholesky分解后得到的矩阵；B为时间相关矩阵Cholesky分解后得到的矩阵。

然后进行相关变换，即G=ARB，G为满足时空二维相关性的高斯随机矩阵，R为高斯随机矩阵。其相关证明如下：

时空二维相关分布产生，RM×N为M×N阶高斯随机矩阵，以下简写为R，其相伴矢量为

vec(R)=[R(1,1),R(1,2),…,
R(1,n),…,R(M,1),…,R(M,N)]T.

(5)

而E(vec(R)(vec(R))T)=IMN×MN，设二维相关矩阵的指定协方差矩阵Ms-t=Mt⊗Ms,其中⊗为Kronecker积，而Ms和Mt分别为空间相关协方差矩阵和时间相关协方差矩阵：

(6)

vec(GM×N)=B⊗ATR=
[G(1,1),G(1,2),…,G(1,N),…,G(M,1),…,G(M,N)]T,

(7)

则G的协方差矩阵为

cov (G)=E(vec(G)(vec(G))T)=
E[(BT⊗Avec(R)) (BT⊗Avec(R))T]=
BT⊗Avec(R)(vec(R))TBT⊗A=
(BBT)⊗(AAT)=Mt⊗Ms.

(8)

3.1.2 相关性的传递

杂波的时间相关性主要由值的排列顺序和值的大小决定，但是前者是决定因素。

传递方法的本质是使两个序列内部值大小的排序呈现一致性，假设有两个序列X、Y，X为任意随机样本序列，Y为X值大小的顺序排行序列，定义样本相关性如下：

(9)

式中：RX(1)、RY(1)分别为序列X中、序列Y中延迟为1时的相关系数，并且由(9)式可知，两个相关性变化趋势是一致的。下面分别将两个序列中第S个位置的值和第T个位置的值进行交换，交换后，样本相关性分别为RX′(1)和RY′(1)：

(10)

若RX′(1)>RX(1)，则X(T)-X(S)和X(S+1)-X(T+1)均大于0.

因为Y代表X中对应位置值的大小顺序，所以Y(T)-Y(S)和Y(S+1)-Y(T+1)也均大于0.

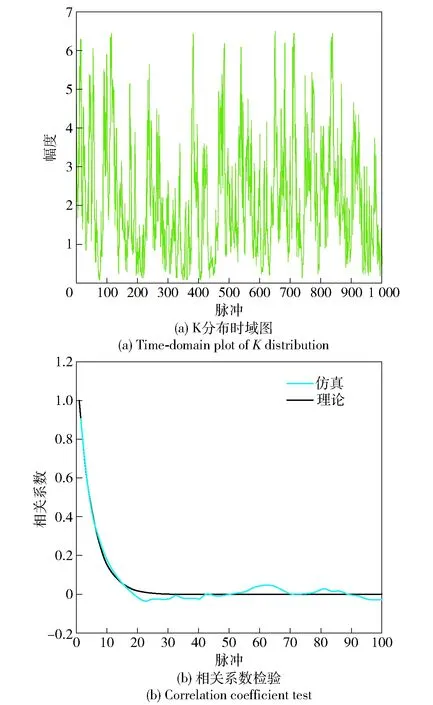
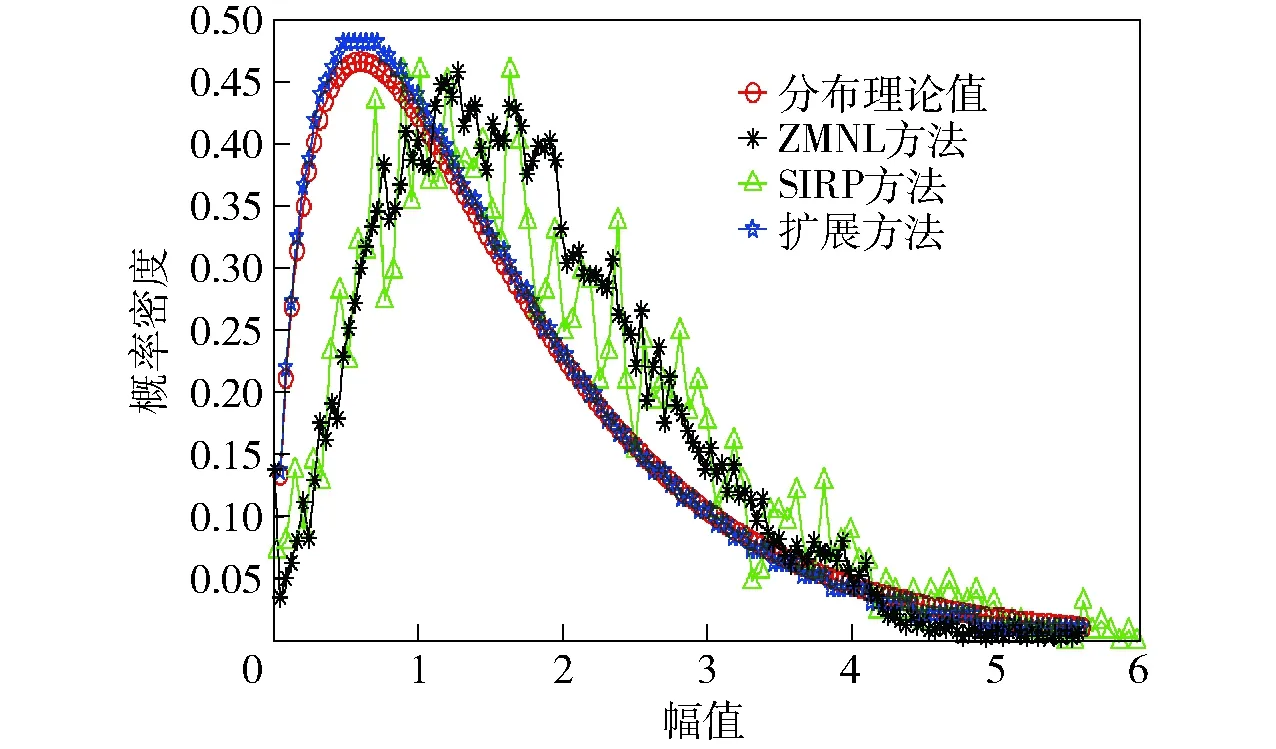
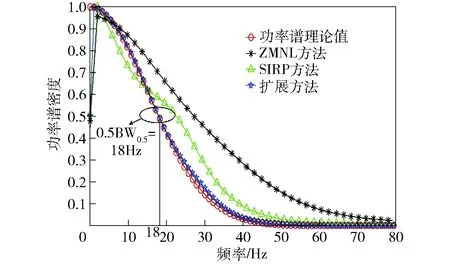
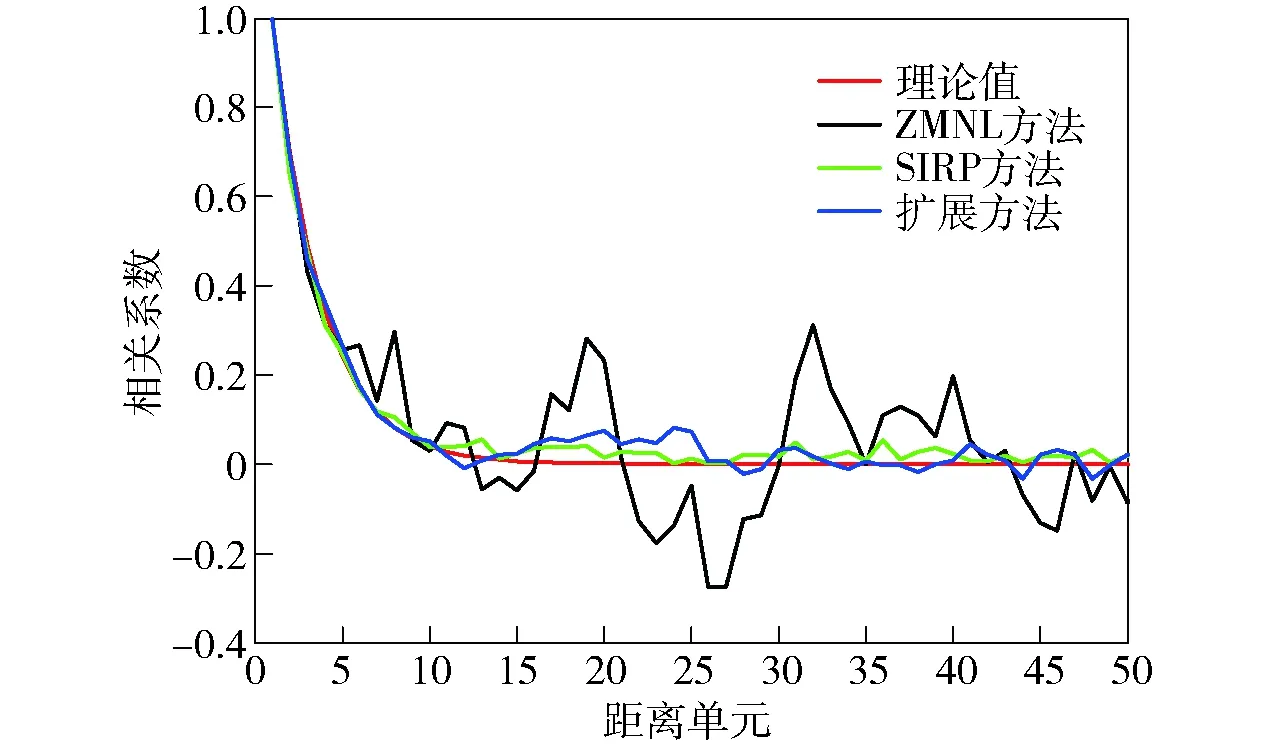
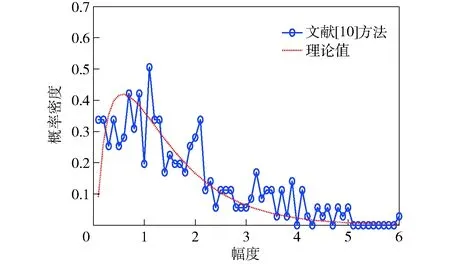
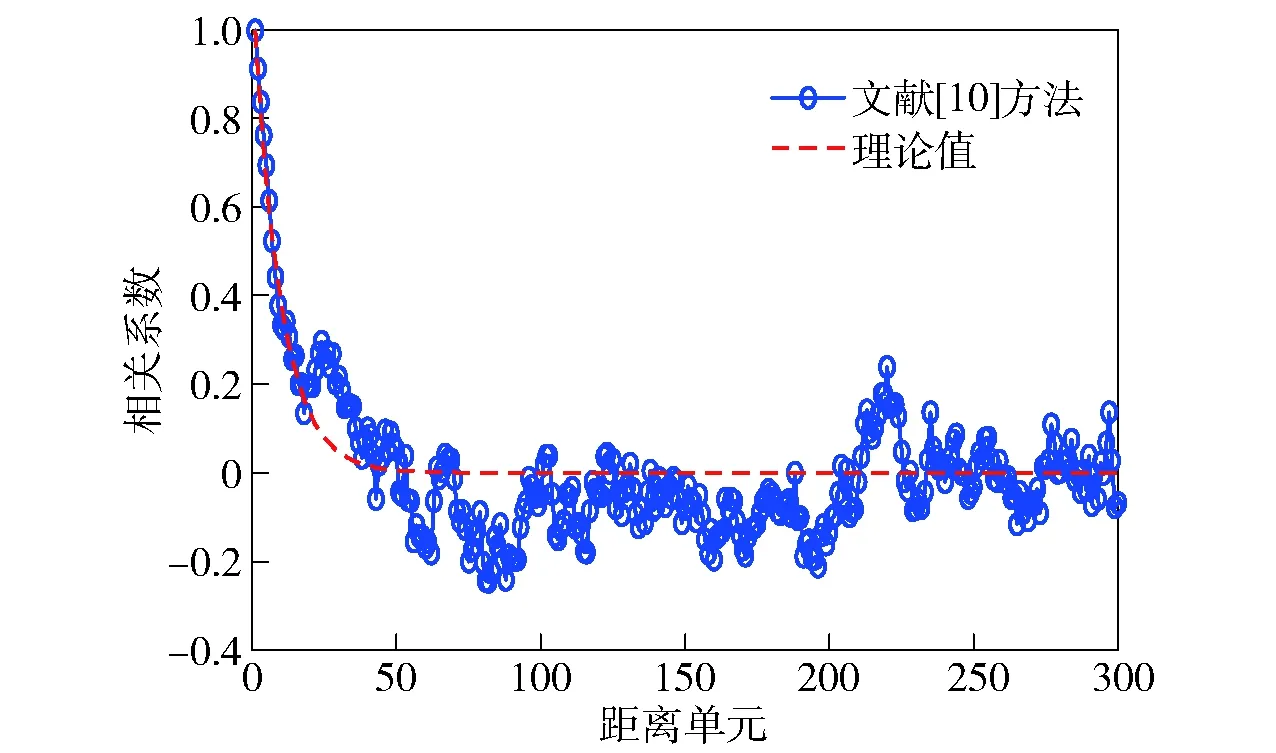
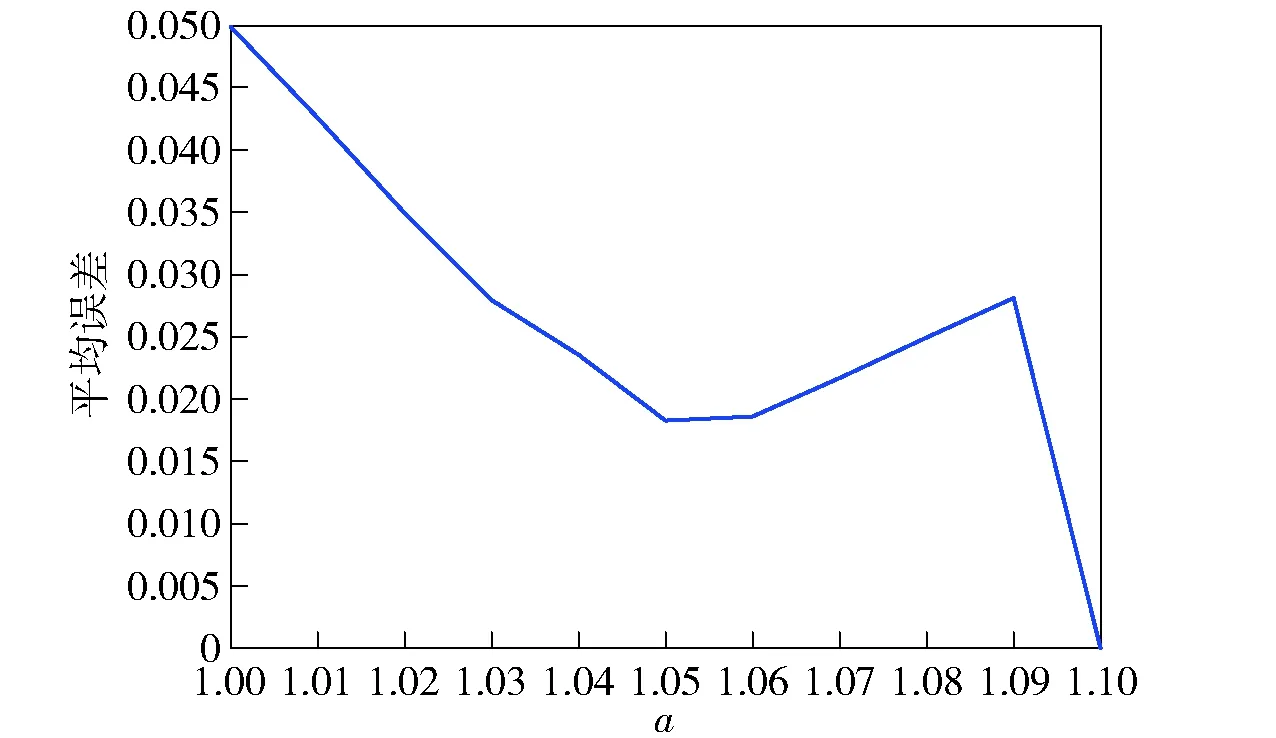
若RX′(1)

上述证明可以表明任意序列和其排列顺序序列的自相关具有相同的变化趋势，并且两个序列内部进行相同规则排序时，其相关性变换趋势一致。

这就证明了两个序列可以通过样本顺序序列传递相关性的可行性。

为了进一步说明方法的有效性，下面通过仿真证明该方法的正确性，分别采用瑞利分布、对数正态分布、韦布尔分布、K分布4种分布来验证，4种分布的参数设置如表2所示。表2中，σRayleigh是瑞利分布的标准差，σlog是对数正态分布的标准差，Ulog是对数正态分布的中值，UWeibull是韦布尔分布的中值，bWeibull是韦布尔分布的形状参数，vK是K分布中的尺度参数，bK是K分布中的形状参数。

表2 参数设置

图4～图7仿真证明了该方法的有效性，另外，在同一类分布的杂波中，改变内部序列值的顺序并不能改变其分布特性，这一点是众所周知的，在此就不再赘述。因此该方法在理论上是可行的。

图4 瑞利分布相关性质检验Fig.4 Correlation property test for Rayleigh distribution

图5 对数- 正态分布相关性质检验Fig.5 Correlation property test for log-normal distribution

图6 韦布尔分布相关性质检验 Fig.6 Correlation property test for Weibull distribution

图7 K分布相关性质检验 Fig.7 Correlation property test for K distribution

3.2 实现步骤

海杂波数据仿真实现步骤：

给定产生杂波的基本条件：概率密度函数f(x)；离散时间范围0，d，…，(n-1)d；概率密度函数向量F(x)=[f(x1)f(x2) …f(xi) …f(xn)]，i=1,2,…,n,n为概率密度函数的样本个数。

步骤1产生符合分布的随机矩阵：

1)产生对应的随机分布向量: [xixi…xi] 一共T(xi)个，T(xi)=「f(xi)×Me⎤，「·⎤代表向上取整,Me为实验总次数；

步骤2产生符合二维相关的样本随机矩阵：

2)根据时间相关函数R(τ)和空间相关函数R(m)生成对应的时间协方差矩阵Mt和空间协方差矩阵Ms；

3)对Mt和Ms进行Cholesky分解得到上三角矩阵A和下三角矩阵B；

4)二维相关处理Q=ARB，得到满足空时相关二维相关性的杂波Q.

步骤3传递相关性：

Q映射W，得到满足空时二维相关性的K分布杂波Z.

4 仿真分析

K分布模型不仅能够很好地满足观测海域单点的幅度统计特性，而且其本身的复合结构具有脉间相关性能，是目前公认比较能够精确描述雷达海杂波的模型。因此，本节利用K分布模型验证所提方法的有效性。K分布的概率密度函数为

(11)

式中：c为尺度因子；v为形状因子；Kv-1(·)为第2类修正Bessel函数；Γ(·)为伽马函数。时间相关模型选择高斯模型，空间相关模型选择指数衰减模型。根据对机载预警雷达海杂波实测数据的分析[13]，其典型参数值设置为c=1，v=1，杂波功率半谱宽BW0.5=18 Hz，空间衰减系数ρ=0.3.

4.1 仿真数据验证

4.1.1 实验1：空时相关杂波二维图

图8给出了仿真得到的空时海杂波二维数据，图9给出了对应的空时相关性情况。从图4中可以看出，利用所提方法可以产生具有显著空时二维相关性的海杂波数据。

图8 空时二维相关海杂波Fig.8 Spatial-temporal correlated sea clutter

图9 海杂波二维相关系数Fig.9 Two-dimensional correlation coefficient of sea clutter

4.1.2 实验2：杂波幅度统计分布

图10给出了通过传统方法和所提方法仿真得到的杂波数据幅度统计分布。从图10可以看出，传统ZMNL方法和SIRP方法仿真产生的K分布杂波幅度相较于理想值存在一定偏差，这是因为传统方法在产生过程中均应用了非线性变换，而非线性变换会同时改变杂波的相关性和幅度分布特性。相反，所提方法产生的海杂波数据杂波幅度分布特性更加接近理想值。

图10 3种方法仿真幅度分布值和理论值比较图Fig.10 Comparison of simulated and theoretical amplitude distributions of three methods

4.1.3 实验3：杂波功率谱分布

图11给出了通过传统方法和所提方法仿真得到的杂波数据功率谱密度分布。从图11可以看出，传统ZMNL方法和SIRP方法产生的K分布海杂波功率谱密度图相较于理想值有一定偏差。SIRP方法相较于ZMNL方法更加接近理想值，而ZMNL方法产生的功率密度谱相对于理想值有一定的展宽，这是因为ZMNL变换导致变换前的相关序列的相关性减弱，进而使该方法产生的功率谱密度展宽。而所提扩展方法产生的杂波数据半功率谱宽约为18 Hz，更加接近于理论值。在这里需要说明的是，由于机载雷达采集的单点试验数据有限，不足以展开对实测海杂波数据的功率谱密度比较，因此无法通过实测数据比较该方法对于机载雷达实测海杂波功率谱的拟合程度，在大量研究表明海杂波功率谱具有高斯谱形状的情况下，该文通过比较证明该方法可以仿真具有高斯功率谱形状的海杂波数据，并且具有优势。

图11 3种方法仿真功率谱密度和理论值比较图Fig.11 Simulated and theoretical power spectrum densities

4.1.4 实验4：空间相关性

图12给出了3种方法仿真得到的空间相关系数和理论空间相关系数之间的对比图。从图12可以看出：所提扩展方法产生数据的空间相关性逼近于理论值；值得注意的是，随着距离单元数目的增加，ZMNL方法的拟合效果变差。

图12 仿真空间相关系数和理论值比较结果Fig.12 Simulated and theoretical spatial correlation coefficients

4.1.5 实验5：与文献[10]方法的比较

从图13～图15可以看出，文献[10]的方法可行性，虽然仿真的准确度有所欠缺，但依然不失为一种产生空时相关杂波的好方法。

图13 文献[10]幅度分布和理论值比较图Fig.13 Amplitude distribution in Ref.[10] and theory distribution

图14 文献[10]归一化功率谱和理论值比较图Fig.14 Normalized power spectrum density in Ref.[10] and theoretical value

图15 文献[10]空间相关性和理论值比较图Fig.15 Spatial correlation coefficient in Ref.[10] and theoretical value

4.1.6 实验6：误差分析及方法局限

分析当K分布的2个参数变化时，仿真杂波幅度分布与理论分布的平均误差值，具体如图16、图17所示。

图16 尺度参数a的平均误差曲线Fig.16 Mean error curve of scale parameter a

图17 形状参数v的平均误差曲线Fig.17 Mean error curve of shape parameter v

通过该方法仿真，当参数选择不当例如尺度因子过大，或者样本数量过大时，扩展方法因为内存不足，是失效的，这就对电脑内存提出了一定的条件，因此需要谨慎选择参数和样本数量，防止内存不足，无法使用该方法。这会限制该方法的使用范围，不同性能的电脑，参数和样本数量的可选择范围也是不一样的，需要通过进一步的实验，同时由于参数的限制，也就导致了某些场景的不可复现。例如尺度因子过大，高海情海杂波就无法模拟。

4.2 实测数据验证

本节采用某机载雷达实测数据进行分析。在对海模式下机载雷达采用非相参体制，一个脉冲重复周期内仅包含3～5个脉冲，因此无法进行杂波谱宽的分析。下面重点从空间相关性的角度进行分析验证，如图18所示。由图18可知，仿真数据的空间相关性和实测数据的空间相关性基本吻合，证明了该方法可以仿真与实际空间相关性一致的杂波数据。

图18 基于实测数据的海杂波空间相关系数对比Fig.18 Simulated and measured spatial correlation coefficients

4.3 运算量分析

表3给出了在2.67 GHz主频、2G内存条件下不同方法的计算机仿真所需时间。由表3可以看出，4种方法的运算时间大小排序为：文献[9]>SIRP方法>ZMNL方法>扩展方法。因为扩展方法中产生的随机数运算量很小，而SIRP方法和ZMNL方法涉及随机数程序的运算量相对较大，并且SIRP方法中还涉及到了非线性方程的求解问题，进一步增大了运算量。文献[9]在SIRP方法和ZMNL方法基础上还有功率谱的迭代过程，运算量显著增大，因此，在运算次数一定情况下，文献[9]运算时间最长，而新方法产生相关性的步骤不涉及随机数，可以不用进行蒙特卡罗仿真，节省了运算时间。在蒙特卡罗仿真次数为10 000次时，扩展方法的运算时间比文献[9]方法和SIRP方法少了两个数量级，比ZMNL方法少了一个数量级。

表3 运算时间比较

5 结论

本文提出了基于概率定义扩展样本的空时二维相关机载雷达海杂波产生方法。仿真和实测数据分析结果表明，在幅度分布、功率谱宽和空间相关性等方面，所提扩展方法均能产生满足要求的海杂波数据。同时在运算量方面，扩展方法的运算时间远远小于传统方法。因此本文所提出的扩展方法可以用于产生逼真的机载雷达海杂波数据，具有一定的工程应用前景。