带有不同视场约束的多导弹分布式协同制导
2019-04-17叶鹏鹏张蛟李银伢戚国庆盛安冬
叶鹏鹏, 张蛟, 李银伢, 戚国庆, 盛安冬
(1.南京理工大学 自动化学院, 江苏 南京 210094; 2.63961部队, 北京 100012)
0 引言
随着网络化协同防空反导防御体系的发展,单枚导弹打击目标受到越来越多的挑战[1];同时,多导弹协同作战由于具有突防能力强、毁伤概率高、能够饱和攻击等特点,近年来逐渐成为导弹作战的研究热点[2-4]。
多导弹协同作战中的齐射攻击,即各枚导弹同时命中目标,不仅要求导弹能够命中目标,还强调命中的同时性,这是协同制导问题的重点。这里的“同时”允许有一定的时间误差,只要来袭导弹之间到达该目标的时间间隔小于反导系统发射完一波拦截弹后再次发射所需要的准备时间,就可以达成突防的效果。众多学者对此已进行了较深入的研究,文献[5]针对反舰导弹首先提出了一种遭遇时间可控协同制导律(ITCG),通过预设攻击时间可实现反舰导弹的齐射攻击。文献[6]针对固定目标,以剩余时间为协调变量,提出一种有限时间协同制导律以实现对目标的齐射攻击,该制导律从理论上考虑了导弹过载饱和的影响。文献[7]研究了有限时间下多导弹的齐射攻击问题,所提制导律除在导弹上施加法向过载外,也要求各导弹切向加速度可调。文献[8]使用反馈线性化方法,基于多智能体一致性理论,实现了固定及切换拓扑下针对多个目标的协同制导。文献[9]考虑了通信存在丢包和时延等情形的多导弹协同制导问题。上述时间约束制导律在设计时均主要关注各导弹遭遇时间的变化,其目的是确保各枚导弹同时到达目标。然而分布式协同制导要求导弹在飞行过程中必须保证导引头对目标的锁定,即目标应始终处于导引头视场(FOV)范围内;否则,当某枚导弹的导引头丢失目标时,不仅无法保证此枚导弹能够击中目标,而且由于弹间通信网络信息交互,甚至会影响其余导弹命中目标,降低多导弹系统整体的打击能力。因此,实际工程中在设计时间约束协同制导律时,考虑导弹FOV约束至关重要。
目前针对导弹存在FOV约束的研究主要是考虑单枚导弹制导的情形[10-13]。对于多导弹协同制导,文献[14-15]在设计时间约束协同制导律时考虑了末端视线角约束,此类协同制导律在设计时并未从理论上分析FOV约束对协同制导的影响,而是通过对所设计的导引律进行分析来选择合适的参数,以保证导弹飞行过程中对目标的锁定。此类方法依赖于多导弹的初始攻击阵位,具有一定的保守性。文献[16]设计了一种基于偏置比例导引(BPNG)的协同制导律,以遭遇时间为协调变量,实现了FOV约束下多反舰导弹的遭遇时间一致。文献[17]研究了末端任意攻击角限制下多反舰导弹的分布式齐射攻击,所提协同制导律能满足FOV的约束条件。然而文献[16-17]中要求各导弹导引头具有相同的FOV约束,本质上是单枚导弹存在FOV约束[11]的推广;此外,文献[16-17]中所考虑的各导引头具备较大的视场角(90°),对于配备捷联式导引头等视场较窄的导弹,此类制导律则难以适用。因此,文献[16-17]中所提协同制导律并不能直接用于带有不同FOV约束的多导弹协同制导。
尽管文献[18-19]对异类导弹协同制导的可行性进行了研究,然而目前关于不同FOV约束下多导弹协同制导的研究尚且较少。进行齐射攻击的导弹往往来自多个平台,如空基、陆基、海基等;即使来自同一平台,导弹种类也可能不同。异类导弹通常具有不同的FOV约束,如部分高性能导弹通常搭载大视场导引头,某些低性能导弹搭载的导引头FOV范围往往较窄。因此,本文研究了带有不同FOV约束的多导弹协同制导问题,所提制导策略分为两个阶段:第一阶段为协同制导阶段;第二阶段为独立导引阶段。本文侧重研究了第一阶段,即协同制导阶段,并通过仿真示例对所提制导策略进行了验证。
1 问题描述
三维空间的导引可以解耦成二维纵向平面与横侧向平面的导引。由于导弹在接近目标时横侧向平面的运动可以忽略,本文考虑二维纵向平面内N(N>1)枚异类导弹协同制导。假定目标固定,典型固定目标有地面重要设施、交通枢纽等;此外,考虑舰船运行速度远远小于导弹飞行速度,一般也将舰船近似成固定目标,因此本文研究的导弹类型包括了对地及反舰导弹。假设各导弹为质点模型,采用气动力布局;飞行过程中导弹所受合力对轴向速度大小的影响可忽略不计,即假设导弹轴向速度大小不变,仅能改变导弹的法向过载,当各导弹均脱离上升段后开始协同制导。
异类导弹往往搭载不同性能的导引头,如图1所示,某类高性能导弹搭载了大视场导引头;而某类低性能导弹搭载的导引头视场较窄,如红外导引头等无源导引头或者捷联式导引头。若以各导弹中的最大FOV范围作为统一约束,则有可能使配备小视场导引头的导弹在飞行过程中丢失目标;反之,若以各导弹中的最小FOV范围作为统一约束,则必然会限制高性能导弹的机动范围,浪费多导弹系统整体的攻击能力。因此,异类导弹协同制导律在设计时需要考虑导弹不同的FOV约束对各自的影响。
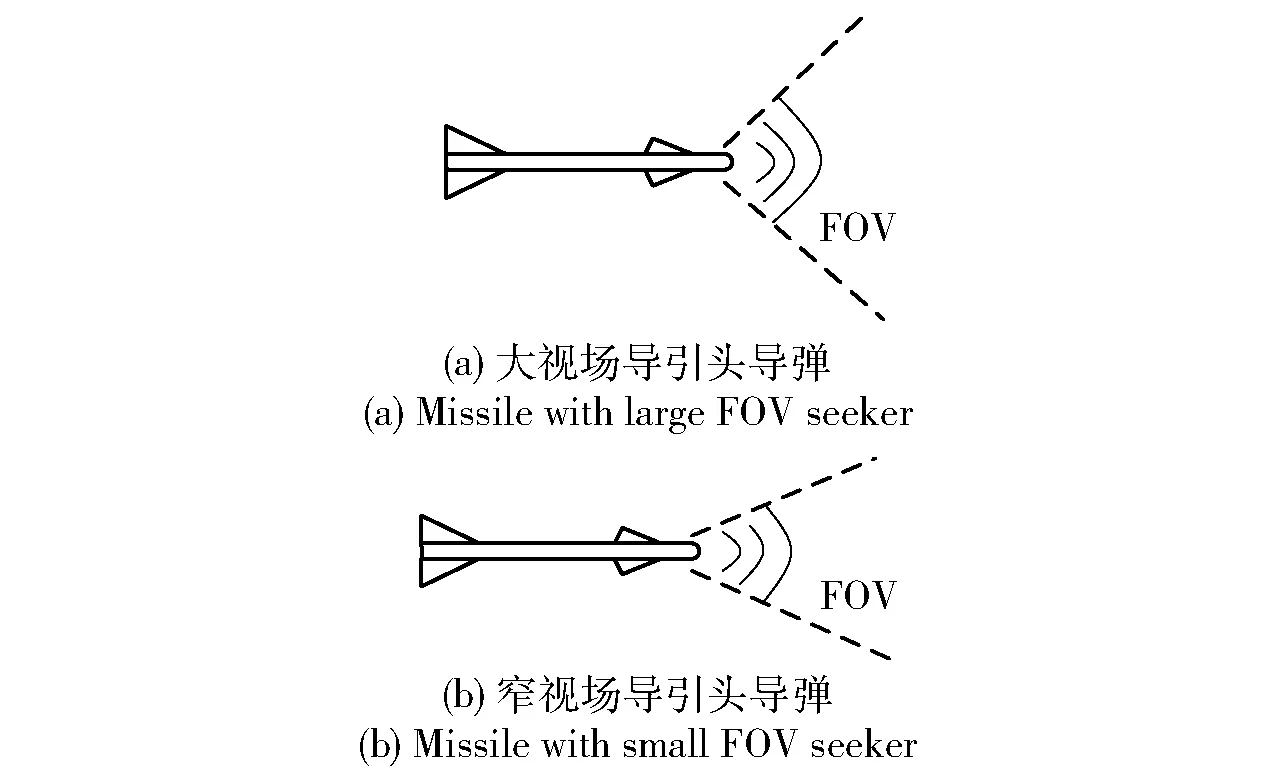
图1 搭载不同导引头的异类导弹Fig.1 Missiles equipped with different seekers
1.1 运动学建模
导弹与目标的导引几何关系如图2所示。图2中:T表示目标,Mi表示导弹i,ri、vi和ai分别表示导弹i的弹目距离、轴向速度和法向过载,ai垂直于导弹的轴向方向;ϑi、θi和μi分别表示导弹i的视线角、弹道倾角和前置角。
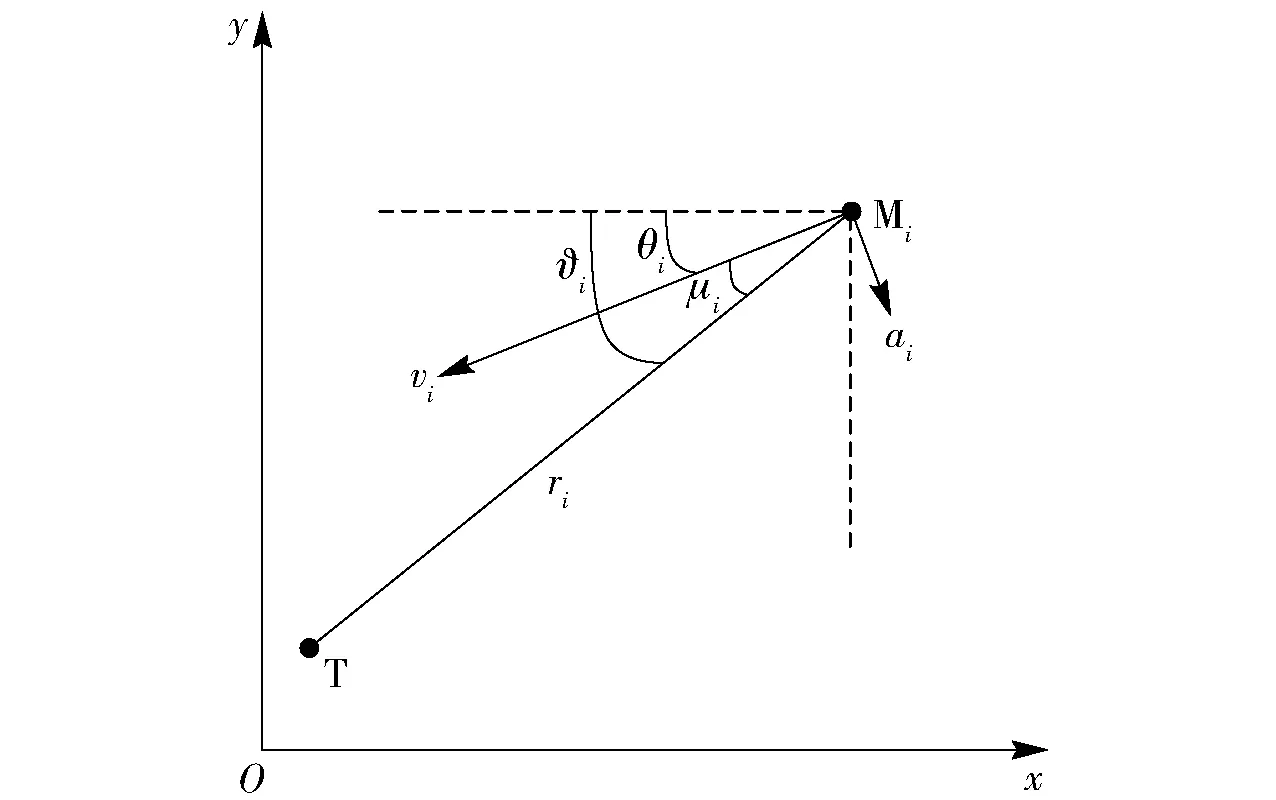
图2 导弹i与目标几何关系示意图Fig.2 Geometrical relationship between ith missile and target
导弹i相对目标的运动方程可表示为
(1)
由图2可知,μi(t)=ϑi(t)-θi(t). 本文考虑μi(t)∈[0 rad,π rad],即ϑi(t)≥θi(t)时的情形;而μi(t)∈[-π rad,0 rad)可认为是μi(t)∈[0 rad,π rad]时的对称情形。
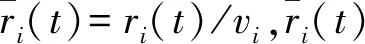
(2)
结合(1)式与(2)式,可得(3)式:
(3)

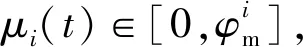
(4)
需要说明的是,由于本文主要研究不同FOV约束对协同制导过程的影响,异类导弹差异主要在于各导弹FOV范围与速度的不同,导弹其他特性的差异未重点考虑。
1.2 协同制导问题

根据多导弹对目标齐射攻击的要求,定义任意导弹i与导弹j,且i≠j,当相关变量满足(4)式与(5)式条件时,多导弹实现协同制导:
(5)

(6)


(7)
同时可得线性化输入为
ui
(8)
经反馈线性化后,可得导弹i的线性相对运动方程如(9)式所示:
(9)
由(4)式可知,任意导弹i在飞行过程中,ζi需要满足如下条件:
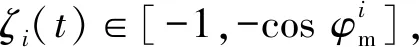
(10)
同时,为实现齐射攻击,由(5)式可知,任意导弹i与导弹j的相关状态需满足(11)式所示的条件:
(11)
基于以上分析,带有不同视场约束的多导弹齐射攻击问题可以转换成状态受限下求取状态一致问题,即根据通信数据,对每枚导弹设计一种协同一致律ui(t),使得导弹相关变量在(10)式约束下,满足(11)式条件。(8)式给出了导弹过载指令与协同一致律的对应关系,因此导弹上施加的实际过载指令可由(8)式的逆运算获得。
2 协同制导律
2.1 协同一致律设计
定义相关变量一致性误差zi(t),i=1,…,N如下:
(12)
式中:βi(t)>0为时变增益;ζr为各导弹前置角参考值,与比例制导(PNG)法的导航比类似,ζr在导弹发射前已经装定好,并保持不变。ζr必须在各枚导弹导引头FOV约束内进行选取,即参考值的选取需要满足(13)式所示的条件:
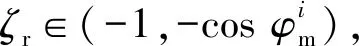
(13)
若无(10)式约束,则各导弹可直接根据一致性误差(12)式设计反馈输入,使得导弹相关状态满足(11)式的条件。文献[8]研究表明,即使是同类导弹,若设置不同的前置角参考值,则不同参考值下的导弹到达目标的时间也不会相同,从而实现对目标的多批次打击。本文为实现多导弹的齐射攻击,为各导弹分配相同的前置角参考值。

由于导弹间以固定周期进行通信,根据(9)式可得导弹i=1,…,N离散采样模型为
(14)
在(10)式约束下,受文献[21]关于多智能体离散模型状态受限下一致性研究的启发,设计一种协同一致律如下:
ui(tk)=PXi(i(tk),zi(tk)),
(15)
式中:PXi(·,·)为饱和函数,
PXi(i(tk),zi(tk))=
i(tk)=i(tk)+zi(tk)h.
本文中各导弹带有不同的视场约束,因此(15)式中的Xi,i=1,…,N互不相同,且各导弹仅知道自身的前置角约束区间,根据自身前置角状态,将一致性误差经饱和函数生成协同一致输入,从而可以确保导弹飞行过程中前置角始终被限制在约束区间内,使目标被锁定在导弹导引头FOV内。
2.2 模型转换
对(14)式进行模型转换,定义如下误差比例系数:
(16)
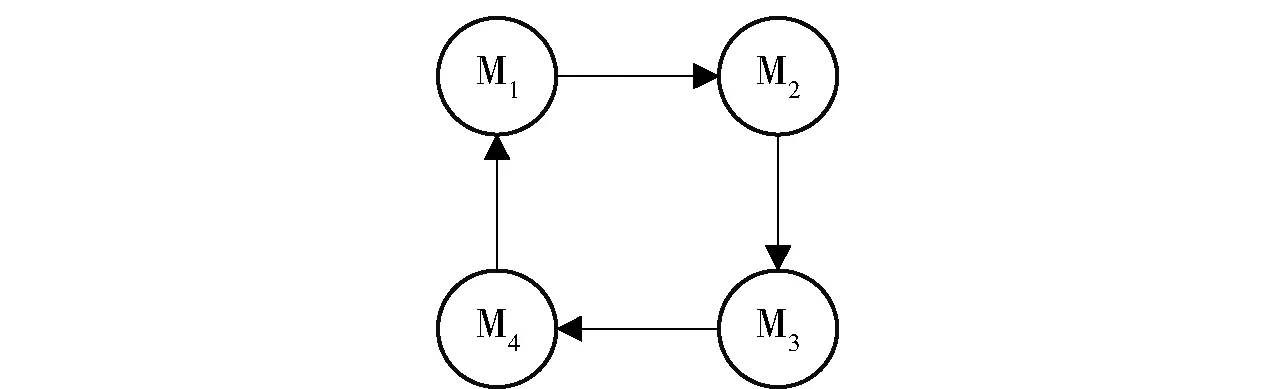
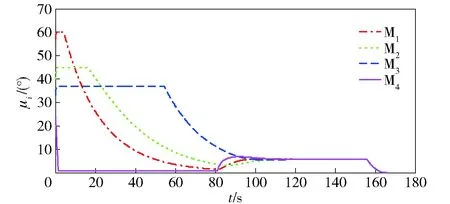
由(15)式可知,0 结合(12)式、(14)式与(16)式,可知 i(tk+1)=ei(tk)i(tk)= (17) 定义临时变量 bi(t)=(1-ei(t)(1-βi(t)h))/h, (18) 可知1-bi(tk)h=ei(tk)(1-βi(tk)h). 结合(17)式与(18)式,可得 i(tk+1)=i(tk)-bi(tk)i(tk)h+ (19) 同时,由(14)式得 i(tk+1)=i(tk)+i(tk)h/2+i(tk+1)h/2. (20) 通过上述步骤,可以将状态约束下的导弹模型((14)式)转换为无状态约束的等效模型((19)式与(20)式),从而可以参考相关多智能体一致性理论实现多导弹协同制导。 由(19)式、(20)式可得 (21) (22) φ(k+1)=(Γ(k)-B(k)(E(k)L⊗I2))φ(k), (23) 令Ψ(k)=Γ(k)-B(k)(E(k)L⊗I2),由(23)式可得 (24) 若(24)式中φ(k)的各分量渐近趋向于同一定值,则(11)式成立。 引理1[22]假设存在一行随机矩阵H∈RN×N,且其对角元素为正。若以H为邻接矩阵的有向图G(H)含有一条有向生成树,则矩阵H为SIA矩阵。 对(24)式进行分析,可得引理3。引理3将有助于证明(15)式给出的协同一致律能使各导弹相关变量满足(11)式条件。 证明当0<βi(t0)h<1时,由(18)式可知,0 当选取βi(tk+1)=bi(tk)时,对于任意k=0,1,…,有 0<βi(tk)≤bi(tk)≤βi(tk+1)<1/h. (25) (26) 由于 (27) 结合(26)式与(27)式可知: 此外,显然有ci(k)>h2lii/2. (28) 当协同制导初始阶段各导弹前置角处于约束区间内时,由协同一致律中饱和函数定义可知,各导弹在其整个飞行过程中前置角均始终处于约束区间内,从而保证了对目标的锁定。证毕。 定理1给出了多导弹实现协同制导的充分条件,并给出了相关参数的选取依据。现有基于多智能体理论所设计的协同制导律一般要求,各导弹协同律具有相同的固定增益,且增益的选取依赖于通信拓扑的全局信息[8-9]。由(12)式可知,本文所提方法中增益βi(t),i=1,…,N并非一致,且独立自适应变化。对于任一导弹i,相关增益的选取只依据通信间隔以及导弹节点的入度信息lii,并不需要知道通信拓扑的全局信息,即本文中各导弹仅依据局部信息自主选择各自协同一致律中的增益。因此,所提协同制导律更适用于异类导弹,特别是多平台发射的异类多导弹协同制导。此外,与现有采用反馈线性化方法所设计的协同制导律相比,本文所提协同制导方法中各导弹的增益βi(t),i=1,…,N在选取时不需要考虑导弹的初始状态,以使得反馈线性化始终有效。 定理1并不要求各导弹的FOV约束相同,且各导弹仅需知道自身的FOV约束,与要求各导弹具有相同FOV约束的相关研究[16-17]相比,本文所提协同制导律更具一般性。此外,现有多导弹协同制导研究大多基于连续时间模型[7-8,15,17],这些制导策略在实际工程应用时依赖于高频的信息交互,以逼近理论上协同的效果,这种高频的信息交互极大地增加了通信网络的负担。本文以采样数据进行协同制导律设计,所有理论分析均是基于周期性通信,因此在实际应用时不需要通过高频通信来逼近理论上的协同效果,从而可以适当放宽对通信频率的要求。因此,本文所提协同制导策略能够有效地降低通信网络负担。 由(8)式可得 (29) 为实现相关变量状态一致,(15)式给出了各导弹的协同一致输入ui(t),因此,由(15)式和(29)式可得协同制导阶段实际施加在导弹i上的过载指令。 为实现静默攻击并减小通信干扰对协同制导的影响,当实现相关变量状态一致且充分接近目标后,各导弹断开通信连接,此时各导弹采用PNG法独立导引至目标,导弹i上施加的过载指令如(30)式所示: (30) 式中:kn∈[3,6]为比例系数常数,kn在各导弹发射前就已装定好,且发射后无法更改。 在实际应用中,各导弹根据网络交互信息实时计算一致性误差((12)式)。当一致性误差收敛至零值附近的极小区域时,认定导弹相关变量状态一致。 考虑由M1、M2、M3、M44枚异类导弹组成的多导弹系统对目标进行齐射攻击,目标位于坐标原点。其中,M1最大视场角为60°,M2最大视场角为45°,M3最大视场角为37°,M4最大视场角为25°. 协同初始阶段各导弹状态如表1所示。由表1可知,协同初始阶段目标处于各枚导弹的视场范围内。根据(13)式以及相关工程经验,选取ζr=-0.995. 表1 导弹初始状态表 若导弹之间无信息交互,各导弹采取PNG法独立导引至目标,则各导弹弹目距离的变化如图3所示。由图3可见,各导弹到达目标的时间不同,且相差较大。因此,各导弹需要根据通信交互数据协同制导,以确保遭遇时间一致。 图3 PNG导引律下导弹弹目距离Fig.3 Range between missile and target under PNG law 当t∈[0 s,156 s)时,各导弹通过通信网络交互剩余距离实现协同制导。导弹间通信拓扑如图4所示,其中箭头表示信息传输的方向。由图4可知,通信拓扑存在一条有向生成树,且各节点的入度为1. 通信间隔h=0.1 s,不失一般性,选取导弹i(i=1,2,3,4)一致性误差增益初始值为βi(t0)=2.1,并根据定理1,选择βi(tk+1)=bi(tk),k=0,1,2,…. 协同制导阶段各导弹过载指令由(29)式可得;当t≥156 s时,各导弹断开通信连接,采用PNG法独立导引至目标,导弹过载指令由(30)式求得,(30)式中取kn=3. 仿真中各导弹最大过载限制为8g,g为重力加速度。 图4 导弹间通信拓扑Fig.4 Communication topology of multiple missiles 仿真结果如图5~图9所示。图5为协同制导阶段相关变量变化示意图。图5(a)表明各枚导弹协调变量ξi(t)状态渐近一致,即各导弹的归一化剩余距离渐近一致;图5(b)表明各导弹前置角渐近收敛于参考值。此阶段内各导弹相关变量达到渐近一致状态。 图5 协同制导阶段相关变量变化示意图Fig.5 Evolution of variables during the cooperative guidance 图6显示了飞行过程中各导弹弹目距离的变化。由图6可知,4枚导弹同时到达了目标,到达目标时刻约为165.5 s,多导弹系统实现了对目标的齐射攻击。结合图5和图6可知,各导弹断开通信连接独立导引至目标并不会影响协同制导阶段的结果。 图6 导弹弹目距离Fig.6 Range among missiles and target 图7显示了在飞行过程中,各导弹前置角的变化曲线。图8给出了制导过程中各导弹上施加的过载指令。由图7可知,各导弹被严格限制在各自FOV范围内,其中,导弹M1、M2与M3在协同制导阶段均有前置角处于各自约束区间边界的现象,表明目标正处于相关导弹的FOV边界。这是因为相应导弹的遭遇时间相对它们的邻居导弹较小,弹道被弯曲。当目标处于导弹FOV边界时,由于FOV约束的存在,弹道无法被进一步弯曲,否则导弹将失去对目标的锁定,因此此时施加在导弹上的过载为0g. 在协调过程中,导弹前置角将收敛至参考值,导弹M1、M2与M3会将目标由其FOV边界拉至范围内,因此施加在弹上的过载指令出现较小的跳变,如图8所示。 图7 前置角变化示意图Fig.7 Evolution of leading angle 图8 过载指令Fig.8 Overload commands 图9为导弹的飞行轨迹示意图。由图9可见,各导弹的弹道相对平直、弹道特性良好。图9中,在协同制导开始阶段,导弹M1、M2与M3弹道均有一定弯曲,而遭遇时间相对邻居导弹较大的导弹M4,其弹道被拉直。 图9 导弹飞行轨迹Fig.9 Missile trajectories 本文考虑二维纵向平面的协同制导制导问题,所得结果同样适用于横侧向平面的导引,因此可将导弹在二维纵向平面与横侧向平面的导引耦合,以得到导弹在三维空间的导引结果。若协同初始时各导弹处于非同一纵向平面内,则三维空间内多导弹也能实现对目标的协同制导,导弹飞行轨迹如图10所示。 图10 三维空间导弹飞行轨迹Fig.10 Missile trajectories in three-dimensional space 本文研究了异类导弹的齐射攻击问题,在考虑各导弹存在不同FOV约束且各导弹仅知道自身FOV范围的条件下,提出一种分布式协同制导策略。所提制导策略能够满足多导弹各自不同的FOV约束条件,且仅需以固定周期交互剩余距离信息,通信量较少,网络负担较小。此外,各导弹协同一致律中的相关增益可独立选取,且各增益的选取仅依据对应导弹节点的入度信息与通信间隔,而无需通信拓扑的全局信息,所提协同制导策略更加符合分布式制导的要求。理论分析与仿真验证均表明,多导弹系统能够实现对目标的齐射攻击,飞行过程中各导弹能始终保证导引头对目标的锁定。 在各导弹带有不同FOV约束的条件下,确保各导弹的相关变量在有限时间内收敛,以及研究通信干扰对导弹协同作战性能的影响,是未来研究工作的重点。本文假设导弹速度恒定,而研究导弹速度变化下的相关协同制导律也具有重要的意义。
ei(tk)[i(tk)-βi(tk)i(tk)h]+
j(t)-i(t))h.
j(t)-i(t))h.2.3 收敛分析


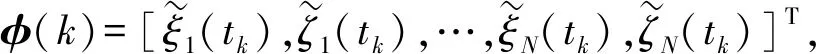


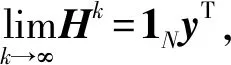




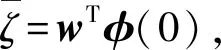
2.4 法向过载
3 仿真






4 结论
