基于近似模型的电动汽车前风窗玻璃除霜性能优化
2019-04-16崔行振王建春管德永
李 旭,崔行振,王建春,管德永
(山东科技大学 交通学院, 山东 青岛 266590)
汽车前风窗玻璃的除霜性能是国家标准规定的强制检测的内容。对于电动汽车而言,良好的除霜性能可节省电池电量,增加续航里程。在新能源车型开发的初始阶段,运用CFD方法进行模拟分析能够节省试验成本,具有重要的实际意义。
国内外的学者对汽车除霜性能改进做了很多研究。谷正气等[1]运用动网格技术研究了出风口的导流叶片,让除霜气流随时间规律变化,先除尽对驾驶员视野的关键区域,进而达到快速除霜目的。HUANG等[2]采用试验与仿真相结合,对风道的内部结构进行优化,使其除霜性能达到要求。葛吉伟[3]综合考虑进风的流量、温度、除霜格栅角度等对除霜特性的影响,获得设计参数对除霜特性的影响规律,得到较佳的除霜效果方案。Patidar Ashok[4]在Fluent中运用能量方程和等温流场进行除霜模拟分析。ROY等[5]搭建实车简易除霜模型,将仿真分析结果与实验结果相比,所得的误差较小,以此验证RNGk-ε湍流模型适合汽车的除霜仿真计算。Alhajri M等[6]综合考虑乘员热舒适性和除霜进气气流的流量、温度等,在满足乘员舱乘客热舒适性的前提下,得到较为理想的除霜通风模式。但是,上述研究多针对传统燃油车型进行研究,针对小型电动汽车除霜性能的研究较少。电池电量作为电动汽车的唯一动力源,对汽车的续航里程具有重要影响,本文研究电动汽车的除霜性能并进行改进研究。
本文的研究对象为某款小型电动汽车。因为除霜出风格栅的偏转角度会在一定程度上改变除霜气流的冲击角以及气流的分布,故本文将添加的两组不同布置方向的格栅的偏转角度作为设计变量,把分割的关键视野区域的近壁面流速作为优化目标,改善该车型前挡风玻璃的近壁面流速分布,以此达到提升除霜效率的目的。
1 原模型的分析计算
1.1 物理模型
本文的研究对象为某款小型电动汽车,包含除霜风道、玻璃、乘员舱等结构,主要研究前风窗玻璃的除霜性能。依据GB11555—2009将前挡风玻璃划分为视野A区、A′区、B区,如图1所示。

图1 玻璃分区示意图
1.2 除霜数学模型
除霜的计算过程分为两个步骤,第1步先经过CFD分析计算得到汽车乘员舱内的稳态流场,第2步再基于此稳态流场作为瞬态计算的初态流场。瞬态分析计算所用的算法是:当热风吹至前风窗玻璃时,先进行对流换热,玻璃将热能传导至霜层,一旦玻璃与霜层的边界上累计的热流超过了霜层的初始能量,霜层就会融化。
霜层的初始能量的计算公式为
Einitial=ρi·t·A(cp·T+L)
(1)
式中:Einitial为初始能量;ρi为霜层密度;t为霜层厚度;A为边界面积;cp为霜层比热;T为温度;L为潜热。
累计边界热流为
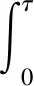
(2)
式中:cemp为经验系数;A为边界面积;qw(τ)为单位面积边界热流。
霜层开始融化后,其剩余霜层的厚度为
S=t·[1-(qloss/Einitial)]
(3)
式中:t为霜层厚度;qloss为累计边界热流[7]。
1.3 网格划分及边界条件设置
本文所用的物理模型在前处理软件Hypermesh 14.0中划分表面三角形网格,在STAR-CCM+中生成体网格。其中,前挡风玻璃采用棱柱体网格离散,乘客舱内部空气域采用四面体网格。拉伸前挡风玻璃和侧窗玻璃,共3层,前挡风玻璃厚度为4.7 mm,增长比为3.5,侧窗玻璃厚度为3.5 mm,拉伸率为2.0。乘客舱边界层厚度为3 mm,层数为2层,拉伸率为1.2,体网格数量为238万。乘员舱及前风窗玻璃处网格模型如图2所示。

图2 乘员舱及前风窗玻璃处网格模型
假定空气为不可压缩气体,常密度,湍流模型为Realizablek-ε模型,空间离散采用2阶迎风差分格式,迭代方式选取Simple算法[8]。边界条件设置如下:除霜风道入口为速度入口,为6.2 m/s, 乘员舱出口为压力出口,乘员舱、仪表板等为绝热壁面边界,玻璃外层设置为对流换热。
1.4 原模型的分析计算
稳态计算的边界条件设置完毕后,首先对该款车型进行稳态分析,得到该车型前风窗玻璃的近壁面速度分布云图,如图3所示。由图3分析可得:视野A、A′区视野中部流速较低,需要进行改进,并进行除霜瞬态分析。
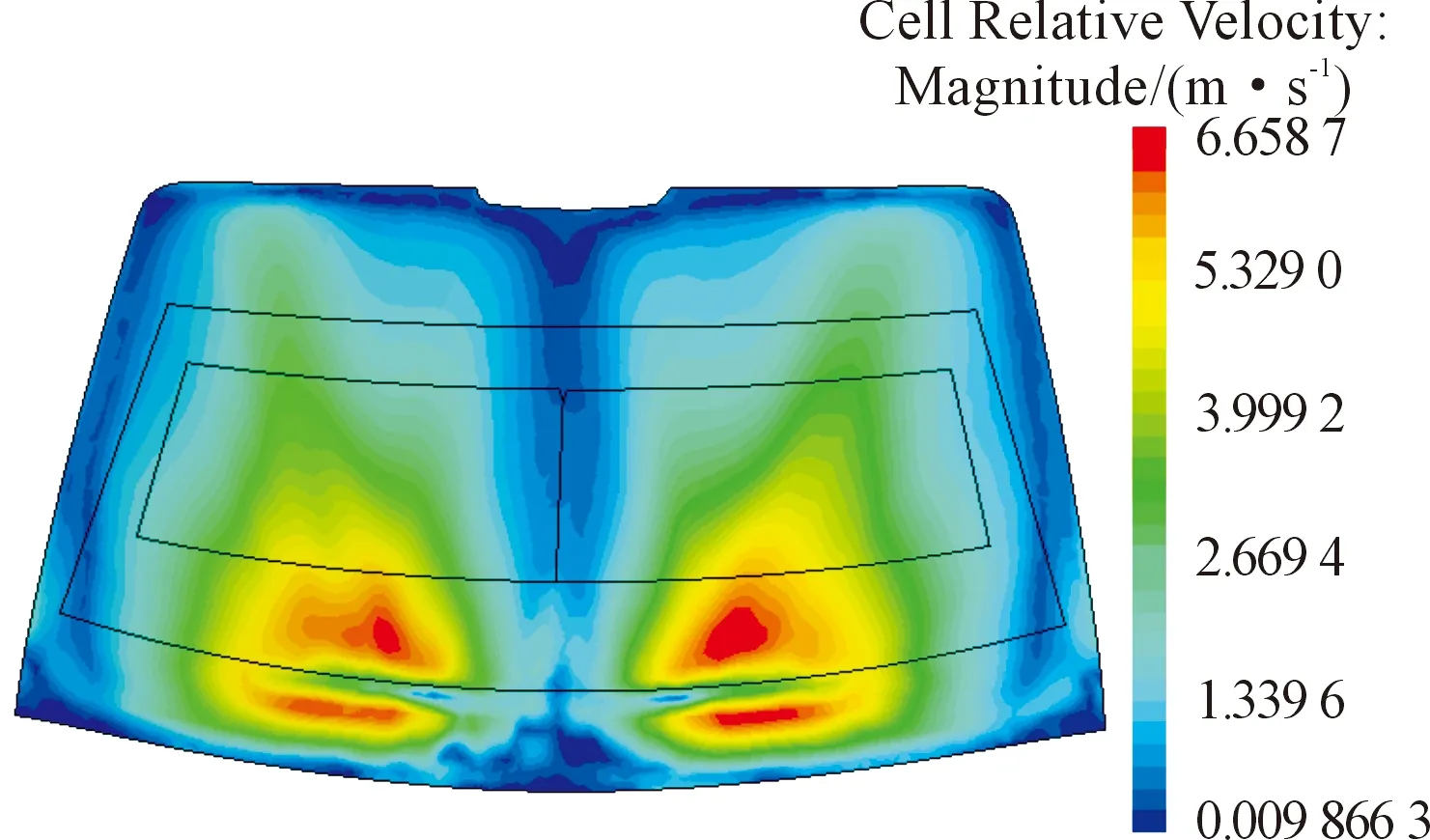
图3 气流速度分布云图
瞬态分析时,试验要求在(-18±3)℃下进行。本文设置外界环境温度为-18 ℃,计算2 400 s,步进1 s,每步迭代5次,霜层的厚度设置为0.5 mm,进风温度按HVAC加热曲线引入,如图4所示。瞬态分析时,空气的动力黏度和热导率在STAR CCM+里通过场函数进行给定。其中T为进气温度,单位为K。场函数如表1所示。
稳态计算完毕后,进行除霜瞬态计算,图5为瞬态计算的不同时刻对应的前挡风玻璃融霜图。将分析结果与国标[9]进行对比,如表2所示。结合图表可知:在25 min时,A、A′、B区均已达到国家要求的除霜标准,因此不再进行后续计算。但在20 min时,A区的除霜比例未达到国家标准,因此需要对原模型进行改进。
表1 场函数

参数函数公式动力黏度U=45e-9×(T-273.15)+1.74e-5热导率λ=82.5e-6×(T-273.15)+0.0243

图4 HVAC温升曲线
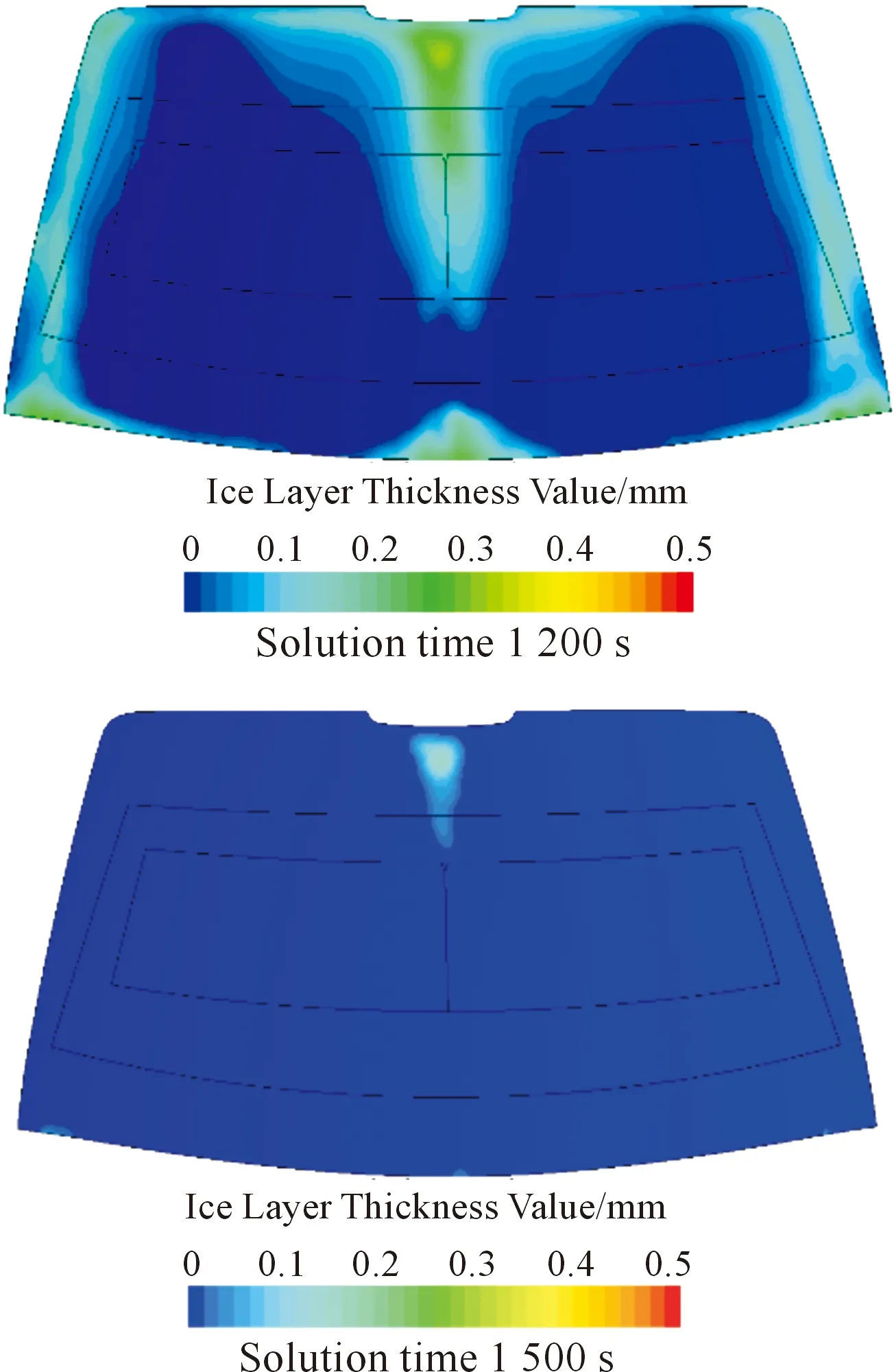
图5 不同时刻前风窗玻璃融霜图
表2 国家标准与仿真结果对比
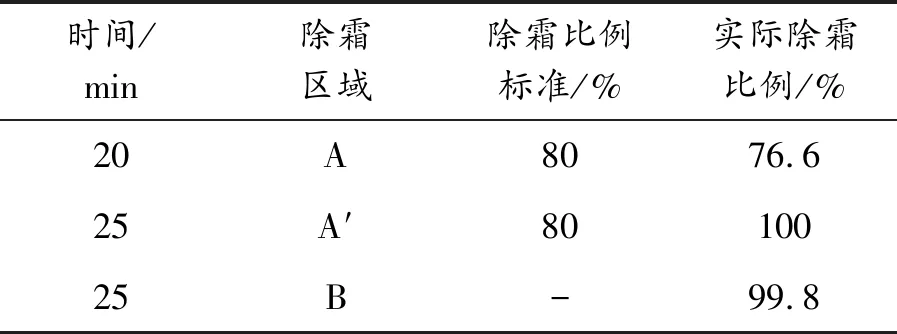
时间/min除霜区域除霜比例标准/%实际除霜比例/%20A8076.625 A′8010025B-99.8
2 优化设计模型的建立
2.1 设计变量的选择
由上面分析可知,视野A、A′区的中部流速较低,所以除霜较慢。由于除霜出风格栅的角度影响风窗玻璃的内表面风速分布,所以合理地布置除霜风道出风口的格栅角度对汽车除霜具有重要的作用。因此,本文添加两种不同布置方向的格栅,并研究其偏转角度对除霜性能的影响。
如图6所示,布置第1、2组不同方向的格栅,1、2组的格栅偏转方向示意图如图6所示。定义1-2组格栅偏转方向为正,其偏转角度为α1;1-1组格栅偏转方向为负,其偏转角度为α2;定义第2组格栅向内偏转方向为正,其偏转角度为α3。
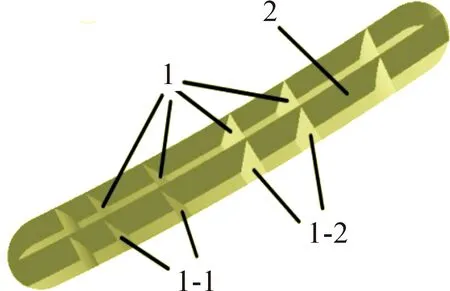
图6 格栅示意图
2.2 目标函数的选择及约束条件的给定
在不改变加热芯体或者PTC热敏电阻加热功率的前提下,汽车除霜的速度取决于玻璃内表面的风速分布,因此前挡风玻璃气流分布应尽可能均匀。稳态分析计算时,在A区、A′区视野区域中部,气流没有覆盖。为使风速的分布更加合理、均匀,在不改变除霜风道大体结构的前提下添加出风格栅,并以偏转角度为设计变量。
由于除霜的出风口采取对称设计,驾驶员的视野区域更为重要,所以选定视野A区的部分区域的近壁面平均流速作为优化目标。将视野A区、A′区分割为以下部分,如图7所示。由上面分析可知,视野A区1部分存在部分低速区且影响部分B区的流速分布,同时为避免第1组中的两种不同偏转方向格栅添加后第4部分区域出现较多的低速区,对第1、4部分配备相等且相对较高的权重;由于第5部分除霜速度较慢,同时第2、5部分能影响气流的分布,故两者配备相同的比重;第6部分优化后速度有所提高,第3部分优化前后高速气流均能覆盖,因此不再研究第3、6部分。因此,优化目标可以简单描述为:
maxV=C1(Va1+Va4)+C2(Va2+Va5)
s.t.α1∈D1,α2∈D2,α3∈D3
式中:Va1、Va5、Va2、Va4分别为A区划分区域第1、5、2、4部分的近壁面平均流速;V为加权后的四部分平均流速和值;C1、C2为权重系数,分别为0.3、0.2;D1、D2、D3分别为α1、α2、α3的设计变量范围,变量范围分别为[0°,45°],[-45°,0°],[0°,25°]。

图7 视野分割区域示意图
2.3 设计变量的试验设计
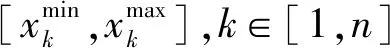
拉丁超立方设计具有有效的空间填充能力和较好的拟合非线性响应,与正交试验相比,拉丁超立方设计用较少的设计样本点数可以表征更多的有效设计空间。此外,拉丁超立方设计对水平值分级宽松,试验次数可以人为控制[12]。因此,本文选用拉丁超立方方法进行抽样,确定选择30组设计样本点,结果如表3所示。
表3 试验设计结果

组号α1α2α310-32.5919.8321.55-23.2820.6933.10-34.142.5944.66-9.3111.21…………3045-24.8318.10
3 近似模型优化结果分析
3.1 建立Kriging近似模型
近似模型(approximate surrogate model)是指能够保持较高的仿真精度,利用插值、回归、拟合等方法构建的计算量小、计算周期短,但是其计算结果与实际仿真结果误差较小的模型。由于克里金插值法构建的近似曲面质量较高,几乎可以覆盖所有的样本点[13],因此本文将通过分析计算得到的30组样本点的数值运用克里金插值法建立近似模型并进行优化。图8为α1、α2关于Va4的近似曲面。
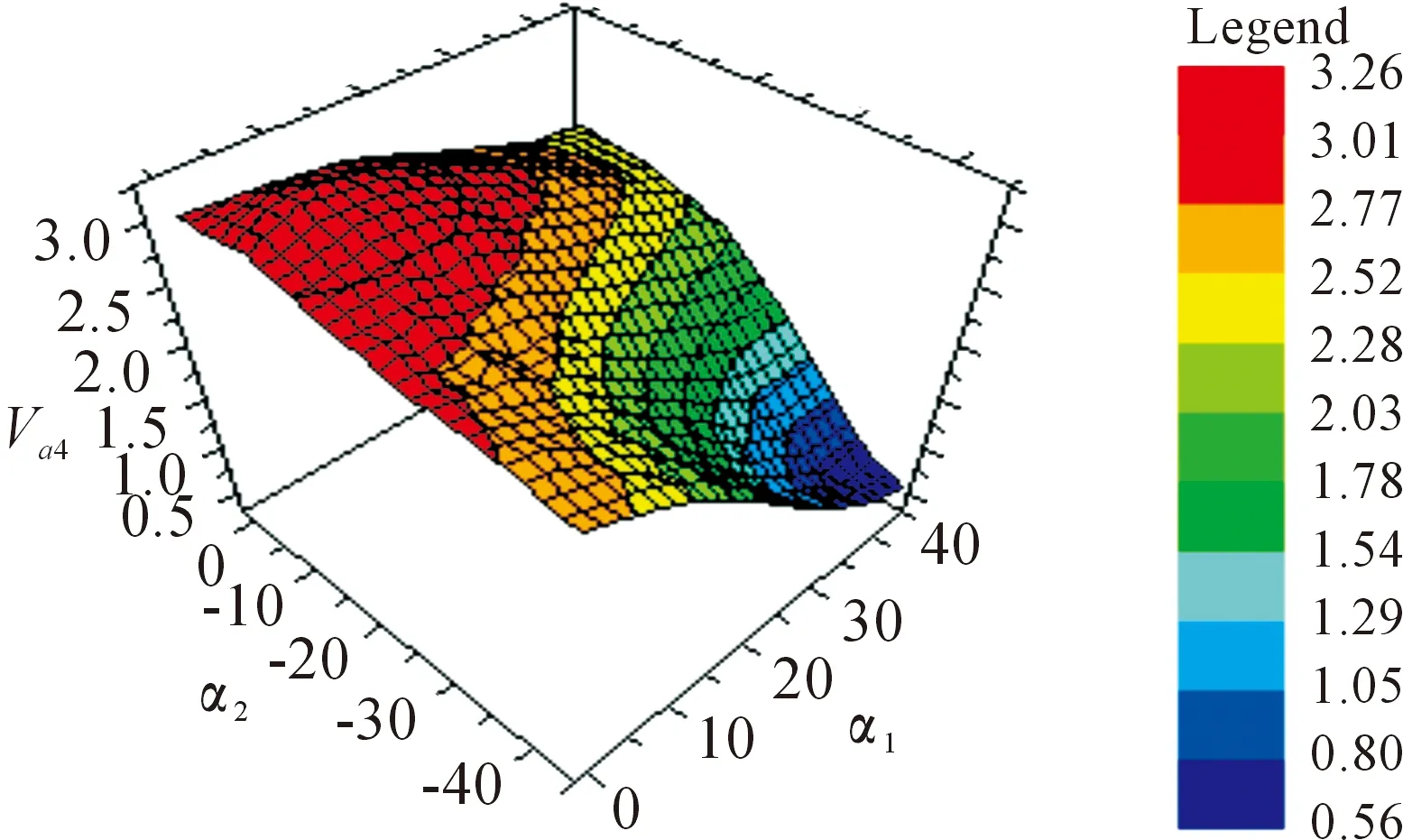
图8 近似曲面
为了检验建立的Kriging模型的模拟精度,需要对其进行误差分析。误差分析主要为4个方面:误差均值、最大值、均方根值及决定系数R2,其中决定系数R2最为重要。前三者的数值越小,说明建立的近似模型误差较小。此外,R2的值应至少在90%以上并接近于1。由表4可知,误差的均值、最大值和均方根基本都在比较小的范围内,决定系数在0.9以上,基本满足工程要求,可知采用该近似模型达到了较高的拟合程度。因此,仿真计算可以用该近似模型代替。
表4 近似模型误差分析
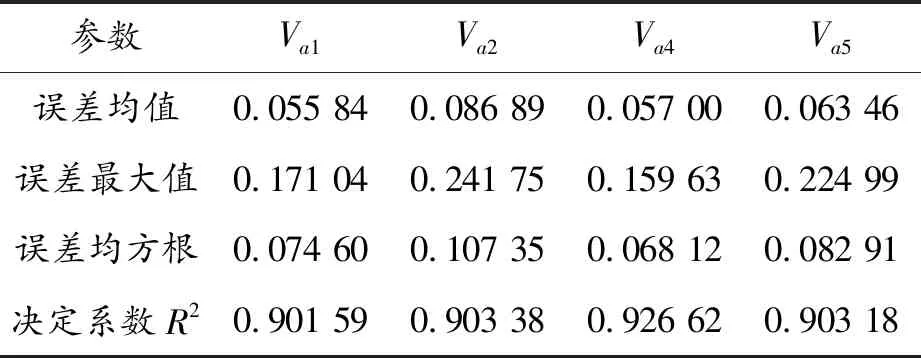
参数Va1Va2Va4Va5误差均值0.055 840.086 890.057 000.063 46误差最大值0.171 040.241 750.159 630.224 99误差均方根0.074 600.107 350.068 120.082 91决定系数R20.901 590.903 380.926 620.903 18
3.2 优化分析
遗传算法是借助自然界生物的遗传和进化过程而发展形成的一种整体的优化算法[14]。多岛遗传算法是在原有的遗传算法基础上形成的一种分群的并行性遗传算法。多岛遗传算法将初始的种群分为多个子群,各个子群分布在不同的“岛屿”,能够单独地进行进化。此外,各个“岛屿”之间可以通过“迁移”在一定时间内进行信息交换。多岛遗传算法具有以下优点:① 能显著地提高运算速度;② 各个子群之间可以完成独立的进化,提高种群的遗传多样性;③ 避免早熟现象,进而寻找最优解[15]。
本文采用多岛遗传算法进行优化,设置种群数量为16,岛屿数为8,迭代代数为50代,最终得到该近似模型的最优解,如表5所示。将优化完的设计变量引入Catia模型中,并对依据最优点设计的模型计算分析,得出仿真值。由表5可知,误差在比较小的范围以内,进一步说明建立的近似模型比较精确,满足要求。将近似模型最优值与依据最优设计点的CFD分析值进行对比,结果如表6所示。
表5 最优点优化结果
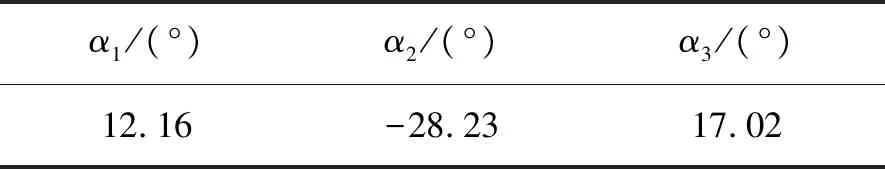
α1/(°)α2/(°)α3/(°)12.16-28.2317.02
图9为优化后该车型前挡风玻璃近壁面的气流速度分布云图。由图10可知,由于格栅的导流作用, A区、A′区视野中部的近壁面平均速度得到大幅提高,低速区死角大幅减小,因此有利于除霜效率的提高。
表6 最优点近似模型值与仿真值对比
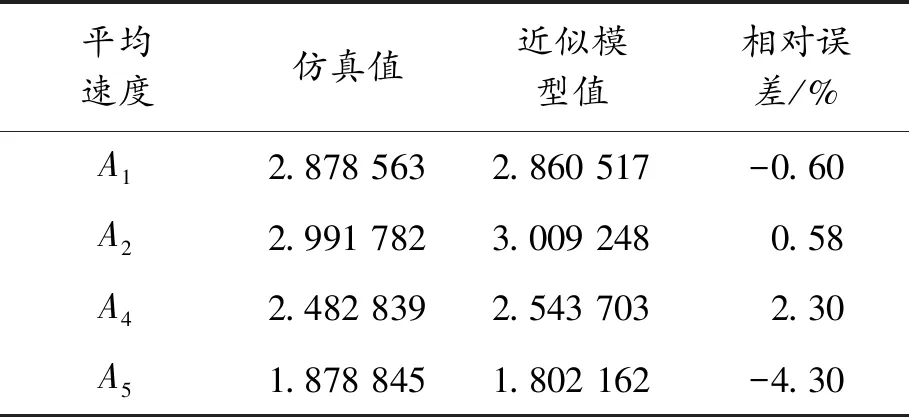
平均速度仿真值近似模型值相对误差/%A12.878 5632.860 517-0.60A22.991 7823.009 2480.58A42.482 8392.543 7032.30A51.878 8451.802 162-4.30

图9 优化后气流速度分布云图
将优化后的模型与初始模型划分的部分视野区域的近壁面平均流速进行对比,如表7所示。对优化前后不分割视野区域的A区、A′区的近壁面平均流速进行对比,结果如表8所示。
表7 优化前后关键分割区域的平均流速对比
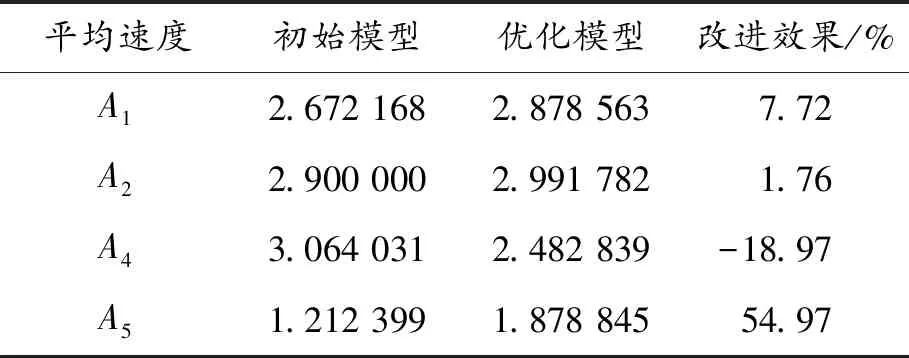
平均速度初始模型优化模型改进效果/%A12.672 1682.878 5637.72A22.900 0002.991 7821.76A43.064 0312.482 839-18.97A51.212 3991.878 84554.97

表8 优化前后A区、A′区平均流速对比
4 除霜效果分析
设置边界条件同前,将优化完成后的模型进行分析计算。在添加的格栅的导流作用下,该车型前挡风玻璃的近壁面速度分布较为均匀。虽然视野A区的第4部分区域的流速降低,但是A区、A′区视野中部的低速死角区域大幅较少,且视野A区、A′区的近壁面平均速度得到提高。
将优化前后20 min和25 min时前挡风玻璃的温度分布云图进行对比,如图10所示。优化后,高温区集中于视野A区与B区之间,而且温度分布更加均匀,满足设计要求。
图11为模型优化后不同时刻的除霜效果图。由图可知,和初始模型相比,在20 min时,优化模型的除霜效果较为显著。除霜比例如表9所示。结合图表可知,通过添加格栅并研究格栅的偏转角度并进行优化设计,可以使该车型的除霜性能满足国标要求。
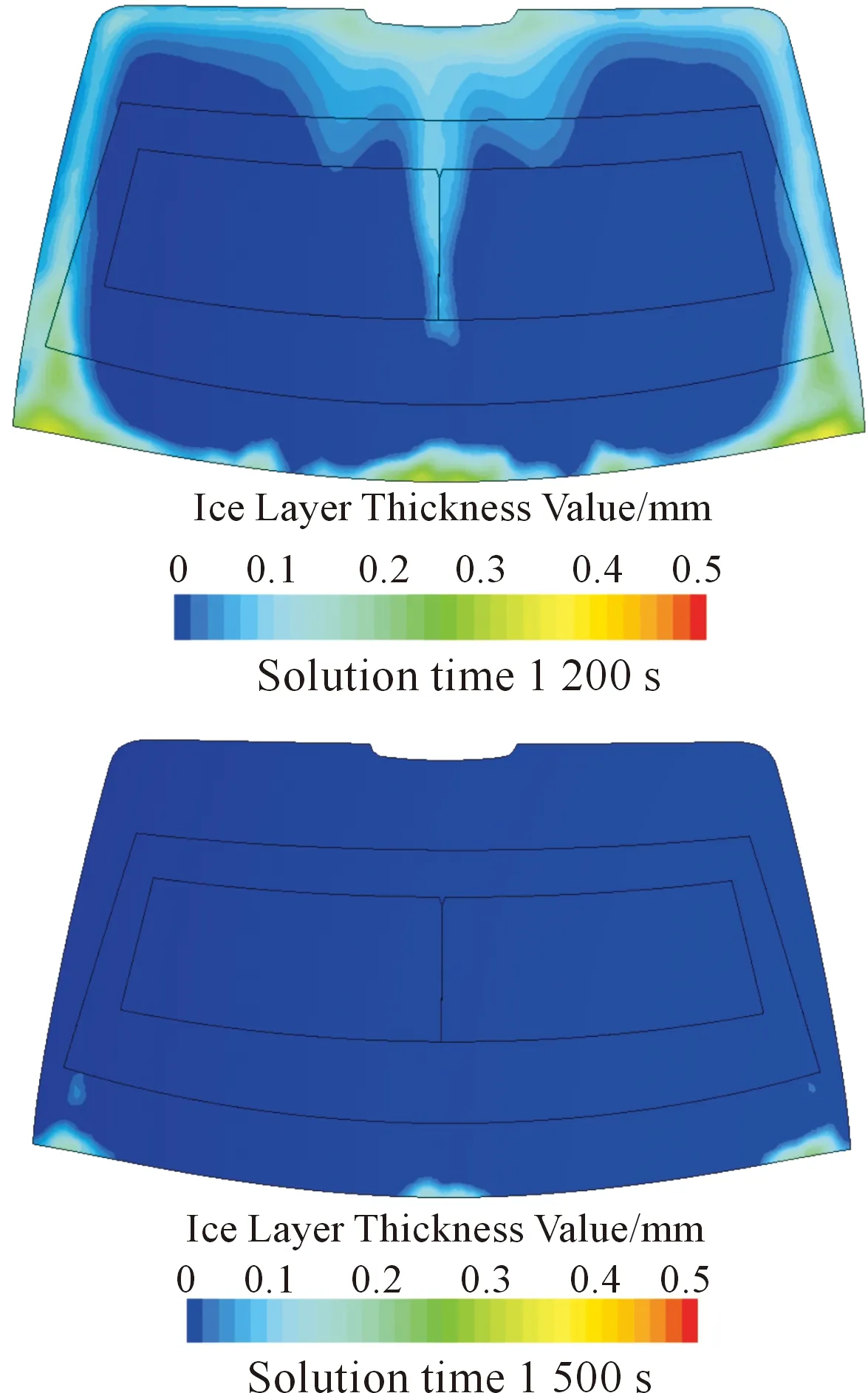
图11 优化后不同时刻的风窗玻璃融霜图
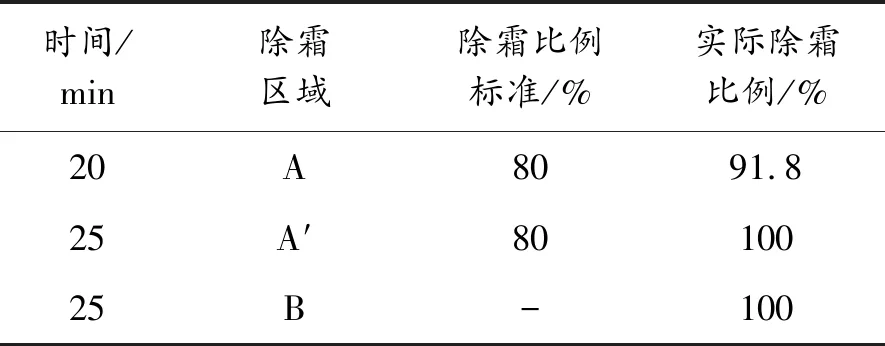
时间/min除霜区域除霜比例标准/%实际除霜比例/%20A8091.825 A′8010025B-100
5 结束语
以某款电动汽车为研究对象,对该车型的除霜出风口进行优化设计。以出风格栅的偏转角度为设计变量,综合考虑两种不同布置方向的格栅,通过拉丁超立方设计拟合得到Kriging近似模型,采用多岛遗传算法进行优化设计。
经过CFD分析发现,优化后视野A区及A′区中部的低速死区大幅减小,优化后A区及A′区的近壁面流速分布均比较均匀,除霜效果得到了改善,满足国标要求。
