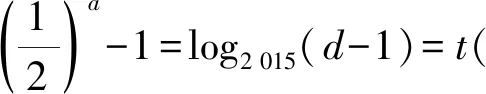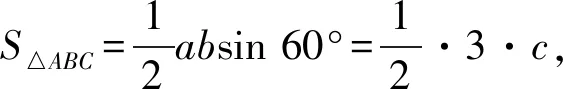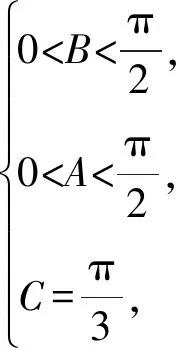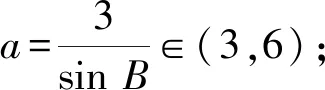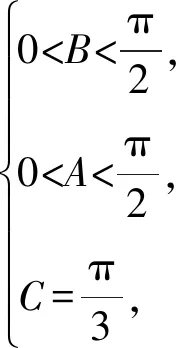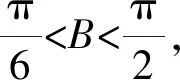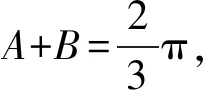“独立变量”的分类解析*
2019-04-15
●
(姜堰第二中学,江苏 泰州 225500)
一般地,若某变量m因另一变量n的变化而变化,则称此变量m为变量n的相关变量[1].相关变量可分为“函数”型相关变量、“方程组”型相关变量、“不等式(组)”型相关变量[2].若某变量m不因另一变量n的变化而变化,则称此变量m为相对于变量n的独立变量,独立变量有哪些情形呢?文章就此做一点思考,整理如下:
1 显性独立变量
若题目给出的两个变量之间具有很明显的独立关系,则可称之为一对显性独立变量.


解依题意,可设A(-1,0),B(1,0),C(cosα,sinα),D(cosβ,sinβ)(其中0≤α≤π,0≤β≤π),则当sinβ≠0,即β≠0且β≠π时,
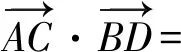
(cosα+1)(cosβ-1)+sinαsinβ=
cosαcosβ-cosα+cosβ+sinαsinβ-1=
sinβsinα+(cosβ-1)cosα+cosβ-1=

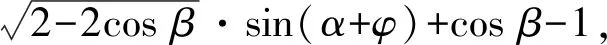
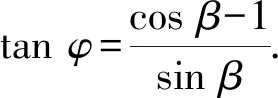
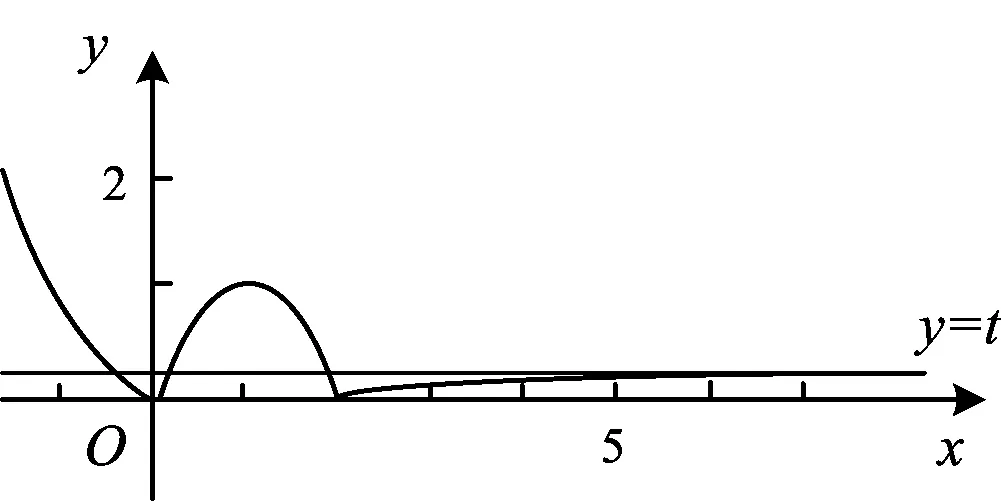
-1 从而 另外,当sinβ=0时,β=0或β=π.当β=π时, -2(cosα+1)∈[-4,0]; 评注这是一道双变量问题,无法通过消元或减元降为一元问题,从而给解题带来了难度.教师的讲解思路是:先设α为常量,β为变量,在以β为主元的假设下进行减元,然后再以α为主元求得最值.这样的讲解充分体现了数学中“动亦是静,静亦是动”的变量观,但学生仍“丈二和尚摸不着头脑”,不能理解.实际上,由于α,β是一对显性独立变量,因此α,β互不干涉,α的动与不动和β无关,这才是对“动静互化的变量观”最好的解释. 分析显然,这里的4个变量a,b,c,d是两两相互独立的显性独立变量,任何两者之间都没有依存关系,难度更大. 解由 得 (a-c)2+(b-d)2≥(m-2)(ac+bd)+mbc, 从而 a2+b2+c2+d2≥m(ac+bc+bd). 显然当ac+bc+bd>0时,m能取到最大值,于是 即 所以 故 评注此题须借助3个基本不等式解题,根据“ac,bc,bd前的系数要一样”这一条件进行了上述拆分.当然,由于a,b,c,d是两两相互独立的显性独立变量,其取值是完全随意的,因此可以根据不同题目的要求进行合理地拆分,以达到解题的目的. 若题目给出的两个变量之间的独立关系不是很明显,则可称之为一对隐性独立变量.在解题时,若能发现并充分利用隐性独立变量,则可大大简化某些试题的解题过程. 分析题中含有动点P(0,m),但要求的是双曲线的离心率,从而动点P(0,m)与离心率应该是一对独立变量,即离心率与点P的位置无关,属解析几何中的“动中有定”问题.为了降低运算的难度,可对变量m适当赋值. 同理可得 设AB的中点为C,则点C的坐标为 由PA=PB,可得PC⊥AB,从而 于是 2a2=3b2, 故 说明有读者可能会说:例3和例4的解法实质上就是常用的特殊化法(或特值法).确实不错,就是特殊化法(或特值法),此解法在解决某些难题中发挥了不小的作用,深得广大师生喜爱,但是为什么能这样用呢?其背后真正的理论依据是什么?可能好多读者只知其一不知其二,其实问题的本质和真正的理论依据就是隐性独立变量. 若题目给出的两个变量之间表面上是独立的,但实质上却是相关的,可称之为一对假性独立变量.由于假性独立变量比较隐蔽,若不能正确理解,则极易导致解题错误,而且很难发现.在解题时,若能发现假性独立变量,则可大大降低此类试题的错误率. 例5已知函数 若a,b,c,d是互不相等的实数,且f(a)=f(b)=f(c)=f(d),则a+b+c+d的取值范围为______. 图1 错解作出函数f(x)的图像(如图1),由于f(a)=f(b)=f(c)=f(d),可做一条直线y=t与f(x)的图像交于4个点.通过图像可得 -1 则 3 评注此题有4个量a,b,c,d,其中由三角函数的对称性可得b+c=2,结合指数、对数函数的单调性可得 -1 由同向不等式的可加性得 3 天衣无缝,可却是错的!问题出在哪? 解法1依题意,可设 则 a+d=-log2(t+1)+2 015t+1. 设 g(t)=-log2(t+1)+2 015t+1,则 从而g(x)在(0,1)上单调递增, 于是g(x)∈(2,2 015),故4 解法2(极限思想)若a=-1,则d=2 016;若a=0,则d=2,从而 2 于是 4 评注前面的错解在得出-1 例6已知在锐角△ABC中,边a,b,c所对应的角分别为A,B,C,∠ACB=60°,CD⊥AB于点D,且CD=3,试求ab的取值范围. 由余弦定理得 c2=a2+b2-2abcos 60°=a2+b2-ab, 从而 即 ab≥12. 评注错解1由基本不等式只能得出最小值,而最大值是无法求出的,另锐角这一条件还没用到,不可能趋向正无穷.错解2把a,b看成两个独立的变量,求出各自的范围后,由同向不等式相乘得到ab的取值范围,而由错解1知道ab的最小值为12,很明显范围变大了. 从而 于是 ab∈[12,18). 高中数学研究最多的是变量,而变量之间的关系错综复杂,令人眼花缭乱,好多师生为之所困.笔者斗胆将变量分为“独立变量”与“相关变量”,再针对“独立变量”与“相关变量”各自进行分类.当然,个人的考虑毕竟肤浅,不够全面,希望感兴趣的读者对此问题进行更深入的研究.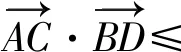
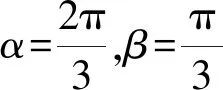
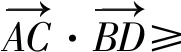
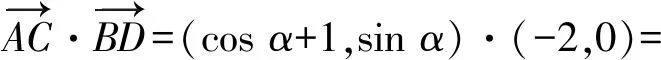
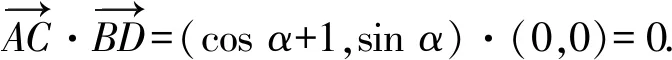

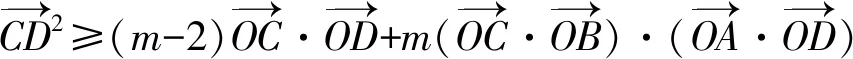

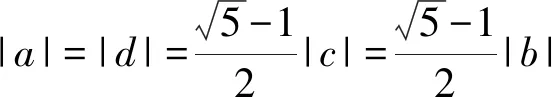
2 隐性独立变量

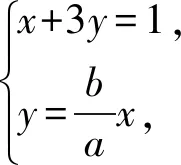
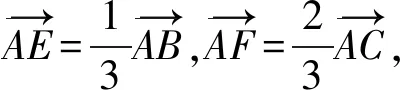
3 假性独立变量