探究多元条件极值问题消元之思维痛点*

●

(柯桥中学，浙江 绍兴 312030)

多元函数条件极值是学生数学学习中的一个“心病”.众所周知，消元需要结构判断与变形技巧，然而“技巧也是知识”，面对多元函数条件极值，准确的审题和正确的解题思路并不意味着题目的解决，还必须正确、专业地完成一些技术性的具体操作：这些工作没有创新性，但需要你的专业性和专注力．现实情况是，对大多数学生而言，这两方面都存在着障碍与思维痛点[1]．

1 思维痛点的主要症状

1．1 多元复杂结构转化不畅

问题1正实数x，y，z满足x+y+z=2，xy+yz+xz=1，则z的最大值是______.

现象一是看不出变量间的关系结构；二是缺少消元思想方法．

事实上，由题意可得

4=x2+y2+z2+2，

即

x2+y2+z2=2.

(1)

又

(z-2)2=x2+y2+2xy≤2(x2+y2)，

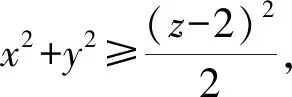
(2)

于是

化简得

3z2-4z≤0，

即

解读条件中蕴含“(x+y+z)2=x2+y2+z2+2(xy+yz+xz)”；建立式(1)与式(2)之间的桥梁是关键．

1.2 多元联系结构识别不畅

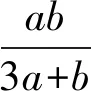
现象看不出条件与目标变量结构之间的联系，解决问题的方法单一．

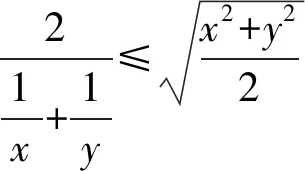
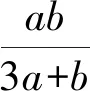
解读在识别出条件与目标之间其实是调和平均与平方平均的关系后，直接利用基本不等式就可以解决问题．

解读只需要两次运用基本不等式就可以破解，但要注意等号成立的条件．

方法3因为

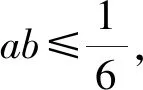
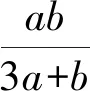
解读在整体思想支配下，把ab视为一个变量去探究目标与条件之间的联系．

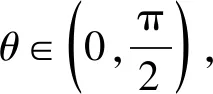
于是

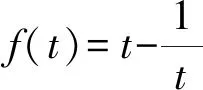
解读将条件二元函数“9a2+b2=1”转化为一元函数最直接的方法就是三角换元．

1.3 消元基本方法运用不畅

现象面对两个量之和为定值1，不会用均值法减元，也不会对目标整体设元．

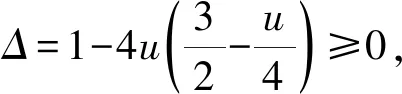
u2-6u+1≥0,

即

从而

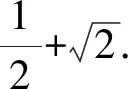
方法2令a+b=t，则b=t-a，代入条件得

2a+4(t-a)+a+2=(a+2)(2t-a),

即

4t-a+2=-a2-2a+2at+4t，

整理得

a2+(1-2t)a+2=0,

从而

Δ=(2t-1)2-8≥0,

即

解读均值消元的前提条件是题设中有两个变量之和为定值，借助于均值法可以化归为一元函数，此时至少有两个途径：一是化成二次方程，然后用判别式法建立目标函数的不等关系式；二是利用导数工具求最值，从而求得二元函数的最值．

2 思维痛点的产生之源

2.1 代数式结构判断意识不强

多元函数条件极值问题的信息中，代数式是基本的，因此代数式结构特征的判断成为解决问题的首要方法.然而，学生在代数式结构判断方面意识不强，从而导致求解失败或受阻，以上各现象都说明这一点.

2．2 多变量消元基本方法不熟

多元函数条件极值的第二个特征就是变量多，要消元.不同结构特征的代数式消元的方法也不同，然而学生针对不同类型的多元结构，消元的基本方法掌握不足、运用不熟，从而导致消元失败或找不到问题求解的基本思路.

2.3 多元极值的基本思想不牢

解决多元极值问题的基本思想方法有：消元意识、消元技巧、变形能力、运算能力，这些是问题突破的基本途径.在脑海中若没有这些基本思想方法，就无法解决此类问题，痛点自然产生．

3 思维痛点的解除之法

3.1 有目标的基本功训练

问题4若实数x,y满足x≥-1，y≥-1且2x+2y=4x+4y，求22x-y+22y-x的最大值．

目标识别条件与目标中的结构特点，呈现问题的本质结构．

事实上，该问题中条件与目标最明显的表征就是指数形式．

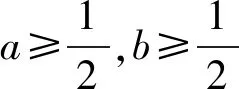
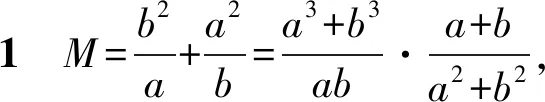
(3)

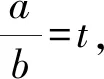
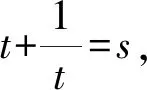
已知式2x+2y=4x+4y可转化为

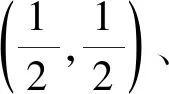
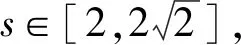
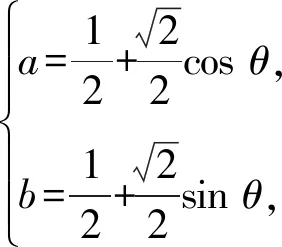
令t=sinθ+cosθ，则

且

2sinθcosθ=t2-1,

从而

3.2 有序思维链接的训练

问题求解过程的有序思维可以进行程序化设计.编制一个程序框图或程序，让学生的思维训练更加有序，思维过程表达更加有序．

问题5设x,y为实数，且x2+2xy+4y2=6，求x2+4y2的取值范围．

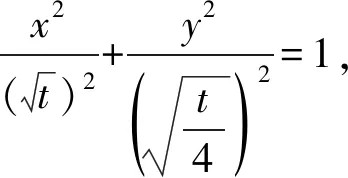
tcos2θ+tsinθcosθ+tsin2θ=6，

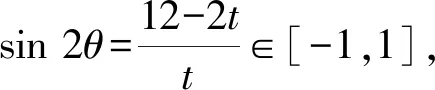
方法3条件配方得

(x+y)2+3y2=6，

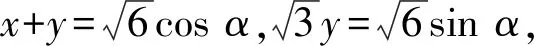
m2-2n=6，x2+4y2=m2-4n,

将x=m-2y代入x2+2yx+4y2=6得

4y2-2my+m2-6=0.

0≤m2≤8，

于是x2+4y2=m2-4n=m2-2(m2-6)∈[4,12].

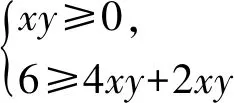
解读对于上述问题的求解训练，针对条件与目标结构进入“挖掘”序列，进而得到相应的“求解方法”序列，这两个序列为子程序，可以再设计，为编制函数条件极值方法挖掘的程序设计打基础．有序思维链接的程序设计是人工智能在数学解题思维链(数学思维基因)研究的基础．

3．3 靶向治疗的专项训练

针对数学学习思维痛点的类型，选择有针对性地“治疗”或解除方法，随着痛点的变化情况，时时调整“校正手段”，以达到有效“诊治”，这种治疗类似于“西医”治疗，快而短期有效，但有副作用，不能保持长期有效或根治．

1)它可能是“点穴式”的，针对某一个“知识点”或“专题”进行“诊断治疗”；

2)它可能是“住院式”的，针对某一块“知识网”或“方法群”进行较长时间的“观察治疗”；

3)它可能是“理疗式”的，针对某一个不良习惯进行“监督”校正．

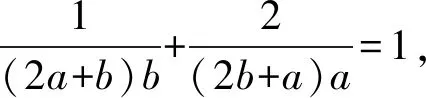
解法1(结构剖析+基本不等式)

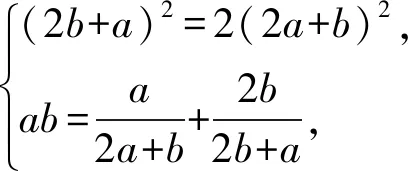
解读目标与条件之间的代数结构联系是关键，第一个等号是容易想到的；第二个等号建立在2a+b,2b+a之间的数量关系上；第3个等号在于化简呈现出对勾函数形式，为使用基本不等式奠定基础；最后在求最大值点时，要解一个复杂的二元分式方程组，这是运算障碍．

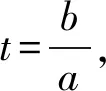
令u=t-1(为求最大值，考虑其大于0)，则

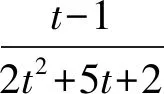
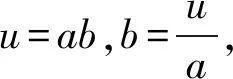
即

(2u+b2)(2u+a2)=6u+a2+2b2,

整理得 (2u-1)a2+(2u-2)b2+5u2-6u=0,

即

(2u-1)a4+(5u2-6u)a2+(2u-2)u2=0.

此方程为关于a2的二次方程，由判别式可得

(5u2-6u)2-4(2u-1)(2u-2)u2≥0，

即

9u2-36u+28≥0,

从而

当且仅当

即

时，取到等号．

解读判别式法相对比较固定、程序化，容易掌握，只是与前所述，在求最大值点时，要解一个复杂的二元分式和二元二次方程组，这是运算障碍．

4 解除思维痛点，积累经验之旅

4.1 善于积累思维方法

教师要引导学生不断积累多元条件极值的各种分析方法，对于多元函数关系结构形式能多角度变形，以挖掘其特征，特别是各类可能情形的全面考虑，意在培养全面思考问题的素养，而不仅仅是线性思考某一个问题；对于多变元条件极值问题，学会分解到基础知识与基本方法层面，然后逐一解决，这也是在培养面对复杂问题、认识问题本质、化整为零、个个击破的素养[2]．

4.2 及时解除思维痛点

及时解除解决有关多变元条件极值问题中遇到的思维痛点：一方面积极地面对多元函数结构变形中的痛点，分析原因，找到产生痛点的根源；另一方面寻找解除痛点的思路与方法，这一过程本身也是在积累求解经验，从而驾驭此类问题[3]．

4.3 勤于总结思维经历

数学学习是有规律可循的，把遇到的若干个痛点归类研究与思考，寻找一些共有的特征，发现其共性，找到一般的思维方法与破解对策，举一反三，融会贯通，做练习时，永远把目的放在心中最重要的位置，变“刷题烂练”为“聚汇精练”，将知识与实践更好地结合，真正提升数学学习的有效性[4]．