数学微专题教学：从“学会”走向“会学”*——以“一类绝对值函数的最值问题”为例

●

(象山县第二中学,浙江 象山 315731)

“微专题”通常是指围绕重点和关键点设计的、利用具有紧密相关性的知识或方法形成的专项研究，或者结合学生的疑点和易错点整合的、能够在短时间内专门解决的问题集.“微专题”教学具有“因微而准、因微而细、因微而深”等特点，能起到“见微知著”，促进学生深度学习的目的[1].

1 问题：微专题教学的出发点

微专题针对的是学生存在的真问题、实问题，因此，在选题时切忌大而空.教师首先要了解学生到底存在着哪些问题、哪些是有价值的、哪些能够串联成合适的知识链，进而形成微专题.

1)当a=0，b=1时，写出函数f(x)的单调区间；

3)若对任意实数a，b，总存在实数x0∈[0，4]使得不等式f(x0)≥m成立，求实数m的取值范围.

(2015年1月浙江省数学学考试题第34题)

1.1 常规解法

1),2)略.

3)解设H(t)=|at2-t+b|，其中t∈[0,2]，则原命题等价于对任意实数a，b,H(t)max≥m.记函数H(t)在[0,2]上的最大值为G(b)，只要G(b)min≥m.

①当a=0时，

G(b)=max{H(0),H(2)}=max{|b|,|b-2|}，

此时，当b=1时，G(b)的最小值为1，故m≤1.

②当a<0时，

G(b)=max{H(0),H(2)}=max{|b|,|b+4a-2|}，

此时

G(b)min=1-2a>1，

故m≤1.

G(b)=max{H(0),H(2)}=max{|b|,|b+4a-2|}；

此时

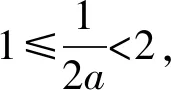
此时

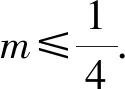
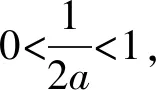
此时

关于函数这部分内容，笔者已经进行了系统复习，各类题型也练习了不少，但学生在类似上述含绝对值的函数最值问题中的得分率还是较低.虽然利用分类讨论和数形结合的数学思想、借助绝对值三角不等式可以解决此类问题，但分类过程过于繁琐，学生“望而生畏”.在近几年的数学高考中，此类问题也是频频作为压轴题出现，是考查的热点之一.因此，探寻此类问题的破解之道就显得非常有价值.

1.2 解法优化

图1

上述思路非常高效地破解了此类问题的思维瓶颈，具有很大的推广价值.此法虽然简洁，但学生理解起来却并不简单，以微专题的形式开展此法的探究教学就显得尤为必要.

2 “学会”：微专题教学的首要任务

确定了微专题的主题，下面就是围绕这个主题，根据学生在学习中遇到的思维障碍，通过精心设计问题与例题来编制对应的微专题.例题与问题的呈现一般遵循从简单到复杂、从特殊到一般的原则，其目的是为了降低学生学习的门槛，通过抽丝剥茧式的逐层剖析，揭示问题的本质，从而使学生“学会”如何解决这一类问题.

2.1 回归思维的起点

数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上.因此，微专题中起始问题的设计不能让学生“望而生畏”，而是要让学生有种“似曾相识”的感觉，“稍微跳一跳就能够得着”.因此，起始问题设计最好能够回归教材，回归到思维的起点.

挖掘母题，发现联系，因为起点往往也是知识的生长点.对于上述微专题，起始问题可以这样设计：

例2函数f(x)=|x-b|,其中x∈[-1,1]，b∈R，记f(x)的最大值为g(b)，则g(b)的最小值为______.

解法1(代数视角)

因为g(b)=max{|1-b|,|-1-b|}，则

从而 2g(b)≥ |1-b|+|-1-b|≥

|1-b-(-1-b)|=2,

于是g(b)≥1,当且仅当1-b=-(-1-b)，即b=0时，等号成立.

图2

解法2(几何视角)

|x-b|的几何意义：如图2，过x轴上一点Q(x,0)(其中x∈[-1,1])作x轴的垂线，交y=b于点M，交y=x于点T，则

|x-b|=|MT|.

当b>0时，|MT|的最大值为|AA′|,显然，当y=b与x轴重合时，|AA′|取得最小值1.同时，当b<0时，|AA′|的最小值也为1.

评注将例2作为例1的引例，该题比较基础，学生容易入手.从代数和几何两个视角对此题进行分析，既有助于学生对此类问题形成整体认知，又可以凸显几何的直观性，为后续的研究指明方向.

2.2 设计问题串

问题是数学思维活动的载体，而课堂的重要构成因素就是问题.孤立的问题对思维发展的作用微乎其微，教师要注重问题串的整体性，在问题串的引领下，让学生进行系列、连续的思维活动，才能让学生的思维达到新的高度.

例3函数f(x)=|x2-2x-b|，其中x∈[-1,1]，b∈R，记f(x)的最大值为M(b)，则M(b)的最小值为______.

分析|x2-2x-b|的几何意义：如图3，过x轴上一点Q作x轴的垂线，交y=2x+b于点M，交y=x2于点T，则|x2-2x-b|=|MT|.观察发现，当直线l位于l1与l2正中间时，M(b)取到最小值，即

图3 图4

例4函数f(x)=|x2-ax-b|，其中x∈[-1,1],b∈R，记f(x)的最大值为M(a,b)，则M(a,b)的最小值为______.

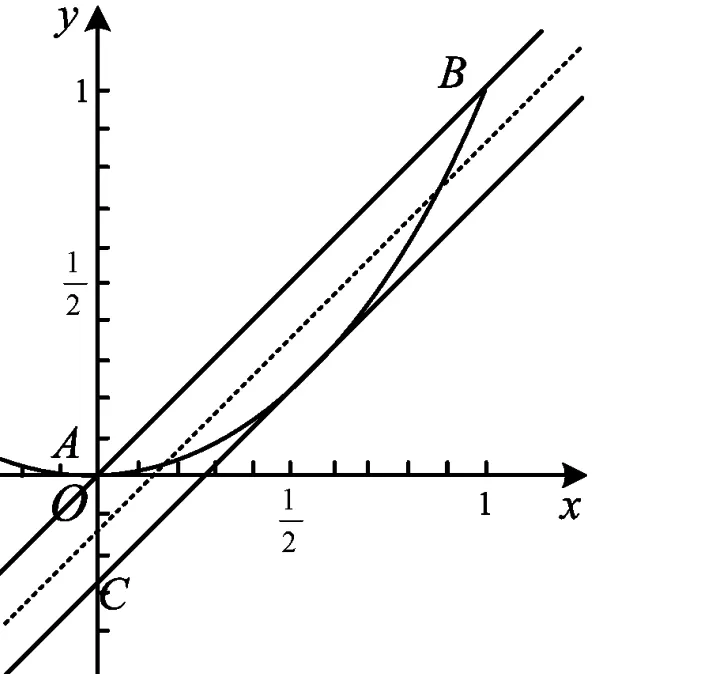
图5

例5函数f(x)=|x2-ax-b|，其中x∈[0,1],b∈R，记f(x)的最大值为M(a,b)，则M(a,b)的最小值为______.

评注通过由易到难的问题变式，将一组问题按照一定的逻辑串题成链，以问题解决代替方法灌输，从而有效地突破教学难点，使得学生的认知逐步深入，达到新的深度.

2.3 获得方法模型

数学方法模型指引着问题解决的道路.数学解题中若缺少对方法模型的掌握，即缺少对“中间环节”的认识，则会与最终目标之间产生难以逾越的障碍.一言概之，解题不是目的，获得方法模型才是微专题教学的主要任务.

经历上述问题的解题过程，可以猜想得到下面的结论：

3 “会学”：微专题教学的终极追求

教师在引领学生“学会”的同时，还需追求学生“会学”的境界，“先生责任不在教，而在教学，教学生学”[2].因此，推动教与学的根本在于教学生学，让学生“会学”，这也是数学微专题教学的终极目标.学生“会学习”的两个层次是“得法”与“得道”[3].

3.1 得应用之法

会学习的学生拥有对知识结构进行组织和再组织的综合迁移能力,善于举一反三、触类旁通、学以致用.因此，在上述微专题教学中还应该加上应用环节，通过设计丰富的问题情境，让学生获得灵活运用结论解决问题的诀窍.

(2017年浙江省数学高考理科试题第17题)

分析此题是研究含绝对值函数的最大值问题.若考虑去绝对值，则原函数可以转化为一个分段函数来讨论，解答过程比较复杂.若能直接利用上述结论，则能很快获得答案.

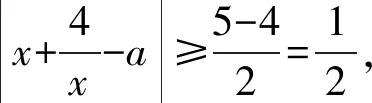
例7设函数f(x)=|x2+a|+|x+b|，当x∈[-2,2]时，记f(x)的最大值为M(a,b)，则M(a,b)的最小值为______.

分析先把两个绝对值化为一个绝对值，就可以直接利用结论解题.

f(x)= |x2+a|+|x+b|≥|x2+a+x+b|=

|x2-(-x-a-b)|,

或f(x)= |x2+a|+|x+b|≥|x2+a-x-b|=

|x2-(x-a+b)|,

然后分别求出两种变形情况下的M(a,b)，最后取交集就可以获得答案.

评注通过上述两道例题的解决，学生不仅能够体会利用现成结论解决问题的“成就感”，而且还会发现“设函数f(x)=|g(x)-ax-b|在闭区间D上的最大值为M(a,b)，求M(a,b)min”这一类问题中的函数不仅可以是一次函数、二次函数等简单函数，还可以对勾函数等复杂函数.也就是说，这个解题方法适用于任意函数.

3.2 得研究之道

会学习的学生，注重结果的知悉，善于诊断、反思自己的学习活动，也倾向于通过反馈、归因的途径提高自我的内驱力.“得道”强调的是善于认知和把握事物的规律，在学习中能够抓住、抓准知识的核心，并弄清其规律，按规律求知、认知.就本微专题而言，学生能够感受到解决这类问题的一般方法，那就是立足几何视角，借助数形结合思想把抽象问题直观化，进而发现问题的实质，采用“以静制动”的策略找到问题的突破口.这种研究问题的“套路”在数学解题中具有广泛的适用性.

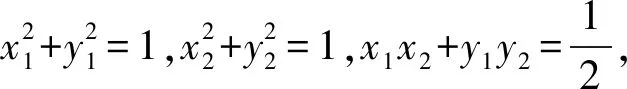
(2018年上海市数学高考试题第12题)

分析此题表面上看是以代数作为命题背景，但其中涉及到4个参数，且这4个参数间存在着3组非线性的关系，无法通过消参来实现简化运算的目的.题目要求的结果是含绝对值的多变量关系式，对于此式的代数化简很难操作，若从几何视角入手就简单得多了.

图6

建立如图6所示的直角坐标系，设A(x1,y1)，B(x2,y2),且点A,B在单位圆上运动，则

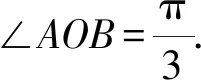
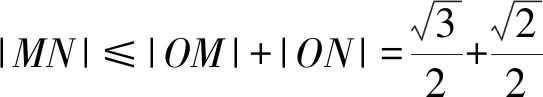
例8可以作为本微专题的“思维拓展”模块中的内容.至此，本微专题的内容框架得到明晰，“问题提出、引例、问题探究、学以致用、思维拓展”等五大模块构成了整个微专题.本微专题的设计既体现出教师“教”的思路，又为学生铺设了“学”的路径，最终帮助学生实现从“学会”向“会学”的飞跃.