一类带组合项的分数阶边值问题两个解的存在性
2019-04-13李姗姗王智勇
李姗姗,王智勇
(南京信息工程大学数学与统计学院,江苏南京 210044)
1 引言
考虑如下分数阶边值问题
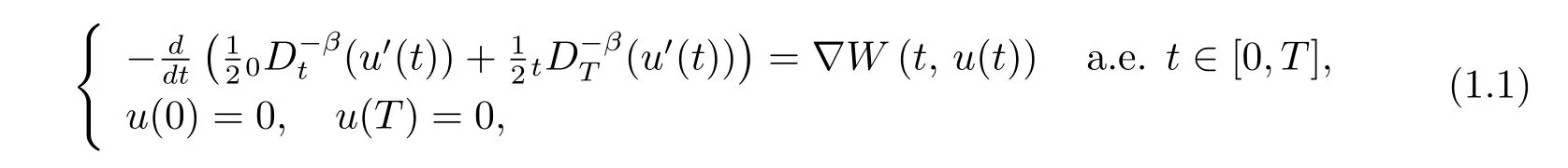
随着分数阶微积分的发展,其已涵盖了科学与工程的很多应用领域,特别是近30年以来,已应用到流体力学,粘弹性力学,反常扩散,分数控制系统,各种电子回路,生物系统的电传导,神经的分数模型等,并且已有了成熟的发展,见文献[1–6].
近年来,许多学者利用各种方法对问题(1.1)进行了研究,并得到了很多重要的结果.2011年,Jiao和Zhou在文献[7]中首次建立了问题(1.1)的变分结构,并利用极小化作用原理以及山路引理得到了问题(1.1)解的存在性;在文献[1]中,陈在位势函数W(t,x)满足渐近二次的条件下,利用山路引理研究了问题(1.1)解的存在性;文献[2]中,陈和唐运用喷泉定理和对偶喷泉定理分别考虑了位势函数W(t,x)为超二次和次二次的情形,得到了问题(1.1)存在无穷多个解.
令
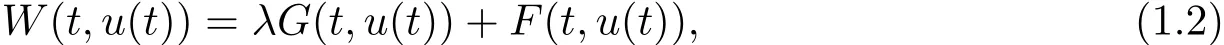
其中λ>0,F(t,u(t))和G(t,u(t))在无穷远处分别是超二次和次二次的.最近,文献[4]首次研究了具有形如(1.2)式这样组合项的位势函数,借助于山路引理和极小化方法得到问题(1.1)至少存在两个非平凡解.受上述结果的启发,本文利用山路引理以及Ekeland变分原理,进一步讨论此类带组合项的问题(1.1)两个解的存在性.我们有
定理1.1 假设W满足如下条件
[F1]∀x∈RN,F(t,x)关于t是可测的,对a.e.t∈[0,T],F(t,x)关于x是连续可微的,且存在a∈C(R+,R+),b∈L1([0,T],R+)使得

其中Γ为通常的伽马函数,α=1−β/2,则存在常数Λ0>0,使得当λ∈(0,Λ0)时,问题(1.1)至少存在两个非平凡解.
注1.1容易看出,这里定理1.1所给的条件同文献[4]相比要更一般,因此结果推广和发展了文献[4]中的结论.
本文结构安排如下:第二部分简要介绍一些分数阶微积分的基本概念并给出本文所需要的预备引理;第三部分给出了定理1.1的证明;最后一部分将给出一个例子来说明结果.
2 预备知识
本节将简要介绍一些分数阶微积分的基本概念,并且给出问题(1.1)的工作空间和变分结构.
定义2.1[8]设γ>0,函数f(t)定义在[a,b]上,它的γ阶左和右Riemann-Liouville分数积分分别定义为
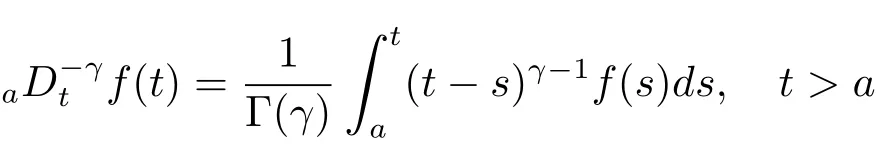
和
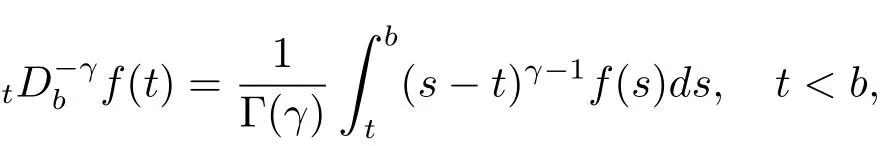
其中右式在[a,b]上逐点有定义.相应的,当γ=n∈N时,上式分别与以下的n次积分形式相对应

和
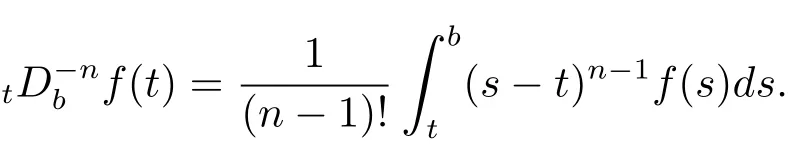
定义2.2[8]设γ>0,函数f(t)定义在[a,b]上,它的γ阶左和右Riemann-Liouville分数导数分别定义为
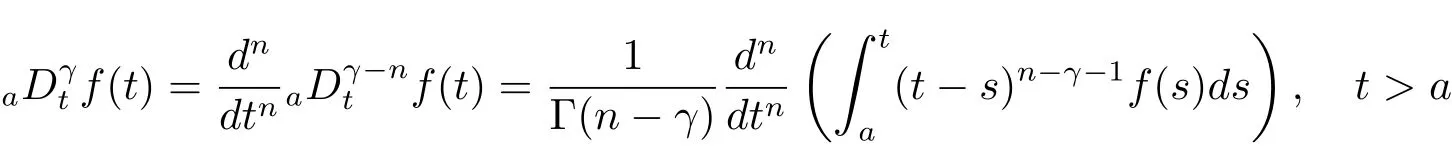
和
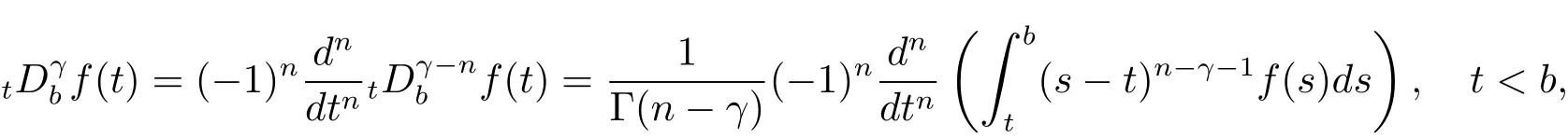
其中t∈[a,b],n−1≤ γ 其中f(n)(t)为f(t)的n阶导数;若0<γ<1,则 和 记AC¡[a,b],RN¢为绝对连续函数空间.对k∈N, 定义 2.3[8]设γ>0,n∈N.若γ∈ [n−1,n)且f(t)∈ACn¡[a,b],RN¢,则函数f(t)的γ阶左和右Caputo分数导数于[a,b]上几乎处处存在,且分别定义为 和 设0<α≤1以及1 其范数为 命题2.4[8]设0<α≤1,1 进一步,若α>1/p且1/p+1/q=1,则有 特别的,当p=2时,有以下两个不等式成立 引理2.5[7]设0<α≤1,1 下面将在空间Eα:=中讨论问题(1.1)的多解性,此时其范数为kukα:=kukα,2. 定义2.6若对u∈Eα以及∀v∈Eα有 则称u为问题(1.1)的弱解. 考虑泛函 根据条件(F1),(G1)和(G3),由文献[7]中的定理4.1可知,ϕ∈C1(Eα,R)且有 引理2.7[7]若1/2<α≤1,则对u∈Eα,有 定义2.8[6]设X是实Banach空间,ϕ∈C1(X,R),如果{un}⊂X,ϕ(un)有界并且ϕ0(un)→0(n→+∞),则称序列{un}⊂X 为ϕ的(PS)序列.如果它的每一(PS)序列都有一收敛子列,则称泛函ϕ满足(PS)条件. 定义2.9[6]设X是实Banach空间,ϕ∈C1(X,R),如果{un}⊂X,ϕ(un)有界并且(1+kunkα)ϕ0(un)→ 0(n→ +∞),则称序列{un}⊂ X为ϕ的(C)序列.如果它的每一(C)序列都有一收敛子列,则称泛函ϕ满足(C)条件. 引理2.10[6](山路引理)设X是实Banach空间,ϕ∈C1(X,R)满足(PS)条件,ϕ(0)=0,且有 (I1) 存在常数ρ,β >0,使得ϕ|∂Bρ≥ β; (I2)存在e∈X¯Bρ,使得ϕ(e)≤0, 注2.2由文献[9]可知,山路引理在(C)条件下依然成立. 为了叙述方便,令Ci(i=1,2,3,···)表示一系列不同的正常数,X=Eα. 引理3.1假设条件(F1),(F5),(F6),(G1)和(G3)成立,则泛函ϕ满足(C)条件. 证 首先证明{un}在X上有界.假设{un}是泛函ϕ的(C)序列,即{ϕ(un)}有界,且当n→+∞时,有kϕ0(un)kX∗(1+kunkα)→0,其中X∗为X 的对偶空间,则∀n∈N,有 根据条件(F5),存在常数R1>0,使得∀|x|≥R1以及a.e.t∈[0,T],有 再结合条件(F1),∀x∈RN和a.e.t∈[0,T],可知 所以利用(2.2)式以及Hölder不等式,可得 而由条件(G1)和(G3),有 因此,进一步依据(2.2),(3.4),(3.5)式和Hölder不等式,可得 这样由(2.4),(2.6),(3.1),(3.3)和(3.6)式可得 另一方面,由条件(F6),存在常数R2>0,使得∀|x|≥R2和a.e.t∈[0,T],有 因此再由条件(F1),∀x∈RN和a.e.t∈[0,T],可得 其中ripi=µ−r+2,1/pi+1/qi=1.考虑(2.4),(2.5),(3.1),(3.4),(3.6),(3.8)和(3.9)式,有 因此可以得到 由于µ>r−1,利用(3.7)和(3.10)式,并注意到εi的定义,有 注意到这里µ>r−1,因此,kunkα有界. 最后证明{un}在X上有强收敛子列.因为{un}在X上有界,并且X是自反的Banach空间(见文献[8]),则存在子序列,不妨仍记为{un},使得在X上,有un*u.于是当n→+∞时,有 由(2.3)式和引理2.5可知{un}在C([0,T],RN)上有界.进一步,当n→ +∞时,有kun−uk∞→0.因此再依据条件(F1)和(G3),当n→+∞时,有 此外,由(2.5),(2.6)和(3.12)式,有 所以结合(3.11)式可得,当n→+∞时,kun−ukα→0,即ϕ满足(C)条件. 引理3.2假设W满足条件(F3),(F5),(G1)和(G3),则存在常数ρ>0,β>0和Λ0>0,使得当kukα= ρ,λ ∈ (0,Λ0)时,有ϕ(u)≥ β. 证 根据条件(F3),(F5)可知,存在常数δ1∈(0,|cos(πα)|),∀x∈RN和a.e.t∈[0,T],有 由(2.1),(2.4),(2.6),(3.13)式及条件(G1),(G3),有 设 因为1 利用(3.14)和(3.15)式可得,存在不依赖于λ的常数C12,使得 引理3.3 假设W满足条件(F1),(F4),(G1)和(G3),则存在e∈X,并且kekα>ρ,使得ϕ(e)<0. 证 由条件(F4)知,存在常数δ2>0和R3>0,使得∀|x|≥R3以及 a.e.t∈[0,T],有 再由条件(F1),∀x∈RN和a.e.t∈[0,T],有 根据(2.4),(2.6),(3.5),(3.16)和(3.17)式,注意到1 所以存在充分大的s0使得ϕ(s0u0)<0,取e=s0u0∈X,有ϕ(e)<0. 引理3.4假设条件(F2)和(G2)成立,则 其中ρ由引理3.2给出. 下证存在ϕ(u0)=h<0. 由条件(F2)知,存在常数δ3>0,使得∀|x|≤δ3以及a.e.t∈[0,T],有 由条件(G2)得,存在常数δ4>0,∀|x|≤δ和有 因此有−∞ 定理1.1的证明 根据引理3.1可知ϕ满足(C)条件,由条件(F3)和(G1)知W(t,0)=0,所以有ϕ(0)=0,再利用引理3.2和引理3.3可知引理2.9(山路引理)中的条件(I1),(I2)成立.因此问题(1.1)存在一个非平凡解u1∈X,使得ϕ(u1)=c>0.另一方面,由引理3.4和Ekeland变分原理(见文献[6]),类似于文献[10]中定理2.1的证明,可得有界的(PS)序列{un},即ϕ(un)有界,且当n→+∞时,ϕ0(un)→0.又因为un∈¯Bρ,即kunkα<ρ,所以当n→ +∞时,有(1+kunkα)ϕ0(un)α→ 0,即{un}为ϕ中有界的(C)序列,再结合引理3.1,则问题(1.1)存在另一个非平凡解u2∈X,使得ϕ(u2)<0.综上所述,问题(1.1)至少存在两个非平凡解u1,u2∈X,使得ϕ(u2)<0<ϕ(u1). 在本节中,给出一个具体的例子来说明我们的结果.考虑如下分数阶边值问题: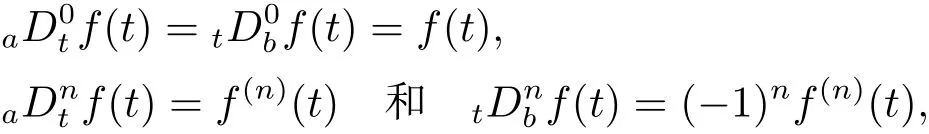
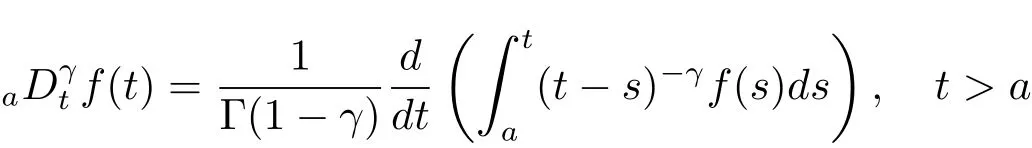
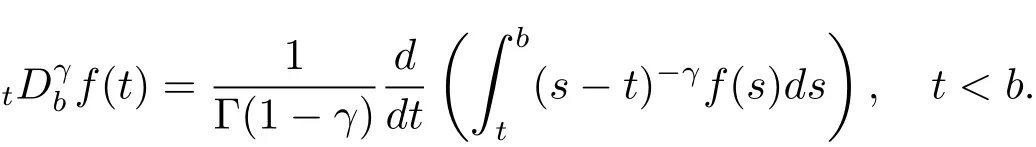
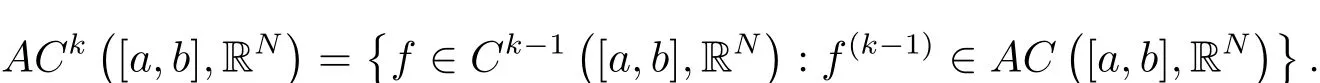
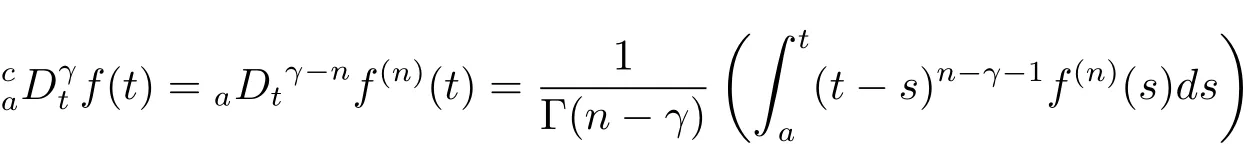
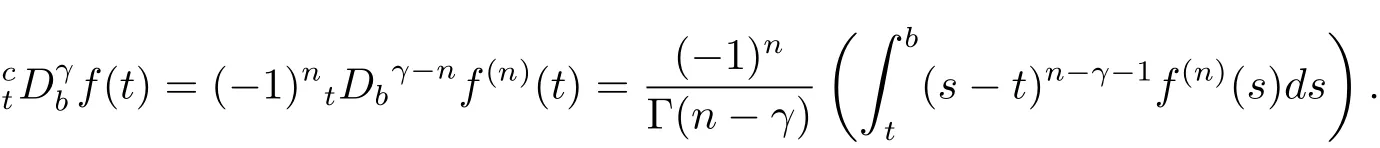
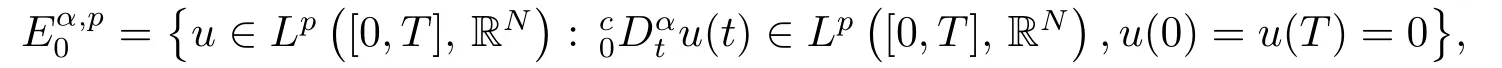
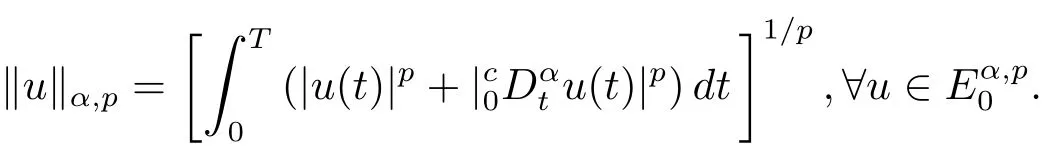



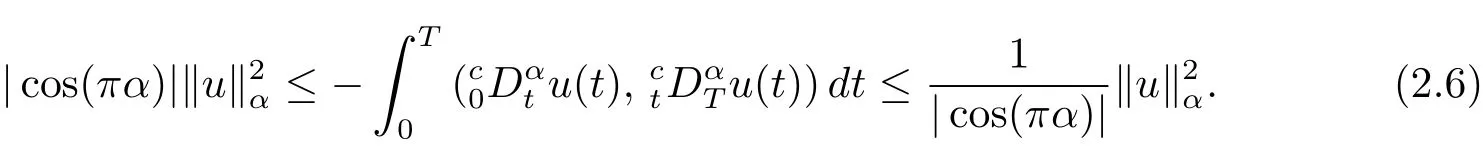
3 定理的证明
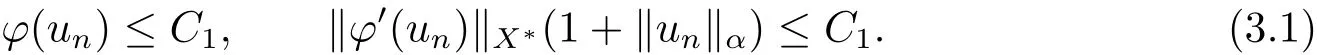


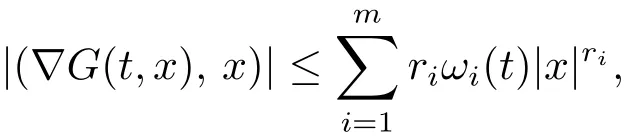
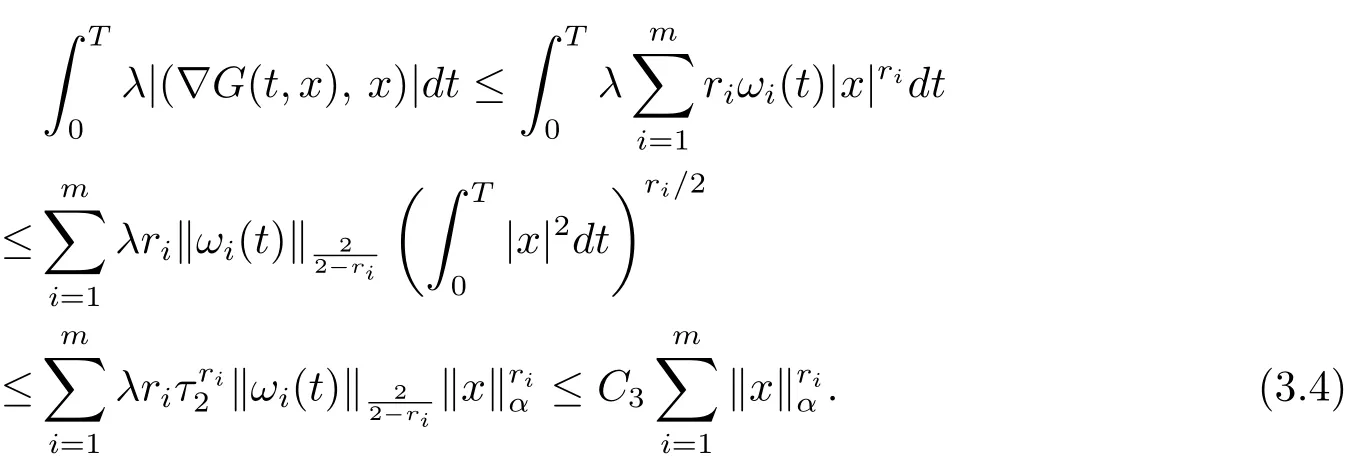
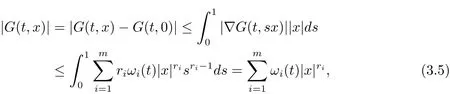
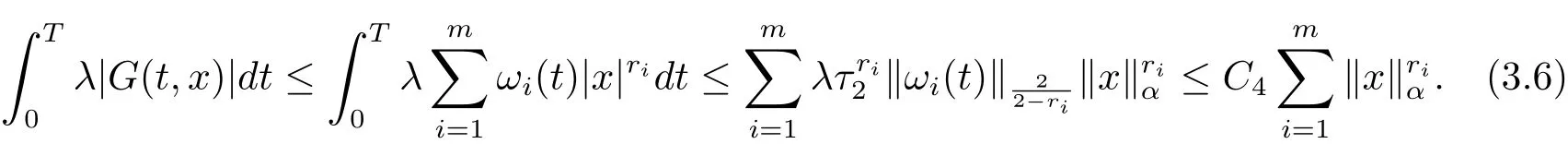

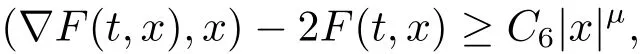
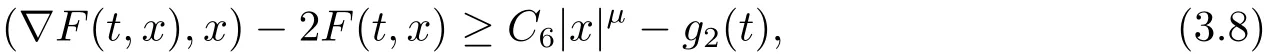
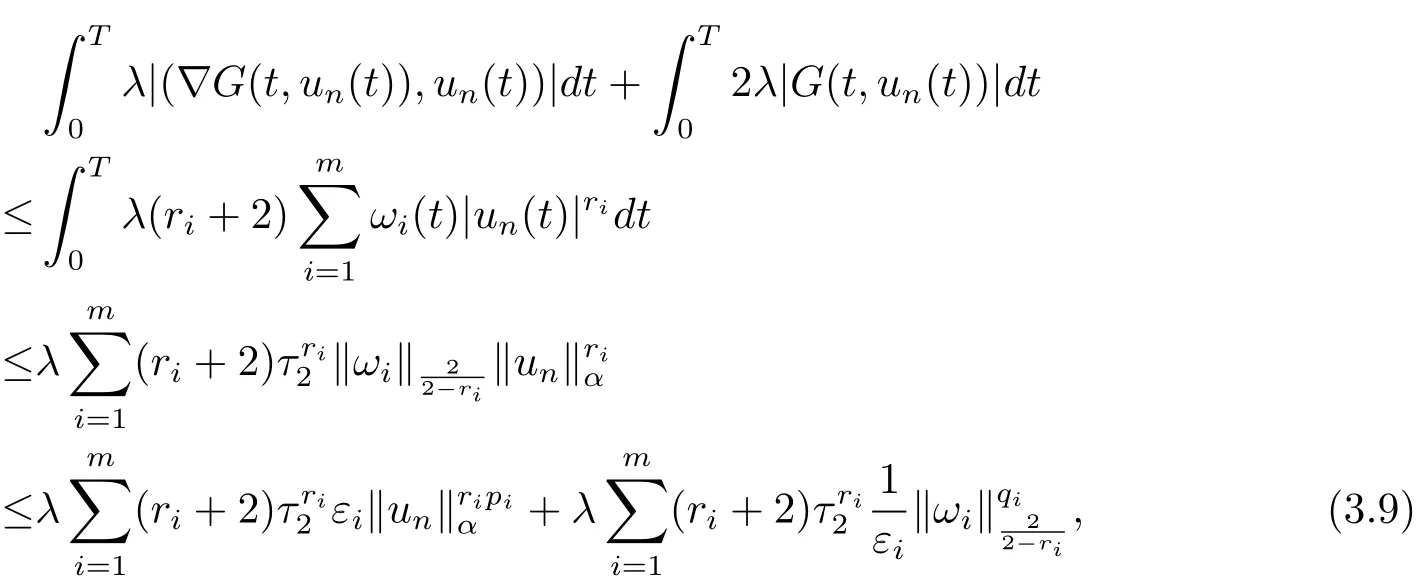
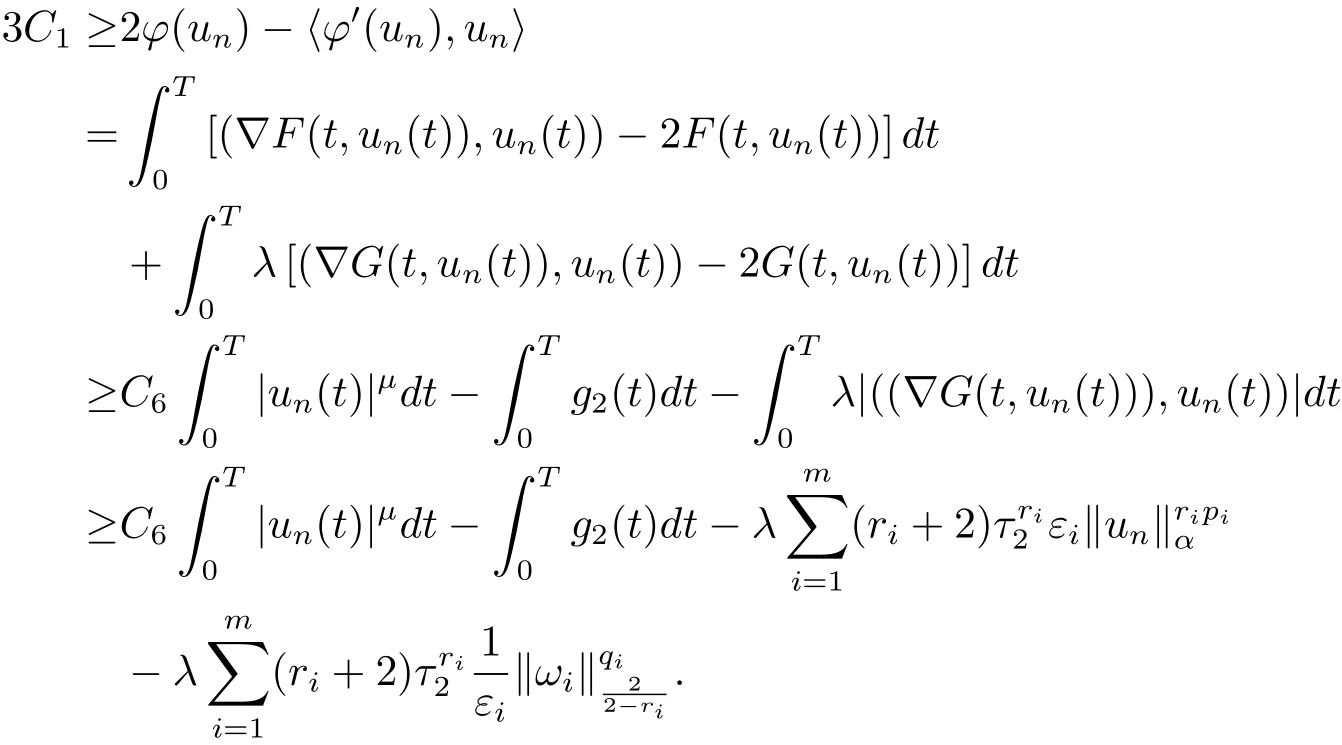
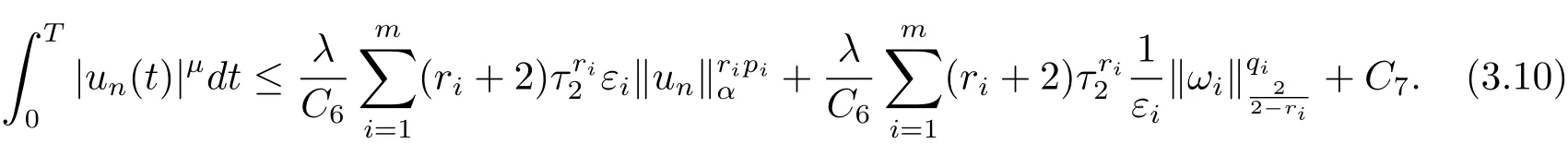
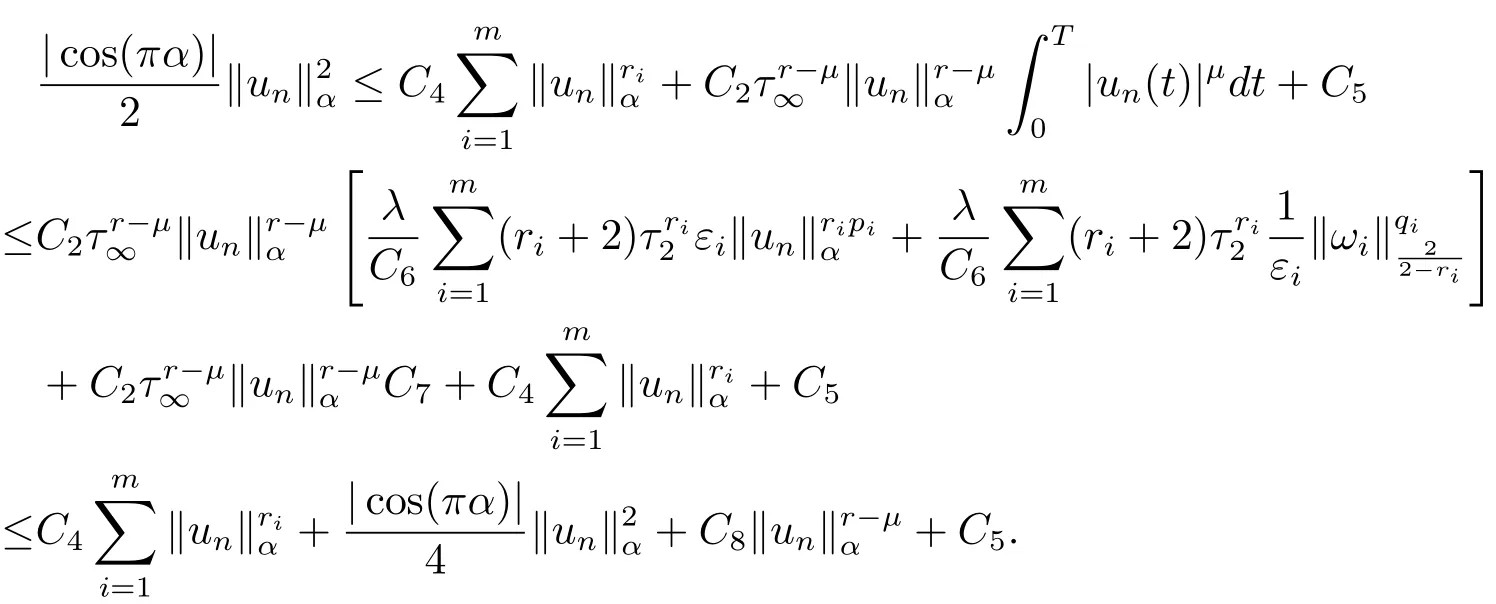

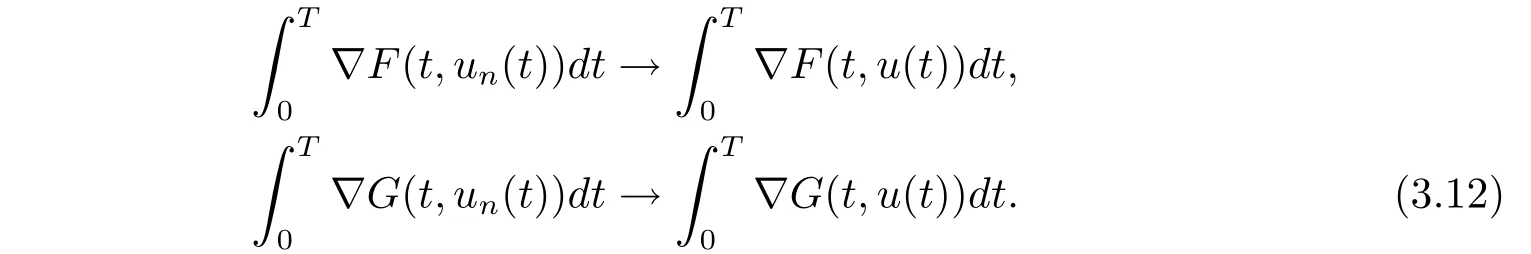

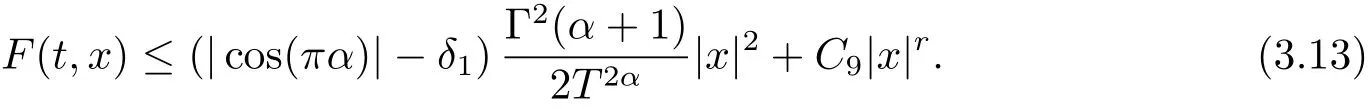
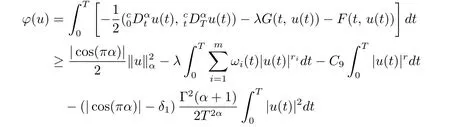
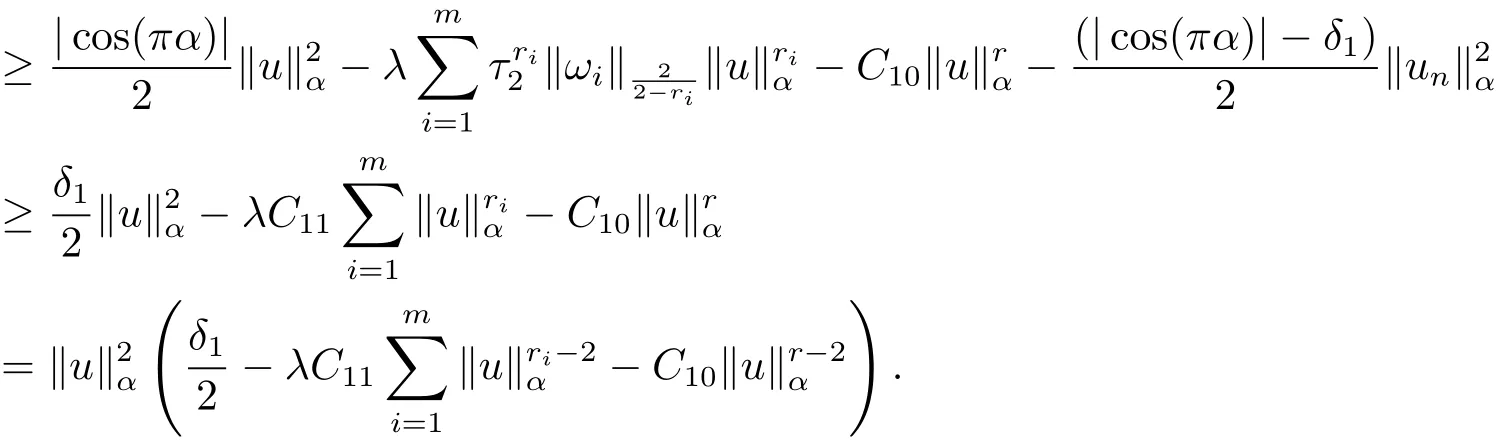
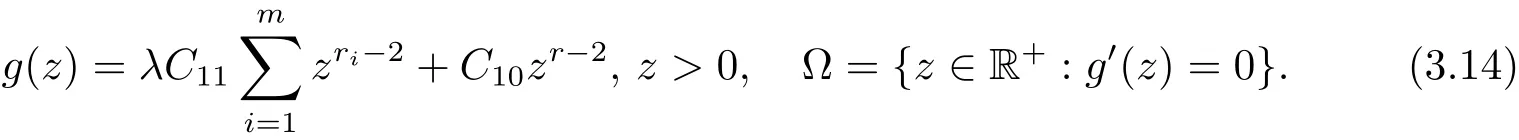
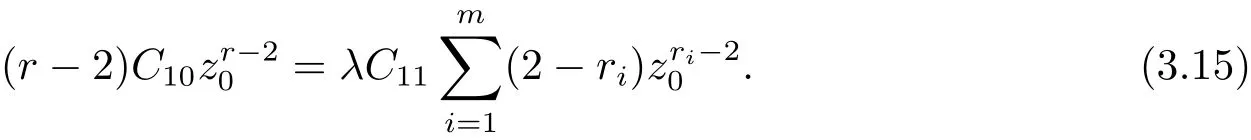
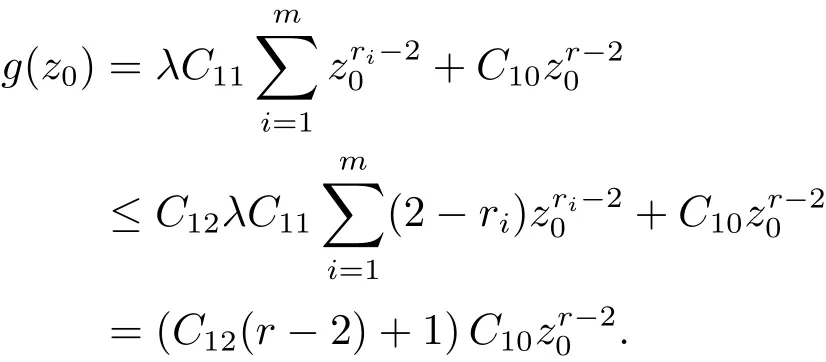

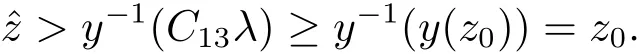
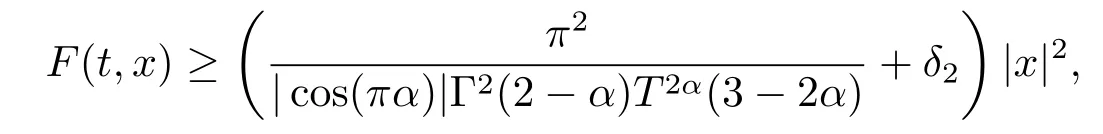
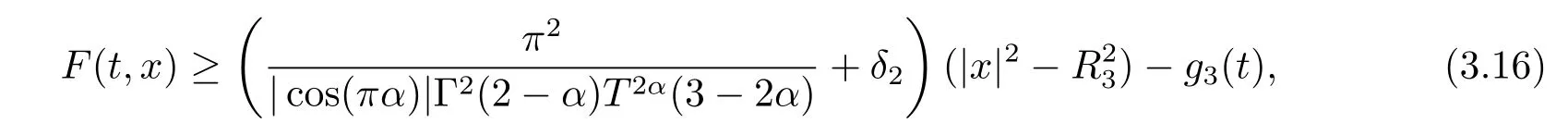
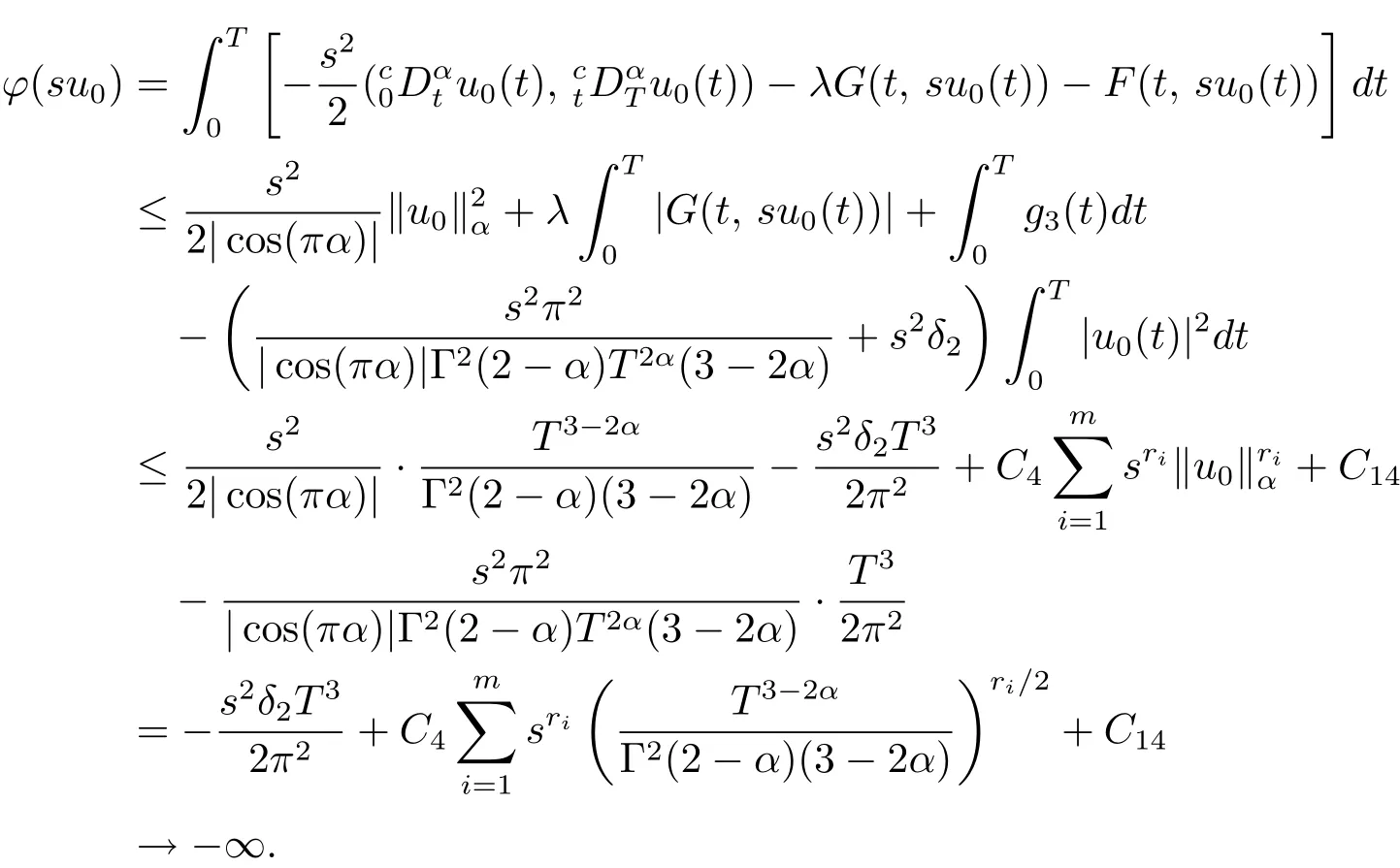
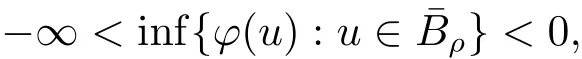
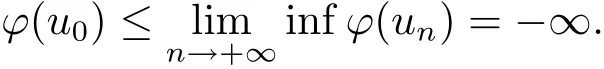


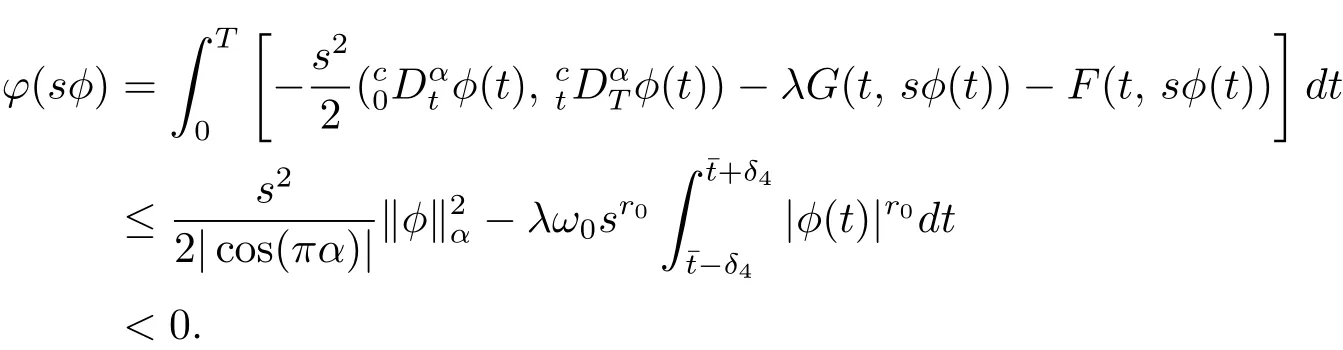
4 例子