关于指数Diophantine方程x2=D2m−Dmpn+p2n

贺艳峰

(延安大学数学与计算机科学学院,陕西延安 716000)

1 引言和结论

设Z,N分别是全体整数和正整数的集合.D>1是正整数,p是适合p-D 的素数.50多年前,陈景润[1]在研究数论中有关本原商高数的Jeśmanowicz猜想时,曾涉及到方程

的求解问题.这是一类指数型的广义Ramanujan-Nagell方程,它与数论、组合数学和编码理论中的很多重要问题的研究有关(参考文献[2]).对此,佟瑞洲在文献[3]中确定了方程(1.1)的所有适合m=1的解(x,m,n);在文献[4]中提出,除了

以外,方程(1.1)适合m>1的解必定满足下列两个条件之一:

(i)D是奇数,p≡1(mod 8),m=2,n=1;

(ii)D是偶数,D含有2kq+1之形素因数,其中q是m的奇素因数.然而,方程(1.1)除了(1.2)以外,显然还有解

不满足上述(i)和(ii).由此可知文献[4]的结果是不完整的.

对于非负整数t,设

其中

本文根据Diophantine方程的性质和若干已知结果,运用初等方法,完整地确定了方程(1.1)适合m>1的所有解,即证明了

定理 除了(1.2)和(1.3)以外,方程(1.1)适合m>1的解仅有

2 若干引理

为了证明定理,首先需要证明下面的几个引理.为此,设X>1,r>1均是正整数,q是奇素数.

引理 2.1如果 Xr−1是素数,则X=2且r是素数.

证 参见文献[5]的定理1.10.1.

引理 2.2 如果Xr+1是素数,则X是偶数且r=2s,其中s是正整数.

证 参见文献[5]的定理1.10.2.

引理 2.3设X>1,r>1均是正整数,q是奇素数,则

(i)

(ii)当X+1≡0(mod q)时,q k(Xq+1)/(X+1),且(Xq+1)/q(X+1)的素因数p满足p≡1(mod 2q);当X+1 6≡0(mod q)时,(Xq+1)/(X+1)的素因数p满足p≡1(mod 2q).

证 参见文献[6].

引理 2.4当 U2t+1,V2t+1适合(1.4)和(1.5)式时,(U,V)=(U2t+1,V2t+1)(t=0,1,···)是方程

的全部解.

证 因为(U,V)=(1,1)是方程(2.1)的最小解,所以从文献[7]第5.3节直接可得本引理.

引理2.5方程组

仅有解(X,Y,Z)=(1,1,1).

证 参见文献[4]的引理6.

引理2.6方程

仅有解(X,Y)=(1,1).

证 参见文献[7]第6.2节.

引理2.7方程

仅有解(X,Y,r)=(78,23,3).

证 参见文献[8]的定理8.1.

引理2.8方程

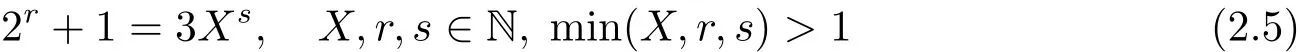
无解(X,r,s).

证 参见文献[9].

引理2.9方程

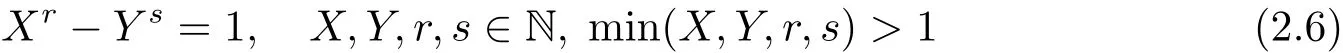
仅有解(X,Y,r,s)=(3,2,2,3).

证 参见文献[10].

引理2.10对于奇素数p,方程

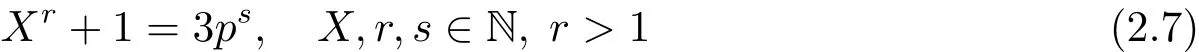
证 设(p,X,r,s)是方程(2.7)的一组解.此时显然X>1.因为当r是偶数时,3-Xr+1,所以r必为奇数;又因r>1,所以r必为奇素数q.

根据引理2.9可知,方程(2.7)仅有解(p,X,r,s)=(3,2,3,1)适合p=3.当p 6=3时,因为从方程(2.7)可知3|Xr+1且32-Xr+1,所以q>3.设

根据引理2.3,从(2.7)式可知d=1或p且q=p.

如果d=1,则从(2.7)式可知

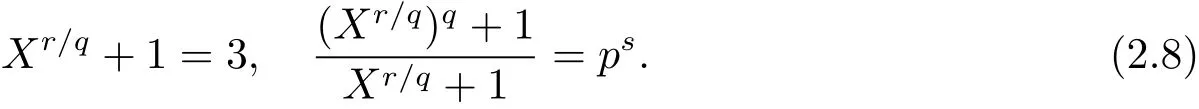
由于从(2.8)式中第一个等式可得X=2,且r=q,又结合引理2.8和(2.8)式的第二个等式可得s=1,故有其中q是大于3的奇素数.

如果d=p,且q=p,则根据引理2.3的结论(ii),从(2.7)式可得Xr/q+1=3ps−1≥3p,以及p=(Xr+1)/(Xr/q+1)>Xr/q+1>p,这就得出一对矛盾不等式,故d=p不成立.引理证完.

引理2.11对于奇素数p和q,方程

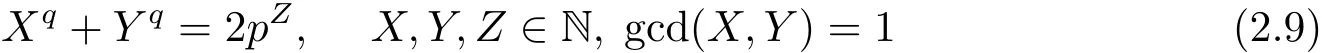
无解(X,Y,Z).

证 设(X,Y,Z)是方程(2.9)的一组解.因为p>1,所以(X,Y)6=(1,1),故有X+Y>2.由于(Xq+Yq)/(X+Y)是大于1的奇数,所以从(2.9)式可得

因为从(2.10)式可知p|gcd(X+Y,(Xq+Yq)/(X+Y)),所以q=p.然而,由于q k(Xq+Yq)/(X+Y),所以(2.10)式中的 s=1,并且可得q=p=(Xq+Yq)/(X+Y)>q,矛盾.因此方程(2.9)无解.引理证完.

引理2.12当r是大于2的正整数时,方程

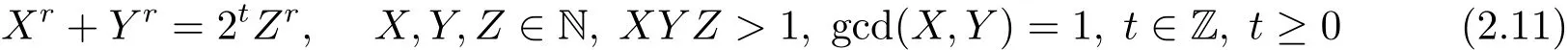
无解(X,Y,Z,t).

证 参见文献[11].

3 定理的证明

设(x,m,n)是方程(1.1)的一组满足m>1的解.

首先讨论p=2时的情况.此时D是大于1的奇数,方程(1.1)可表示成

因为D是奇数,所以从(3.1)式可知x也是奇数,故从x2≡D2m≡1(mod 8)以及0≡x2−D2m≡−2n(Dm−2n)(mod 8)可知n≥3.

从(3.1)式可得

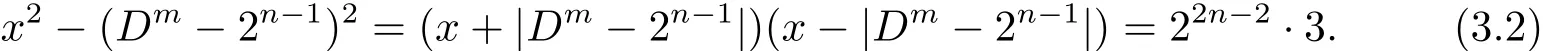
因为gcd(x+|Dm−2n−1|,x−|Dm−2n−1|)=2,所以从(3.2)式可得

或

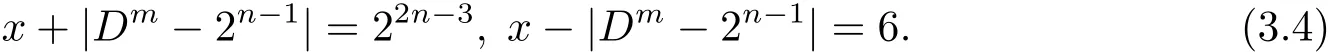
当(3.3)式成立时,在其中消去x可得

由于 n ≥ 3,所以 22n−4·3−1>22n−3>2n−1,故从 (3.5)式可知 Dm>2n−1以及

从(3.6)式可得

因为n≥3,所以从(3.7)式可知m必为奇数,故有m≥3.又因(Dm+1)/(D+1)是奇数,所以从 (3.7)式可得 D+1 ≥ 2n−1,以及 2n−1>2n−3·3+1 ≥ (Dm+1)/(D+1)≥(D3+1)/(D+1)=D2−D+1>D+1≥2n−1这一矛盾.

当(3.4)式成立时,在其中消去x可得

如果n=3,则从(3.8)式可得|Dm−4|=1.然而,因为m>1,这是不可能的.如果n>3,

则因 22n−4−3>2n−1,所以从 (3.8)式可知 Dm>2n−1以及

由于 gcd(2n−2−1,2n−2+3)=1,故从 (3.9)式可得

然而因为m>1,所以根据引理2.9,从(3.10)式中第一个等式可知n=3,又从第二个等式可得bm=5这一矛盾.

从以上分析可知,当p=2时,方程(1.1)没有适合m>1的解(x,m,n).

其次讨论p是奇素数时的情况.此时从(1.1)式可知

因为p-D,所以p-x且gcd(2x+|2Dm−pn|,2x−|2Dm−pn|)=1,故从(3.11)式可得

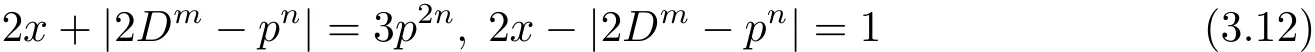
或

现分别按照(3,12)式和(3.13)式成立这两种情况进行讨论.

情况I(3.12)式成立.从(3.12)式可得

和

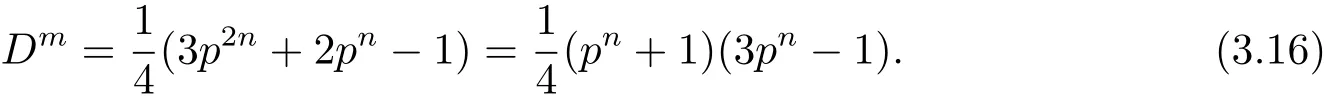
如果pn≡1(mod 4),则因与是互素的奇数,故从(3.16)式可得

从(3.17)式可得

和

由于m>1,根据引理2.11,从(3.18)式可知m没有奇素因数,所以m=2s,其中s是正整数.同时,因为从(3.18)式可知(a,b)6=(1,1),所以根据引理2.6,结合(3.19)式可知s<2.因此s=1,即m=2.将此代入(3.17)式中第一个等式,可得

当n>2时,根据引理2.7,结合(3.20)式可知,仅有(a,p,n)=(78,23,3),然而,此时从(3.17)式中第二个等式可得=18250,故这是不可能的.

当n=2时,联合(3.19)式和(3.20)式可知,方程组(2.2)有解(X,Y,Z)=(p,a,b)6=(1,1,1).然而,根据引理2.5可知这是不可能的.

当n=1时,根据引理2.4,联合(3.14),(3.19)和(3.20)式可得形如(1.6)式的解.

如果pn≡3(mod 8),则因是与3pn−1互素的奇数,后者是偶数,所以从(3.16)式可得

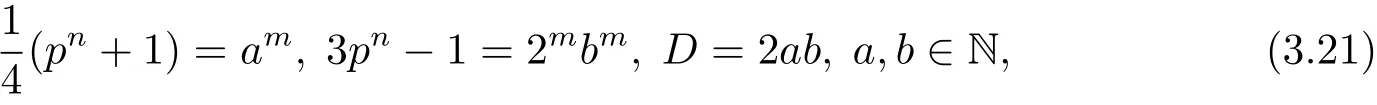
因为m>1,所以根据引理2.10,从(3.21)式中第二个等式可得

或

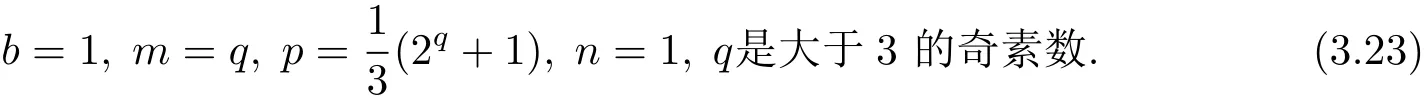
当(3.22)式成立时,联合(3.14)和(3.21)式可得解(1.2).当(3.23)式成立时,从(3.21)式中第一个等式可得

如果pn≡7(mod 8),则因是与pn+1互素的奇数,后者是偶数,所以从(3.16)式可得

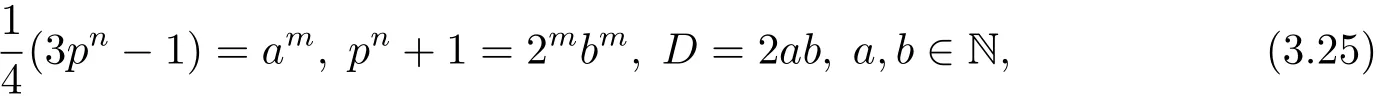
因为m>1,所以根据引理2.9,从(3.25)式中的第二个等式可知n=1,以及

再根据引理2.1,从(3,26)式可知b=1.将此代入(3.25)式中的第一个等式可得

然而,由于1<3·2m−2−1<2m,所以(3.27)式不可能成立.

从以上分析可知:方程(1.1)仅有解(1.2)和(1.6),满足m>1和(3.12)式.

情况II(3.13)式成立.从(3.13)式可得

和

如果pn≡1(mod 8),则因是与pn−1互素的奇数,后者是偶数,所以从(3.30)式可得

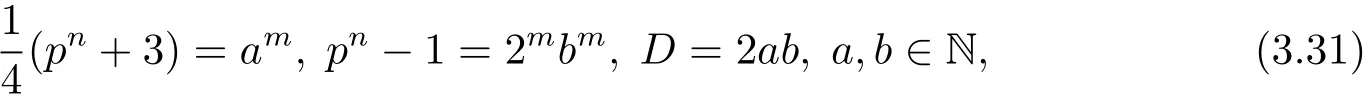
因为m>1,而且从(3.13)式可知p 6=3,所以根据引理2.9,从(3.31)式中第二个等式可得n=1,以及

再根据引理2.2,从(3.32)式可知m必为偶数.然而,此时在(3.31)式中消去pn,可得1=am−2m−2bm≥ am/2+2m/2−1bm/2>1,矛盾.

如果pn≡3(mod 4),则因与是互素的奇数,所以从(3.30)式可得

然而,因为m>1,又从(3.33)式可知b>a≥1,所以在(3.33)式中消去pn,可得

矛盾.

如果pn≡5(mod 8),则因是与pn+3互素的奇数,后者是偶数,所以从(3.30)式可得

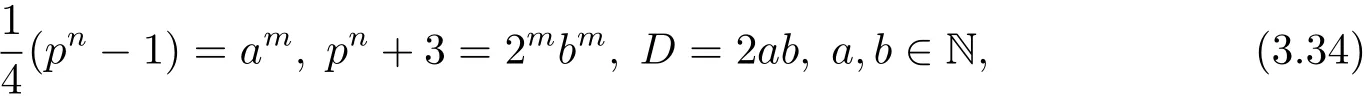
在(3.34)式中消去pn,可得

显然,从(3.35)式可知m必为奇数.又因m>1,所以根据引理2.12,从(3.35)式可知,仅有m=3以及a=b=1.将此代入(3.28)和(3.34)式即得解(1.3).由此可知,方程(1.1)仅有解(1.3)满足m>1以及(3.13)式.

综合以上所有,定理证完.