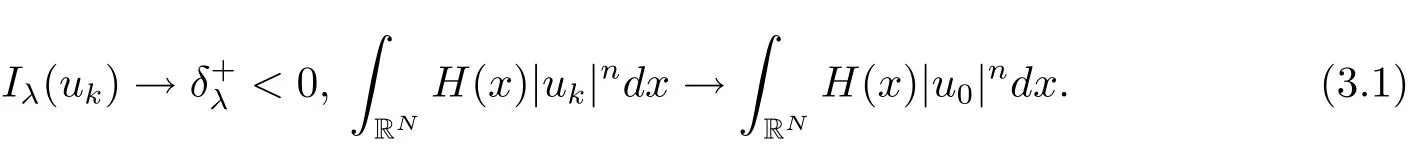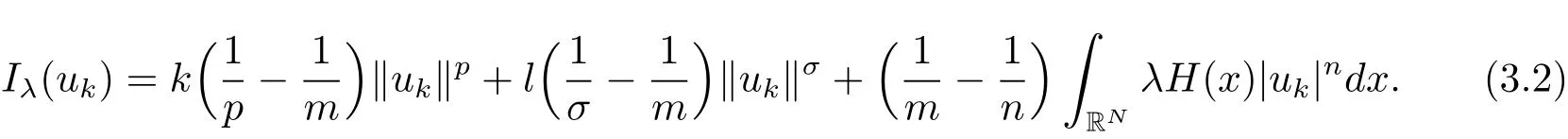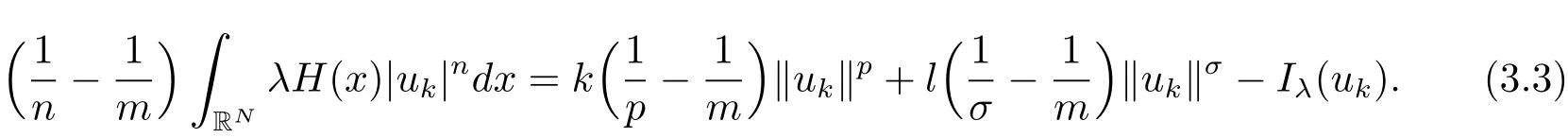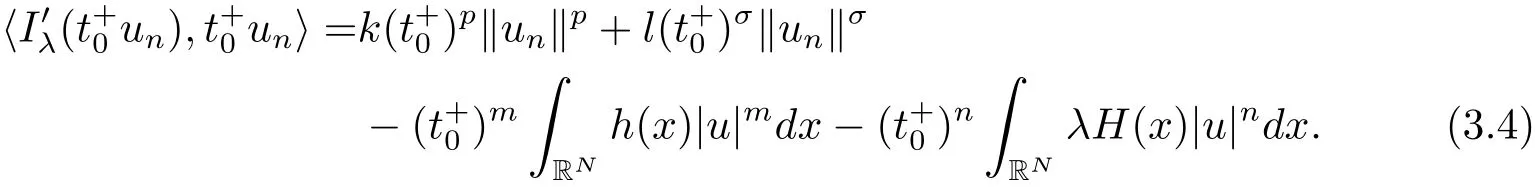一类非局部椭圆方程正解的存在性
2019-04-13陈林
陈林
(伊犁师范学院数学与统计分院,新疆伊宁 835000)
1 引言
椭圆型方程是偏微分方程理论的一个重要组成部分,其解的存在性问题具有很高的学术价值和理论价值,是偏微分方程领域中一个重要的研究课题.文献[1]研究了如下拟线性椭圆边值问题
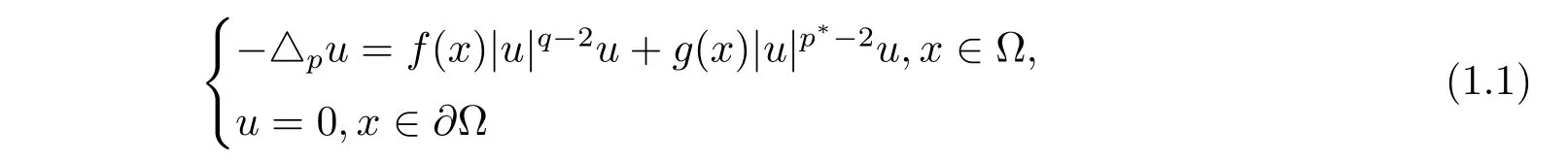
近年来,对非局部椭圆方程的研究日益受到人们的重视[2–5].本文研究如下一类非局部椭圆方程
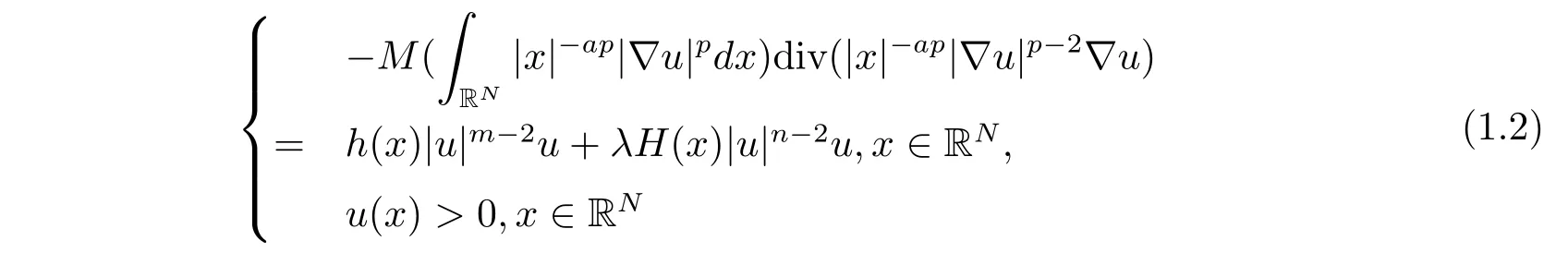
非平凡弱解的存在性,其中λ>0是实参数,1
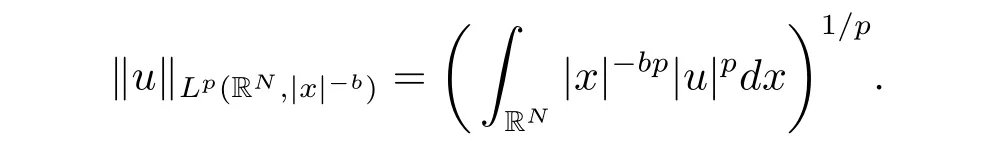

的完备化空间.
由文献[8]可知,存在一常数S>0使得
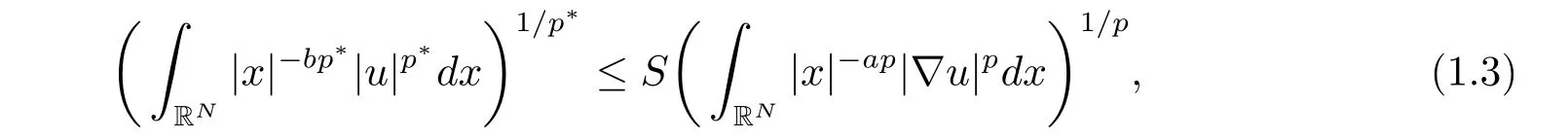
其中−∞ 为研究问题的方便,做如下假设: 本文的主要结果为 定理1.1 若条件(A1)–(A3)成立.则存在正数λ1使当λ∈(0,λ1)时,问题(1.2)至少具有两个正解. 定义2.1若u∈X且对于任意的ϕ∈X有 成立,则称u为问题(1.2)的一个弱解. 显然问题(1.2)具有变分结构.设Iλ(u)是问题(1.2)所对应的Euler泛函,其具体表达式为 其中σ=p(τ+1).则Iλ(u)∈C1(X,R)且对于任意的ϕ∈X 有 特别地, 由于Iλ在X上无界,因此引入Nehari流形 从而当u∈Nλ时,有 引入纤维环映射 φu:t∈ R+7→ Iλ(tu),则 易见,u∈Nλ当且仅当(1)=0.更一般地,(t)=0当且仅当tu∈Nλ.将Nλ分成 由于当u∈Nλ时,(1)=0,从而 引理2.2 Iλ是强制的且在Nλ上有下界. 证 由Hölder不等式及不等式(1.3),得 由于n 引理2.3存在λ0>0使得当λ∈(0,λ0)时=∅. 将(2.18)及(2.19)式运用于(2.21)式得 从而 由此可得λ≥λ0,矛盾!因此,存在λ0>0使当λ∈(0,λ0)时=∅. 引理2.4假定u0是Iλ在Nλ上的一个局部极小值点.如果u06∈,则u0是Iλ(u)的一个临界点. 证 设 由于u0∈Nλ,从而 然而 因此,如果u06∈,则.进而由(2.25)式知µ=0.从而.证毕. 由引理2.3,当λ∈(0,λ0)时,.定义 (2)存在k0>0,使得≥k0. 证(1)设u∈N+λ,则由(2.13)和(2.17)式得 从而 则 z0(t)=tp−n−1E(t),其中 则 令E0(t)=0得 则E(t)在[0,t∗)单调递增,在(t∗,+∞)单调递减.从而E(t)在t∗处取得最大值.由于E(0)=k(p−n)kukp>0,E(+∞)=−∞,因此存在唯一的tl>t∗>0,使得E(tl)=0且当t∈[0,tl)时函数z(t)递增,当t∈(tl,+∞)时,函数z(t)递减;在tl处取得最大值.特别地,当l=0时,有 由E(t0)=E(tl)=0可知t0≤tl.从而 证 设 则 从而由函数z(t)的特性可知存在0 以及z0(t+)>0>z0(t−).由于Ψ1(t)=tn+1z0(t),从而t+u∈,t−u∈N−λ.由于当t∈ [0,t+)时,<0;当 t∈ [t+,tl)时,(t)>0,从而另外,易验证当 t∈ [t+,t−)时,(t)>0;当 t∈ [t−,+∞)时,(t)<0;当 t∈ [0,t+]时,Ψ2(t)≤ 0.又由于t−u∈,从而由引理2.5中的(2)可知Ψ2(t−)>0.从而由Ψ2(t)的单调性可知证毕. 则η(0+)=−∞,η(+∞)=0,η(t)在某个t=Tl>0处取得最大值. 引理2.8假定(A1)–(A3)成立.若{uk}在X中收敛于u∈X,则存在{uk}的一个子列(不妨仍记为{uk})满足 证 只证明(2.42),(2.41)式的证明是类似的,在此略去.因为从而对于任意ε>0,存在R0>0使得 其中Br={x∈RN:|x|≤r}而.由于{uk}在X中弱收敛于u,则{uk}在X中有界且{uk}在空间中弱收敛于u.进而,由不等式(2.43)推出{uk}在空间中有界.因此,存在的子列(不妨仍记为)使得在中弱收敛于u,在RN中几乎处处收敛于u.从而对于任意k≥1存在与k无关的常数M使得 因此对于足够大的k成立, 另一方面,由Hölder不等式,当k足够大时,有 引理3.1如果0<λ<λ1,则泛函Iλ在上存在一个最小值点且有 (1)Iλ(u0)=; (2)u0是问题(1.2)的一个非平凡的非负解. 证由引理2.2知Iλ在Nλ上有下界(从而在上有下界),因此存在一个极小化序列使得因为泛函Iλ是强制的,所以{uk}在X 中有界.不失一般性,可假定{uk}在X中弱收敛于u0.由引理2.5和引理2.8可得,当k→∞时,有 由(2.8)式得 因此 接下来证明{un}在X中强收敛于. 另一方面,由{un}⊆可知,且当0 这与下确界的定义矛盾!故{un}在X中强收敛于.从而 引理3.2假定λ∈(0,λ1),则泛函Iλ在上有极小值点使得 证由引理2.2知Iλ在上是强制的.从而存在一极小化序列{uk}⊆使得 由于Iλ强制,从而{uk}在X中有界.因此,存在{uk}的一个子列(不妨仍记为{uk})在X中弱收敛于元.由引理2.5可知,当u∈时,Iλ(u)>0,因此有 进而由(2.9)式得 接下来证明{uk}在X中强收敛于.假若不然,则有 由于uk∈,从而当t≥0时,Iλ(uk)≥Iλ(tuk).因此有 这与δ−的定义矛盾!从而{uk}在X中强收敛于.从而 定理1.1的证明 由引理3.1和引理3.2知,当λ∈(0,λ1)时,问题(1.2)有两个非平凡的正解∈和∈.又由于∩=∅,从而和是问题(1.2)的两个不同的正解.定理1.1证毕!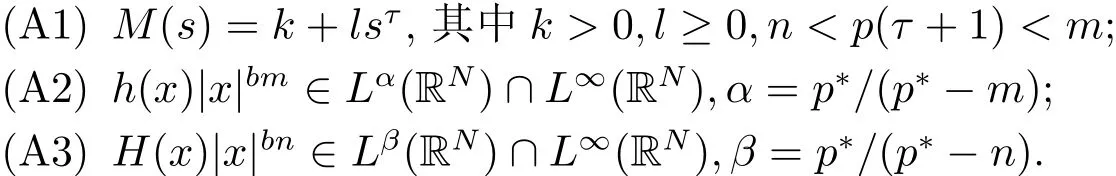
2 预备知识
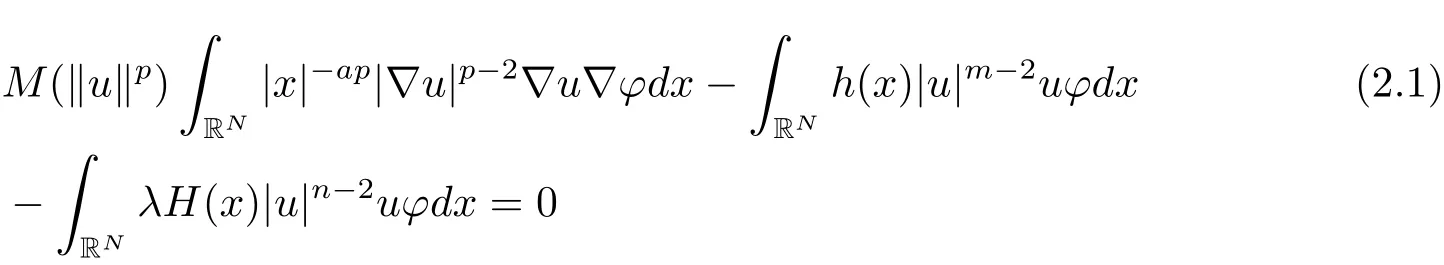
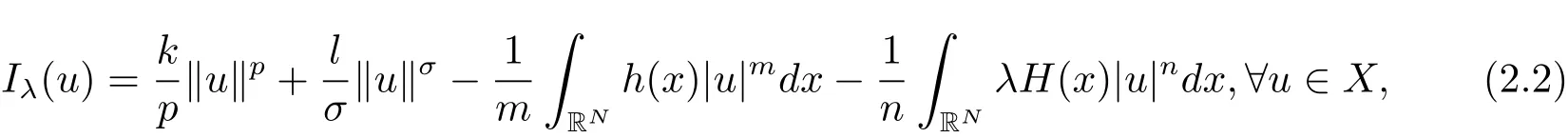
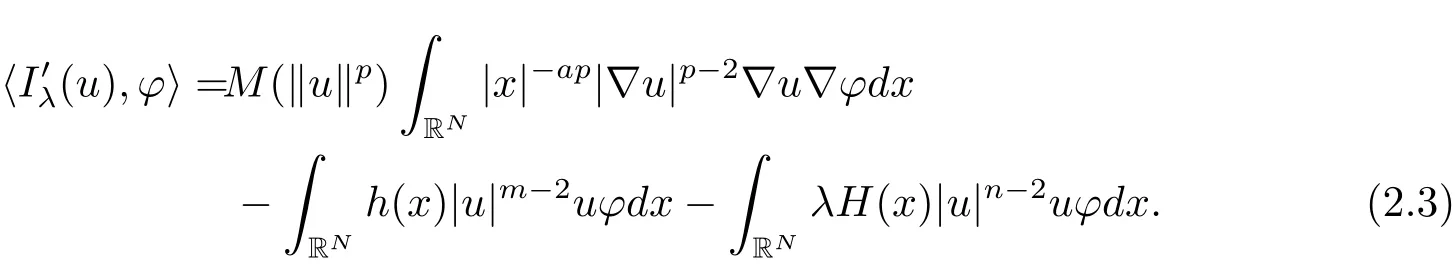
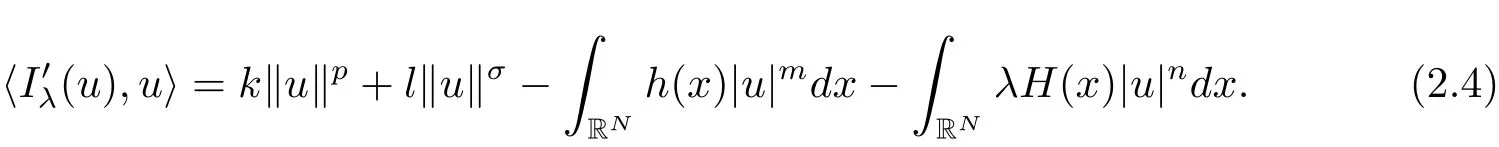



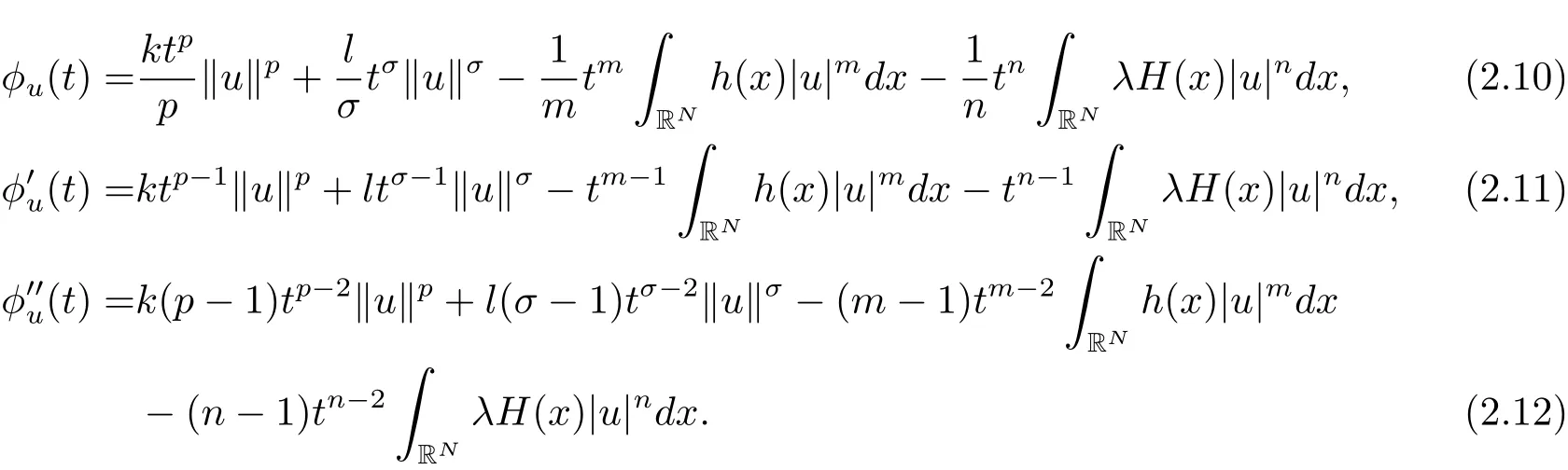


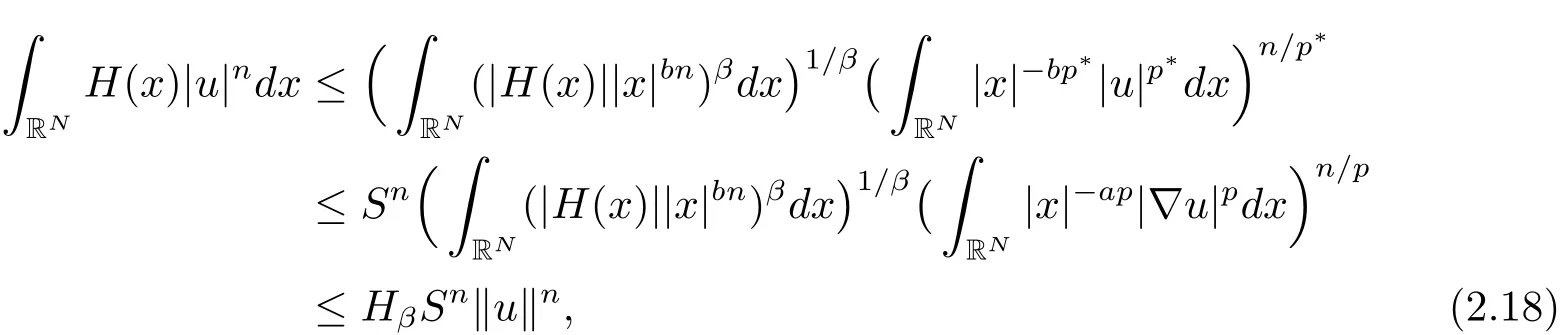
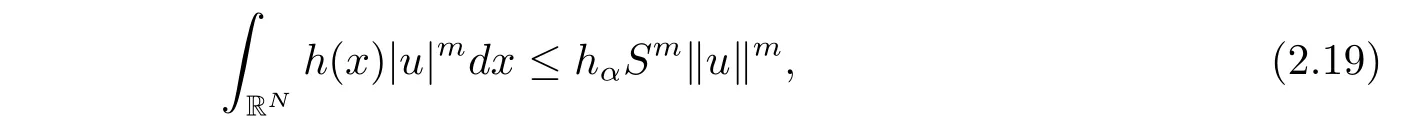
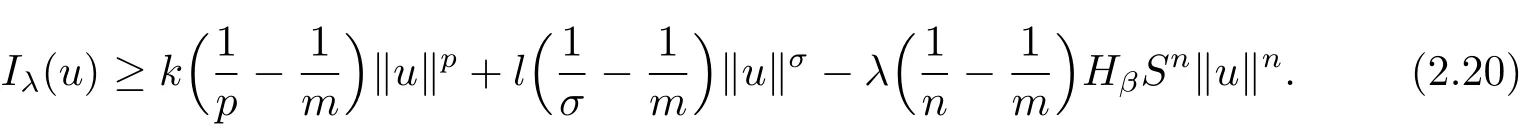



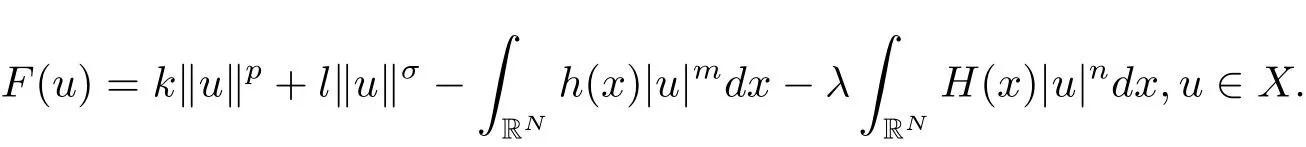



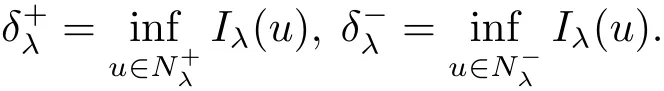

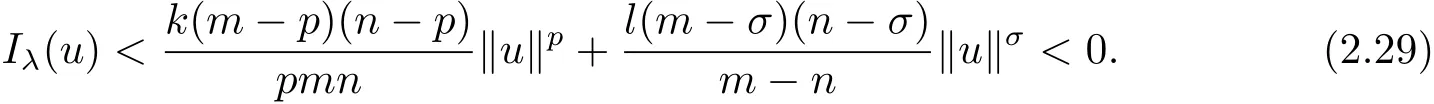
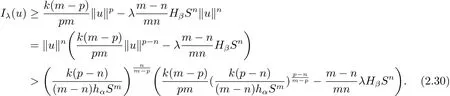

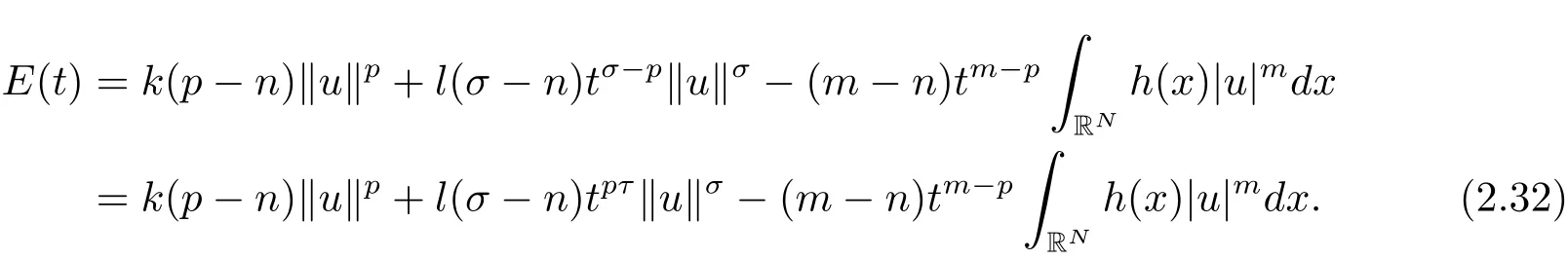
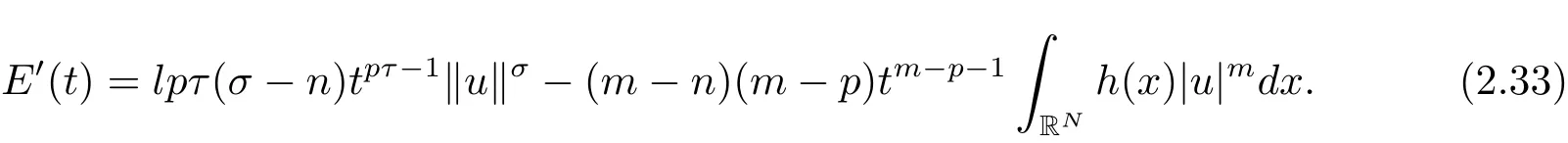


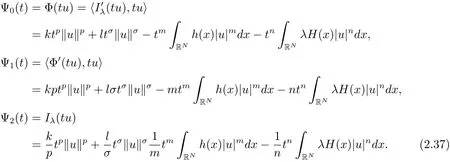
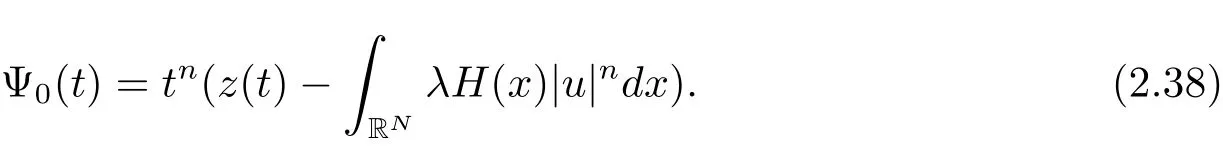
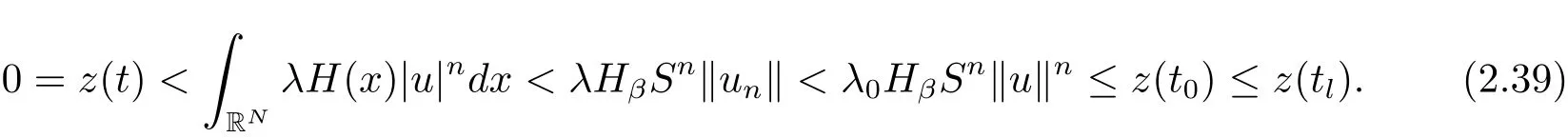
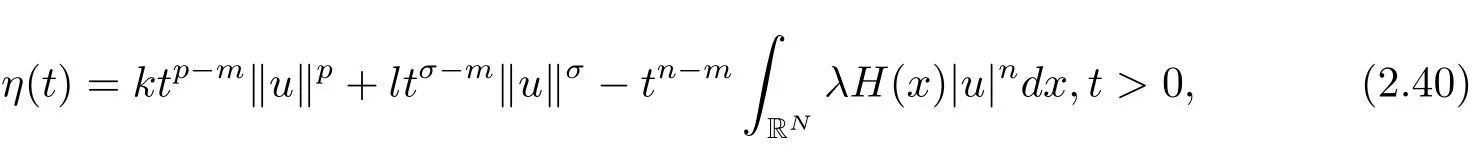
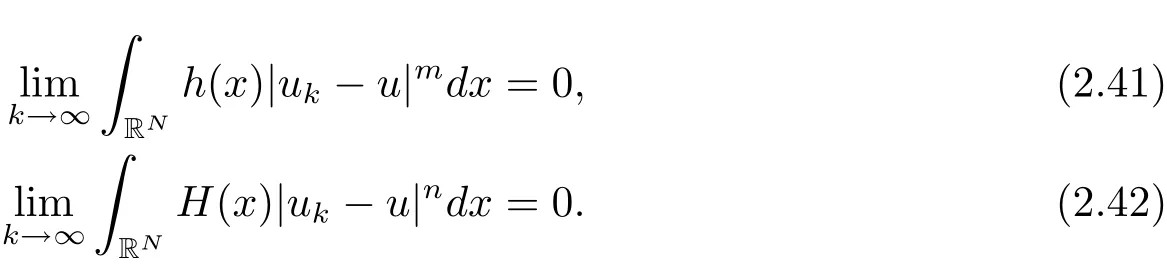
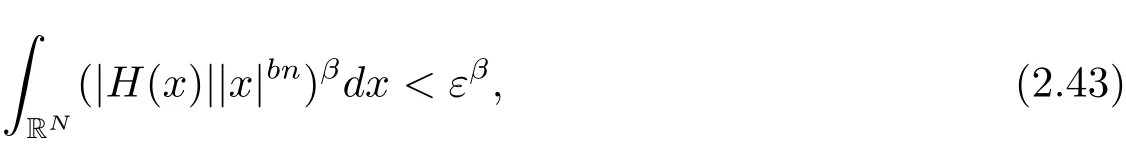
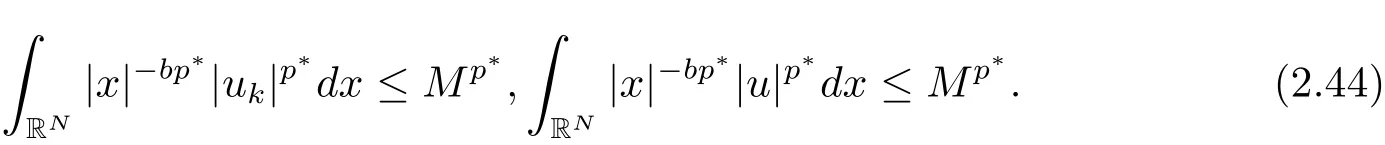


3 正解的存在性