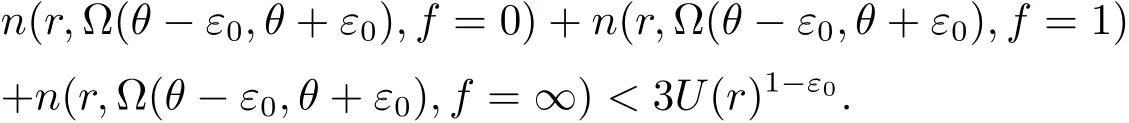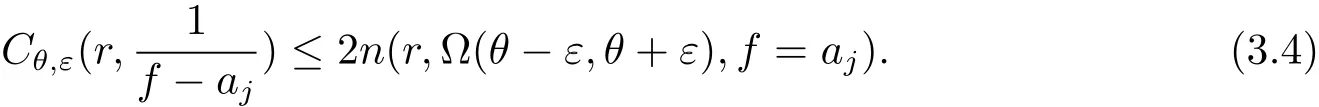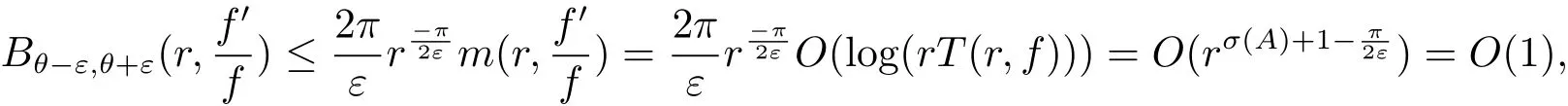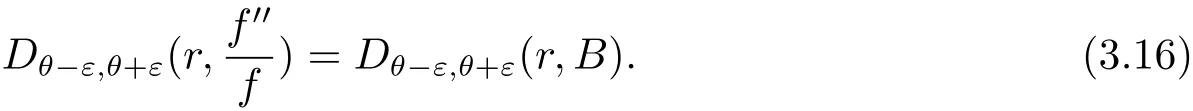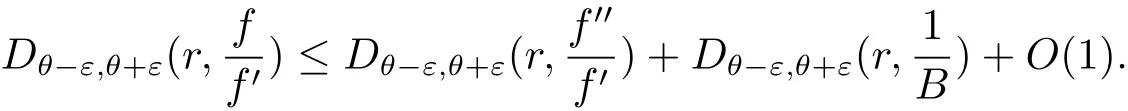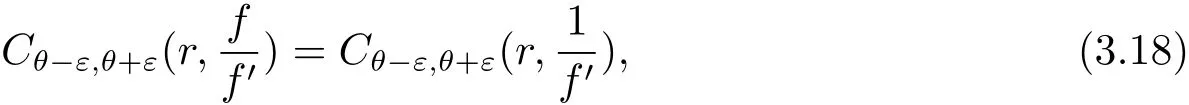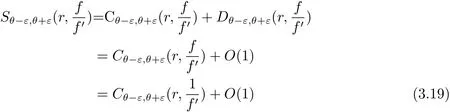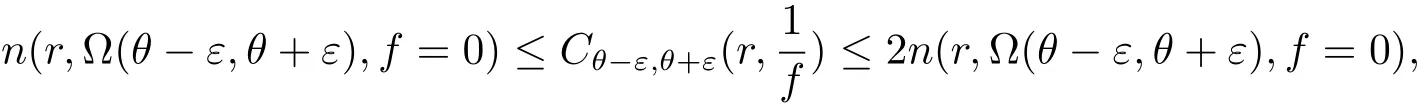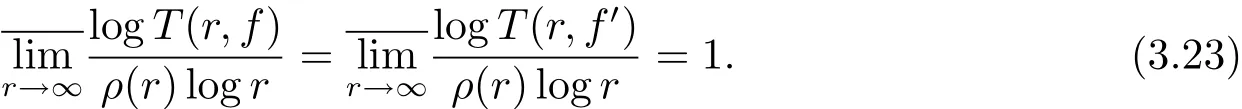线性微分方程解在角域内的性质
2019-04-13魏文龙魏冬梅黄志刚
魏文龙,魏冬梅,黄志刚
(苏州科技大学数理学院,江苏苏州 215009)
1 引言及主要结果
本文主要研究非齐次线性微分方程f00+Af0+Bf=F中方程解的Borel方向和非齐次项之间的关系.关于奇异方向中Borel方向的发展已经有了较长的时间,本文所讨论的是精确级Borel方向的某些性质,作为对Borel方向的一个发展和补充,同时给出了亚纯函数的精确级Borel方向和零点聚值线的部分性质.假设读者熟悉亚纯函数Nevanlinna理论的基本定义,定理和标准符号[1−4].为了叙述方便,给出以下定义.
定义1.1设0≤α<β<2π,复平面上的角域和扇形域分别定义为

设f(z)是复平面C上的亚纯函数,对于任意给定的ε>0,亚纯函数f(z)在角域Ω(θ− ε,θ+ε)上的零点收敛指数 λθ,†(f)定义为


其中 bv=|bv|eiβv(v=1,2,···) 是 f(z) 在角域 Ω(α,β)内极点 (不计重数),Sα,β(r,f)称为f(z)在角域中Nevanlinna特征函数,Cα,β(r,f)称为f(z)在角域上极点的计数函数(重级极点按重数计算),则亚纯函数在角域上的级定义为

定义1.3设f(z)是无限级亚纯函数,实函数ρ(r)称为f(z)的熊庆来无限级,如果ρ(r)满足如下性质:

上述定义最先为熊庆来所介绍,关于ρ(r)的存在性,庄圻泰给出了其简单的证明.
定义1.4射线J:argz=θ称为f(z)的1条ρ(r)级Borel方向,如果
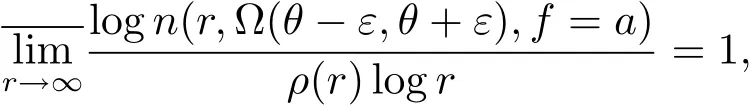
∀ε>0和任意的复数a∈C∞成立,最多除去2个例外的a值.
射线J:argz=θ称为f(z)的ρ(r)级零点聚值线,如果

其中n(r,Ω(θ−ε,θ+ε),f=a)表示f(z)在扇形域Ω(θ,ε,r)={z:θ−ε 在文献[5]中,伍胜健首次研究了二阶微分方程的解的零点的幅角分布,发现了方程解的乘积的零点聚值线和Borel方向之间的联系,给出了如下的结论. 定理A 设A(z)是一个级为ρ<∞的超越整函数和f1,f2为方程f00+A(z)f=0的两个线性无关解,记E=f1f2.再设E的零点收敛指数λ(E)=∞,则射线argz=θ是E的一条∞级Borel方向的充分必要条件是λθ(E)=∞. 定理A中对于Borel方向的级的估计还是比较粗糙的,吴昭君就针对定理A给出了猜想,将定理A中的无穷级换成熊庆来的无限级,是否能得到相类似的结论?在文献[6]中,吴昭君给出了证明,即定理B. 定理B 设A(z)是级为ρ<∞的超越整函数,f1,f2为方程f00+A(z)f=0的两个线性无关解.令E=f1f2,再设λ(E)=∞,ρ(r)是E的一个无限级,则射线argz=θ是E的一个ρ(r)级Borel方向的充分必要条件是 从定理A到定理B,不难看出,定理B对Borel方向的估计比定理A要精确得多,使得结论得到了进一步的完善,这提供了一个思路.在文献[10]中,黄志刚、王珺研究了二阶非齐次线性微分方程的非齐次项和方程解的Borel方向之间的关系,得到了定理C. 定理C 假设A(z)和B(z)是有限级的整函数,F(z)是无穷级的超越整函数,并且满足max{σ(A),σ(B)}<σ(F)=∞,如果argz=θ是F(z)的一条Borel方向,则argz=θ也是方程f00+Af0+Bf=F的任意非平凡解的一条Borel方向. 在定理B的启发之下,同时在定理C的基础之上,研究非齐次方程解的精确级Borel方向和方程非齐次项之间的关系,得到定理1. 定理1 假设A(z)和B(z)是有限级的整函数,F(z)是无穷级的超越整函数,如果argz=θ是F(z)的一条ρ(r)级Borel方向,则argz=θ也是方程f00+Af0+Bf=F的任意非平凡解的一条ρ(r)级Borel方向. 在文献[8]中,Rossi和Wang讨论了方程f00+A(z)f=0整函数解与其导数零点之间的关系,得到 定理D 假设A(z)是一个有限级的超越整函数,当argz=θ是复平面上任意一条射线,于是方程f00+Af=0的任意解有λθ(f)=∞当且仅当λθ(f0)=∞. 结合定理D的结论,不难得出一个问题,方程f00+Af=0的任意整函数解的精确级零点聚值线和方程解导数的零点聚值线是否有这样的关系?经过讨论,得到了肯定的回答. 定理2 设B(z)为有限级的超越整函数,argz=θ是从原点出发的一条射线.则对方程f00+B(z)f=0的任意非平凡解f,都有argz=θ是f的精确级零点聚值线当且仅当argz=θ是f0的精确级零点聚值线. 此外,我们知道定理1的结论是对定理C的改进,使得对Borel方向的增长级的估计更加精确.关于定理1的证明将主要利用定理3的结论以及定理3的推论,从新的角度来研究方程解的性质. 定理3 令h(z)=f(z)g(z),其中f(z)和g(z)都是复平面上的亚纯函数.设ρ(r)是h(z)的一个无限级,射线argz=θ是h(z)的一条ρ(r)级Borel方向,则射线argz=θ一定是f(z)或者g(z)的一条ρ(r)级Borel方向. 由定理3的结论,可以给出以下4个推论. 推论1 令h(z)=f(z)g(z),其中f(z)和h(z)都是复平面上的亚纯函数.设ρ(r)是h(z)的一个无限级,并且射线argz=θ是f(z)的一条ρ(r)级但不是g(z)的ρ(r)级Borel方向,则argz=θ必是h(z)的一条ρ(r)级Borel方向. 推论2是推论1的推广.推论1是两个亚纯函数的乘积,推论2是多个亚纯函数的乘积所对应的结论. 推论 2 令h(z)=f1(z)f2(z)···fn(z),其中fi(z)(i=1,2,···,n)都是复平面上的亚纯函数.设ρ(r)是h(z)的一个无限级,并且射线argz=θ是某一个fm(z)的一条ρ(r)级Borel方向但不是fn(z)(n 6=m)的ρ(r)级Borel方向,则argz=θ必是h(z)的一条ρ(r)级Borel方向. 推论3主要讨论两个亚纯函数之和关于精确级Borel方向的结论. 推论3 令h(z)=f(z)+g(z),其中f(z)和g(z)都是复平面上的亚纯函数.设ρ(r)是h(z)的一个无限级,并且射线argz=θ是h(z)的一条ρ(r)级Borel方向,则argz=θ必为f(z)或者g(z)的一条ρ(r)级Borel方向. 下面推论4是推论3的推广,推论4将直接用于定理1的证明中. 推论 4 令 h(z)=f1(z)+f2(z)+···+fn(z),其中fi(z)(i=1,2,···,n)都是复平面上的亚纯函数.设ρ(r)是h(z)的一个无限级,并且argz=θ为h(z)的一条ρ(r)级Borel方向,则argz=θ必为某一个fi(z)的一条ρ(r)级Borel方向. 为了定理的证明,需要下面的引理. 引理2.1[1](i)设f(z)为角域Ω(α,β)(0<β−α≤2π)上的非常数亚纯函数,则∀a∈C,有 其中当r→∞ 时,ε(r,a)=O(1). (ii)对于任意的r 引理2.2[1]设f(z)为角域Ω(α,β)(0<β−α≤2π)上的非常数亚纯函数,则∀aj∈C∞,j=1,2,···,q,有 引理2.3[9]设f(z)是复平面上的一个无限级亚纯函数,ρ(r)是f(z)的一个级,射线L:argz=θ0是函数f(z)的ρ(r)级Borel方向的充分必要条件是对于任意的 引理2.4[10]设f(z)是复平面上的一个亚纯函数,在角域Ω(α,β)(0<β−α≤2π)内,f(z)和具有相同的Borel方向. 引理2.5[8]设f(z)是复平面上的一个亚纯函数,在角域Ω(α,β)(0<β−α≤2π)内,a为任意一个有穷复数,则函数f(z)和f(z)+a必有相同的Borel方向. 引理2.6[11]设f(z)是无限级亚纯函数,其型函数为U(r)=rρ(r),则射线argz=θ0是f(z)的ρ(r)级Borel方向的充分必要条件是:射线argz=θ0是它的导数f0(z)的ρ(r)级Borel方向. 在给出定理1的证明之前,先给出定理3及其推论的证明. 定理3的证明 假设该结论不成立,即argz=θ同时不是f(z)和g(z)的ρ(r)级Borel方向.根据定义1.4,分别存在三个判别的复数a1,a2,a3和b1,b2,b3和任意的ε0>0,使得 其中j=1,2,3.对于f(z)不失一般性,令a1=0,a2=1,a3=∞,否则只需要考虑 对于(3.1)式,对于充分大的r,有 即 注意到不等式 结合(3.3)式和(3.4)式,可以得出 运用引理2.2并结合(3.5)式,于是有 再运用精确级的定义,并结合(3.6)式可以得出 同理可得 由于h(z)=f(z)g(z),结合(3.7)式和(3.8)式所以得出 另一方面,根据引理3的结论,因为h(z)是复平面上无限级的亚纯函数,且射线L:argz=θ是函数h(z)的ρ(r)级Borel方向,所以得出 于是(3.9)式与(3.10)式矛盾,于是定理3得证. 推论1的证明 因为h(z)=f(z)g(z),将其变形为f(z)=h(z).因为argz=θ是f(z)但不是g(z)的ρ(r)级Borel方向,由定理3可得argz= θ是h(z)或者的一条ρ(r)级Borel方向.根据引理2.4得知,g(z)和具有相同的Borel方向,则argz=θ同样不是的ρ(r)级Borel方向.所以argz=θ必定是h(z)的一条ρ(r)级Borel方向.推论1完证. 推论2的证明 因为h(z)=f1(z)f2(z)···fn(z),将其变形为 因为argz=θ是fm(z)但不是fn(z)(n 6=m)的ρ(r)级Borel方向,由定理3可得argz=θ是h(z)或者(n 6=m)的一条ρ(r)级Borel方向.根据引理2.4得知,fn(z)和具有相同的Borel方向,则argz=θ同样不是的ρ(r)级Borel方向.所以argz=θ必是h(z)的一条ρ(r)级Borel方向.推论2完证. 推论3的证明 因为h(z)=f(z)+g(z),于是可以变形为h(z)=f(z)(1+).因为argz=θ是h(z)的一条ρ(r)级Borel方向,根据定理3的结论,于是有argz=θ一定是f(z)或者1+的ρ(r)级Borel方向.如果argz=θ是f(z)的ρ(r)级Borel方向,则推论3得证.如果argz=θ不是f(z)的ρ(r)级Borel方向,则一定是1+的 ρ(r)级Borel方向.根据引理2.5,则argz=θ一定是的ρ(r)级Borel方向.再次运用定理3的结论,则argz=θ一定是g(z)或者的ρ(r)级Borel方向.由于前面的假设,argz=θ不是f(z)的ρ(r)级Borel方向,则根据引理2.4可知,argz=θ也不是的ρ(r)级Borel方向.于是argz=θ一定是g(z)的ρ(r)级Borel方向.于是推论3完证. 推论 4 的证明 将h(z)=f1(z)+f2(z)+······+fn(z)变形为 根据定理3的结论,于是有argz=θ一定是f1(z)或者的ρ(r)级Borel方向.如果argz=θ是f1(z)的ρ(r)级Borel方向,则推论4得证.否则argz=θ一定是的ρ(r)级Borel方向.根据引理2.5,则argz=θ一定是的ρ(r)级Borel方向.将变形为 根据假设argz=θ不是f1(z)的ρ(r)级Borel方向,则利用引理2.4,argz=θ同样不是的ρ(r)级Borel方向,则argz=θ是f2(z)+f3(z)+···+fn(z)的ρ(r)级Borel方向.后半部分的证明类似前面,反复利用引理2.4、引理2.5和定理3的结论,并结合方程变形,则推论4完证. 定理1的证明 对于方程f00+A(z)f0+B(z)f=F(z),因为A(z)和B(z)都是有限级整函数,所以都没有ρ(r)级Borel方向.因为argz=θ是F(z)的ρ(r)级Borel方向,则根据推论4可得,argz=θ一定是f00(z)或者A(z)f0(z)或者B(z)f(z)的ρ(r)级Borel方向.现将定理证明分为3种情形. 情形1 如果argz=θ是f00(z)的ρ(r)级Borel方向,则根据引理2.6可得,argz=θ是f(z)的ρ(r)级Borel方向. 情形2 如果argz=θ是A(z)f0(z)的ρ(r)级Borel方向,则根据定理3的结论可得,argz= θ一定是A(z)或者f0(z)的ρ(r)级Borel方向.因为A(z)没有ρ(r)级Borel方向,所以argz=θ是f0(z)的ρ(r)级Borel方向,再根据引理6可得,argz=θ是f(z)的ρ(r)级Borel方向. 情形3 如果argz=θ是B(z)f(z)的ρ(r)级Borel方向,则根据定理3的结论可得,argz=θ一定是B(z)或者f(z)的ρ(r)级Borel方向.因为B(z)没有ρ(r)级Borel方向,所以argz=θ是f(z)的ρ(r)级Borel方向. 综上所述,非齐次项F(z)的ρ(r)级Borel方向一定是方程解f(z)的ρ(r)级Borel方向,则定理1完证. 定理2的证明设f(z)为方程f00+B(z)f=0的非平凡解,可以将方程变形为 类似文献[12],对(3.11)式运用Wiman-Valiron理论,于是得到 因此对于足够大的r,有 和 除去可能的一个有限测度集外成立. 由Dα,β(r,f)的定义,根据上述不等式可得 在除去可能的一个有限测度集外成立.因此,类似于上述的证明可得 在除去可能的一个有限测度集外成立.结合(3.11)式,有 另一方面,将方程f00+B(z)f=0变形为 则可以得到 结合定义1.2和引理2.1的(i)和上式可得 由于f的零点是单的,则 再由定义1.2、(3.14)式、(3.17)式和(3.18)式,考虑 和 根据引理2.1的(i)和(3.19)–(3.20)式,有 根据不等式 并且知道 结合定义1.4可得 即函数f(z)和f0(z)具有相同的精确级为ρ(r),于是结合(3.21)–(3.23)式以及定义1.4,则有 故有argz=θ是f的精确级零点聚值线当且仅当argz=θ是f0的精确级零点聚值线.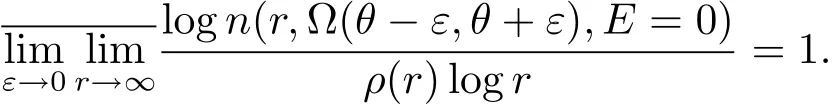
2 引理

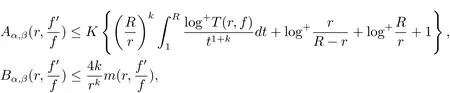
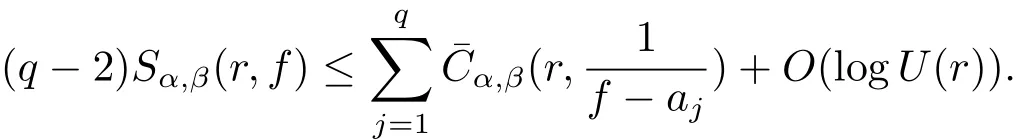

3 定理及推论证明