一种混合算法求解可分离带线性约束的变分不等式问题

张从军,李 赛,吕丽霞,王月虎

(1.南京财经大学应用数学学院,江苏南京 210023)

(2.南京财经大学管理科学与工程学院,江苏南京 210023)

1 引言

本文研究一类特殊的变分不等式问题:寻找一点u∗∈Ω,使得

其中u=(x,y)T,F(u)=(f(x),g(y))T,Ω={(x,y)|x∈X,y∈Y,Ax+By≥b}.将此类问题记作SMV I(Ω,F),这里X ⊆Rn和Y ⊆Rm为非空闭凸集,A∈Rl×n,B ∈Rl×m是矩阵,b∈Rl是向量,f:X→Rn,g:Y→Rm为单调映射,并且以上各量均已给定.因为映射f只取决于变量x,映射g只取决于变量y,所以被称为是可分离带线性约束的变分不等式问题.这类问题被广泛应用于研究网络分析、交通运输、图论等领域.目前对于问题SMV I(Ω,F)的研究,首先要在线性约束条件Ax+By=b中引入拉格朗日乘子λ∈Rl,进而得到原SMV I(Ω,F)的等价形式如下:求w∗∈Z,满足(w−w∗)TQ(w∗)≥ 0,w∈Z,其中w=(x,y,λ)T,Q(w)= ¡f(x)−ATλ,g(y)−BTλ,Ax+By −b¢T,Z=X × Y × Rl. 接着再对该等价形式进行求解.

交替方向法(ADM)是用来求解原问题SMV I(Ω,F)最经典的算法.一直以来,如何快速求解两个子变分不等式问题成了考查ADM有效性的关键,为此很多学者作了大量工作,对ADM 进行了相应的改进[1−5].虽然提出的各种改进策略在一定程度上有效提高了ADM的计算速度,但需要注意的是,此类改进的方法并没有完全避免求解子变分不等式问题.因为从计算角度上看,在大部分情况下,直接求解变分不等式并不是件容易的事情.为了能更好的提出新混合算法,接下来我们介绍对数二次临近点法.对数二次临近点算法(LQP)[6−11]主要用于求解如下这样一类变分不等式问题,即找一点u∗∈Ω,满足(u−u∗)TF(u∗)≥ 0,∀u ∈ Ω,其中这里矩阵A∈Rm×n,向量b∈Rm,Y为Rm中的闭凸子集,f:Rn→Rn是连续单调映射.LQP在每次迭代时只需解决这样一个非线性方程组

一般而言,求解一个非线性方程组比一个变分不等式组更容易操作.尽管此方法是对子问题进行非精确求解,但是相对于精确求解子问题,非精确求解更可行、快速.因为从数值计算角度分析,精确求解一个子问题往往不太容易实现.考虑到这个方法求解较容易的特点,LQP方法值得关注和借鉴.基于上面的考虑,本文提出了一种新的混合算法.此算法在预测步只需求解一系列相关联的非线性方程组,而不是去处理一系列的子变分不等式问题.同时这样做还可以在可行集中产生一个内点序列,在一定程度上提高了算法的有效性和可行性:在修正步中,修正值是由当前预测点和一个投影算子构成的凸组合得到的.这样保证了如果前一个迭代点是内点,那么这样一个凸组合得到的下一个迭代点也将会是内点.另一方面需要注意的是,当可行集为简单集时,投影算子更容易执行.

本文结构如下:第2节主要概述了本文所需要的预备知识,参见文献[12–15];第3节在映射单调和原变分不等式解集非空的条件下提出一种新的混合算法,并给出算法的一些性质,相关证明技巧参见文献[16–21];第4节和第5节分析了新算法的收缩性及全局收敛性,参见文献[22–26];第6节利用数值算例验证了算法的有效性.

2 预备知识

令PΩ(·)为Rn到Ω上的投影映射,即PΩ(x)=argmin{ky−xk|y∈Ω}.投影映射有如下重要性质.

引理1[6]若Ω⊆Rn为一非空闭凸子集,PΩ(·)为Rn到Ω上的投影映射,对于任意的x,y∈Rn,任意z∈Ω,有

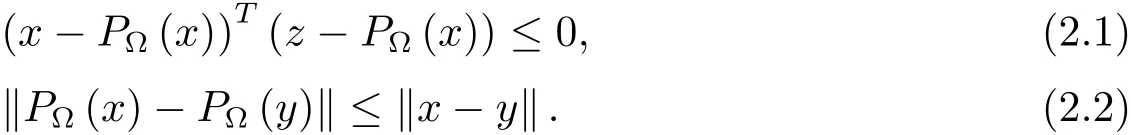
定义1集合Ω⊆Rn,设f是Ω→Rn的映射,如果f满足(x−y)T(f(x)−f(y))≥0,∀x,y∈Ω,则称f在Ω上是单调的.若不等号严格成立,则称f在Ω上是严格单调的.

3 算法的设计和性质

以下给出新的LQP-ADM[11−24]混合算法用于求解可分离带线性约束的变分不等式问题的步骤,然后给出此算法的一些性质.算法的步骤如下.

步0 令 ε>0,µ1,µ2∈(0,1),t∈(0,1),k=0,w0=(x0,y0,λ0)∈X ×Y ×Rl,H 为一给定的l×l阶对称正定矩阵,X ⊆Rn和Y⊆Rm为非空闭凸集,A∈Rl×n,B∈Rl×m是矩阵,b∈Rl是向量,f:X→Rn,g:Y→Rn为单调映射.

下面的符号类似.

步1.3

步3计算步长

观察新算法的预测步可知,此算法的主要任务是解下面两个非线性方程的近似解:带入点 ¡xk,yk,λk¢求解 x,

带入点 ¡xk+1,yk,λk¢求解 y,

比较(3.5),(3.6)两式的共同点就相当于求解如下方程的近似解

其中 uk=(m1,m2,···,mn),u=(w1,w2,···,wn),

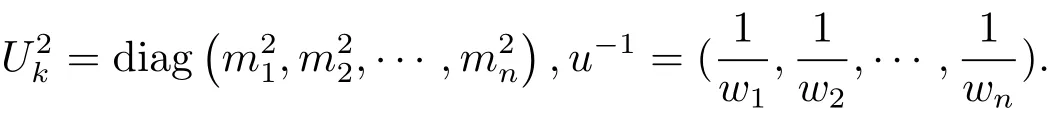
引理2[6]如果q(u)为Rn上的单调映射,则对于给定的uk∈,方程(3.7)存在唯一的u∈.

因为(x),g(y)分别是关于x和y的单调映射,所以由此性质可知非线性方程(3.5)和(3.6)都有唯一的解.

则对任意v≥0,有下面不等式成立:

其中

证 令v=(vx,vy,vλ),则(3.8)式证明包括下面三个不等式的证明:

不失一般性,可以将不等式(3.10)中的x,xk,qx,vx简化为实数.因为x>0,xk>0,vx>0,故有.结合方程组(3.8)有

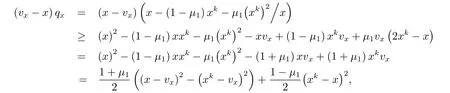
则(3.10)式得证.同理可证得(3.11)式也是成立的.下面来证明(3.12)式,由方程组(3.8)可得则(3.12)式得证.综上所述,要证的不等式成立.证毕.

下面给出一个引理来解释算法中的停机准则.

同理可得

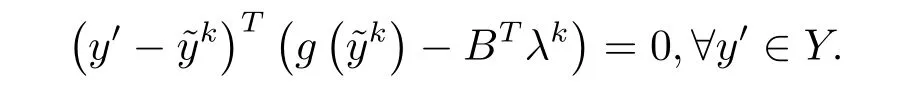
4 算法的收缩性

本节准备给出任取w∗=(x∗,y∗,λ∗)∈W∗,由上面的LQP-ADM 混合算法得到的序列满足

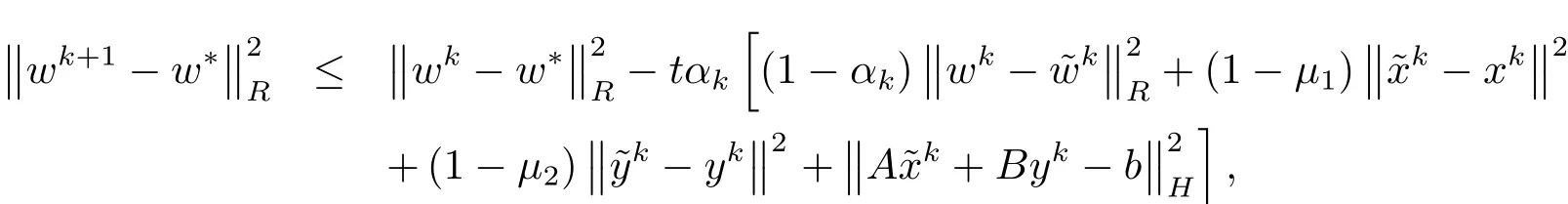
我们先来探讨提出的LQP-ADM混合算法的预测步.

证 因为 w∗=(x∗,y∗,λ∗)是 SMV I(Ω,F)的解,所以

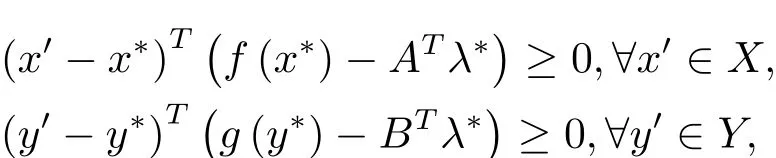
以及Ax∗+By∗=b在上面的两个不等式中,分别令,则

另一方面,因为(3.5)式及下面的恒等变形

所以根据引理3可得

将(4.2)式与(4.4)式相加

又因为f(x)是单调映射,则

即

同样由(3.2)式及引理3可得

将(4.3)与(4.6)式相加有

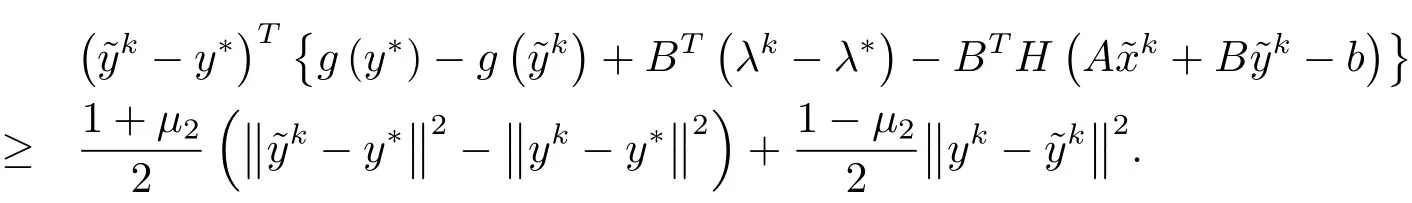
又因为g是关于y单调的,则

则

将(4.5)与(4.7)式相加有

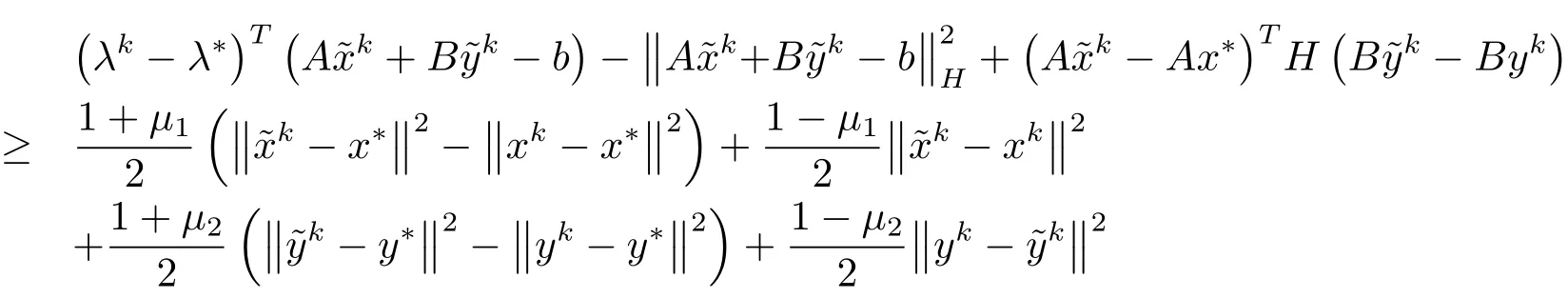
得证.

于是如果考虑(4.8)式,则可得到如下引理.

证 将(4.8)式代入引理5中有

即

证毕.

由上面的引理可得到关于LQP-ADM混合算法预测步的定理如下.

其中

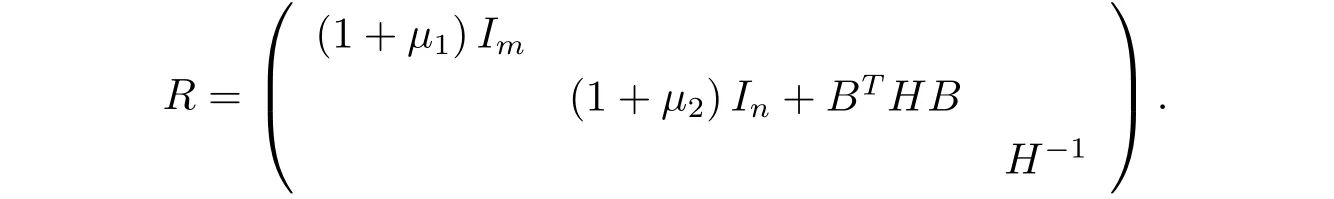
证 由引理6可知

同时有

将(4.9)式与此恒等式相加可得

于是

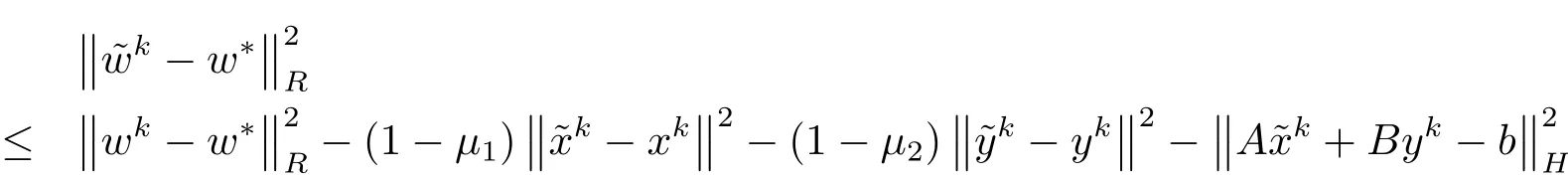
得证.

将定理1的结论作简单变形可得到以下推论.

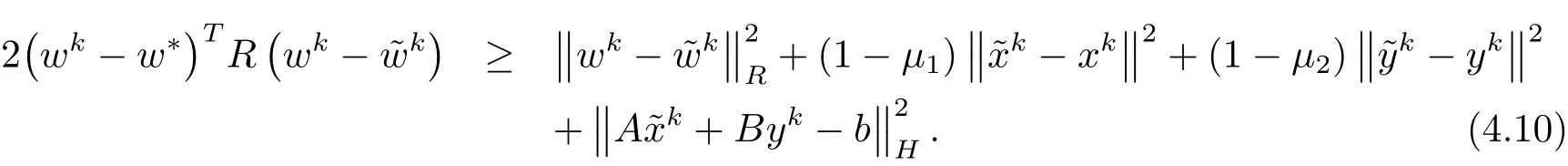
证 由定理1可得

于是

得证.

基于以上对混合算法中预测步的讨论,结合算法的修正步可得到算法的收缩性定理如下.

证 由式(3.4)得到

利用柯西-施瓦茨不等式和投影的非扩张性,可推出

再结合推论1可得

得证.

5 算法的收敛性

在证明算法的全局收敛性之前,先给出一个重要的引理.

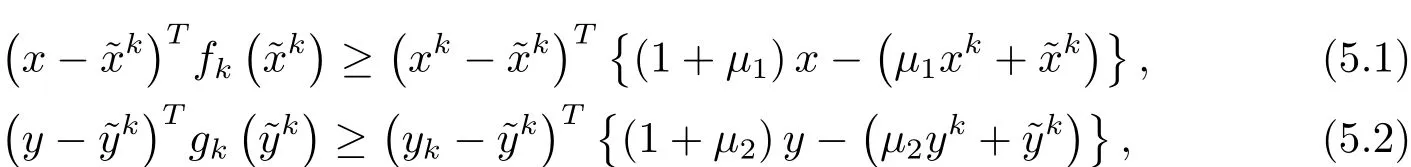
其中

将此不等式右端变形为

基于对LQP-ADM混合算法收缩性的讨论,接下来给出此算法的全局收敛性分析.

证 此定理可以分两步来证:首先利用已经得到的结论证明w∞是SMV I(Ω,F)的解,然后再证明序列'“收敛于w∞.

步1由定理2可得

因为 µ1,µ2,t∈ (0,1),所以

由(5.5)式可知必定存在常数c>0,使得

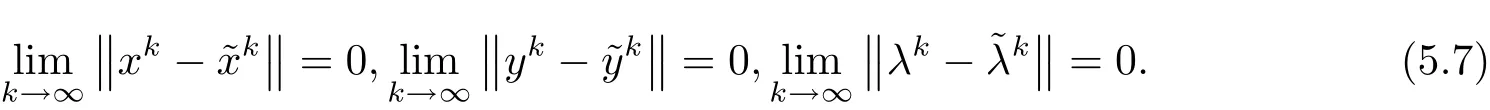
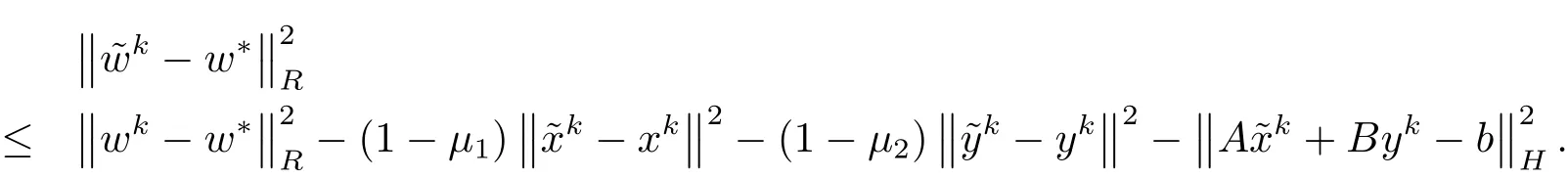
进而有

故

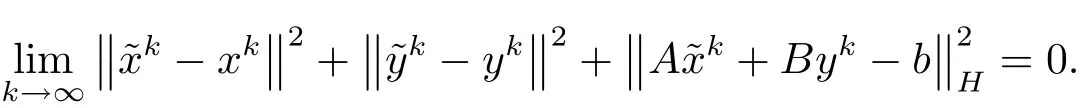
于是

结合(5.3)式和(5.4)式可得

则

进而由(5.1),(5.2)及(5.7)式可得

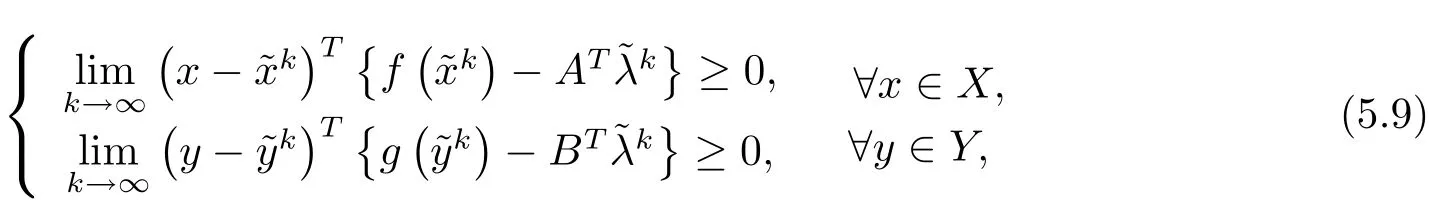
令w∞为的一个聚点且其中一个子列'“收敛于w∞.则由(5.7)及(5.8)式可得

因此

即(w−w∞)TQ(w∞)≥0,∀w∈Z,这说明w∞是SMV I(Ω,F)的解.

步2对于SMV I(Ω,F)的所有解都满足不等式(5.6),所以可推出

所以∀k≥l,由(5.11)式可得

6 数值实验

为了考察LQP-ADM混合算法的数值表现,用Matlab软件编程来进行数值实验,所有程序在Windows 2007系统下进行.考虑这样一个优化问题,其中

为了保证问题的可行性,kbk≤r1+r2必须满足.比如选取r1=0.5kbk,r2=0.6kbk.

引入辅助变量y,则上述问题转化后的形式如下:

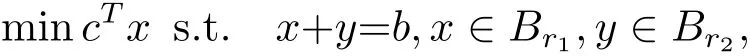
其中Br表示圆心为原点、半径为r的圆.

接着将上述凸规划问题转化为可分离带线性约束的变分不等式问题,即找一点u∗∈Ω,满足,其中

由于向量c与向量b的元素均是随机产生的,所以每次运行LQP-ADM混合算法求得变分不等式的解都不相同,但是解均是收敛的并且收敛性态是一致的.为了说明情况,从多次运行结果中选取下面三组图――图1、图2与图3来分析.从这三组图可知,x与λ的收敛趋势是一样的,都是随着迭代次数的增加其中一个分量增大另一分量减小,但是y的收敛趋势却不同,图1中y的两个分量随着不断迭代都是增大的,图2中都是减小的,而图3中却是一个增大另一个减小,同时容易看出新算法的收敛速度很快,所以LQP-ADM混合算法求解问题SMV I(Ω,F)的解是收敛的,也是有效的.

图1:所求点的收敛曲线1

图2:所求点的收敛曲线2

图3:所求点的收敛曲线3